基于深度学习的汽车梁类件冲压回弹研究

聂昕 谭天 申丹凤

摘要：提出了基于深度学习的汽车梁类零件回弹预测方法。基于二维回弹理论，将三维梁类零件离散为若干截面，采用双平面投影法和图像二值化方法，将梁类零件的截面曲线转换为神经网络模型可识别的双通道图像数据。基于拉丁超立方采样法对影响梁结构零件的冲压工艺参数及板料材料参数变量进行采样，通过CAE回弹仿真得到后续深度学习网络的训练样本。为研究梁结构在不同几何截面、材料参数、工艺参数作用下的回弹问题，采用基于LeNet-5、AlexNet、NiN的卷积神经网络模型作为几何截面识别模型，同时使用全连接神经网络模型耦合材料参数和工艺参数的方法，得到该梁类零件回弹算法模型。以某汽车梁类结构零件作为研究对象，基于高斯混合聚类将回弹样本分为小回弹、中等回弹、大回弹三个类型。将各类回弹样本分别通过回弹算法模型进行验证，结果表明，基于AlexNet的模型准确度最高，同时算法鲁棒性相较于其他两种也更强，更适合梁类件的回弹预测。

关键詞：梁类零件；冲压回弹；深度学习；拉丁超立方采样；高斯混合聚类

中图分类号：TG156;U466

DOI：10.3969/j.issn.1004132X.2023.07.010

Research on Stamping Springback of Automobile Beam Parts Based on

Deep Learning

NIE Xin1 TAN Tian1 SHEN Danfeng2

1.State Key Laboratory of Advanced Design and Manufacturing for Vehicle Body，Hunan University，

Changsha，410082

2.AISN Auto R＆D Co.，Ltd.，Changsha，410205

Abstract： A method was proposed herein for springback prediction of automobile beam parts based on deep learning. Based on the two-dimensional springback theory， the three-dimensional beam parts were discretized into several sections， and the cross-section curve of the beam parts was converted into a dual-channel image that could be recognized by neural network model using the method of double-plane projection and the image binarization method. Based on Latin hypercube sampling method， the stamping process parameters and sheet material parameters of the beam structure parts were sampled， and the subsequent deep learning network training samples were obtained by CAE springback simulation. In order to study the springback of beam structures under different geometric cross-sections， material parameters， and processing parameters， convolutional neural network models based on LeNet-5， AlexNet and NiN were used as geometric cross-section recognition models. Meanwhile， the fully connected neural network model was used to couple material parameters and processing parameters to obtain the springback algorithm model of beam parts. Car beam structural parts were taken as the research object. Based on Gaussian mixture clustering， the springback samples were divided into three types： small springback， medium springback， and large springback. Each type of springback sample was verified by the springback algorithm model. Verification results show that the deep learning model has the highest accuracy based on AlexNet， and the algorithms robustness is also stronger than that of the other two， which is more suitable for springback prediction of beam parts.

Key words： beam part; stamping springback; deep learning; Latin hypercube sampling; Gaussian mixture clustering

0 引言

梁类零件是承载式车身零件中最重要的结构件之一，它的存在保证了白车身的承载能力，以及车身自身的刚度，该类零件具有特殊的性能要求和受载能力要求，通常选用高强钢作为生产制造的材料。这些梁类零件跨越车身的几大总成，同时和其他零部件具有焊接或装配关系，因此，汽车梁类结构零件的生产精度是否满足要求直接关系到后续生产环节的顺利进行。目前国内外汽车行业正在开展“2 mm”工程，即保证整车在装配环节的整体误差在2 mm以内，这也表明对汽车零部件的制造精度有严格要求。

近年来，许多学者对金属板料冲压回弹进行了深入研究，其中，基于二维截面法的梁类零件冲压回弹研究是一种常见的分析方法。聂昕等［1-2］通过与实际沖压件的对比表明使用二维截面法对冲压零件进行回弹预测具有较好的效果。刘迪辉等［3］通过截面法对不同形状的二维截面曲线回弹进行理论研究，并通过一B柱零件验证理论的正确性，结果表明利用二维截面法简化三维零件的回弹，能够保证最终结果的精度［4］。然而，使用二维截面法很难准确预测形状变化复杂的三维零件。

对于形状变化复杂的三维零件，目前国内外学者大多集中在采用有限单元法对零件进行成形过程模拟进而分析回弹量大小。高志国等［5］以700 MPa高强钢钢带为研究对象，使用CAE仿真研究了多种参数下钢带冲压成形的回弹大小，并基于响应面法得到相应参数和回弹的函数模型，最终通过寻优算法得到回弹最小的成形工艺参数。张旭等［6］以高强钢防撞梁为研究对象，通过Dynaform有限元软件研究该零件由热冲压改为冷冲压的成形过程，通过优化冲压工艺参数，使零件顺利冲压成形，且减小成形后的回弹。黄仁勇［7］基于有限元模型研究扭曲回弹机理，采用Voce-Chaboche混合硬化模型分析双C梁的扭曲回弹，结合响应面法和蚁群算法得到优化参数，减小双C梁的扭曲回弹。以上研究虽然在金属薄板冲压回弹领域取得了不错的研究成果，但是侧重点主要集中在简单截面曲线、工艺参数及材料参数的某个方面上。现实生产中，梁类结构零件往往有复杂的几何形状、多种类的材料类型以及多变的工艺参数，使用CAE仿真方法对梁类结构零件进行回弹分析预测，存在参数设置复杂、使用门槛较高、计算时间长、计算轮次多等问题，极大延长了企业的生产周期。

人工智能方法具有运算速度快、处理数据能力强、模型设置简单等优点。部分学者采用人工智能网络来研究汽车零件的成形回弹等问题。CRINA［8］以一圆筒为研究对象，以拉深工序中的工艺参数为输入变量，产品的最终回弹为输出变量，经样本训练后建立相应的人工神经网络，并通过优化相应的工艺参数，成功减小了产品的回弹。 HAMBLI等［9］将有限元冲压成形模拟技术与人工神经网络技术相结合，研究板材冲压时的模具间隙与成形后的材料延伸率之间的函数关系。龙仕彰［10］基于有限元冲压模拟技术，结合人工神经网络模型，研究冲压工艺参数对盒形件冲压成形回弹的影响，并通过遗传算法优化冲压工艺参数，减小了盒形件的回弹。张玉平［11］通过正交试验方法和CAE仿真获得的试验样本，基于BP（back propagation） 网络建立了U形件弯曲回弹预测系统，并通过附加试验验证预测系统的准确性。不同工艺参数值在有限的取值区间内是规律的连续变量，由于设计和材料制备的原因，零件的形状和材料属性参数取值空间大、难控制、无规律、离散变量多、需求样本多，因此，以上使用人工神经网络模型的研究更侧重于研究不同工艺参数下的回弹，而未考虑零件实际的几何形状和材料属性。

为更准确地研究几何形状因素、材料属性因素、工艺参数对梁结构零件回弹的综合影响，本文在上述研究的基础上提出了基于深度学习的梁类结构回弹算法模型，应用于汽车梁结构零件的回弹分析。

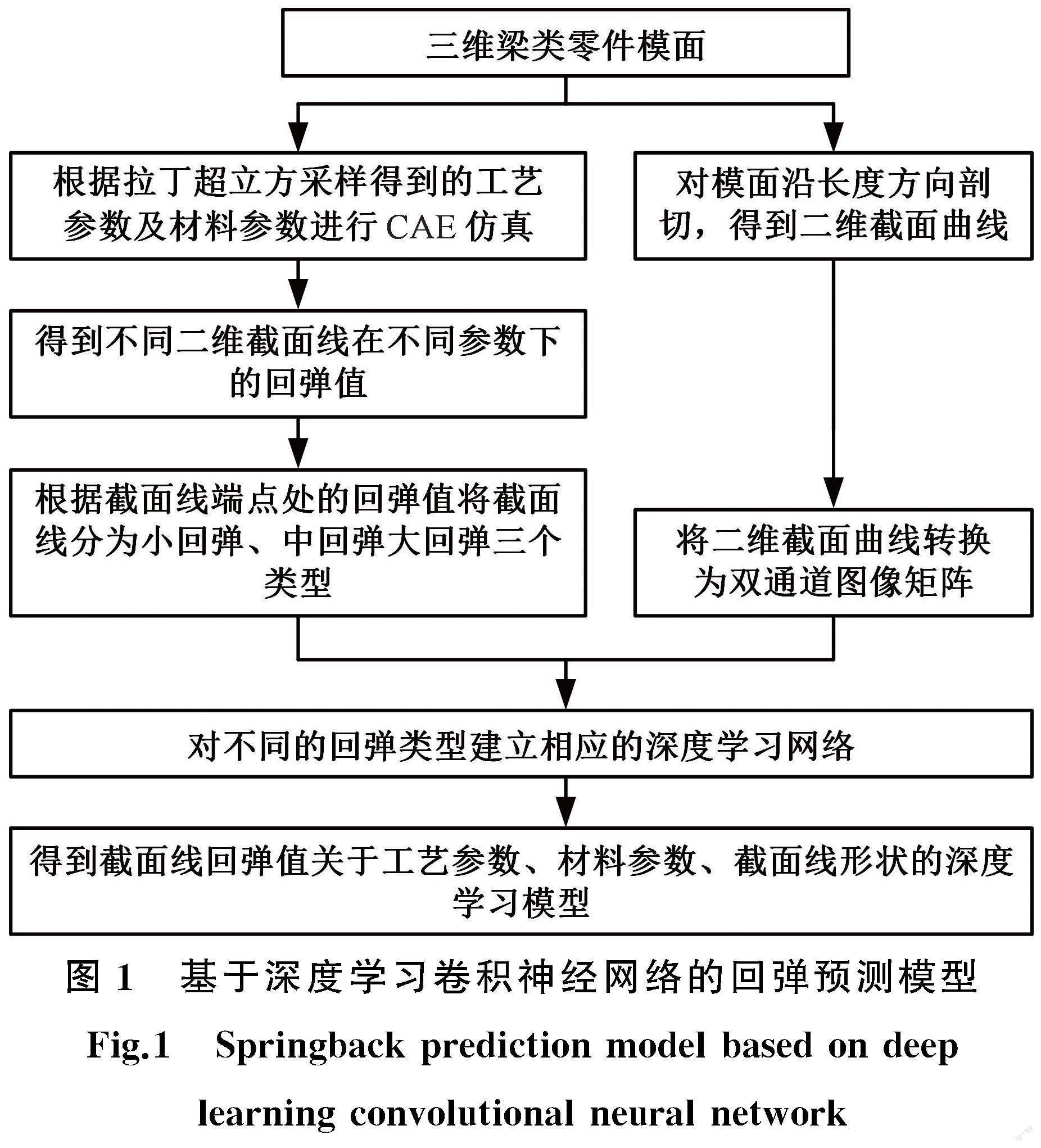
其中，二维截面法是指将三维梁类零件离散为若干特征截面，将离散得到的特征截面曲线拉伸成“几”字形的简单二维形状，再通过LS-DYNA等有限元仿真软件对拉伸得到的简单几何形状零件进行相应的冲压仿真及回弹计算，通过仿真结果判断离散特征截面的实际回弹。

本文在二维截面法的基础上，通过深度学习图像识别技术，研究零件截面线在不同参数下的回弹情况。采用人工智能与二维截面法研究三维零件的回弹，首先需要将二维截面线转变为人工智能网络可识别的信息。为此，将梁类零件二维截面线分别在俯视平面、左视平面上投影并将投影曲线转化为数值矩阵，形成一种既能反映二维截面曲线形状特征，又包含空间位置信息，并能被深度学习等人工智能网络识别的二维截面离散数值转化方法。

使用二值化模型，可以方便快捷地将曲线转化为计算机可识别的图像矩阵。首先在投影平面上划分若干栅格，然后将曲线向其投影，将投影曲线内的栅格数值置为1，其余置为0，如图2所示，就能将平面二维曲线转化为图像信息。

使用二值化模型对三维空间曲线进行转化，将梁类零件沿其长度方向分布若干点；以每个点为基点，该点在边长曲线上的法平面为剖切平面，对该零件进行剖切，得到相应的截面曲线；对截面曲线分别在左视平面、俯视平面上投影，得到两条投影曲线；对投影曲线进行二值化转化，得到双通道图像矩阵。

2 回弹预测算法模型

该深度学习网络模型主要由两部分组成，第一部分通过卷积神经网络实现对输入的双通道图像矩阵进行特征提取，得到一组抽象的几何特征向量；第二部分是一个全连接神经网络模型，将第一部分得到的几何特征向量与工艺参数、高强钢材料参数结合，预测出相应截面线处回弹大小。

在该模型中，首先基于二维回弹理论，将梁类结构零件划分为若干截面，做出相应的截面特征线，然后使用曲线二值化的方法，得到网络模型需要的双通道图像数据，分别经LeNet-5、AlexNet、NiN卷积神经网络［12］进行图像数据特征提取后，将得到的数据特征向量与影响回弹的冲压工艺参数及材料本身的材料参数通过全连接神经网络结构耦合，最终得到不同截面线形状在多种工艺条件和不同材料类型下的回弹预测模型。

2.1 基于AlexNet的卷积神经网络结构

传统AlexNet网络采用三通道输入来处理RGB类型图片数据，调整架构后使其适用于双通道图片输入，增加卷积层数，增强对较大图像的处理能力，同时去掉网络末端用于解决分类问题的reducemean层和softmax层，直接使用神经元作为下层用于回弹回归预测的全连接神经网络输入端，修改后的AlexNet网络架构如表1所示。

该部分网络的主体结构为5个卷积层和2个全连接层。这是由于输入的双通道图像是较为简单的曲线图像，图像所包含的信息比其他类型的图片少，因此在原AlexNet网络模型的基础上减小了模型规模，既能防止模型的过拟合，又减少了模型所含参数，降低存储空间的要求，加快模型训练速度。同时，考虑对截面回弹影响较大的曲线圆角半径，选用较小的卷积核，防止由于卷积核的感受野太大而造成的信息丢失。在每个网络层后均添加Dropout层并使用L2正则化方法降低整个模型的过拟合问题。保留全连接层的152个神经元，构成最终的图像特征向量。

2.2 基于LeNet-5的卷积神经网络结构

传统LeNet-5网络采用三通道输入来处理RGB类型图片数据，调整架构后，该网络在原始LeNet-5的网络模型基础上保持主要的结构构型不变，使用较小的卷积核以便卷积层能更好地观察到曲线图像的细节，同时使用Dropout层防止网络的过拟合现象，去掉了原LeNet-5网络中的softmax层，并将原模型中的激活函数更换为ReLu［13］激活函数，提高计算效率，加速模型训练，同时避免原激活函数“梯度弥散”等问题，保留了全连接层的152个神经元，构成最终的图像特征向量。调整过的LeNet-5网络结构如表2所示。

与AlexNet网络相比，LeNet-5网络的卷积核运算操作相似，使用了相同的激活函数对网络模型进行非线性化，不同之处在于AlexNet网络比LeNet-5网络层数更深、模型更大。

2.3 基于NiN的卷积神经网络结构

与上文处理方式类似，将NiN卷积神经网络结构的输入通道改为双通道图像输入并调整参数。优化后的网络结构参数如表3所示。

优化后的网络使用了更小卷积核以便保留曲线的细节信息；去掉了一层MLP结构，这是因为网络所学习的图片信息相较于原始网络信息量更小，去掉一层网络结构更有利于网络的训练，同时能避免过拟合；加深了卷积层的深度，提高网络提取图像信息的维度，提高网络的精度。

2.4 网络结构

ReLu函数的数学表达式为

f（x）=max（0，x）（1）

通过分析ReLu函数在定义域内的导数可以发现，当输入值x∈［-∞，0］时，导数恒为0;当输入值x∈［0，+∞］时，该函数的导数大于零。因此该激活函数求导形式简单，并且激活区域内的导数值不随网络的深度变化而变小，解决了深度学习中的“梯度消失”问题。

Adam优化算法使用梯度的一阶矩估计和二阶矩估计对深度网络模型中的每个参数的学习率均进行优化修正［15］，該算法深度学习网络中相应的权重系数迭代修正方式如下：

式中，gt为网络损失函数的一阶梯度值;mt为梯度在动量形式下的一阶矩估计;vt为梯度在动量形式下的二阶矩估计;m^t为偏差纠正后的一阶矩阵估计;v^t为偏差纠正后的二阶矩估计;η为模型学习率;ωt为第t轮迭代时神经网络中的待学习参数;β1、β2分别为一阶矩估计的衰减率和二阶矩估计的衰减率;ε为小常数，防止式（6）分母为0。

L2正则化数学表达式如下：

式中，W为对应的网络层权重系数参数;λ为正则化系数，通过控制λ的大小控制整个模型的复杂度。

Dropout正则化又称为随机失活法 ［16］，令神经网络中的每个神经元都以概率P处于抑制状态，在测试阶段使得每个神经元都处于激活状态，同时乘以权重1-P以保持模型在训练阶段和测试阶段有相同的权重。

2.5 自定义损失函数

损失函数用于定量地区分模型的估计输出（预测）与正确输出（真实标注）之间的差异，本文问题属于回归预测类型，选用绝对值损失函数，定义如下：

式中，j∈［1，N］;yj表示训练样本的真实结果;pj表示模型的预测结果;N为样本数量。

截面线上不同位置的回弹程度不同，为使模型的输出结果更符合截面线回弹的分布规律，提高模型的训练效率，在选用绝对值损失函数的基础上，对每个点的结果添加不同的权重系数，使模型的输出结果更符合样本数据的分布。该损失函数的形式如下：

式中，pk，j、yk，j分别为单个样本点回弹的预测值和真实值;m为输出结果的维度，本文中m=10；αk为相应的权重系数。

由于本文研究的梁结构截面曲线两端回弹大、中间回弹小，并且两者相差较大，所以在设置权重系数αk时，通过加大截面线中间点的权重系数以提高模型对截面线中间点的训练精度，使模型输出结果更贴合实际结果。

2.6 全连接回弹预测结构

全连接层神经网络主要负责对上一级卷积神经网络得到的特征向量与样本工艺参数及样本材料参数进行耦合，层与层之间采用全连接方式进行连接。该网络主要包括输入层、隐藏层和输出层。输入层为卷积神经网络的输出和样本参数，输出层为对二维截面线的10个参考点回弹量的预测值。采用正则化等方法降低数据过拟合问题。全连接层的神经网络结构如图3所示。

在图3中，A1，A2，…，A152为上层卷积神经网络最终得到的152个图像特征向量，B1，B2，…，B8为8个样本工艺参数及样本材料参数，Y1，Y2，…，Y10为10个参考点的回弹量大小。具体的网络结构如表4所示。

该部分的主体结构由输入层、两层中间层以及输出层构成，在全连接层FC_3和全连接层FC_4

后均添加了Dropout层以及使用L2正则化方法降低模型过拟合发生的风险。最终输出的10个点为截面曲线上10个参考点的回弹值大小。

3 仿真验证及训练

3.1 基于拉丁超立方采样的回弹仿真样本

以某汽车大梁为研究对象，调研文献［17-19］，本次试验设计的变量见表5，设定采样样本数目为400。

对典型的类U形梁类零件进行仿真。梁上有吸收冲压时纵梁高度过度区域内的吸皱凹坑，防止零件在冲压时材料堆积引发起皱问题；在梁的左部区域有用于安装定位的装配孔，这段区域内的梁结构呈凸起形状。结构如图4所示，在Dynaform中根据采样结果设置相关仿真参数，提交求解器运算，CAE网格模型如图5所示。

3.2 三类回弹类型样本建立

对梁类零件而言，截面线端点处的回弹值最大也最值得关注。为提高后续神经网络的拟合效果，将每根曲线的回弹最大值即端点处（点1和点10）的回弹值作为特征值，进行高斯混合聚类，设置为3个混合模型，分类结果如图7、图8所示。

由图7、图8可知，采用高斯混合聚类方法将该零件回弹分为小回弹、中等回弹、大回弹三类，总体结果如表6所示。

以下将对三类样本分别建立神经网络模型，进行拟合训练。其中小回弹、中等回弹、大回弹分别取500、600、300个样本作为验证集合。

4 回弹算法模型结果分析

4.1 基于三种卷积神经网络模型的算法实验结果与分析

从图9～图11中可以看出，训练后的三种神经网络模型对各个回弹类型的数据的拟合能力不同。三种模型训练在总体上有以下特点：

（1）样本误差比样本模型误差小。原因是样

本模型误差中还包含了网络的正则化误差等模型误差，因此样本误差会比样本模型误差低一个“常数”误差。

（2）每种网络模型中均是小回弹类型误差最小，中等回弹类型误差次之，大回弹类型的样本误差最大。小回弹和中等回弹样本中，训练的神经网络能较好地拟合样本的回弹数值，总体上能反映回弹情况，且包含的训练样本个数较多，网络模型能经过充分的样本训练，故其精度较高；而大回弹类型的大误差样本误差相对较大，网络的拟合结果较差，主要原因是极端样本的识别分辨能力较弱，同时数据样本量较少，导致模型对该类型数据训练量不够，导致该模型对此类数据的拟合能力较弱。

4.2 模型性能比较

对比不同网络模型和不同回弹类型的样本模型误差平均值和标准差，性能指标如图12所示。

由图12可知，大回弹样本中基于LeNet-5、AlexNet和NiN卷积神经网络模型的回弹误差平均值分别为0.92 mm、0.70 mm、0.83 mm，大部分回弹数值在5 mm以上，因此模型误差基本能保证在20%以内。在中等回弹样本中，三类模型的误差平均值分别为0.50 mm、0.31 mm、0.42 mm，回弹数值集中在2～5 mm区域中，模型误差也能控制在20%左右。在小回弹样本中，三类模型的误差平均值分别为0.20 mm、0.12 mm、0.18 mm，回弹数值集中在0～3 mm区域中。

从图12中可以看出，基于AlexNet卷积神经网络模型的回弹预测算法效果最好，准确率最高。从结构上分析，基于AlexNet的模型深度最大，结构也最为复杂，而基于LeNet-5的模型最简单，模型参数最少，因此该模型的性能最差。从误差标准差上来看，每类回弹样本的三种模型下的误差标准差最大为0.46 mm，最小为0.058 mm，表明每个模型均较好地拟合了回弹数据，同时三类回弹样本中，大回弹样本的误差标准差最大，这是由于大回弹样本数据最少，模型训练不足；训练样本数量最多的小回弹样本的误差标准差就较小，这也表明模型的泛化能力更好。

4.3 基于AlexNet的模型训练结果误差分析

分析上文效果最好的基于AlexNet的模型训练结果，在小回弹、中等回弹、大回弹中取出数据分析，分别取误差最小、最接近平均误差、误差最大的3个样本进行分析比较。

分析误差较大的样本，其中小回弹取平均误差大于0.18 mm，共计56个样本；中等回弹误差取大于0.60 mm，共计38个样本；取大回弹类型中误差较大的样本分析，大回弹取平均误差大于1.00 mm，共计50个样本。取每个样本的点1（截面线端点处）作y轴，点10（截面线端点处）作x轴，作出回弹分布，结果如图13所示。

由图13a可知，大误差样本较为均匀地分布在整个点集中，这表明小回弹样本产生较大误差的主要原因是对应网络的拟合能力不足，并且由于小回弹样本中各点的回弹数值本身太小，在网络进行梯度优化时，整个网络难以到达最优参数，导致大误差样本的均匀分布。

由图13b可知，大误差样本主要分布在两个部分：一是点集的边缘，二是样本密度较小的位置。处在边缘的样本表明网络对边缘处的分辨能力较弱，实际上这是网络对“极端样本”的拟合能力不够，而处于样本密度较小的位置则是由于该处的样本数量不足，从而导致网络在该样本处的预测结果误差较大。

由图13c可知，除极个别大误差样本分布在数据密度較小处外，绝大多数大误差样本集中在中等回弹样本和大回弹样本的交界地带，这也代表该模型对处于“边缘地带”的极端样本的分辨能力较弱，同时这些类型的数据在整个训练数据中数量较少，训练量不够。以上原因导致了该模型对此类数据的拟合能力较弱。

5 结论

（1）本文通过深度学习，引入了提取几何特征的复杂形体特征及准离散材料参数作为参数变量的卷积神经网络，对汽车梁类结构零件冲压回弹进行了较好的预测。

（2）本文提出了一种截面曲线图像化方法，将截面曲线在两个栅格平面上投影，采用二值化方法形成了双通道的图像矩阵，以便后续神经网络模型的学习训练。

（3）基于LeNet-5、AlexNet、NiN卷积神经网络模型研究该汽车梁零件在不同工艺参数及不同材料参数下的回弹情况。结果表明，AlexNet卷积神经网络模型的拟合性能最好，准确度最高，并且该模型对三种回弹类型有较好的预测能力，对中等回弹和大回弹两种回弹类型都能较好拟合。

下一步研究可考虑其他神经网络模型的识别能力，以及其他形式的卷积核能否提高模型的训练速度和精度；冲压时端头封闭的梁类零件的回弹问题;将截面曲线处理为视频格式，使用3D卷积处理，加深梁截面曲线间的连续性，基于大数据建立梁结构的回弹预测系统;使用三维数据结构，预测参考点在x，y，z方向上的回弹数值，使用回弹补偿算法对模面进行优化。

参考文献：

［1］ 聂昕，成艾国，钟志华，等. 二维截面法在精确预测汽车梁类件回弹上的应用［J］.汽车工程，2007（1）：83-86.

NIE Xin， CHENG Aiguo， ZHONG Zhihua， et al. Application of Two-dimensional Cross-section Method in Accurately Predicting Springback of Automobile Beam Parts［J］.Automotive Engineering， 2007（1）：83-86.

［2］ 聂昕，申丹凤. 高强度梁类件回弹及补偿的二维截面法修正［J］.中国机械工程，2013，24（2）：180-185.

NIE Xin， SHEN Danfeng. Two-dimensional Section Method for Springback and Compensation of High Strength Beam Parts［J］. China Mechanical Engineering， 2013，24（2）：180-185.

［3］ 刘迪辉，吴磊，李光耀，等. 任意截面线回弹理论计算方法及应用［J］.锻压技术，2009，34（6）：143-147.

LIU Dihui， WU Lei， LI Guangyao， et al. Calculation Method and Application of Springback Theory for Arbitrary Section Line［J］. Forging ＆ Stamping Technology， 2009，34（6）：143-147.

［4］ 吴磊，李光耀，曹昭展. 基于截面法的冲压回弹特征评价方法［J］.中国机械工程，2009，20（19）：2280-2283.

WU Lei， LI Guangyao， CAO Zhaozhan. Evaluation Method of Stamping Springback Characteristics Based on Section Method［J］. China Mechanical Engineering， 2009，20（19） ： 2280-2283.

［5］ 高志国，徐流杰. 基于响应面法的700 MPa高强度低合金钢带冷冲压回弹分析［J］. 热加工工艺，2018，47（17）：147-150.

GAO Zhiguo， XU Liujie. Cold Stamping Springback Analysis of 700 MPa High Strength Low Alloy Steel Strip Based on Response Surface Method［J］.Hot Working Technology， 2018，47（17）：147-150.

［6］ 张旭，周杰. 超高强度钢防撞梁热成形改冷冲压工艺设计及优化［J］. 重庆大学学报，2011，34（1）：77-81.

ZHANG Xu， ZHOU Jie. Process Design and Optimization of Hot Forming to Cold Stamping for Ultra-high Strength Steel Anti-collision Beam［J］. Journal of Chongqing University， 2011，34（1）：77-81.

［7］ 黄仁勇. 高强钢冲压成形过程中的扭曲回弹及补偿研究［D］. 成都：西南交通大学，2018.

HUANG Renyong. Research on Distortion Springback and Compensation in Stamping Process of High Strength Steel［D］. Chengdu：Southwest Jiaotong University， 2018.

［8］ CRINA A. Control the Springback of Metal Sheets by Using an Artificial Neural Network［J］. AIP Conference Proceedings， 2007，907（1）：235-238.

［9］ HAMBLI R， GUERIN F. Application of a Neural Network for Optimum Clearance Prediction in Sheet Metal Blanking Processes［J］. Finite Elements in Analysis & Design， 2003，39（11）：1039-1052.

［10］ 龍仕彰. 基于人工智能的冲压件复合参数数值优化技术研究与应用［D］.杭州：浙江大学，2007.

LONG Shizhang. Research and Application of Numerical Optimization Technology of Composite Parameters of Stamping Parts Based on Artificial Intelligence ［D］.Hangzhou： Zhejiang University， 2007.

［11］ 张玉平. 基于人工神经网络U形件回弹预测的研究［D］. 重庆：重庆大学，2007.

ZHANG Yuping. Research on Springback Prediction of U-shaped Parts Based on Artificial Neural Network ［D］. Chongqing： Chongqing University， 2007.

［12］ JAREMENKO C， RAVIKUMAR N， AFFRONTI E， et al. Determination of Forming Limits in Sheet Metal Forming Using Deep Learning［J］. Materials （Basel， Switzerland）， 2019，12（7）：1051-1064.

［13］ WU Huaiqin. Global Stability Analysis of a General Class of Discontinuous Neural Networks with Linear Growth Activation Functions［J］.Information Sciences ，2009 （19）：3432-3441.

［14］ HE K， ZHANG X， REN S， et al. Delving Deep into Rectifiers： Surpassing Human-level Performance on ImageNet Classification［C］∥2015 IEEE International Conference on Computer Vision （ICCV）. Santiago， 2015： 1026-1034.

［15］ KINGMA D， BA J. Adam： a Method for Stochastic Optimization［J］. Computer Science， 2014.

［16］ SRIVASTAVA N， HINTON G， KRIZHEVSKY A， et al. Dropout： a Simple Way to Prevent Neural Networks from Overfitting［J］. Journal of Machine Learning Research， 2014， 15（1）：1929-1958.

［17］ 晏佳伟，胡启，王振振，等. 不同硬化模型对第3代超高强度钢板冲压回弹预测的比较［J］. 上海交通大学学报，2017，51（11）：1334-1339.

YAN Jiawei， HU Qi， WANG Zhenzhen， et al. Comparison of Different Hardening Models for Springback Prediction of the Third Generation Ultra-high Strength Steel Sheet［J］. Journal of Shanghai Jiao Tong University， 2017，51 （11）： 1334-1339.

［18］ 劉雁冰. 车身梁类件冲压回弹分析及控制研究［D］. 重庆：重庆理工大学，2014.

LIU Yanbing. Research on Stamping Springback Analysis and Control of Body Beam Parts ［D］. Chongqing： Chongqing University of Technology， 2014.

［19］ 冯斌，毛建中，胡晖.基于BP神经网络的条带刚凸特征回弹预测［J］.锻压技术，2020，45（3）：20-26.

FENG Bin， MAO Jianzhong， HU Hui. Prediction of Springback Based on BP Neural Network［J］.Forging ＆ Stamping Technology， 2020，45 （3） ： 20-26.