考虑法向接触力变化的机器人砂带磨削参数研究

陈庚 向华 叶寒 肖飞

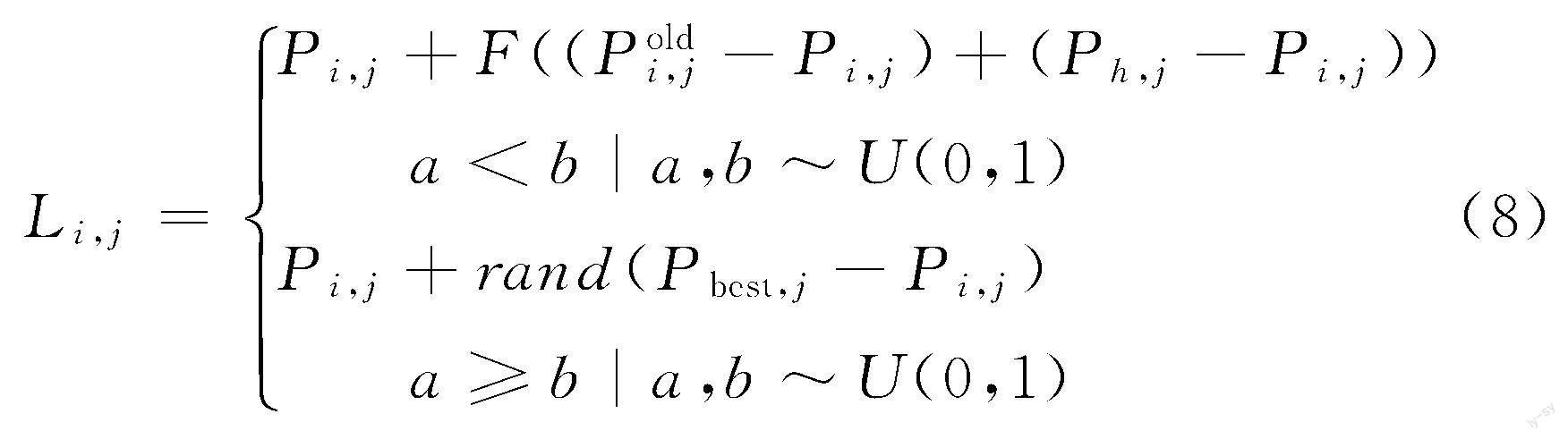
摘要：叶片表面粗糙度与型面尺寸精度对航空发动机整体性能和使用寿命有重要影响，为了解决机器人砂带磨削的切入切出阶段及曲率变化较大部位的法向接触力变化对表面粗糙度和材料去除深度一致性的影响，设计正交中心组合试验并用宽度学习算法建立了磨削工艺参数与表面粗糙度和材料去除深度的预测模型，利用传感器测量的法向接触力与建立的预测模型，结合多重学习回溯搜索算法求解了自适应工艺参数，最后用得到的工艺参数进行了磨削试验，表面粗糙度和材料去除深度的试验值与模型预测值最大误差为14.2%和13.4%，表明所提方法可以保证表面粗糙度和材料去除深度的一致性良好。

关键词：机器人；砂带磨削；法向接触力；工艺参数；自适应技术

中图分类号：TP161

DOI：10.3969/j.issn.1004132X.2023.07.006

Research on Robot Abrasive Belt Grinding Parameters Considering the

Change of Normal Contact Force

CHEN Geng1，2 XIANG Hua1 YE Han3 XIAO Fei3

1.School of Mechanical Science and Engineering，Huazhong University of Science and Technology，Wuhan，430074

2.Foshan Institute of Intelligent Equipment Technology，Foshan，Guangdong，528234

3.School of Advanced Manufacturing，Nanchang University，Nanchang，330031

Abstract： The surface roughness and surface dimensional accuracy of blades had important influence on the overall performance and service life of the aero-engines. In order to solve the influences of the changes of normal contact forces on the surface roughness and the uniformity of material removal depth on the cut-in or cut-out stages of robotic abrasive belt grinding and the changes of normal contact forces on the parts with large curvature changes， orthogonal center combination design （CCD） test was designed and width learning algorithm was used to establish the prediction model of grinding process parameters， surface roughness and material removal depth. The prediction model of normal contact force and surface roughness and material removal depth measured by sensors was used to solve the adaptive processing parameters by combining multiple learning backtracking search algorithm. Finally， grinding tests were carried out with the obtained processing parameters. The maximum errors between the test values of surface roughness and material removal depth and that of the model predictions are as 14.2% and 13.4% respectively. The proposed method may ensure good consistency between surface roughness and material removal depth.

Key words： robot； abrasive belt grinding； normal contact force； processing parameter； adaptive technology

0 引言

葉片作为航空发动机中的一个关键部件，其制造技术一直都是新一代航空发动机研制中首要解决的技术难题［1］。经过精密铣削后的叶片表面留有波峰波谷残留高度和接刀痕［2］，其型面精度和表面粗糙度的一致性对航空发动机在高温高压工况下的使用寿命和动力学性能影响较大，通常采用磨抛工艺来保证叶片型面精度和表面粗糙度［3-4］。国内外常用专用数控机床［5］和手动磨削方式磨削抛光叶片。专用数控机床价格昂贵且适用度不高，而手工磨削不仅环境恶劣、劳动强度大、磨削效率低，且叶片的表面粗糙度和型面精度的一致性难以保证。近年来，因为工业机器人具有灵活性好、适用性强、成本低以及砂带机设备简单和加工质量好等优点，所以工业机器人与砂带机组成的柔性磨抛装备被逐步应用于叶片磨削［6-7］，同时也出现许多技术难点亟待解决，如机器人力控制技术［8-9］、磨削轨迹规划技术［10-11］、表面粗糙度预测建模与优化［12-13］、材料去除率［14-15］与材料去除深度建模与优化［16-17］等。

表面粗糙度和材料去除深度是评判叶片磨削质量的两个重要指标，国内外学者围绕叶片磨削表面粗糙度和材料去除深度开展了许多研究工作。ZHAO等［18］利用响应面法建立了叶片表面粗糙度模型并优化了磨削工艺参数，用优化的参数进行试验得到叶片的表面粗糙度明显降低。淮文博等［19］用响应面法分析了砂布轮抛光叶片时工艺参数与表面粗糙度的关系，同时还考虑了工艺参数对磨削前后表面粗糙度比值的影响规律。SONG等［20］提出采用基于矢量平滑的自适应支持向量机（VFS-SVR）算法建立工件表面曲率、进给速度、法向磨削压力与材料去除率的关系，通过合用粒子群算法优化磨削工艺参数，对材料去除率有较高的预测精度。PANDIYAN等［21］用卷积神经网络建立材料去除深度的预测模型，显著提高了预测精度。这些研究主要围绕磨削过程的表面粗糙度或材料去除深度的单一目标进行，而叶片磨削中不仅要保证表面粗糙度满足工艺要求还要考虑型面的尺寸精度。CHEN等［22］采用灰色关联将叶片磨削中表面粗糙度和材料去除率的多目标优化问题转换成单目标优化问题，用径向基函数神经网络建立工艺参数与灰色相关度的映射关系，然后用因子算法获得最优的工艺参数。ZHU等［23］采用带精英策略的非支配排序的遗传算法（NSGA-Ⅱ）同时优化表面粗糙度和材料去除率，并对优化的工艺参数进行验证。这些工作针对磨削加工中表面粗糙度与材料去除率的多目标优化开展研究。

力控制技术作为机器人砂带磨削系统的一项关键技术，用于控制磨削时砂带与工件的法向接触力，叶片磨削后的表面粗糙度和材料去除深度与法向接触力有较大关系。XU等［24］提出了一种机器人叶片磨削加工中的力控制策略，对比分析了有/无力控制时叶片表面粗糙度的变化趋势，研究表明，法向接触力对叶片磨削后的表面粗糙度和尺寸精度有较大影响。YAN等［25］通过分析磨削中材料去除深度和法向接触力关系，发现在切入/切出阶段由于法向接触力变化在工件表面有过切/欠切现象，影响工件最终磨削的表面质量。XU等［26］考虑接触轮与工件接触的弹性变形及叶片曲率的变化，提出了一个改进的残留高度模型用于评估叶片磨削过程的表面粗糙度，研究表明，不同的工艺参数对叶片表面粗糙度影响效果不一样。这些工作研究了法向接触力对表面粗糙度或材料去除深度的影响效果，但鲜有文献考虑磨削加工中法向接触力变化时如何保证表面粗糙度和材料去除深度的一致性。

机器人夹持工件以预定的速度靠近砂带时，工件与接触轮发生碰撞冲击，导致在切入阶段法向接触力偏离设定的期望力而产生过切，在切出阶段由于工件与砂带分离，法向接触力逐步减小而产生欠切，而且机器人砂带磨削中叶片曲率变化较大部位的法向接触力也较难保持恒定［27］，影响叶片的表面粗糙度和尺寸精度。许多研究通过改善过渡阶段的接触力超调与稳定性来提高该区域的磨削质量［28-29］，然而磨削加工中工件的表面粗糙度和材料去除深度不仅与法向接触力有关，还与砂带线速度、进给速度、砂带的粒度和砂带张紧力等因素有关。为了保证磨削加工的表面粗糙度和材料去除深度的一致性，本文提出一种基于法向接触力变化的工艺参数自适应技术。通过CCD试验数据并结合宽度学习算法建立磨削工艺参数与表面粗糙度和材料去除深度的预测模型，利用机器人磨削系统中力传感器采集的法向接触力数据，在建立的表面粗糙度和材料去除深度模型中，用多重学习回溯搜索算法（ML-BSA）获得满足磨削加工要求的线速度和进给速度，在机器人砂带磨削中法向接触力较难控制的区域，通过调整机器人的进给速度和砂带线速度来保证表面粗糙度和材料去除深度一致。

1 試验设备与试验结果

1.1 试验设备

机器人磨削系统如图1所示，由工业机器人及控制柜、六维力传感器、砂带机及3M金塔砂带、测试工件和夹具等组成。其中，工业机器人的型号为HSR-JR605，额定负载为5 kg，最大工作半径为746 mm，重复定位精度为±0.02 mm；机器人末端安装的HPS-FT060E六维力传感器用于感知叶片磨抛过程的接触力，力传感器XY轴力测量范围为±600 N，精度为±0.2 N，Z轴力测量范围为±1000 N，精度为±0.4 N；砂带机型号为HS-R10-2600，功率为2.2 kW，最高线速度为30 m/s，接触轮直径与宽度分别为60 mm和10 mm，接触轮内层为直径50 mm的铝芯，外层是厚5 mm、硬度HRC30～HRC35的橡胶，砂带的张紧力用压力阀精确调节；采用美国3M公司237AA氧化铝矿砂的金字塔砂带作为磨料，该型砂带具有较高的切削效率和较低的磨削温度，可保证磨削过程中较好的磨削效果；工件材料为TC11（Ti-6.5Al-3.5Mo-1.5Zr-0.3Si）钛合金，该合金在高温下具有良好的抗氧化性能和冷热加工性能，其材料成分和机械性能如表1、表2所示。

1.2 正交中心组合试验结果

机器人砂带磨削中影响表面粗糙度和材料去除深度的主要工艺参数有砂带线速度vs、进给速度vf、法向接触力Fn、砂带的粒度p等，依据单因素试验设计4因素3水平的正交中心组合表并进行试验。用Mitutoyo（SJ-210）的表面粗糙度仪测量工件的表面粗糙度Ra，测量中取样长度为0.8 mm，评定长度为4 mm，在垂直磨削轨迹方向测量5点并取平均值作为最终表面粗糙度。在高精度运动平台上用线激光传感器（LJ-X8020）测量工件的磨削深度h，线激光传感器在Z方向的测量精度是2.5 μm，测量磨削路径上3点的深度值h并取平均作为材料去除深度DMR。表3、表4分别为设计的正交中心组合试验的因素水平表和试验结果。

2 表面粗糙度与材料去除深度建模

2.1 宽度学习算法

宽度学习系统（board learning system，BLS）是基于随机向量函数神经网络算法提出的学习算法［30］，通常由输入层、隐藏层和输出层组成，其网络结构如图2所示。输入数据经过特征映射生成特征节点，特征节点经过非线性变换生成增强节点，特征节点和增强节点组合后作为隐藏层连接输出权重矩阵得到最终的输出结果。宽度学习系统借助广义逆矩阵得到输出层的权重矩阵，该算法因运算速度快、拟合精度高且不会出现梯度消失而被广泛用于图像分类、回归模型预测、模式识别及自动控制等领域。

图2中，X为训练模型的输入数组，X∈Ra×b，Y为训练模型的输出数组，Y∈Ra×c，第i个特征节点表示为zi=φi（XWei+βei），i=1，2，…，n，其中，φi表示激活函数，Wei和βei为随机生成的权重和偏置，所有特征节点组表示为Z（n）=［Z1 Z2 … Zn］；增强节点由特征节点组经过函数映射得到，第j个增强节点表示为Hj=εj（ZWhj+βhj），j=1，2，…，m，其中εj表示激活函数，Whj和βhj为随机生成的权重和偏置，所有增强节点组表示为H（m）=［H1 H2 … Hm］，最后特征节点组和增强节点组拼接后的输入数据表示为A=［Z（n）|H（m）］，经过权值矩阵W（m）映射后的输出表达式如下：

Y=AW（m）（1）

W（m）=（ATA+αI）-1ATY（2）

式中，I为单位矩阵。

用均方根误差来调整模型参数，从而得到最优模型。

2.2 表面粗糙度和材料去除深度建模

在MATLAB2017B中训练宽度学习网络，将隐藏层的特征节点数量Nf设为5，特征窗口数Nw为5，增强节点数Ne为30，激活函数使用的是S型激活函数（sigmoid），训练阶段宽度学习网络的稀疏正则化参数为2～8，增强节点的收缩参数为0.8，分别得到表面粗糙度和材料去除深度的预测模型。

图3和图4分别是砂带粒度p、法向接触力Fn、砂带线速度vs、进给速度vf对表面粗糙度和材料去除深度影响的3D曲面图，将其中2个因素固定在中间水平，分析剩下两个因素（p-Fn，Fn-vs，vs-vf）对Ra和DMR影响效果。从图3a和图4a中可以看出，随p的增大Ra和DMR都减小，这是因为砂带粒度p越大，磨粒越细，参加磨削的磨粒越多，表面粗糙度Ra越小；但越细的磨粒对工件表面的材料去除作用会越弱，因此DMR减小。从图3b和图4b中可以看出，当Fn增大时，Ra和DMR都增大，原因在于当Fn增大时，磨削接触区域内单颗磨粒所受到的平均压力增大，单颗磨粒的切深变大，因此DMR增大；同时随着材料去除能力变强，磨削后工件表面的磨痕变大，Ra也会增大。同时，随vs的增大Ra减小而DMR增大，这是因为当vs增大时，单位时间内参与磨削的磨粒数变多，因而Ra减小；此时磨削区域内磨粒对工件的磨削次数增加，单位时间材料去除效率提高，因此DMR增大。从图3c和图4c中可以看出，随vf的增大，Ra增大而DMR减小，这是因为当vf增大时，单位时间参与磨削的磨粒数减少，与vs增大时的作用效果刚好相反，因此产生的结果也相反，即Ra增大而DMR减小。对比分析图3、图4明显发现，p对Ra的影响最为显著，Fn对DMR的影响最为显著。

为了验证宽度学习算法建立的表面粗糙度和材料去除深度预测模型的准确性，采用回归模型的可决系数来验证拟合效果，表面粗糙度预测模型的可决系数R2=0.991，材料去除深度预测模型的可决系数R2=0.994，可决系数在0～1范围取值，越接近1表示拟合精度越好，因此宽度学习系统建模具有较高的鲁棒性和拟合精度。

3 自适应参数调整策略

机器人磨削的切入切出阶段及工件曲率变化较大部位的法向接触力较难保持恒定，为了减小法向接触力变化对材料去除深度和表面粗糙度一致性造成的影响，利用力传感器测量的法向接触力数据，结合多重学习回溯搜索算法（ML-BSA）求解建立的表面粗糙度和材料去除深度预测模型，对于法向接触力较难保持恒定的部位，通过调整工艺参数来保证表面粗糙度和材料去除深度一致。

3.1 多重学习回溯搜索算法

多重学习回溯搜索算法是一种基于自然进化规律的群体智能算法［31］，由于算法实现简单，具有较强的全局搜索能力和高计算效率等优点，被广泛用于工程问题求解与参数辨识等领域，算法主要包含初始化种群、选择Ⅰ、变异、交叉和选择Ⅱ5个步骤。

（1）初始化种群。在目标函数的搜索空间随机生成当前种群Pi，j和历史种群Poldi，j，表达式为

Pi，j=lowj+rand（upj-lowj）（3）

Poldi，j=lowj+rand（upj-lowj）（4）

i=1，2，…，Nj=1，2，…，D

式中，N为种群的数量；D为所求函数自变量的维数；upj、lowj分别表示对应自变量函数的上下限；rand为［0，1］内随机分布的随机数。

（2）选择Ⅰ。在每次迭代开始时，通过式（5）随机根据当前种群P改变历史种群Pold，然后通过式（6）随机改变Pold中个体的顺序：

其中，a、b为［0，1］之间均匀分布的随机数；permuting函数用来打乱历史种群中个体的顺序。

（3）多重学习。多重学习回溯搜索算法的多重学习主要分为两个部分：依照随机概率一部分个体通过乘以幅度控制矩阵

F=3rndnrndn～N（0，1）（7）

向当前种群和历史种群学习，而另一部分个体则向当前种群的最优个体学习。多重学习方法用于生成新的个体，提高种群的多样性，表达式为

式中，Li，j为多重学习后的变异种群中第i个个体中的第j个变量值；rndn为依照高斯分布随机排列的N×D的随机矩阵。

（4）选择Ⅱ。选择Ⅱ的目的主要是利用贪心机制，在多重学习后的变异个体和原种群中选择更适应更优异的个体来组成新的种群，即

其中，f表示计算个体适应度值的函数，用来判断种群中个体的价值。

（5）精英機制。从当前人群中寻找出最好和最差的个体，使用混沌局部搜索算法围绕当前最佳个体进行变异，如果变异后个体的适应度值优于当前种群中最差的个体，则将该变异后的个体替换掉，表达式为

式中，rand1、rand2为［0，1］范围内随机数；zm为第m次迭代后的混沌因子值，其中混沌因子的初值z0在［0，1］内随机产生；NE为求解评估适应度函数的次数；maxNE为人为设置的求解最大次数。

3.2 自适应工艺参数求解

经过精密铣削的叶片表面留有一定余量，通常采用粗磨—半精磨—精磨等工序获得满足要求的型面精度和表面粗糙度。不同磨削阶段对表面粗糙度和材料去除深度的要求不同，在粗磨阶段关注材料去除深度的一致，而在精磨阶段不仅要保证表面粗糙度还要满足尺寸精度要求。本文结合磨削工艺的实际需求，设计优化目标函数及优化边界条件如下：

min（f）=K1（yRa-ERa）2+K2（yMRD-EMRD）2（12）

4 m/s≤vs≤10 m/s

3 mm/s≤vf≤9 mm/s

p=120，180，240目

式中，ERa、EMRD为期望的表面粗糙度和材料去除深度；yMRD、yRa为通过所建立的材料去除深度和表面粗糙度预测模型所得到的值；K1、K2为表面粗糙度和材料去除深度的权重系数。

假定机器人砂带磨削系统中设定的法向接触力Fn=15 N，过渡阶段的力超调变化范围为±5 N，选取（240目、180目、120目）3组不同粒度的砂带分别进行方法验证，其中设定的表面粗糙度和材料去除深度期望值ERa、EMRD分别对应为（0.44 μm、0.69 μm、0.83 μm）和（0.047 mm、0.059 mm、0.072 mm），优化目标函数的权重系数K1和K2取值为0.1和0.9时，砂带线速度vs和进给速度vf随法向接触力Fn变化曲线如图5所示。

由2.2节分析结论可知，砂带粒度p对表面粗糙度Ra的影响显著，而法向接触力Fn对材料去除深度显著，因此采用不同粒度的砂带进行验证时，砂带线速度vs和进给速度vf随法向接觸力Fn的变化而发生变化，主要保持材料去除深度（MRD）的相对稳定。

当砂带粒度为120目时（图5a），法向接触力从10 N增大到20 N，为保证MRD在期望磨削深度值处稳定，当vf相对稳定时减小vs，当vf增加时vs相对不变，从而抵消法向接触力增大对MRD的影响。当砂带粒度为180目时（图5b），在法向接触力从10 N向20 N增加且进给速度vf减小的情况下，MRD将增加，通过减小线速度vs保持MRD恒定。当砂带粒度为240目时（图5c），在法向接触力从10 N增大到20 N且砂带线速度vs增大的情况下，通过调大进给速度vf保持MRD恒定，参数变化趋势的后半段也类似，因此图5的参数变化趋势符合2.2节的工艺参数建模理论。

3.3 磨削验证试验

为了验证BLS算法建立的预测模型与ML-BSA算法求解工艺参数的有效性，分别在机器人砂带磨削系统中对120目、180目和240目的砂带进行磨削试验，试验工艺参数及结果如表5所示，图6和图7所示分别为不同粒度砂带磨削加工后表面粗糙度和材料去除深度的模型预测值和试验结果

对比。从图6中得到，120目时表面粗糙度相对误差最大7.3%，180目时表面粗糙度相对误差最大8%，240目时表面粗糙度相对误差最大14.2%；从图7中得到，120目时材料去除深度相对误差最大7.8%，180目时材料去除深度相对误差最大13.4%，240目时材料去除深度相对误差最大9.5%。不同粒度的砂带表面粗糙度和材料去除深度的试验值与模型预测值偏差较小，表面粗糙度和材料去除深度最大绝对偏差值分别为0.06 μm和0.007 mm，表面粗糙度和材料去除深度最大误差分别为14.2%和13.4%，满足工艺要求，表明建立的预测模型和得到的自适应工艺参数是有效的。

4 结论

（1）基于4因素3水平的正交中心组合试验，采用宽度学习算法建立磨削工艺参数与表面粗糙度和材料去除深度的预测模型，通过回归模型的可决系数验证模型的准确性，其中表面粗糙度模型可决系数R2=0.991，材料去除深度模型可决系数R2=0.994，结果表明利用宽度学习系统建立的预测模型具有较高的拟合精度和鲁棒性。

（2）利用宽度学习系统建立了表面粗糙度和材料去除深度预测模型，结合ML-BSA算法求解法向接触力变化时保证材料去除深度与表面粗糙度一致时的自适应的工艺参数变化曲线，通过磨削试验得到表面粗糙度和材料去除深度值与模型的预测值对比，表面粗糙度和材料去除深度最大误差分别为14.2%和13.4%，满足磨削加工的精度要求，通过该方法可以保证磨削加工表面粗糙度和材料去除深度的一致性良好。

（3）本文结合BLS算法与ML-BSA算法各自的优点，建立表面粗糙度和材料去除深度的预测模型，利用六维力传感器测量的法向接触力数据优化磨削工艺参数，是一种新颖实用的方法，可以提高机器人砂带磨削系统的加工质量。

参考文献：

［1］ 郭东明， 孙玉文， 贾振元. 高性能精密制造方法及其研究进展［J］. 机械工程学报， 2014， 50（11）：119-134.

GUO Dongming， SUN Yuwen， JIA Zhenyuan. Methods and Research Progress of High Performance Manufacturing［J］. Journal of Mechanical Engineering， 2014， 50（11）：119-134.

［2］ GUO J， SHI Y， CHEN Z， et al. Optimal Parameter Selection in Robotic Belt Polishing for Aeroengine Blade Based on GRA-RSM Method［J］. Symmetry， 2019， 11（12）：1526.

［3］ BIGERELLE M， GAUTIER A， HAGEGE B， et al. Roughness Characteristic Length Scales of Belt Finished Surface［J］. Journal of Materials Processing Technology， 2009， 209（20）：6103-6116.

［4］ 陳贵林， 赵春蓉. 航空发动机精锻叶片数字化生产线［J］. 航空制造技术， 2015（22）：78-83.

CHEN Guilin， ZHAO Chunrong. Digital Production Line of Precision Forging Aeroengine Blade［J］. Aeronautical Manufacturing Technology， 2015（22）：78-83.

［5］ MOUMEN M， CHAVES-JACOB J， BOUAZIZ M， et al. Optimization of Pre-polishing Parameters on a 5-axis Milling Machine［J］. The International Journal of Advanced Manufacturing Technology， 2016， 85（1）：443-454.

［6］ 蔺小军， 杨艳， 吴广， 等. 面向叶片型面的五轴联动柔性数控砂带抛光技术［J］. 航空学报， 2015， 36（6）：2074-2082.

LIN Xiaojun， YANG Yan， WU Guang， et al. Flexble Polishing Technology of Five-axis NC Abrasive Belt for Blade Surface［J］. Acta Aeronautica et Astronautica Sinica， 2015， 36（6）：2074-2082.

［7］ WEI W， CHAO Y U N. A Path Planning Method for Robotic Belt Surface Grinding［J］. Chinese Journal of Aeronautics， 2011， 24（4）：520-526.

［8］ CHEN F， ZHAO H， LI D， et al. Contact Force Control and Vibration Suppression in Robotic Polishing with a Smart End Effector［J］. Robotics and Computer-integrated Manufacturing， 2019， 57：391-403.

［9］ ZHU D， XU X， YANG Z， et al. Analysis and Assessment of Robotic Belt Grinding Mechanisms by Force Modeling and Force Control Experiments［J］. Tribology International， 2018， 120：93-98.

［10］ ZHANG T， SU J. Collision-free Planning Algorithm of Motion Path for the Robot Belt Grinding System［J］. International Journal of Advanced Robotic Systems， 2018， 15（4）：1-13.

［11］ NG W X， CHAN H K， TEO W K， et al. Capturing theTacit Knowledge of the Skilled Operator to Program Tool Paths and Tool Orientations for Robot Belt Grinding［J］. The International Journal of Advanced Manufacturing Technology， 2017， 91（5）：1599-1618.

［12］ QU C， LYU Y， YANG Z， et al. An Improved Chip-thickness Model for Surface Roughness Prediction in Robotic Belt Grinding Considering the Elastic State at Contact Wheel-workpiece Interface［J］. The International Journal of Advanced Manufacturing Technology， 2019， 104（5）：3209-3217.

［13］ ZHAO T， SHI Y， LIN X， et al. Surface Roughness Prediction and Parameters Optimization in Grinding and Polishing Process for IBR of Aero-engine［J］. The International Journal of Advanced Manufacturing Technology， 2014， 74（5）：653-663.

［14］ WU S， KAZEROUNIAN K， GAN Z， et al. A Material Removal Model for Robotic Belt Grinding Process［J］. Machining Science and Technology， 2014， 18（1）：15-30.

［15］ WANG Y J， HUANG Y， CHEN Y X， et al. Model of an Abrasive Belt Grinding Surface Removal Contour and Its Application［J］. International Journal of Advanced Manufacturing Technology， 2016， 82（9/12）：2113-2122.

［16］ YANG Z， CHU Y， XU X， et al. Prediction and Analysis of Material Removal Characteristics for Robotic Belt Grinding Based on Single Spherical Abrasive Grain Model［J］. International Journal of Mechanical Sciences， 2021， 190：106005.

［17］ WANG P， GAO R X， YAN R. A Deep Learning-based Approach to Material Removal Rate Prediction in Polishing［J］. CIRP Annals—Manufacturing Technology， 2017， 66：429-432

［18］ ZHAO T， SHI Y， LIN X， et al. Surface Roughness Prediction and Parameters Optimization in Grinding and Polishing Process for IBR of Aero-engine［J］. The International Journal of Advanced Manufacturing Technology， 2014， 74（5）：653-663.

［19］ 淮文博， 史耀耀， 唐虹， 等. 砂布輪抛光叶片表面粗糙度预测与参数优化［J］. 计算机集成制造系统， 2017， 23（12）：2708-2718.

HUAI Wenbo， SHiyaoyao， TANG Hong， et al. Surface Roughness Prediction and Processing Parameters Optimization in Abrasive Cloth Wheel Polishing Process for Blade［J］. Computer Integrated Manufacturing Systems， 2017， 23（12）：2708-2718.

［20］ SONG Y， LIANG W， YANG Y. A Method for Grinding Removal Control of a Robot Belt Grinding System［J］. Journal of Intelligent Manufacturing， 2012， 23（5）：1903-1913.

［21］ PANDIYAN V， MURUGAN P， TJAHJOWIDODO T， et al. In-process Virtual Verification of Weld Seam Removal in Robotic Abrasive Belt Grinding Process Using Deep Learning［J］. Robotics and Computer-integrated Manufacturing， 2019， 57：477-487.

［22］ CHEN Z， SHI Y， LIN X. Enhanced Material Removal Rate and Surface Quality in Ti-6Al-4V Blisk Blade Polishing by GRA-RBF-FA Method［J］. Surface Review and Letters， 2019， 26（9）：1950062.

［23］ ZHU C， GU P， WU Y， et al. Surface Roughness Prediction Model of SiCp/Al Composite in Grinding［J］. International Journal of Mechanical Sciences， 2019， 155：98-109.

［24］ XIAOHU X U， DAHU Z H U， ZHANG H， et al. Application of Novel Force Control Strategies to Enhance Robotic Abrasive Belt Grinding Quality of Aero-engine Blades［J］. Chinese Journal of Aeronautics， 2019， 32（10）：2368-2382.

［25］ YAN S， XU X， YANG Z， et al. An Improved Robotic Abrasive Belt Grinding Force Model Considering the Effects of Cut-in and Cut-off［J］. Journal of Manufacturing Processes， 2019， 37：496-508.

［26］ XU X H， YE S T， YANG Z Y， et al. Analysis and Prediction of Surface Roughness for Robotic Belt Grinding of Complex Blade Considering Coexistence of Elastic Deformation and Varying Curvature［J］. Science China Technological Sciences， 2021， 64（5）：957-970.

［27］ 甘亚辉， 段晋军， 戴先中. 非结构环境下的机器人自适应变阻抗力跟踪控制方法［J］. 控制与决策， 2019， 34（10）：2134-2142.

GAN Yahui， DUAN Jinjun， DAI Xianzhong. Adaptive Variable Impedance Control for Robot Force Tracking in Unstructured Environment［J］. Control and Decision， 2019， 34（10）：2134-2142.

［28］ 邢宏軍， 丁亮， 高海波， 等. 基于阻抗控制的机器人旋拧阀门轴向位置自适应跟踪［J］. 机械工程学报， 2019， 55（15）：124-134.

XING Hongjun， DING Liang， GAO Haibo， et al. Adaptive Tracking of Axial Position for Valve-turning with a Robot Based on Impedance Control［J］. Journal of Mechanical Engineering， 2019， 55（15）：124-134.

［29］ LIANG X， ZHAO H， LI X， et al. Force Tracking Impedance Control with Unknown Environment via an Iterative Learning Algorithm［J］. Science China Information Sciences， 2019， 62（5）：1-3.

［30］ CHEN C L P， LIU Z. Broad Learning System：an Effective and Efficient Incremental Learning System without the Need for Deep Architecture［J］. IEEE Transactions on Neural Networks and Learning Systems， 2017， 29（1）：10-24.

［31］ YU K， LIANG J J， QU B Y， et al. Multiple Learning Backtracking Search Algorithm for Estimating Parameters of Photovoltaic Models［J］. Applied Energy， 2018， 226：408-422.