航天用大展收比豆荚结构变形规律模型及其仿真验证

杨硕 张杰 孔宁 王浩威 王晓宇 庄原

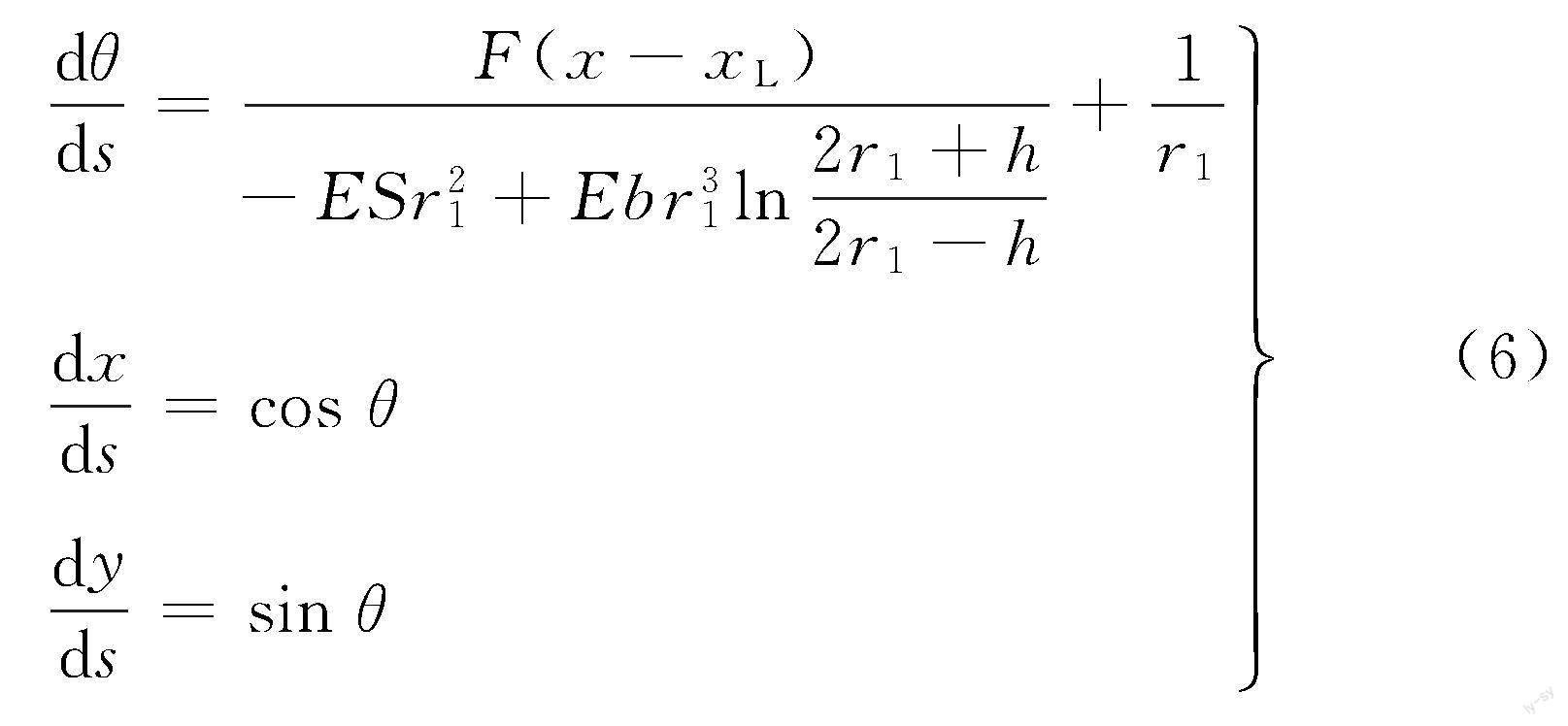
摘要：豆荚结构又称可盘卷管状伸展臂，是一种具有大展收比的弹性伸展结构，可以被压缩成板状装载在航天器上，需要时自行展开为空心筒，用于展开太阳翼、卫星天线等组件，能够缩小航天器发射时的体积。设计豆荚结构尺寸时需要考虑其力学性能。针对豆荚结构收纳过程中力学特性影响因素变化多、计算量大等问题，利用力学分析设计了一种数值模型，可以计算不同尺寸参数的豆荚结构整个压缩过程中的压缩力变化。利用有限元分析软件ABAQUS对压缩变形进行仿真分析，对比数值模型的计算结果与仿真结果误差小于10%。通过数值模型分析得到了豆荚结构尺寸参数对压缩力的影响。

关键词：豆荚结构；空间伸展机构；力学性能；仿真分析

中图分类号：V423.6

DOI：10.3969/j.issn.1004132X.2023.07.003

Deformation Law Model and Simulation Verification of Pod Structures with

Large Exhibition-to-receive Ratio for Aerospace Applications

YANG Shuo1 ZHANG Jie1 KONG Ning1 WANG Haowei2 WANG Xiaoyu2 ZHUANG Yuan2

1.School of Mechanical Engineering，University of Science and Technology Beijing，Beijing，100083

2.Beijing Institute of Spacecraft System Engineering，Beijing，100094

Abstract： The pod rod， also named as CTM（collapsible tubular mast）， was an elastic stretching structure with large exhibition-to-receive ratio. It might be compressed into a plate and loaded on the spacecraft and self-deployed into a hollow cylinder when needed， which might be used to expand solar wings， satellite antennas and other components， and might reduce the volume of spacecraft during launch. The mechanics properties of pod structure should be considered when designing the structure size. A numerical model was established by means of mechanics analysis in order to solve the problems of large amount of calculation， and frequent variation of the factors that affecting mechanics properties. The numerical model might be applied to calculate the compressive force variation during the entire compression processes for the pod structure with different size parameters. The finite element analysis software ABAQUS was used to simulate and analyze the compression deformation. The deviations between the calculation results and the simulation ones are less than 10%. The influences of size parameters of the pod structure on the compressive force were obtained through numerical model analyses.

Key words： pod structure; space deployment mechanism; mechanics property; simulation analysis

0 引言

隨着空间探索任务的发展，航天器需要实现的功能越来越多，其空间构型日趋复杂化、大型化［1］。豆荚杆等空间伸展机构可以设计为在航天器发射及动力飞行阶段能紧密可靠地收纳于有限的包容空间内，而在动力飞行阶段结束后在航天器的工作轨道上伸展为预定的空间构型来工作，提高航天器在发射阶段的强度，节约发射成本［2］。

空间伸展机构的概念始于20世纪60年代，由美国航空航天局（NASA）率先提出，1975年，空间伸展机构作为磁强计支架首次用于美国空军S23卫星后，各类航天器开始装配不同展开原理的伸展机构。迄今为止，各国已经在各个航天器上使用过数十种不同种类的空间伸展机构，而空间伸展机构也成为空间科学技术的重要研究方向［3］。

豆荚结构是空间伸展机构中薄壁管伸展臂的一种经典结构，又被称为可盘卷管状伸展臂（collapsible tubular mast，CTM），因其外形又被称为豆荚杆，本文称该结构为豆荚结构。NASA、ESA已成功研制并验证多种基于豆荚结构展开机构的太阳帆［4-5］，验证了其展收作用的可靠性。由于豆荚结构具有使用方便、性能可靠、蓄能能力强、展收比大等优点，在航天领域乃至其他机械机构领域都有着较为广泛的使用需求［6-7］。豆荚结构主要依靠曲板结构的压平与自身弹性伸展来实现伸展与压缩［8］，具有很大的展收比，可以为航天器压缩大量空间。设计薄壁管伸展臂的结构尺寸需要了解其机械性能，研究薄壁管伸展臂结构压缩时的力学特性。姬鸣［9］设计了一种薄壁管伸展臂结构展开薄膜天线，并利用有限元软件校核关键元件的强度与刚度。房光强等［10］采用样机实验判断了薄壁管伸展臂的收纳与展开具有较高的可重复性与稳定性。李冰岩等［11］采用数学解析的方法判断薄壁管伸展臂的性能参数，从而结合设计要求，设计伸展臂的几何参数。以上研究主要针对非金属材料豆荚结构变形过程进行试验研究，可在此基础上开展不同材料豆荚结构变形规律的研究。

设计一种简单可靠的计算方法，根据豆荚结构的尺寸参数计算力学性能，可以节约大量设计时间与成本。本文在已有研究的基础上，结合几何分析的方法［12-14］对豆荚结构的压缩过程进行力学解析，得到压缩力随压缩行程变化规律的计算方法。利用ABAQUS软件分析豆荚结构应变变化规律，采用控制变量法仿真不同曲率与厚度的豆荚结构力学特性，并对本计算方法的结果进行仿真验证。

1 薄壁管伸展结构压缩变形分析

本研究团队设计制造的钛合金豆荚结构外形如图1所示。该结构主要由八段相同曲率与弧度的弧形板组成，在压缩过程中，各个弧形板的曲率减小，直至被压为平板，实现该结构由立体空心筒构型到平面板形构型的转变，继而将被压扁平的结构卷起来节约空间。展开时，在自身弹性力作用下，豆荚结构重新张开为压缩前空心筒的形状。

由于豆荚结构的变形在轴向上完全相同，因此研究该结构的压缩力变化特性可以研究其轴向视图，将变形简化为平面变化。豆荚结构压缩过程中轴向视图的具体表现形式见图2（顺序从左到右，再从上到下）。可以发现豆荚杆结构的变形具有对称性，表现为横向与纵向均保持轴对称。

2 豆荚结构收纳过程中力学特性分析

为了得到豆荚结构压缩过程的力学特性，需要对该结构变形过程的力学过程进行解析，得到可以反映豆荚结构力学性能的函数数值模型。

由于豆荚杆结构在压缩过程中保持对称结构，因此在研究其力学特性时只需要压缩1/4部分即图3中ABC弧段。ABC弧段由两段弧形结构AB与BC组成，两段结构保持为关于B点的中心对称。纵向压缩过程中，豆荚结构受到平板压缩，在压缩过程早期仅在最外侧的A、D两点受到压缩力F。而弧段ABC由于在A点与C点均与其他部分连接，无法弯曲，所以可以视作在A点与C点固定，B点自由的弧形悬臂梁形式，并且在B点受纵向压缩力F/2（豆荚结构左右对称，一侧只受到压缩力F的一半）作用，使得弧段的曲率减小，两端纵向距离减小。

利用上述解析方法可以将豆荚结构压缩变形过程简化为单段弧形悬臂梁受纵向力变形的过程，极大地降低了计算难度。然而这个方法有其局限性，即该结构的前提是平板压缩豆荚结构时，受力点仅作用在A、D两点。压缩早期豆荚结构纵向最外侧仅A、D两点受力，但是随着压缩作用的进行，A、D两点处的曲率不断减小，直至降为0。若按照弧形悬臂梁模型计算，A、D两点处的曲率变为负值，形状上呈现A、D两点纵向内凹，那么此时压縮力将无法作用在A、D两点，弧形悬臂梁模型不成立。因此，在A、D两点曲率降为0时（此时该处的应变值称为“压平应变值”，数值为板厚与两倍曲率半径的商值），压缩量称为“边界临界值”，从此处开始需要更改力学模型。

假设当A、D两点的应变达到压平应变值时不再升高。弧形悬臂梁模型中，悬臂梁固定端应变最大，向自由端逐渐降低，随着压缩的进行，应变较低处的应变值会升高至压平应变值后停止。该过程持续进行，直至整段弧段ABC曲率都减小为0，即被压为平板，整个压缩过程完成，具体过程见图4。在此基础上，建立了豆荚结构压缩后期的简化力学变形模型［15］。

需要说明的是，图4中的模型对变形作了适当简化，如压平段在压平完成前会具有一定波动形状，也会产生内凹现象。然而由于内凹现象轻微，因此忽略该现象的影响。

明确了豆荚结构压缩变形过程，可将该变形过程分为变形前期弧形悬臂梁模型及后期压平变形模型，下面具体研究豆荚结构变形过程的力学特性。

按照上述解析，将一个豆荚结构视作8块弧形板AB拼接而成，且8块弧形板受力情况相同。设该豆荚结构尺寸如图5所示，单片弧形板弧长为L，曲率半径为r1，厚度为h，豆荚结构的轴向长度为b。

取一片弧形板可以视作一端固定一端自由的悬臂梁，自由端受到纵向力F作用，整个悬臂梁发生大挠度变形，省略梁弯曲中性层与几何中轴之间的差异，如图6a所示。取弧形板一段弧度为θ1，轴线半径为r1的梁单元，变形后弧度变为θ2，轴线半径为r2，示意图见图6b。

梁单元的原长为几何中轴的弧长L，变形前后弧长不变，即

L=r1θ1=r2θ2（1）

则曲率径向上与几何中轴距离为y的应力σ为

式中，E为悬臂梁材料的弹性模量；ε为y处的应变。

计算截面积为S的梁上的正应力FN与弯矩M如下：

将上式变形可得该梁单元变形后的曲率半径r2与悬臂梁转角θ与变形后悬臂梁弧长s之间的关系：

故本模型中存在如下关系：

式中，x、y为变形后梁单元距离固定端的横纵坐标位置；xL为变形后梁自由端的横坐标。

坐标图见图6a。

将式（6）中的第一式对弧长s求导，并利用式（6）中的后二式可得

易知悬臂梁压平前，自由端的转角最大，设此处转角θ=θL，且曲率半径不变，即dθ/ds=1/r1，可得积分常数项：

将式（10）代入式（9）可得

即

式（12）求积分，根据边界条件，当F=0、θL=60°时，s=L，可得

其中，c为常数多项式，完整展开式为c=br1ln（（2r1+h）/（2r1－h））－S，θL可由下式计算：

式中，Δ为粱中轴的长度变化量。

采用工程应变的定义，则Δ可由下式计算：

通过式（14）与式（15）可以计算得到梁变形后构形的最大转角θL以及纵向压缩力F。由于计算时对中性层位置进行简化，故压缩力F在计算结果的基础上设置1.1的修正系数。

计算得到梁变形后构形的最大转角θL，继而得到变形后梁的横向、纵向位置xc与yc：

已知弧形板变形后位置，可以利用弧形板变形前的横向纵向位置计算豆荚结构横向纵向的变形量x与y：

上述数值模型计算豆荚结构力学特性的方法命名为“弧形悬臂梁模型法”，该方法可计算得到弧形板ABC的应力分布情况，发现自由端应力值较小，固定端应力值较大。当豆荚结构应力最大处的曲率为0时，变形力学模型如图7所示。

豆荚结构的最大应力处被压缩至曲率为0时，随着变形量的增大，压平接触面积逐渐增大。结合有限元分析结果作出如下假设：

（1）未压平的部分弧形板等效弧度值φ大小可由下式计算：

（2）压力集中在变形区域的边缘，由于该模型完全绕点O对称，所以设置力臂为l，计算公式如下：

l=r1sin φ（20）

（3）由于该模型计算结果与弧形板悬臂梁计算结果在边界临界值处y1产生阶跃，为使模型更接近真实变形情况，可以使用弧形板悬臂梁解析公式在边界临界值y1的压缩力F1，对该模型计算结果边界值进行修正，引用式（18）为该模型引入修正系数μ，μ为式（18）计算的压缩力F1与纵向变形量为y1时式（20）计算的M/L的比值：

式中，I为梁截面的惯性矩，I=bh3/12。

上述数值模型计算豆荚结构力学特性的方法称为“压平模型法”，将“弧形悬臂梁模型法”与“压平模型法”两种模型结合，可以得到不同纵向压力F下豆荚结构的纵向变形量y，进而确定豆荚结构压缩过程的力学特性。

3 豆荚结构有限元仿真验证

3.1 应变与力变化规律研究

利用ABAQUS建立仿真模型，验证上述豆荚结构力學特性解析计算方法的正确性。首先研究豆荚结构在压缩与回弹过程中应变与力的变化规律。

模型主要由豆荚结构以及两块平板组成，为了方便说明，同样将豆荚结构按图3进行分段。豆荚结构的曲率半径为5 mm，厚度为0.2 mm，轴向长度20 mm，具体形状见图8。结构材料选用钛合金，弹性模型为110 GPa，泊松比为0.3，密度为4.5×103 kg/m3。

为模型豆荚结构与上下平板之间、豆荚结构轴内表面之间添加表面接触约束，上平板表面耦合其几何中心参考点RP-1。分析步类型选择静力通用分析，总分析时间为2 s，每个分析步长为0.05 s，每步下压量相同，在1 s时达到最大下压量，之后结构逐渐回弹，直至2 s时恢复到压缩前的初始状态。边界条件设置纵向下平板表面完全固定，控制上平板表面耦合点RP-1向下压缩后回弹，最大下压量为9.8 mm，压缩过程如图9所示，为方便观察压缩过程的应力分布情况，隐藏上平板。

观察图9豆荚结构压缩过程的应变云图变化情况，图9f即豆荚结构被完全压平时的应变云图，最大应变值约为2.1%，当模型板厚0.2 mm、曲率半径5 mm时，计算压平应变值为2%，两者结果相近。分析豆荚结构的压缩过程图9a～图9f，有限元仿真得到的应变分布变化情况与解析模型类似，可分为两个阶段：

（1）图9a～图9d所示阶段，压缩过程前0.7 s，弧段AB呈现A端应变较高，越接近B端应变越小的分布情况，类似于图3中A端固定，B端自由并且在B端施加载荷的悬臂梁模型，弧段BC同理。豆荚结构上分布的最大应变值随压缩行程逐渐升高，在第0.7 s时应变值达到2.0%，近似等于压平应变值。

（2）图9d～图9f所示阶段，在后续0.3s的压缩过程中，最大应变值没有明显变化，最高达到2.26%，稍高于压平应变值，说明豆荚结构不会发生大幅度内凹现象。最大应变值的分布范围从A、C点向B点扩散，最终形成图9f中整个AB弧段分布相同大小的应变情况，与图4简化的变形模型相同。整个压缩过程中，豆荚两段圆弧AB与BC的应变都呈大小相等、正负相反的对称特性。

上述豆荚结构的应变云图变化情况与第2节豆荚结构压缩变化的力学模型解析基本类似，可以分为曲板应变达到压平应变值前，弧段AB应变值一端高一端低的“弧形悬臂梁模型法”，与曲板最大应变达到压平应变值后，逐步使整弧段AB呈现压平应变值的“压平模型法”。

分析豆荚结构的回弹过程，如图9f～图9h所示。图9g中，t=1.3 s时刻的应变云图与图9d中t=0.7 s时刻的图相似，提取完整压缩与回弹仿真结果中上平板表面耦合点RP-1受到的反作用力，其变化规律如图10所示。结果显示变化曲线关于t=1 s时刻的轴对称，在压缩阶段，力随变形行程不断增大，而在回弹阶段是压缩阶段的反过程，力则以类似的变化速度随变形行程不断减小，直至为0。

图10表明，针对豆荚结构压缩过程中力的变化规律的数值模型同样适用于该结构在回弹过程中的力学规律。反作用力随压缩行程而增大、随回弹行程而减小的特性也验证了该结构不会在变形过程中发生失稳现象。

3.2 力学特性数值模型验证

根据上述关于豆荚结构的仿真分析，豆荚结构在压缩变形过程中，应变变化规律与几何分析中建立的力学模型表现形式相同，接下来提取有限元模型压缩力变化曲线，与本文推导的函数关系式（18）与式（21）的计算结果进行对比验证。

计算表1中2种不同规格尺寸的豆荚结构，材料性能与边界条件都和3.1节的设置相同，进行仿真运算，提取耦合点RP-1的纵向支反力与纵向位移，将豆荚结构的规格尺寸参数与材料性能参数代入解析所得豆荚结构压缩过程中的力学特性函数关系式（18）、式（21）中，可计算得到纵向压缩量y与压缩力F之间的关系，并进行对比，验证本文提供的解析方法计算豆荚结构压缩过程中的压缩力与压缩行程之间关系的准确性。

将2种规格的豆荚结构压缩力仿真结果与本文的解析结果进行对比，得到压缩力变化曲线，如图11所示。由上述2种规格的豆荚子结构也可以提取得到其压缩刚度的变化曲线，如图12所示。

从图11与图12中可以发现，无论是压缩力变化曲线还是压缩刚度变化曲线，本文提供的计算方法在各个规格尺寸的豆荚结构的应用上都与仿真曲线相似，厚度为0.1～0.3 mm、曲率半径为5～15 mm的常规尺寸豆荚结构计算与仿真结果的压缩力误差小于10%，验证了本文解析结果的可靠性。

同时，豆荚结构在压缩过程中，不仅力学模型具有阶段性，压缩力与压缩刚度曲线也明显具有相应的阶段性：约整个压缩过程前2/3阶段内，即“悬臂梁模型法”解析段，压缩力曲线呈稳定上升趋势，上升斜率即压缩呈下降趋势，但下降值小于初始刚度值1/3；压缩过程后1/3阶段内，即“压平模型法”解析段，压缩力与压缩刚度曲线都急剧升高。

4 豆荚结构参数对压缩力的影响

首先分析“悬臂梁模型法”解析段的压缩力影响关系，从式（18）中提取关于纵向压缩量y的关系式。由于曲率半径不同，结构的总压缩行程不同，所以采用行程量纲一形式，将纵向压缩量y与曲率半径r1的比值作为量纲一纵向压缩量y′：

对式（22）等式两边的转角θ进行微分，经过变形得到下式：

式（23）中，相同量纲一纵向压缩量y′下，弧形板的位置转角θ与最大转角θL均相同，因此决定压缩力F的大小主要取决于多项式c：

b［r1（ln（2r1+h）－ln（2r1－h））－h］（24）

压缩力F与豆荚杆轴向长度b成正比毋庸置疑，求解下式中与豆荚结构曲率半径r1与板厚h之间的关系：

f（r1，h）=r1（ln（2r1+h）－ln（2r1－h））－h（25）

式中，r1为豆荚结构压缩变形前的曲率半径，h为板厚，两者都是正数且r1远大于h。

对式（25）中的厚度h进行多阶求导：

将式（25）根据麦克劳林公式展开可得

再分析“压平模型法”解析段的压缩力影响关系，将式（21）变形得

根据式（27）与式（28）可得，在豆荚结构整个压缩过程中，相同量纲一纵向压缩量y′下，压缩力F均与厚度h的立方成正比，与曲率半径r1的平方成反比。具体验证工况参数如表2所示。

当豆荚结构压缩行程或量纲一压缩行程相同时，使用表2中的尺寸参数计算其压缩力，比较厚度与曲率半径对压缩力的影响，如图13所示。图13a横坐标为实际纵向压缩行程量，图13b横坐标采用量纲一形式。

观察图13a可得厚度0.3 mm与0.2 mm之间豆荚结构的压缩力比值η1为3.375，厚度0.3 mm与0.1 mm之间的压缩力比值η2为27，豆荚结构压缩力与板厚的立方成正比成立。图13b中，曲率半径5 mm与10 mm之间的豆荚结构压缩力比值m1为4，曲率半径5 mm与15 mm之间的压缩力比值m2为9，豆荚结构压缩力与曲率半径的平方成反比成立。

5 结论

本文采用力学分析建立了一种可用于研究航天用大展收比豆荚结构变形规律的数值计算模型，并采用有限元仿真验证了其模型准确性，得出结论如下：

（1）通过解析法建立豆荚结构压缩过程中压缩力与压缩行程之间的数值模型，计算结果与仿真结果的压缩力误差小于10%。在设计豆荚结构尺寸时，使用本数值模型可节约大量设计时间与成本。

（2）豆荚结构压缩过程前2/3阶段内，压缩力呈稳定增大趋势，压缩刚度则呈减小趋势，减小值小于初始刚度值的1/3；压缩过程后1/3阶段内，压缩力与压缩刚度均急剧增大。整个变形过程的力学特性呈现“悬臂梁模型”与“压平模型”相结合的变化规律。

（3）豆荚结构在相同量纲一压缩行程时压缩力的大小与厚度的立方成正比，与曲率半径的平方成反比。在设计豆荚结构尺寸时，可量化控制厚度与曲率半径，实现力学性能的预设计，可为豆荚结构的设计工作提供设计参照和理论指导。

参考文献：

［1］ 金国光，刘又午，王树新，等.帶有空间伸展机构的复杂航天器柔性多体动力学分析［J］.中国机械工程，2000， 11（6）：650-653.

JIN Guoguang， LIU Youwu， WANG Shuxin， et al. Analysis of Flexible Multi-body Dynamics of Complex Spacecraft with Spatial Unfolded Mechanism［J］. China Mechanical Engineering，2000，11（6）：650-653.

［2］ 董吉洪，陈小伟.空间相机主镜展开机构设计方案分析［J］.中国机械工程，2012，23（14）：1667-1670.

DONG Jihong， CHEN Xiaowei. Analysis on Design Strategies of Lager-aperture Deployable Primary Mirror of Space Telescopes［J］.China Mechanical Engineering， 2012，23（14）：1667-1670.

［3］ GREENBERG H S， ENGLER E E. Development of Deployable Truss Concept for Space Station［C］∥ESA Proceedings of an International Conference on Spacecraft Structures. Toulouse，1985：19870001490.

［4］ BLOCK J， STRAUBEL M， WIEDEMANN M. Ultralight Deployable Booms for Solar Sails and Other Large Gossamer Structures in Space［J］. Acta Astronautica， 2011，68（7/8）：984-992.

［5］ 冉江南，韩佩彤，曹子振，等.薄壁管状空间伸展臂技术综述［J］.机械，2019，46（10）：44-51.

RAN Jiangnan， HAN Peitong， CAO Zizhen， et al. Overview of Thin-walled Tubular Space Deployable Masts［J］. Machinery， 2019，46（10）：44-51.

［6］ BAI Jiangbo， XIONG Junjiang， GAO Junpeng， et al. Analytical Solutions for Predicting in-plane Strain and Interlaminar Shear Stress of Ultra-thin-walled Lenticular Collapsible Composite Tube in Fold Deformation［J］. Composite Structures， 2013， 97：64-75.

［7］ CHU Zhongli， LEI Yian. Design Theory and Dynamic Analysis of a Deployable Boom［J］. Mechanism & Machine Theory， 2014， 71：126-141.

［8］ BELVIN W K， STRAUBEL M， WILKIE W K， et al. Advanced Deployable Structural Systems for Small Satellites［C］∥NATO CSO STO Specialist Meeting AVT-257 /RSM-041 on Best Practices for Risk Reduction for Overall Space Systems. Zaragoza， 2016：20170003919.

［9］ 姬鸣.薄膜天线支撑杆展开机构的研制［D］. 哈尔滨：哈尔滨工业大学，2011.

JI Ming.Development of Deployment Mechanism for CFRP Booms of the Membrane Antennas［D］. Harbin：Harbin Institute of Technology，2011.

［10］ 房光强，彭福军.航天器可展开支撑杆的研制及其收拢展开特性研究［J］.材料工程，2009（增刊2）：157-160.

FANG Guangqiang， PENG Fujun. Fabrication and Retraction / Deployment Testings of Space Deployable Booms［J］. Journal of Materials Enginee-ring， 2009（S2）：157-160.

［11］ 李冰岩，刘荣强，从强，等.基于豆荚杆的三棱柱式可展开薄膜支撑臂设计与优化［J］.机械工程学报，2020，56（7）：35-43.

LI Bingyan， LIU Rongqiang， CONG Qiang， et al. Design and Optimization of a Tri-prism Deployable Membrane Support Arm Using Lenticular Collap-sible Composite Tubes［J］. Journal of Mechanical Engineering， 2020，56（7）：35-43.

［12］ 曹天捷.集中力作用下悬臂梁几何中轴的弹性大挠度分析［J］.中国民航大学学报，2007，25（5）：53-56.

CAO Tianjie. Analysis of Large Deflection of Geometric Central Axis of an Elastic Cantilever Subjected to Concentrated Force［J］. Journal of Civil Aviation University of China， 2007， 25（5）：53-56.

［13］ 孫江宏，易源霖，赵秋玲，等.MEMS中变截面梁弯曲数学模型的建立［J］.中国机械工程，2014，25（22）：3061-3065.

SUN Jianghong， YI Yuanlin， ZHAO Qiuling， et al. Mathematical Modeling of Variable Cross-section Beam Bending in MEMS［J］.China Mechanical Engineering，2014， 25（22）：3061-3065.

［14］ 栾丰，余同希. 悬臂梁在倾斜载荷作用下的弹塑性大挠度分析［J］.应用数学和力学， 1991， 12（6）：515-522.

LUAN Feng， YU Tongxi. An Analysis of the Large Deflection of an Elastic-Plastic Cantilever Subjected to an Inclined Concentrated Force［J］. Applied Mathematics and Mechanics， 1991， 12（6）：515-522.

［15］ 高冀峰，胡建辉，陈务军，等.透镜式薄壁CFRP管压扁力分析［J］.宇航学报，2017，38（5）：467-473.

GAO Jifeng， HU Jianhui， CHEN Wujun， et al. Analysis of the Flattening Force of Thin-walled Lenticular CFRP Booms［J］. Journal of Astronautics， 2017，38（5）：467-473.