轻量级密码LEA的唯密文故障分析
张金煜,张雨希,李 玮
(东华大学 计算机科学与技术学院, 上海 201620)
随着物联网的迅速发展,越来越多的智慧车辆、智能家居以及移动便携式设备等具有数据交换功能的智能物理对象逐渐接入互联网,给人们的生活、学习和工作带来了极大的便利。然而,物联网安全仍是具有挑战性的问题[1-2]。现阶段人们通常采用基于数学函数的密码来处理并保护未经授权的内容。然而,传统的密码算法一般需要较多资源来执行,难以有效在资源受限的物联网设备中实现数据安全保护。为了能在物联网设备上进行加解密、认证和完整性保护等,国内外研究学者设计了一系列适合物联网的轻量级密码算法[3-6]。
常见的轻量级密码结构有代换置换网络(substitution-permutation network,SPN)、Feistel、ARX等。与其他结构不同,ARX结构仅由模加、循环移位和异或3种运算组成,通过线性与非线性操作的反复迭代,对差分分析、线性分析等密码分析方法具有较强的抵抗能力,常见的ARX结构密码有LEA、SPECK等[5-6]。LEA轻量级密码是2013年Hong等[6]提出的一种具有ARX结构算法的密码,目前它不仅是国际ISO/IEC 29192-2∶2019轻量级密码标准,也是韩国KS X 3246密码标准。LEA密码具有硬件吞吐量少、代码量小等优势,可以在物联网等移动设备上实现高速加密。当前针对LEA密码的分析包括差分分析、线性分析、截断差分分析、飞去来器分析和差分故障分析等[6-11]。
故障分析利用密码设备泄露的错误信息攻击密码系统,由Boneh等[12]于1997年提出并应用于RSA密码的破译。故障分析通常采用电压毛刺和激光脉冲等方式在设备运行密码算法时向其注入故障,并利用获得的错误信息攻击密码。故障分析在发展历程中衍生出唯密文故障分析、差分故障分析、代数故障分析、中间相遇故障分析等方法,对现代密码的安全实现提出了严峻的挑战[12-16]。
密码分析根据攻击者掌握的信息分为唯密文、已知明文、选择明文和选择密文,其中,唯密文攻击要求攻击者获取的设备泄露信息最少,更容易实施,因此密码算法安全性的最低要求即是面对唯密文攻击的安全性。目前,针对LEA密码的分析均为传统密码分析和差分故障分析,攻击假设为选择明文和已知明文攻击,未有唯密文假设的攻击方法。
2013年Fuhr等[16]提出基于唯密文假设的故障分析,该方法仅利用任意错误密文和故障注入,可以实现密码算法的破译。唯密文故障分析已有研究对象包括具有SPN结构的AES密码、LED密码,以及具有Feistel结构的Piccolo密码等,未有ARX结构密码的相关分析结果。
本文针对具有ARX结构的LEA密码算法进行安全性分析,不仅完成了唯密文故障分析方法的密码破译,而且提出了比例距离单重区分器和比例距离-汉明重量、比例距离-极大似然双重区分器,降低了攻击所需的故障数量和时间。研究结果可为其他ARX结构密码的安全实现提供参考。
1 相关工作
近年来,国内外学者对LEA密码进行了安全性研究。2014年,Park等[10]提出了针对LEA密码的差分故障分析方法,使用300个故障恢复了算法的完整密钥。2015年,Jap等[11]采用随机比特翻转模型对LEA密码进行差分故障分析,降低了所需故障的数量。2016年,Song等[9]提出针对LEA密码的自动差分分析方法,对14轮的LEA密码进行了差分分析,提高了差分概率并降低了搜索时间。同年,Zhang等[7]评估了LEA密码对抗零相关线性分析的能力,完成了对9轮LEA密码的攻击。2020年,李航等[8]实现了对10轮LEA密码的积分攻击,计算复杂度为2120次。表1列举了针对LEA密码的多种分析结果。
2013年,Fuhr等[16]提出基于唯密文攻击假设的故障分析方法,将其应用于AES密码,利用受故障影响的中间状态的分布特性破解密钥,并提出平方欧氏不平衡、汉明重量和极大似然区分器。2016年,Dobraunig等[17]实现了对基于AES密码的认证加密算法的唯密文故障分析,并能够在多种微型设备上利用激光和时钟毛刺成功进行故障注入。此后,Li等[18]和李玮等[19]结合LED、Piccolo等密码提出了拟合优度、拟合优度-平方欧氏不平衡、拟合优度-极大似然和拟合优度-汉明重量等区分器,适用于SPN和Feistel结构密码的安全性分析。针对密钥长度为128 bit版本的AES、LED、Piccoco和LEA密码的攻击效果如表2所示。

表2 AES、LED、Piccolo和LEA密码恢复原始密钥所需故障数量的比较
2 LEA密码简介
2.1 符号说明
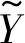
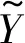
记r为总轮数;
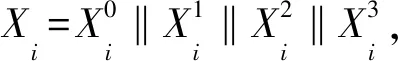
记K为原始密钥,由4个32 bit数据块组成,即K=K0‖K1‖K2‖K3;
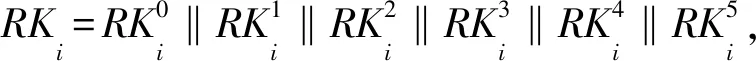
记∑为连加操作,Π为连乘操作。
2.2 算法描述
LEA密码是ARX结构密码,其分组长度为128 bit,密钥长度为128、192和256 bit,轮数分别为24、28和32。加解密过程和密钥编排方案仅采用模加、异或和移位操作,一轮结构图如图1所示。

图1 LEA密码算法轮函数结构图Fig.1 Round function of LEA
本文采用128bit密钥长度的LEA密码为分析对象。算法1给出了该版本的加密算法。解密算法以相反的子密钥使用顺序和模减操作实现,与加密算法结构类似。
算法1LEA密码加密算法
输入:X,RK0,RK1,…,RKi-1,r;
输出:Y。
①X0‖X1‖X2‖X3=X;
②U=X;
③U0‖U1‖U2‖U3=U;
④ fori= 0 tor-1 do
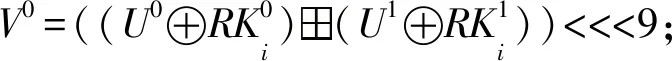

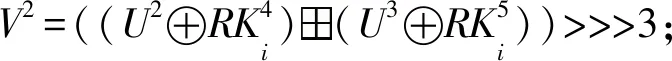
⑧V3=U0;
⑨V=V0‖V1‖V2‖V3;
⑩U=V;
2.3 密钥编排方案
LEA密码的密钥编排方案如算法2所示,其中,常数δ参照文献[6]。
算法2LEA密码密钥编排方案
输入:K0‖K1‖K2‖K3=K,δ,r;
输出:RK0,RK1,…,RKr-1。
①T0‖T1‖T2‖T3=K0‖K1‖K2‖K3;
② fori=0 tor-1 do
③T0=(T0(δimod4<< ④T1=(T1(δimod4<<<(i+1)))<<<3; ⑤T2=(T2(δimod4<<<(i+2)))<<<6; ⑥T3=(T3(δimod4<<<(i+3)))<<<11; ⑦RKi=T0‖T1‖T2‖T1‖T3‖T1; ⑧ end for ⑨ returnRK0,RK1,…,RKr-1。 本文采用随机单字节的故障模型,并基于唯密文假设对LEA密码进行分析。攻击者能够在加密过程中对设备注入单字节故障,以“与”运算的形式作用于中间状态。此后,攻击者仅能获取加密产生的随机密文。由于“与”运算的特点,所影响的中间状态中每个比特的均匀性被打破,因此故障注入后,单比特变化的概率情况如表3所示,在破译过程中利用了单比特分布的不均匀性质。 表3 经故障注入后的单比特分布概率 LEA密码的唯密文故障分析具体步骤如下: 图2 在第23轮注入单字节故障后的故障传播路径Fig.2 Fault propagation path of an 8-bit fault in the 23rd round (δ0<<<3)) 本文使用7种区分器对LEA密码进行唯密文故障分析,包括已有的平方欧氏不平衡、汉明重量、极大似然和拟合优度区分器,以及本文提出的比例距离、比例距离-汉明重量和比例距离-极大似然新型区分器。 3.3.1 现有区分器 (1)平方欧氏不平衡区分器。平方欧氏不平衡(square Euclidean imbalance,SEI)区分器用于衡量总体分布与均匀分布的差距[16]。由于注入故障后的比特服从的统计分布远离均匀分布,故当候选密钥的区分值最大时,该候选密钥为正确密钥的可能性也达到最大。SEI值可表示为 式中:n为导入的故障数量;Om为中间状态值中值为m的个数,m∈{0,1}。 (2)汉明重量区分器。汉明重量(Hamming weight,HW)区分器用于统计总体分布与零的距离[16]。汉明重量区分器计算的是一组中间状态值的平均汉明重量,由于理论分布中汉明重量与零的距离越近的值出现概率越大,故使得HW值最小的候选密钥为正确密钥的可能性最大。HW值可表示为 式中:n为导入的故障数量;h(·)为汉明重量值的计算函数;sν为第v个中间状态值;Om为中间状态值中值为m的个数,m∈{0,1}。 (3)极大似然区分器。极大似然(maximum likelihood,ML)区分器使用中间状态值的联合分布率作为候选密钥的指标,ML值越大,该候选密钥为正确密钥的可能性越大[16]。ML值可表示为 式中:n为导入的故障数量;sv为第v个中间状态值,Dsv为中间状态值为sv的理论概率;Dm为中间状态值为m的理论概率;Om为中间状态值中值为m的个数,m∈{0,1}。 (4)拟合优度区分器。拟合优度(goodness of fit,GF)区分器能判断已知样本分布率与理论分布率的拟合程度,正确密钥对应的样本分布与理论分布拟合程度最大[18]。GF值可表示为 式中:Om为中间状态值中值为m的个数;Rm为中间状态值为m的理论个数,m∈{0,1}。 3.3.2 新型区分器 (1)比例距离区分器。比例距离(ratio distance,RD)区分器统计单比特中间状态为“0”的数量和为“1”的数量的比值,根据分布的不均匀性选择与“1”距离最远的一组分布,即RD值最大的一组中间状态对应的候选密钥即为正确密钥。RD值可表示为 式中:O0、O1分别为中间状态值中值为“0”和“1”的数量。 (2)比例距离-汉明重量区分器。比例距离-汉明重量(RD-HW)区分器在RD区分器的基础上进行了改进,使用HW区分器可进一步提高正确密钥的筛选能力,通过赋予权重来计算两个单区分器的合并值,从而筛选出最小合并值所对应的正确密钥。RD-HW值可表示为 RD-HW值=w0·RD值+w1·HW值 式中:w0、w1分别为RD值和HW值的权重,w0+w1=1。 (3)比例距离-极大似然区分器。比例距离-极大似然(RD-ML)区分器结合了RD区分器和ML区分器的优势,对一组中间状态分别求出两者的区分器值,再通过权重分配,计算合计的区分器值,最终最大的合计区分器值所对应的候选密钥即为正确密钥。RD-ML值可表示为 RD-ML值=w0·RD值+w1·ML值 本试验部署并运行于云计算服务器(Intel Core Processor (Broadwell, no TSX, IBRS), Ubuntu 21.04, 2.4GHz),采用C++编程语言模拟试验。攻击者生成随机单字节故障,使用“与”操作将故障注入在指定位置,使中间状态值产生错误,并收集产生的故障密文。使用SEI、HW、ML、GF、RD、RD-HW和RD-ML区分器进行分析,并统计了恢复原始密钥的成功率、故障数量和耗时。 成功率是指故障分析者成功恢复原始密钥的概率。由于待统计的中间状态信息仅为单比特,即只有“0”和“1”两种情况,且所有操作均为模加、循环移位和异或操作,因此,多个密钥候选值会对应至同一中间状态,得到的候选密钥非唯一。由SEI区分器的原理可知,交换中间状态值中“0”与“1”的个数不改变SEI值大小,同时异或操作正是这种仅改变映射关系的变换,因此若最终的中间状态值通过与候选密钥块直接异或所得,则SEI区分器将无法起到区分效果。本试验成功率计入包括正确密钥的候选密钥集合,元素个数不超过8个。在不同区分器下恢复LEA密码的128 bit原始密钥的成功率随故障注入数量的变化如图3所示。 图3 各区分器恢复LEA密码的原始密钥的成功率随故障注入数量的变化Fig.3 The success rate of each distinguisher to recover the secret key of LEA with the number of faults injected 从图3可以看出,HW、ML、GF、RD、RD-HW和RD-ML区分器均可达99%及以上的成功率恢复LEA密码原始密钥,且新型区分器RD-ML、RD-HW和RD的成功率率先达99%,SEI区分器无法对候选密钥进行有效分析。 故障数量是衡量故障分析的主要指标,攻击者所需的故障数越少,在实际物联网环境下进行分析时越具有优势。在恢复LEA密码原始密钥的成功率达99%及以上时,各区分器所需的故障注入数量如表4所示。由表4可知,新型区分器RD、RD-HW和RD-ML所需故障数较少,其中,RD-ML区分器所需故障数最少。 表4 各区分器恢复LEA密码密钥所需的故障数量 耗时是密码算法攻击中的一个衡量指标。在使用不同区分器恢复LEA密码原始密钥的过程中,攻击者以99%及以上成功率恢复LEA密码原始密钥,耗时与注入故障数量的关系如图4所示。 图4 各区分器恢复LEA密码原始密钥的耗时随故障注入数量的变化Fig.4 The time of each distinguisher to recover the secret key ofLEA with the number of faults injected 耗时主要由遍历所有故障密文和候选密钥、反向推导中间状态值、统计中间状态值的分布情况、利用区分器筛选正确的密钥等所需的时间组成。试验结果表明,除SEI区分器外,其他区分器按耗时递减依次排序为RD-HW、RD-ML、ML、HW、GF和RD,所需的时间分别为0.771、0.745、0.174、0.142和0.139和0.133 ms,对应的故障数量为400、396、468、456、480和452个。由图4可知,单区分器的耗时少于双重区分器,新型单区分器RD耗时最少。 本文提出了针对LEA轻量级分组密码的唯密文故障分析方法,使用了比例距离、比例距离-汉明重量和比例距离-极大似然等新型区分器,在恢复LEA密码原始密钥的过程中攻击者降低了所需故障数量。研究结果表明,LEA密码无法抵御唯密文故障攻击。因此,建议使用者在物联网设备中使用该密码算法时,对密码设备进行必要的安全防护,以降低其遭受故障攻击威胁的程度。3 LEA密码的唯密文故障分析
3.1 基本假设和故障模型

3.2 攻击过程
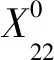


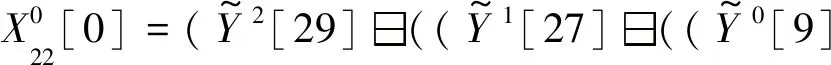
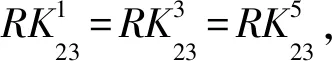
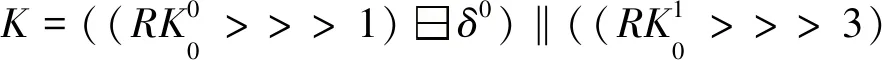


3.3 区分器


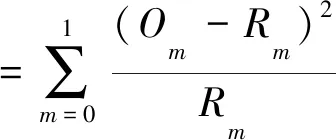
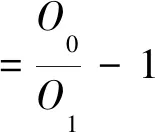
4 试验分析
4.1 成功率

4.2 故障数量

4.3 耗时

5 结 语

