基于随机森林算法的小样本纱线质量预测

刘智玉，陈南梁，汪 军，b

(东华大学 a.纺织学院, b.纺织面料技术教育部重点实验室, 上海 201620)

在纺织产业链中,纱线生产既是源头也是关键环节之一,其对后道加工的成本和效率以及最终纺织品的内在质量都有较大影响。因此,如何应用新技术实现快速的纱线质量预测,始终是纺织领域的重要研究内容之一。纱线质量的预测是非常复杂且困难的,因为它包含了太多不确定因素。国内外关于纱线质量预测的方法主要包括数理统计方法、灰色理论方法和机器学习方法。从20世纪90年代开始,研究人员尝试使用神经网络、支持向量机等机器学习算法进行纱线质量预测,其中基于神经网络算法及其优化方法的纱线质量预测得到较多的研究[1-3]。

然而,目前尚未有纱线质量预测相关研究成果实现实践应用,这主要是因为有两个比较突出的问题尚待解决。首先,预测模型的泛化能力具有局限性,这一点极大地限制了预测模型在实践中的适用性。泛化能力是指机器学习算法对新鲜样本的适应能力,即对于具有相同分布规律训练集以外的数据,预测模型也能做出正确判断。其次,市场需求越来越向小批量多品种的状况转变,且目前纺纱企业的数字化程度较低,因此在多数情况下,一个产品仅包含有限的小样本数据。而神经网络算法模型的本质是对复杂映射的拟合,其精度与待拟合映射的复杂度密切相关,严重依赖样本品质和样本量,在小样本学习中很难解决过拟合的问题。而纱线样本兼具映射复杂性及小样本的情况,使得基于神经网络算法的纱线质量预测模型常出现预测精度不稳定的问题[4-6]。

为改善上述问题,目前很多研究采用将神经网络算法和其他算法相结合的方法对神经网络算法进行优化,对单一试验样本的预测精度的提高取得一定效果[7-9]。但是,对预测模型面对不同样本集时的泛化能力和预测稳定性鲜有针对性研究。

本文针对当前基于神经网络算法的小样本纱线质量预测模型存在的典型问题,运用随机森林算法建立纱线质量预测模型,并将该模型与线性回归算法模型和多层感知机(multi-layer perceptron, MLP)神经网络算法模型进行对比,经过验证,发现随机森林算法在解决预测模型的泛化局限性和预测精度不稳定等方面显示出一定的优势。

1 预测模型与数据源

1.1 预测模型的建立

随机森林(random forest,RF)算法是2001年由Breiman[10]将Bagging集成学习理论与随机子空间方法相结合提出的一种机器学习算法,是利用多棵决策树对样本进行训练并预测的一种学习器,其模型框架如图1所示。

图1 随机森林算法模型框架Fig.1 Model framework of random forest algorithm

从图1可以看出,随机森林算法模型框架的构建过程主要由3个方面构成,即训练集的生成、决策树的构建和算法的产生。若要构建一个规模为N的随机森林,就需要有N颗树和N组训练集。在构建过程中,随机森林里有两个随机化:

(1)样本Bagging。从原样本集中通过bootstrvap自主采样,有放回地随机抽取N个与原样本集同样大小的训练样本集,然后基于这个新创建的数据集来构造决策树。

(2)特征的随机子空间。在对决策树每个节点进行分裂时,从全部M个特征中随机抽取一个特征子集,然后从这个子集中选择一个最优分裂特征来建树。在特征空间的不同子空间上训练各决策树,以略微增加偏差为代价减少过拟合问题,从而使随机森林能较好地容忍噪声,并且具有较好的泛化性能,对异常噪声具有较好的稳健性。

在构建每个决策树时,随机抽取训练样本集和特征子集的过程都是独立的,且总体都是一样的,因此,{θn,n=1,2,…,N}是一个独立同分布的随机变量序列。由于各个决策树的训练是相互独立的,因此,通过并行处理来实现随机森林的训练。

随机森林算法理论决定了其优缺点。随机森林算法有诸多优点,如:可适用于特征很多的数据,不需要降维,以及不需要做特征选择;可以输出特征的重要性排序,方便逻辑解释;不容易过拟合,能较好地容忍噪声,具有较好的泛化性能,对异常噪声具有较好的稳健性等[11-13]。随机森林算法在用于大样本时计算成本较大,训练和预测的速度略慢,一般使用多核处理器并行计算并增大内存的方法缓解此问题;随机森林算法在用于小样本时几乎不受此干扰,训练和预测速度都较快。

目前随机森林算法在金融学、医学、生物学等众多领域已取得较好的应用[14-15],但在纺织领域尚未见相关研究报道。

本文建立的用于小样本纱线质量预测的随机森林算法模型,所用的编程语言为Python,算法基于scikit-learn库实现。

1.2 数据源

本文引用文献[1]中表1所示的数据,共60条样本数据,将4个棉纤维质量指标作为特征因子(输入因子),2个纱线质量指标作为输出因子。

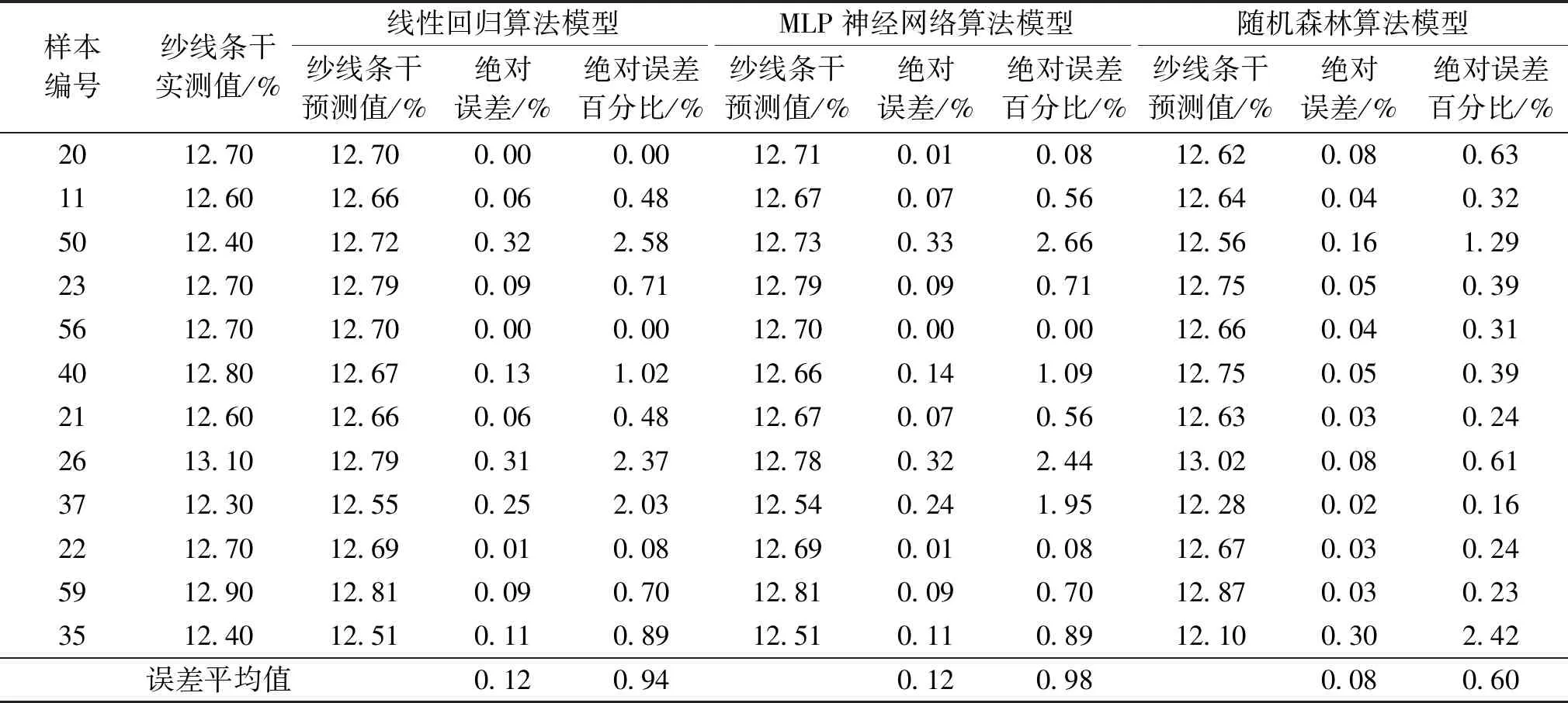
表1 纱线条干预测结果Table 1 Prediction results of yarn evenness

表2 纱线强度预测结果Table 2 Prediction results of yarn strength

2 模型的评估方法

2.1 模型预测精度的评估

模型预测精度的评价指标包括:预测结果的决定系数(coefficient of determination,即Score值)、均方根误差(root mean square error,RMSE)、绝对误差平均值(mean absolute error,MAE)、绝对误差百分比平均值(mean absolute percentage error,MAPE),计算公式如下:

(1)

(2)

(3)

(4)

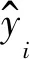
2.2 模型泛化能力的评估

本文通过交叉验证(cross validation,CV)来评估模型的泛化能力。交叉验证是在样本量有限的情况下有效评估模型性能的一种方法。交叉验证有多种实现方法,本文选用K折交叉验证方法进行模型评估。

K折交叉验证(Kfold cross validation)是将整个样本数据集划分为K个相等大小的部分,每个部分被称为一个“折”(fold)。选其中1折用作验证集,其余K-1折用作训练集。重复K次,将所有数据都遍历一次。模型的最终精度是通过取K次验证的平均精度来计算的。

K折交叉的取样方式使得其训练集和验证集会受到样本排列顺序的影响,从而验证集中数据特征与训练集数据特征不同的概率大大增加,因此,当遇到离群值或未知特征的数据(即与训练数据具有明显不同特征的测试数据)时,可在一定程度上模拟预测模型潜在的泛化能力。

3 试验与分析

采用网格搜索(grid search)的方法对scikit-learn库的RandomForestRegressor回归器进行参数优选,最终建立本文试验用随机森林算法模型。

本文还建立了多层感知机MLP神经网络算法模型和线性回归算法模型,用作以下试验中的对比模型。其中:MLP神经网络算法模型作为随机森林算法模型的性能差异对比模型;线性回归算法模型作为一个稳固的对比基准模型,因为其不像其他需要调参的算法模型(包括神经网络算法模型、随机森林算法模型等),模型性能不会受到不同参数选择的影响。

常规预测试验所用的训练集和测试集是运用scikit-learn库中的train_test_split()函数从总样本集中随机抽样得到的,而交叉验证中的训练集和测试集为固定分段得到的,在这里又被称为固定样本集。

在常规预测试验中,直接采用所建立的随机森林算法模型、MLP神经网络算法模型和线性回归算法模型进行预测试验。在交叉验证试验中,应用scikit-learn库中的cross_val_score()函数对各算法模型进行验证。

3.1 常规预测试验分析

将train_test_split()函数的test_size参数设置为0.20,即从样本集中随机抽取48个样本作为训练集、12个样本作为测试集,分别用3种算法模型进行纱线条干和强度的常规预测试验,预测结果如表1和2所示。

从表1和2可以看出,3种模型的纱线条干和强度预测值与实测值之间的绝对误差百分比平均值都小于1%,由此说明模型的精度较好,证明了本文所建3种预测模型的有效性。

3种算法模型常规预测结果对两个输出因子的总的Score值、MAE、RMSE如表3所示。从表3可以看出:随机森林算法模型的Score值最高,MLP神经网络算法模型次之,线性回归算法模型最低;相应地,随机森林算法模型的MAE和RMSE最小,MLP神经网络算法模型次之,线性回归算法模型最高。由此表明,随机森林算法模型的预测精度最高,MLP神经网络算法模型次之,线性回归算法模型最低。

表3 3种算法模型常规预测的预测性能对比表

3.2 各算法模型的预测性能对样本量敏感性的试验分析

众所周知,训练样本量的大小会对模型的预测效果产生影响,尤其对于小样本数据集而言,这个问题更加凸显。本文采用不同test_size参数进行多次常规预测试验,以检验各算法模型的预测性能对样本量的敏感性。其中,test_size参数取值范围为0.10～0.50,步长为0.05。总样本量为60不变,则训练样本量和测试样本量随test_size参数取值相应变化。3种算法模型在不同的test_size参数设置时的预测结果Score值、MAE、RMSE如图2所示。

由图2(a)可知,随着test_size参数的增大,训练样本量减少,各算法模型的预测结果的Score值总体呈下降趋势,符合训练样本量减少对预测性能影响的常规经验。其中,当test_size 参数大于 0.35后,即训练样本小于39个后,3个算法模型的训练精度都开始明显下降。可以认为,本试验中的最小有效训练样本量为39个。需要注意的是,因为实践中各种不同数据集具有不同的数据特征,因此没有关于不同算法模型对训练样本量的敏感程度的普适性的定量经验,对于小样本数据集,尤其如此。

从图2(a)中还可以看出,当test_size参数设置过小时,各算法模型的预测效果也会受到一定程度的影响。如本试验中当test_size参数等于0.10时,3种算法模型的预测结果的Score值都不是各自曲线的最高点。当test_size参数等于0.15时,MLP神经网络算法模型的预测结果的Score值甚至明显降低。这主要是因为针对固定样本集,当训练样本量增大时,意味着测试样本量减小。当测试样本量过小时,如果测试样本中存在离群值,则离群值对整个测试集的平均预测精度的影响会凸显出来。当test_size参数设置为0.20时,线性回归算法模型和MLP神经网络算法模型的预测结果的Score值基本处于最高水平,随机森林算法模型的预测结果的Score值虽然不是其曲线中最高点,但是也处在一个相对高位。由此可见,在面对一个固定样本量的数据集时,训练样本和测试样本的分配比例会对预测精度造成影响。

从图2可以看出,在各种test_size参数下,3种算法模型中随机森林算法模型预测结果的Score值都是最高的,MAE和RMSE都是最低的。MLP神经网络算法模型预测结果的Score值随训练样本量变化波动最大,且多数情况下其MAE和RMSE最高。由此表明,MLP神经网络算法对样本量的敏感度最大,在面对小样本量时其预测精度稳定性的问题最突出,而随机森林算法模型在不同样本量情况下的预测准确性和稳定性都是最好的。

3.3 交叉验证试验分析

对3种算法模型分别采用3折、4折、5折、6折交叉验证,以检验模型的泛化能力。当test_size参数等于0.20时,3种算法模型的常规预测的Score值与各折数的K折交叉验证的Score值的对比如图3所示。

图3 3种算法模型的常规预测与K折交叉验证的Score值Fig.3 Score values of conventional prediction and K fold cross-validation of three algorithm models

从图3可以看出,常规预测的Score值明显大于K折交叉验证的Score值。因为常规预测通过随机抽样,增加了训练样本的丰富性,使得各算法模型对本文所用样本集呈现出更高的预测水平,而K折交叉验证按顺序逐折(fold)取样因此受到样本排列顺序的影响。K折交叉验证更接近于模拟各算法模型在纱线实际生产中应用时面对新样本集时可能呈现的预测性能,更能考察算法模型的泛化能力。

在图3中,各算法模型的K折交叉验证的Score值几乎均随着折数增加而降低。因为随着折数增加,每次验证时的测试样本量减少,当遇到离群点时,离群点在测试样本中的占比增大,从而影响预测结果的平均精度。

对比图3中常规预测和不同K折交叉验证的预测结果的Score值可发现,K折交叉验证时线性回归算法模型和MLP神经网络算法模型的预测性能大幅下降,但随机森林模型的预测性能下降较小。以3折交叉验证为例,相对于常规预测,线性回归算法模型、MLP神经网络算法模型、随机森林算法模型的Score值分别下降了24.3%、23.9%、4.9%。由此可见,对固定样本集展现了良好预测性能的算法模型,如果其泛化能力弱,则在面对实际生产中的新数据时可能会出现预测性能大幅降低的情况。其原因是泛化能力弱的算法模型会过于拟合所选的固定样本集中训练数据的细节,从而造成过拟合。

由此可见,在进行不同算法模型的性能对比以及对某一算法模型的不同参数进行择优时,应尽量采用动态数据集,如果使用固定数据集,不能仅采用单次常规预测的Score值作为评判依据,还应同时采用K折交叉验证的Score值作为评判依据,以便对算法模型和所选参数做出更全面的评价。

在图3中的各种折数的交叉验证中,随机森林算法模型的Score值均明显大于其他两种算法模型,并且随着折数增加,随机森林算法模型的Score值下降幅度最小。对比Score值变化差异最大的3折和6折交叉验证发现,线性回归算法模型、MLP神经网络算法模型、随机森林算法模型的Score值分别下降了27.2%,29.7%,13.7%。

由此可见,在本试验中,随机森林算法模型的泛化能力和预测稳定性均优于线性回归算法模型和MLP神经网络算法模型。

3种算法模型分别在3折、4折、5折、6折交叉验证中的每一折的预测Score值如图4所示。从图4可以看出,在各种折数的交叉验证中,3种算法模型的Score值曲线的波动趋势大体吻合,证明Score值曲线中的大幅波动主要是由样本本身的变化引起的,而不是由算法引起的。

图4 3种算法模型的K折交叉验证中每一折的预测结果Score值曲线Fig.4 Score curves of each fold in K fold cross-validation of three algorithm models

在图4中,几乎在各种折数的K折交叉验证的每一折,随机森林算法模型的预测结果的Score值均明显占优。在5折和6折交叉验证的最后一折,线性回归算法模型和MLP神经网络算法模型的预测结果的Score值已经接近0甚至小于0,随机森林算法模型的预测结果的Score值仍能分别处于0.49和0.41的水平,再次说明随机森林算法模型的泛化能力更强、稳定性更好。

4 结 论

本文构建了基于随机森林算法的纱线质量预测模型,对小样本纱线数据集进行预测试验,将随机森林算法模型与线性回归算法模型和MLP神经网络算法模型进行对比,得出以下结论:

(1)所建立的随机森林算法模型、线性回归算法模型和MLP神经网络算法模型,在常规随机抽样预测中的预测结果的MAPE均在1%以内,由此证实了3个模型的有效性。

(2)在各种不同训练样本量的常规随机抽样试验中,随机森林算法模型的预测结果相比其他两种算法模型具有更高的Score值、更小的MAE值和RMSE值,前者预测精度更高。由此证明随机森林算法模型对小样本数据集的预测准确度更好。

(3)在多种折数的K折交叉验证试验中以及在对常规随机抽样预测与按试样排列顺序逐折取样的K折交叉验证试验的对比中,相比其他两种算法模型,随机森林算法模型的预测结果不仅呈现出更高的Score值,而且具有明显更小的Score值波动范围。由此证明随机森林算法模型的泛化能力和预测稳定性更好,其在生产实践预测中具有良好的应用潜力。