《概率论与数理统计》试卷质量分析

刘艳娜 刘敏 王瑞

在“以学生为中心”的现代教育理念中，考试的诊断性功能和发展性功能在不断强化。通过测量与评价，判断课程整体的教学效果，帮助测评者与被测评者尽快发现问题，及时调整与修正教学中存在的不足，可以达到以考促教、以考促学、以考促建的目的。

2017—2020年，我院《工程数学》课程使用试卷库随机抽题的形式进行课程终结考核。随着考核方式的优化，规范地、科学地开展教育测量与评价，挖掘并反馈数据关系中隐藏的大量教育信息，准确地把握学生对知识的掌握程度，对于后续课程的教学和考核评价工作具有重要的意义和价值，准确、科学的试卷质量评价工作使试卷库考核评价方式形成闭环。

一、试卷质量分析指标体系

根据教育测量学的理论，常用衡量试卷质量的检验指标主要有信度、效度、难度和区分度，即试卷的成绩能否反映学员的学习水平、考核内容能否反映教学重点、考核难度是否适中、学员水平是否能区分等，下面分别说明四个指标的含义和计算方法。

（一）信度

信度即测验结果的可信程度，它是反映测验结果的一致性、可靠性和稳定性的指标。常用的信度系数有三种：再测信度系数、复本信度系数、内部一致性系数。内部一致性系数是反映一个测验中被测各题所得分数的一致性指标，可用来估计测验内部一致性信度，常用的内部一致性系数有分半信度系数、库德—理查逊系数和克伦巴赫系数三种。针对不同的测验可使用以上三种方法中的一种。

（二）效度

效度是指测验结果的有效程度。通俗地说，效度是度量测验是否达到了预期目的的指标，是评鉴测验质量的重要指标。效度是教育测量中最基本也是最重要的问题。根据不同的角度，可将效度分为不同的类型，按照测验目标对效度进行分类：内容效度、构想效度和效标关联效度、结果效度。内容效度是指测验内容与预定要测的内容之间的一致程度，它反映了测验题目在所要测量的内容范围和教学目标内取样是否充分和确切的问题，主要用于学科成绩测验。内容效度的评估方法分为定性分析和定量分析两种。定性分析的方法为专家判断法。定量分析的统计分析法有：克伦巴赫法、前后测对比法、评分一致性考查法。

（三）难度

难度是指测验题目的难易程度，一般以能够正确回答试题的人数与参加测验的总人数之比作为难度指标。测验试题的难度可以反映出被测者的能力水平能否得到真实的体现，因而恰当的难度是一个好的测验的重要质量指标。

（四）区分度

区分度是指试题对不同考生的知识、能力水平的鉴别程度。计算区分度的方法有：极端分组法和相关法。

二、试卷质量分析指标等级判定

以2017年《概率论与数理统计》试卷为例说明分析过程，其他年份方法相同。首先使用SPSS软件对考核结果进行描述性统计分析。

（一）试卷成绩的频率直方图和箱线图

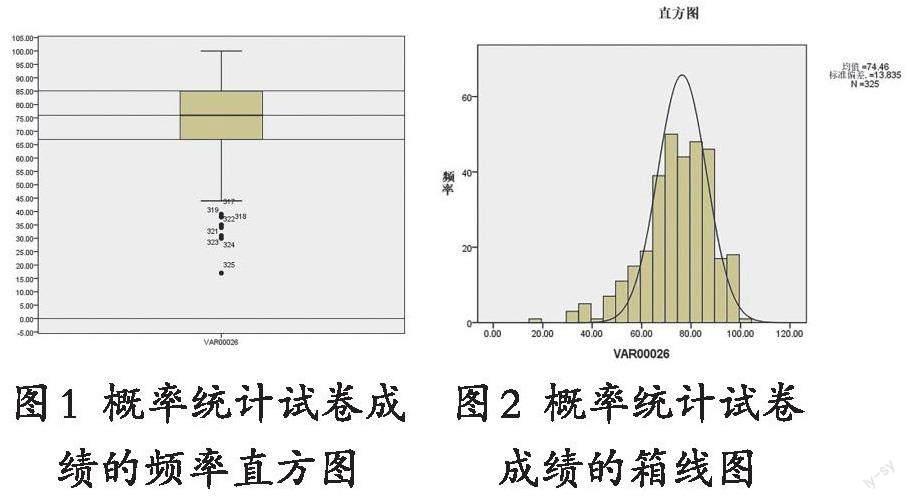
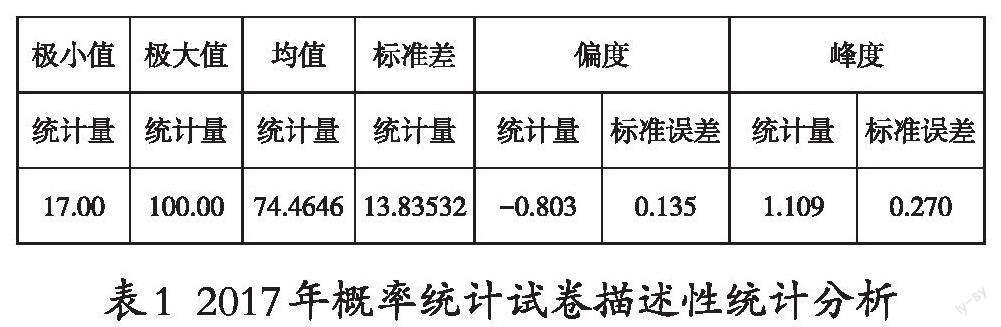
为了直观反映学员的成绩分布情况，绘制成绩的频率直方图和箱线图，如图1、图2所示。

由圖1频率直方图可以看到：成绩有一个峰，中间高、两头低，比较对称，接近正态分布，可进行正态分布的检验。箱线图是基于最小值、第一四分位数、中位数、第三四分位数、最大值以上5个数的图形概括，图上标出了第一四分位数67、中位数76、第三四分位数85三条数值线。

从图2箱线图中，我们可以看到：箱线图从最小值到最大值被分成四个区间，区间的长短反映了成绩的集中程度，即区间越短说明成绩落在该区间比较集中，说明学员成绩不存在两极分化的现象。箱线图中位数所在的位置就是数据集的中心，若中位数位于箱子的中间位置，则数据分布较为对称。另外，最小值与中位数的距离比最大值与中位数的距离大，说明成绩的数据分布向左倾斜，由频率直方图也可以发现此规律。将成绩低于45分的标为离群点，并在图上可以看到对应的编号。

（二）试卷成绩的描述性统计分析

2017年《概率论与数理统计》结课试卷成绩的描述性统计分析见表1。

表1 2017年概率统计试卷描述性统计分析

标准差：学生成绩的标准差一般在满分的5%—10%以内是正常的，即100分试题的标准差为5—10分是合理的。经计算2017年试卷的标准差为13.84分，成绩离散度比较大，说明学员两极分化的情况比较严重，例如最低分17分，与平均分相距过大导致。

偏度值：描述数据分布的对称性。经计算偏度值为-0.803，说明大部分学员的成绩集中于平均分左侧，即学员成绩小于平均分的人数略多于高于平均分的人，属于负偏态分布。正态分布是一种不作任何教学要求的成绩的随机分布，教师期待的学生成绩分布不应该是正态分布。对于有教学目标、有教学要求的教学，学生成绩的频率呈负偏态分布是更期望的结果。

峰度值：描述数据围绕平均分分布的紧密程度。经计算峰度值为1.109，属于低峰态，成绩中间部分的少，两端人数相对较多，属于两极分化。

（三）试卷信度分析

分半信度系数是将一个测验分成两个等值且独立的部分，如按照奇数、偶数将试题分成两部分。分组之后，求两部分得分的积差相关系数，即分半信度系数。由于计算题共九道大题，为了使分类后两组试题分数和相同，舍去最后一道大题，每组有十道题目，对分好后的两组得分数据进行分半信度系数的计算。首先计算每一名学生的奇数题总分和偶数题总分；其次由积差相关系数公式计算分类的两组题目的相关系数作为分半信度系数rxy=0.58；最后使用斯皮尔曼—布朗公式校正分半信度系数得到矫正后的信度系数r=0.735。信度是测验中随机误差大小的反映，试卷信度大于0.5为宜，故该试卷测得的分数具有较高的可靠性。

（四）试卷效度分析

计算试卷的效度采用计算克伦巴赫系数的方法。克伦巴赫法通过计算克伦巴赫系数a来判别测验的内容效度。克伦巴赫认为，内容效度可由一组被测在测验试卷的两个等值复本上得分的相关系数来表示。当相关系数较高时，可以推断测验具有较高的内容效度；当相关系数较低时，则说明测验的内容效度较低。经计算本套试卷的克伦巴赫系数为0.713，可见试卷内容具有较高的效度。效度是对测验中系统误差大小的反映，是对测试所要研究的问题而言，检验测试是否测量了想测量的知识和技能，主要回答测量工具是否合适，即测试结果的正确性问题。

（五）试卷难度分析

针对不同的题型类别计算试题难度的方法是不同的，一般的试题难度评判等级如下：极高（0.3以下），较高（0.3—0.6），中等（0.6—0.8），较低（0.8以上）。下面针对不同题型分别给出其计算方法。

二值记分题就是每个题目只有两种评分结果，比如选择题，答对记3分，不答或答错记0分，这些属于二值记分题。二值记分题的难度值计算公式为P=K/N；其中P为难度值，N为被测试的人数，K为答对该题目的人数。难度值P越大说明这道题越容易做，即难度越小。选择题第6小题难度值为0.425，级别属于较高。多值记分题的难度值计算方法：多值记分题至少有3种可能的记分结果，学科测试中的简答题、计算题论述题等都属于多值记分题。多值记分题的难度值计算公式为P=X/Xmax，其中P代表题目难度，X为被试在某题目上的平均得分，Xmax为该题目的满分。填空题、计算题4、5难度值接近较高的级别，计算题1、综合题1、2、3都属于中等难度的题目。整张试卷的平均分为74.46分，故试卷的难度值为0.7446，属于难度中等。

（六）试卷区分度分析

区分度计算方法也依据主观性试题和客观性试题具有不同的计算方法。一般的考试成绩的区分度评判等级如下：好（0.4—1），良好（0.3—0.4），尚可（0.2—0.3），差（0.2以下）。下面根据不同的题型给出其计算方法：

客观性试题的区分度计算公式D=PH-PL，其中D为区分度，PH为高分组通过率，PL为低分通过率。客观性试题（选择题）的区分度良好和好的题目有第5题和第6题。主观性试题的区分度计算公式：D=（XH-XL）/N（H-L），其中D為区分度，XH为高分组的总分，XL为低分组的总分，H为该试题的最高得分，L为该试题的最低得分，N为考生总人数的25%。主观题（填空题、计算题）区分度良好的题目有填空题和计算题1；区分度好的题目有计算题4、5，综合题2、3。最后，试卷客观题区分度为0.201，属于尚可等级；主观题区分度为0.356，属于良好等级；试卷的区分度为0.326，属于良好等级。

三、试卷质量分析的结论与启示

《概率论与数理统计》作为我院最早开始建设试题库的课程，2017年投入使用。笔者从四个维度对试卷的质量进行分析，得到以下的一些结论和启示：

（一）试卷质量的情况

表 2017—2020年概率统计试卷质量分析指标值

通过对试卷质量多项指标体系进行定量的计算，并依据评定标准对概率统计试卷的质量做出评定结论。由表可以看到，四年的试卷在效度、难度和区分度上都比较接近，并且其评定结论也比较理想，说明试卷达到了科学有效地评估学生学习成绩的目的。同时，为了突出试卷的诊断性和发展性功能，我们对试卷难度和区分度进行详细的分析和评估，并对难度较大、区分度较好的知识点进行了梳理，如一维随机变量的综合题、抽样分布判别参数、无偏性等知识点失分较多，针对每类失分较多的题目总结其原因有：综合性题目涉及多个知识点对分析能力有要求、如抽样分布等抽象概念学生存在原理理解困难的情况、无偏性等题目题型灵活要求学生逻辑推理能力等。

（二）注重核心概念和数学思想的考查

通过对四年试卷的题型进行分析，试卷的计算题和综合题侧重考查课程的基本方法和应用，试卷的选择题和计算题则侧重考查基本概念和基本理论。在题目内容的设计上，选择题和填空题虽然分值略少，但是一部分题目分量不小，很多核心概念和性质的考查非常细致，学生对于概念的掌握稍微模糊一点就会出错。在综合题中，试卷设计了考查学生对区间估计思想方法的题目，构造教材上没有给出的参数的置信区间。对于抽象性强的课程而言，学生能够理解并准确地使用数学语言描述问题、解决问题是考查的一个重点，因此对于核心概念和数学思想的考查应成为课程考核和试卷质量分析的关注点。

（三）增加应用问题的考查

当下，学生用数学解决问题的能力已经成为很多选拔性考试关注的焦点。数学应用意识是主体运用所获得的数学观点和方法，主动地从数学的角度观察事物，阐述现象，分析问题，用数学的语言、知识、思想方法描述、理解和解决各种问题。课程考核中，可以将应用性问题以大作业的形式作为形成性考核的内容，还可以设计数学实验，引导学生了解、使用数学计算平台进行数值模拟和计算，在实践中增加用数学解决实际问题的体验感，反过来对数学的继续学习起到引导作用。

（四）提倡开放性问题的考查

教师要鼓励学生一题多解，从不同的角度对问题进行分析与求解。一题多解要求学生对问题有深入的思考，对知识体系还要能够达到融会贯通的能力。

运用数理统计的方法分析试卷可以准确地掌握学员在知识学习中集中存在的问题，帮助教师准确掌握本班级的教学情况，发现学生在学习中存在的困难与问题，准确掌握学生学习的知识点盲区，包括对概念、定理和计算方面存在的不足等，从而及时对教学内容进行完善与优化，进而科学地制定、改进教学计划，提出改进策略。通过对试卷进行科学、规范地分析，还可以为试题库或试卷库的建设提供数据支撑，删除或替换区分度、效度不高的题目，提高试题库质量，达到有效合理使用教学测量与评价的目的。

（焦  佳）