基于Marshall-Olkin Alpha Power 耿贝尔II型分布的参数推断

程月,田茂再,2

（1.新疆财经大学统计与数据科学学院,新疆 乌鲁木齐 830012；2.中国人民大学应用统计科学研究中心,北京 100190）

统计分布被广泛用于分析和预测真实世界的现象,但由于新的应用程序和事件的快速出现,需要不断开发新的分布,因此统计分布理论和产生新的分布引起了人们极大的研究兴趣.近几年,研究者对极端事件的极端值在各个领域进行分析,尤其是在数学、医学以及统计学等领域.虽然Gumbel Type-II 分布已成为广义极值理论的重要组成部分,但与Weibull 分布不同的是该分布由于拟合欠佳而导致其应用的普及率较低.由于在现实生活实践中经常遇到较多复杂现象的危险率是非常单调的,因此不能用Gumbel Type-II 分布进行建模.相反,此分布仅应用于具有单调失效率的实际数据.

为了解决这一限制,目前国内外有很多关于Gumbel Type-II（GT-II）分布最新发展和应用的文献.Okorie 等[1]发现了具有三个参数的EG Type-2 分布,并利用一组实际数据展示了EG Type-2 分布在相比较的分布中具有最佳拟合；Ogunde 等[2]提出了一种新的四个参数的EGTT 分布并推出密度、次序统计量和矩目函数等表达式,最后采用猪的癌症缓解时间和生存时间两组生命数据证实EGTT 分布在建模真实生命数据中的适用性,进而发现EGTT 分布更加灵活；Sindhu 等[3]推广了一种GLET-GTII 分布以及一些特定的统计属性, 提出了运用贝叶斯估计和极大似然估计来讨论GLET-GTII 分布的参数估计,MCMC 模拟分析结果与估计量是一致的.最后收集了中国1 月23 日-3 月28 日和欧洲3 月1 日-3 月30 日因COVID-19 的死亡人数数据分析GLET-GTII 分布的适用性,使用经典的拟合优度指标评估GLET-GTII 分布优于绝大数已知的分布；袁丹华等[4]讨论了在逐次II 型截尾样本下的Gumbel 极值分布,分别利用Bayes 估计和IFM法对该分布进行参数估计,结果表明当参数偏离1 的程度较小时,这两种方法的估计出来的结果相差不大,但当参数偏离程度较大时,IFM方法的估计结果较差于Bayes 估计的结果；Sindhu 等[5]提出了一种具有三参数的ETGT-II 分布并分析了具体的统计属性以及相关测度、矩生成函数、生存函数、分位数函数等.最后为了检验ETGT-II 分布的有效性进行仿真分析,利用已有文献中收集的欧洲和中国因新冠肺炎死亡的人数数据验证了ETGT-II 分布相比其他分布具有较好的适用性；Willayat 等[6]提出了一种新的概率MOEGT-II 分布,它可以对各种形状的失效率函数进行建模,并利用MLE 方法对MOEGT-II 分布的未知参数进行估计,运用3 种不同的迭代方法对不同大小样本进行模拟研究,发现与估计量是一致的.最后选取三组实际数据集与GT-II、EGT-II、MOGT-II、Frechet 等分布进行比较分析,发现MOEGT-II 分布优于其他分布且更具有适用性；Lone 等[7]使用了一种新的概率分布族与Gumbel Type-II 分布建立了一个独特的NAPGT-II 分布,运用两组真实生活数据证明MAPGT-II 分布的P值最大,K-S 最低,比所对比的竞争分布产生了更好的拟合.本文主要使用MOAP 分布族与Gumbel Type-II 分布建立了一个新的分布,把这个新的分布命名为MOAPGT-II 分布.

1 理论方法

Marshall-Olkin 的分布家族是由Marshall 等[8]提出的一种新的方法,此方法增加一个形状参数到分布中.假设G（x）和g（x）作为给定随机变量X的累积分布函数（CDF）和概率密度函数（PDF）.则Marshall-Olkin家族的累积分布函数和概率密度函数分别为

Mahdavi 等[9]通过增加一个新参数α,以累积分布函数作为基线进行变换,从而获得更加灵活的分布族,由此提出了alpha power transform（APT）类的方法.假设G（x）是任何分布的累积分布函数,则APT类的累积分布函数和概率密度函数分别为

Nassar 等[10]在前面两位学者研究结果的基础上,提出了一种新的方法,将额外的参数引入到分布族中,以获得更大的灵活性,进而得到一个新的分布,定义为Marshall Olkin alpha power（MOAP）分布族,表示MOAP 分布族的累积分布函数和概率密度函数分别为

本文假定基线分布为参数γ 和δ 的Gumbel Type-II 分布的累积分布函数（CDF）和概率密度函数（PDF）如下

通过使用MOAP 分布族和Gumbel Type-II 分布生成具有4 参数的MOAPGT-II 分布,其中且≠1,则MOAPGT-II 分布的累积分布函数（CDF）和概率密度函数（PDF）如下

不同参数值下的MOAPGT-II 分布的概率密度图见图1.

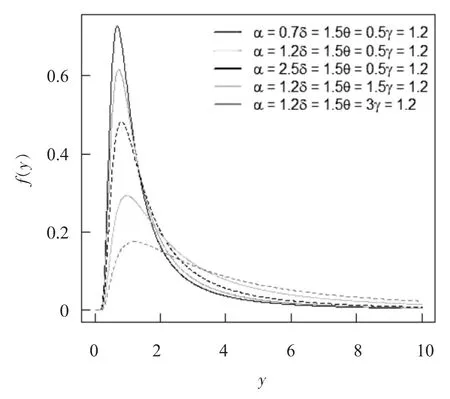
图1 不同参数值下的MOAPGT-II 分布的概率密度图Fig.1 Probability density diagram of MOAPGT-II distribution with different parameter values

在图1 中可以得到,在其他参数不变的情况下,随着参数α 的增大,控制了MOAPGT-II 分布函数从陡峭变为逐渐平缓的变化.

首先,生存函数又叫可靠性函数,它可以表示为一系列事件的随机变量函数,一般来说是用于表示一些基于时间的系统失败或死亡概率.采用公式来确定MOAPGT-II 分布的生存函数如下

不同参数值下的MOAPGT-II 分布的生存函数见图2.

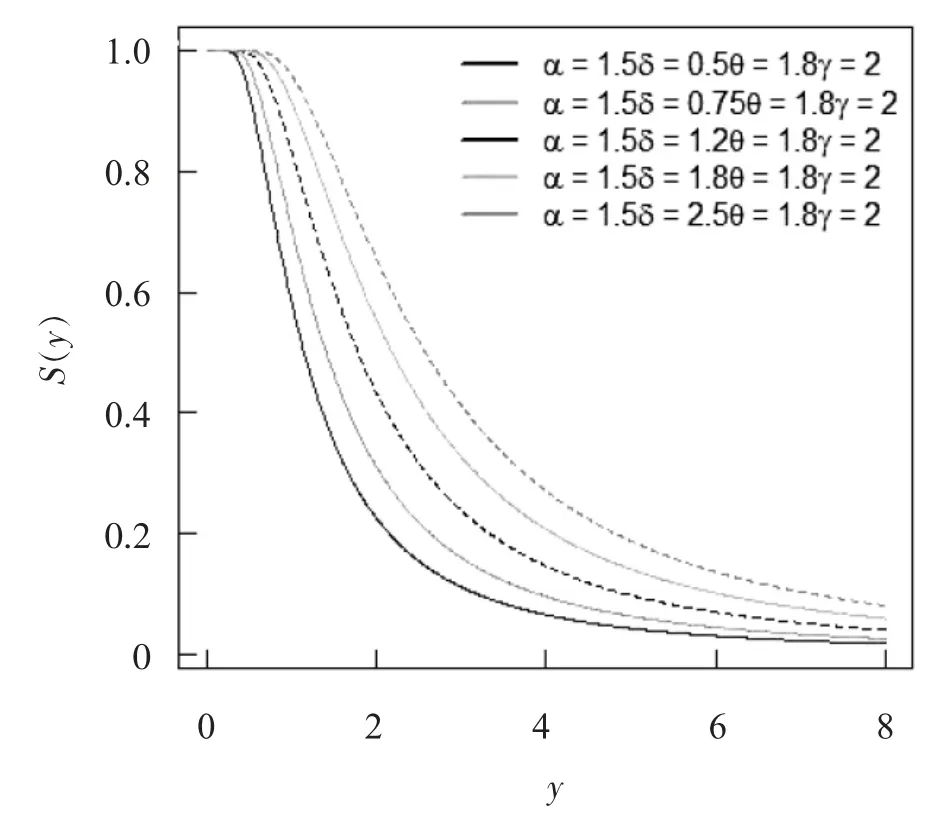
图2 不同参数值下的MOAPGT-II 分布的生存函数图Fig.2 The survival function diagram of MOAPGT-II distribution with different parameter values

其次,通过以下公式来确定MOAPGT-II 分布的风险函数为

不同参数值下的MOAPGT-II 分布的风险函数见图3.

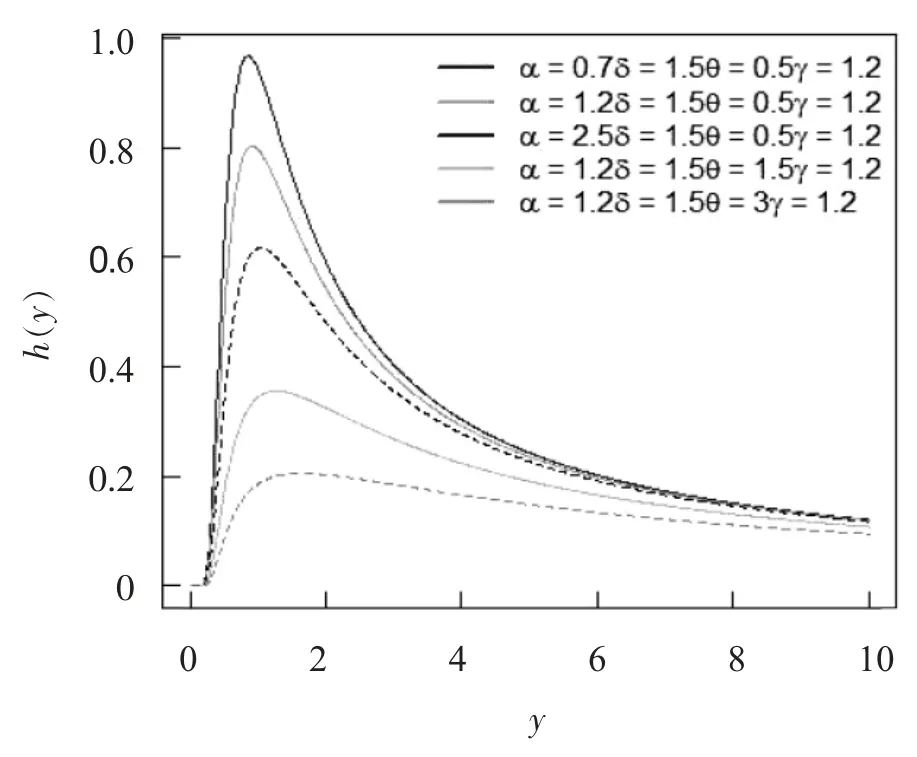
图3 不同参数值下的MOAPGT-II 分布的风险函数图Fig.3 The risk function diagram of MOAPGT-II distribution under different parameter values

紧接着通过公式（13）来确定MOAPGT-II 分布的反风险函数为

最后通过公式（14）来确定MOAPGT-II 分布的赔率比为

2 极大似然估计

在本节中,讨论使用R 语言编程来实现极大似然估计方法对所提出的MOAPGT-II 分布的参数进行估计.设y1,y2…,yn是样本总体Y1,Y2…,Yn的一个样本值,那么它的概率密度函数可以表示为f(yi,Ψ ),其中 Ψ为待估参数,可以计算出联合概率密度函数f(yi,Ψ )的似然函数为

对数似然函数的一般形式表示为

对（15）关于 Ψ求导有

lnL(Ψ )与L(Ψ )可以在同一点处取得极大值,因此 Ψ的极大似然估计值也可以从式（18）解得

采用极大似然方法对该分布的参数进行估计的主要步骤如下：

（1）由总体分布导出样本的联合概率密度函数

（2）把样本的联合概率密度函数中的自变量看成已知的参数,把待估参数 Ψ看作自变量,从而得到对数似然函数lnL(Ψ)

（3）求解出对数似然函数lnL(Ψ )的最大值点的 Ψ值

（4）将样本数据代入到式（19）的结果中,可以计算出参数的估计量.

一般来说,求解上面的非线性似然方程很难得到解析式,为了在数值上解决这些问题,需要采用牛顿法等迭代过程.因此本文使用optim（）R 函数执行,参数方法=“L-BFGSB”.执行后,分别以数字形式和视觉形式展示所获得的结果.

MOAPGT-II 分布的模拟是通过选择随机样本来实现的,利用模拟研究了MLE 相对于样本大小n的性能,遵循以下步骤进行数值模拟分析：设Yi,i=1,2,… ,n是来自MOAPGT-II分布模型式（10）中的独立分布的样本,估计程序生成的样本量n 分别为50、100、200、400、600、800和1000,这些样本是通过逆分布函数获得的,设定整个估计程序的模拟次数m=1 000 次.最后考虑使用平均偏差（Bias）和均方误差（MSE）作为评价标准,其中是Ψ的估计值,则二者公式分别表示为

表1 中展示了MOAPGT-II 分布参数α、δ、θ和γ的初始值分别设置为1.05、0.1、1.6、4 的情况下的估计结果.

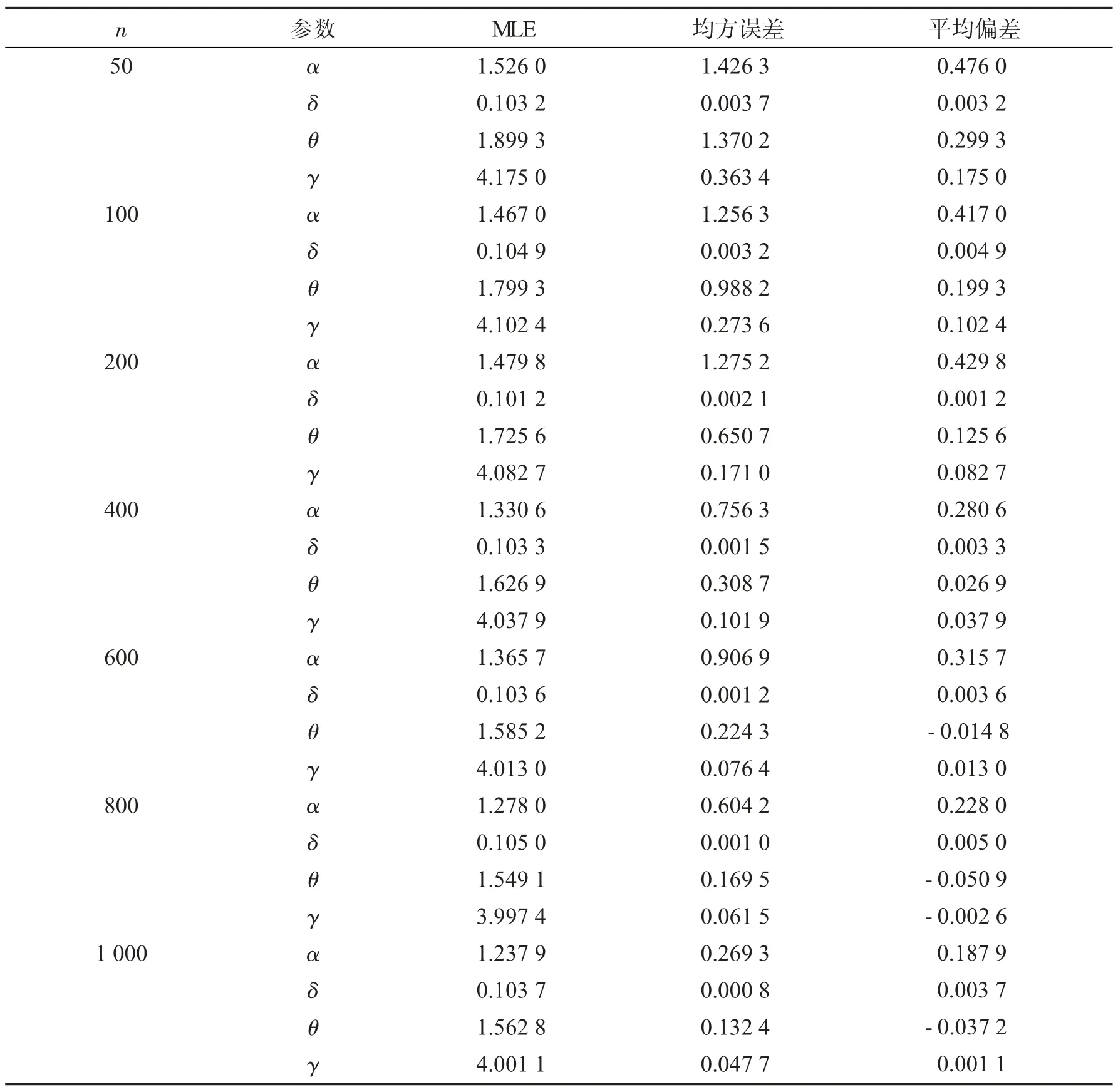
表1 数据集在不同分布情况下的参数估计和标准误差Tab.1 Parameter estimation and standard error of data set in different distributions

由表1 可以看出,随着样本量的逐渐增大,各参数的平均值越来越接近于真实值,并趋于稳定；随着样本量的增大,平均偏差逐渐减少并趋近于0；随着样本量的增大,均方误差也逐渐接近于0,说明极大似然估计具有良好的稳定性,表明本文用极大似然估计所提出的MOAPGT-II 分布的参数有效且具有一定的实际应用价值.

3 应用

在本节中,应用一个真实的数据集来说明所提出的MOAPGT-II 分布的有效性,利用R 软件中的MAXlik 包进行验证.出于比较的目的,考虑采用以下几种分布：①指数变换的Gumbel Type-II 分布（ETGT-II）、②广义逆Weibull 分布（GIWD）、③Frechet 分布（Frechet）、④II 型耿贝尔分布（GT-II）、⑤指数Burr XII（EB-XII）分布.同时还参考了Eghwerido 等[11]基于MLE 估计的对数似然函数的不同分离方法：赤池信息量准则（AIC）、改正的赤池信息量准则（CAIC）和Hannan-Quin 信息量准则（HQIC）.其中n 为样本数量,k 代表待估计参数的数量,是取对数后的似然函数值.通常定义最优的分布是给出以上准则最小值的分布

本文选取了Sindhu 等[3]讨论的数据,使用此数据有效地证明了新提出的GLET-GTII 分布的优越性,这组数据包括3 月1 日至3 月30 日期间的欧洲国家因新冠肺炎而每日死亡人数的观测结果,该数据在https：//covid19.who.int/中报告,由30 个单位组成的数据集如下：6、18、29、28、47、55、40、150、129、184、236、237、336、219、612、434、648、706、838、1 129、1 421、118、1 393、1 540、1 941、2 175、2 278、2 824、2 803 和2 667.欧洲国家新冠肺炎数据集的描述性度量结果见表2.

表2 欧洲国家新冠肺炎数据集的描述性度量Tab.2 Descriptive degree of covid-19 pneumonia data sets for European countries

通过表2 可知, 欧洲国家在3 月1 日至3 月30 日期间平均每天因新冠肺炎死亡的人数约841 人,其中最少1 天的死亡人数是6 人,最多一天的死亡人数达到2 818 人.该数据的偏度为0.92>0,呈现左偏状态.标准差为938.69,说明这组数据的离散程度较大.图4 分别绘制了这组数据的箱线图、QQ 图以及经验分布图,其中箱线图显示了这组数据集的汇总信息,阴影部分分别展现了25%、50%和75%的分位数,此图较好地指出了这组数据中的值是如何分布的.

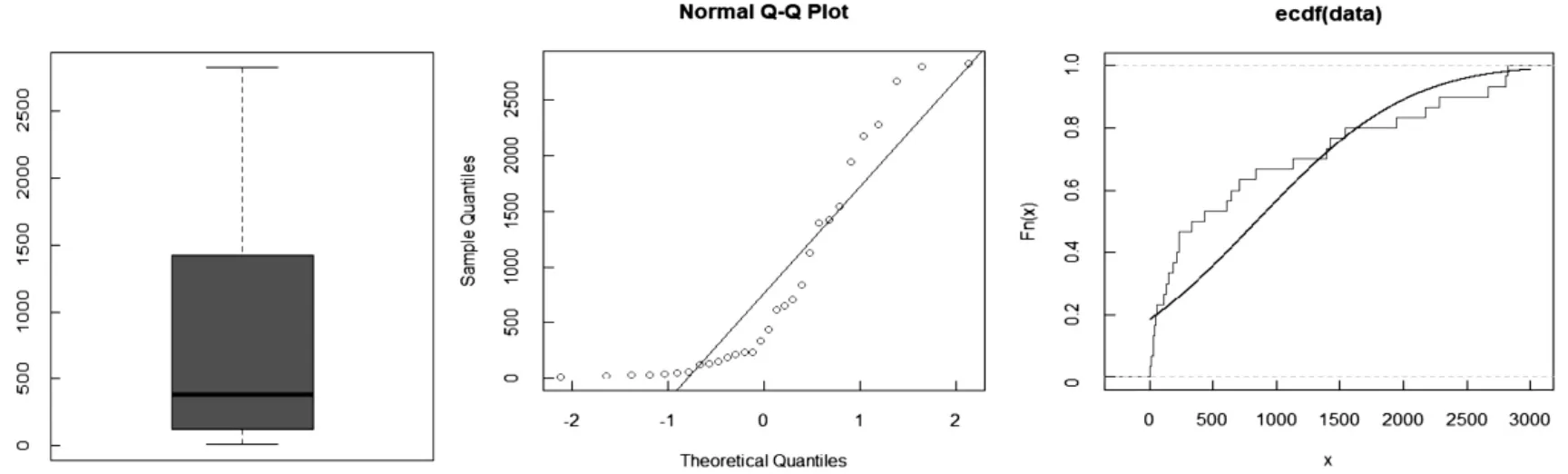
图4 欧洲国家新冠肺炎数据集的基本统计图Fig.4 Basic statistical graph of the covid-19 data set for European countries

表3 展示了这组真实数据集在六种不同的分布下进行参数估计的结果,为了检查数据是否符合MOAPGT-II分布,采用了表4 中的五种评价准则.从结果可以看出,MOAPGT-II 分布拟合当前数据与选取的五个测试分布相比,发现MOAPGT-II 分布的负对数似然值为231.90,AIC 为471.79,CAIC为472.75,HQIC 为473.58,AIC、HQIC、CAIC 和负对数似然值均小于其他分布,这表明新提出的MOAPGT-II 分布比ETGT-II、GIWD、Frechet、GT-II 以及EB-XII 分布更适合这个数据,说明这个数据与MOAPGT-II分布几乎完美匹配,MOAPGT-II 分布在所有竞争分布中提供了最佳拟合.

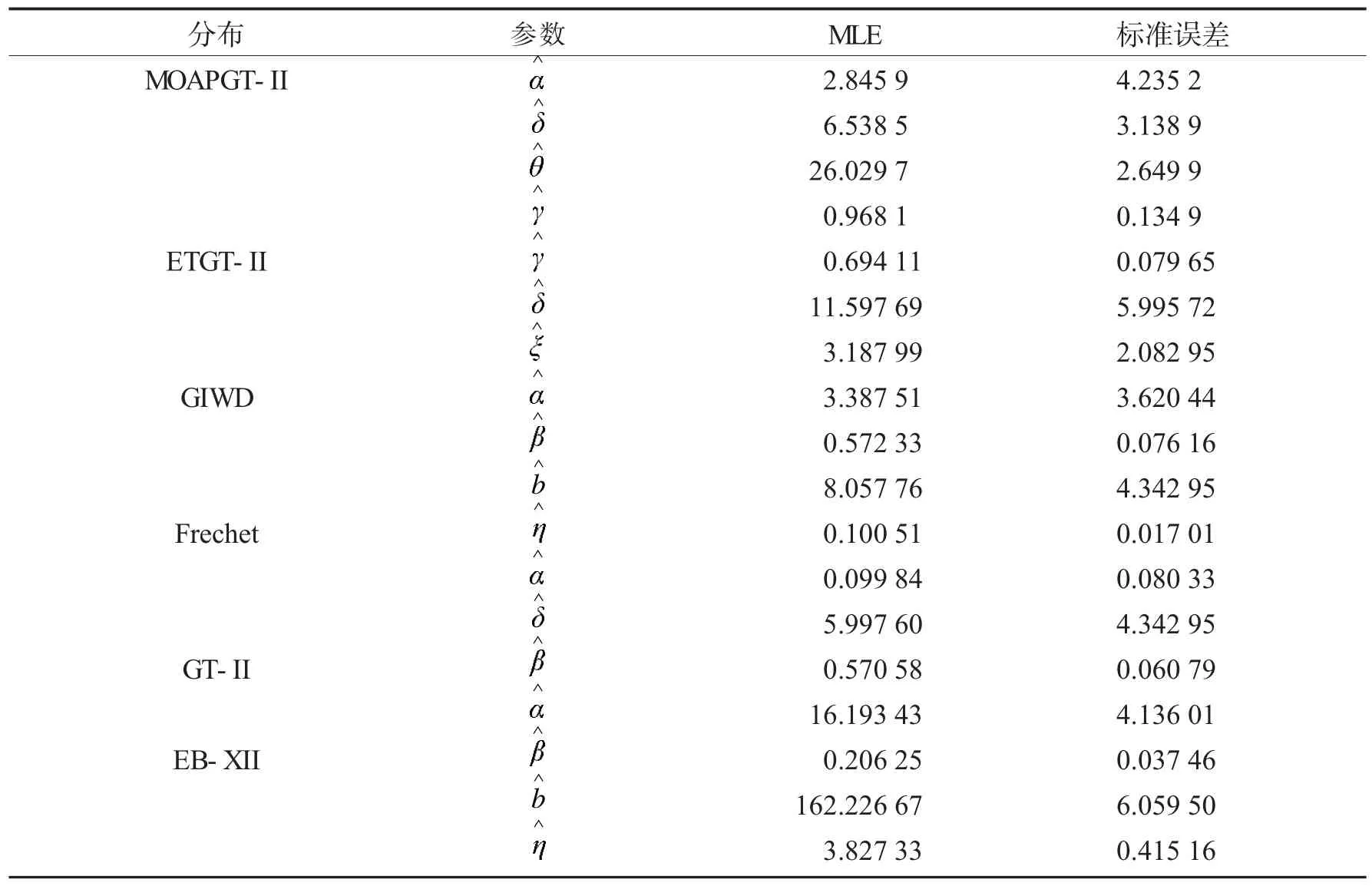
表3 欧洲国家新冠肺炎数据集在不同分布情况的参数估计和标准误差Tab.3 Parameter estimates and standard errors for different distributions of covid-19 in European national datasets

表4 对于欧洲国家新冠肺炎数据集的拟合分布评价准则值Tab.4 Evaluation criteria values for the fitted distribution of the European covid-19 data set

4 小结

本文提出了一种新的MOAPGT-II 分布及其基本性质.通过使用极大似然估计方法对该分布的参数进行估计,利用蒙特卡洛模拟分析方法得到的结果为：随着样本量的增大,其平均偏差和均方误差均会减小并接近0.最后通过一组真实的欧洲国家因新冠肺炎死亡人数的案列,将MOAPGT-II 分布与II 型耿贝尔分布、广义逆Weibull 分布、指数变换的Gumbel Type-II 分布、Frechet 分布、指数Burr XII 分布进行比较,基于经典的拟合优度指标,如AIC、CAIC 以及HQIC,发现MOAPGT-II 分布拟合该数据集的能力要优于这些分布.需要进一步研究的问题是将对数法、百分位法[12]、L 矩估计[13]、矩估计、EM算法[14-16]以及贝叶斯估计[17-18]等参数估计方法应用到本文所提出的分布上,且考虑以后可以使用boostrap 法进行区间估计.