大角度斜流下螺旋桨与导管桨尾流场特性

张 嶔, 王鑫宇, 王智程, 王天源

(中国海洋大学 工程学院,山东 青岛 266100)

螺旋桨与导管螺旋桨被广泛用作船舶、水下航行器及海洋平台动力定位系统中的主动控制装置,针对螺旋桨与导管桨尾流特性的传统研究主要基于直航设计工况下开展[1].但在船舶航运的实际工况(例如船舶紧急转向以规避碰撞等)下,螺旋桨或导管桨会由于船舶处于非常规航行姿态而经历偏航工况.在斜流工况下,由于船体、螺旋桨/导管桨和舵之间的相互作用,桨后流场形态相较于直航工况会呈现更复杂的特性,这可能会对船舶的动态响应产生较大影响.所以开展斜流情况下螺旋桨/导管桨的尾流场特性研究对于船舶、水下航行器等领域具有重大意义.

目前,开展螺旋桨与导管桨尾流特性分析主要包括试验测量及理论预报两种方法,其中理论预报主要依托于数值模拟进行.随着航运行业的发展,螺旋桨处于斜入流工况的问题逐渐受到广泛关注.物理试验方面,Felli等[2]通过试验的方法利用粒子图像测速法(Particle Image Velocimetry, PIV)技术获取直流和斜流条件下3种漂角的高分辨率尾流状态图像,基于相平均流场和瞬时流场信息,系统分析了尾流演化过程和涡旋不稳定机制,桨轴两侧尾迹不对称现象,及涡旋与螺旋桨结构的动力学影响.数值模拟分析方面, Di Mascio等[3]通过分离涡模拟(Detached-Eddy Simulation, DES)比较了螺旋桨在直流和20° 漂角斜流下尾流特征,基于相平均流场和瞬时尾流场信息分析了斜流下船用螺旋桨尾流的动力不稳定性机制,并通过动能进一步阐述了涡旋结构相互作用与失稳演化机制.Dubbioso等[4-5]基于雷诺时均方程(Reynolds-Averaged Navier-Stokes Equations, RANS)和动态重叠网格技术,对不同漂角(10°～30°)斜流下的螺旋桨进行了数值模拟,分析了单个叶片、轮毂和整个螺旋桨上的流体动力载荷(力和力矩)特征,以及局部叶片与尾流下游的压力分布特征,系统评估了小漂角斜流下螺旋桨水动力性能.国内学者Hou等[6]基于低阶势面元法建立了斜流下螺旋桨水动力性能的迭代计算模型,结果表明螺旋桨的推力和扭矩随轴向流入速度的增大而减小,随入射角的增大而增大;螺旋桨叶片表面载荷的不稳定性随轴向流入速度和入射角的增大而加剧;相比轴向流入速度,入流角对螺旋桨水动力性能不稳定性的影响更为显著.孙聪等[7]对斜流下导管桨的水动力性能及流场特性进行数值分析,结果表明,小漂角斜流工况下导管桨的推进效率会有小幅提高.周长科等[8]基于SSTk-ω模型对在0°～50° 漂角斜流下四叶导管桨的推力和扭矩进行了仿真模拟,结果发现导管的存在能够在一定范围内改善螺旋桨的水动力性能.

螺旋桨与导管桨的水动力性能研究大多在相对设计工况(直流工况)下开展,但螺旋桨与导管桨不可避免地会经常处于斜流工况下,相关研究不够深入,且大多基于小漂角斜流工况[9]对螺旋桨或导管桨推力、力矩及桨叶表面压力等展开,较少构建大漂角斜流下螺旋桨或导管桨的精细化尾流场,同时也缺乏斜流下螺旋桨和导管桨的尾流特性对比研究.为此,本文依托已有研究工作基础[10],采用结构化网格技术利用OpenFOAM基于延迟分离涡模型(Delayed Detached Eddy Simulation, DDES)结合滑移网格(Arbitrary Mesh Interface, AMI),大幅提高了大漂角斜流下螺旋桨与导管桨尾流场构建及涡旋细节捕捉的精度,对螺旋桨与导管桨在大漂角斜流(β=45°, 60°)下的尾流特性展开水动力仿真研究,对比分析二者的典型特性信息与特征差异,探究大漂角斜流下尾流与桨水动力性能的关联性,为螺旋桨与导管桨非设计工况下水动力性能研究提供理论支持与技术参考.

1 数值计算方法

1.1 湍流模型

在求解纳维-斯托克斯方程(Navier-Stokes Equations, N-S)的过程中,有雷诺时均方程、大涡模拟(Large Eddy Simulation, LES)、分离涡模拟等湍流计算模型,其中DES方法是普遍采用的既满足工程精度又节省计算资源的方法,其在边界层使用RANS方法,发挥小尺度模拟优势减少计算时间,在远场区域使用LES方法提高大尺度涡计算精度.但DES方法存在“模糊网格”的“灰色区域”过早进入LES模型以及模化应力不足的问题,DDES的出现解决了这一问题[11].

为提高计算效率,节省时间成本,在三维黏性、不可压缩的紊流模型基础上,首先进行基于多旋转参考系(Multiple Reference Frame, MRF)模型的定常数值模拟计算,以获得初始化流场信息,再依据定常流场信息基于RANS模型进行非定常数值模拟计算直至流场稳定,获得基于Spalart-Allmaras (S-A)紊流模型的非定常流场信息,最后基于DDES模型结合AMI技术提升非定常尾涡演化细节精度.

1.2 计算模型

数模研究选用导管桨和舍去导管部分的螺旋桨作为研究对象,其中导管桨模型参照Cozijn和Hallmann研究的四叶导管桨[12],由轮毂、桨叶、导管和推杆组成,螺旋桨型号为5810R,导管型号为1393.导管桨主要参数为:直径0.1 m;叶数4;螺距比1.

1.3 计算域与边界条件

以导管桨为例,计算域[10]设置为与导管桨同轴的一圆柱形区域,如图1所示.图中:U∞为入流速度;β为入流漂角;D为导管桨直径.该圆柱形计算域直径为10D,在流动方向上,向导管桨的上游延伸了2.5D,在导管桨尾迹区域延伸了10.5D.

图1 整体计算域[10]

如图1所示计算域左侧边界条件设置为速度进口边界,右侧为压力出口边界.曲面一侧为对称边界,设置为零梯度.如图2所示[13], 螺旋桨所在区域设置为旋转域,旋转域的侧面与导管桨内侧平行相距3 mm,其余部分划分为静止区域,不同的区域之间通过交界面进行数值交换.

图2 导管桨几何侧视图[13]

1.4 网格划分与工况设定

对计算模型表面及计算域采用规则和平滑的全结构化网格进行离散.对于导管桨,叶梢和导管之间设置为加密网格区域以捕捉梢涡的产生,对尾迹区域进行了适当的细化以捕捉尾迹的不稳定性流场,导管桨计算网格总数为3.3×107,螺旋桨计算网格总数为4.2×107,网格划分如图3所示,以β=45° 入流导管桨算例为例.有关网格适应性分析参考文献[10].

大角度斜流下螺旋桨与导管桨水动力数值模拟工况设定如表1所示.在恒定进速系数J=0.4的基础上,设定斜入流漂角为β=45°, 60° 以进行数值模拟计算.其中考虑斜入流漂角改变,流速固定的实际对比意义,定义实际进速系数为

(1)

式中:n为螺旋桨/导管桨转速.

依据上述工况条件进行非定常数值模拟计算,设定时间步长为1.575×10-5s,即每时间步内桨旋转0.1°,整个计算过程内桨旋转25圈,取15～25圈稳定流场数据作流场分析.

2 计算结果与分析

2.1 数值模拟计算结果验证

为确保螺旋桨和导管桨水动力特性数值模拟的准确性与可靠性,又由于导管桨相较于螺旋桨,导管结构导致的模拟过程的复杂性,故首先以导管桨为例依据表2所示的工况,在相同计算域内使β=0°,进行水动力性能的定常模拟验证,并在定常模拟得到的初始流场基础上选取进速系数J=0的工况1进行非定常流动数值模拟,详细模拟验证过程参考文献[13].与Koop等[14]的推力、扭矩数据,Cozijn等[15]的PIV试验对比结果表明,忽略推进器连接杆对尾流场的影响,基于S-A的数值模拟计算能够保证后续计算的可行性,且基于S-A紊流模型的DDES模型进行斜流工况下螺旋桨与导管桨非定常数值模拟能够在保证计算精度与可靠性的基础上,得到更高精度的流场细节.

表2 导管桨数值模拟验证工况设置[13]

2.2 相位平均尾流场特性分析

基于表1所示工况进行非定常数值模拟,得到图4所示螺旋桨与导管桨轴向推力与入流漂角变化关系曲线[10].图中:Tref取导管桨系泊工况下推力值.从图中可以看出,随着入流漂角的增大,入流速度轴向分量U∞cosβ减小,导致螺旋桨推力Tsp、导管桨螺旋桨部分推力Tp以及导管部分推力Tn、导管桨整体推力Tp+Tn均有增大趋势,且增加率也随之增大.由于导管的聚拢作用,导管桨的整体推力值与增加率均大于螺旋桨,斜流状态下,相较于螺旋桨,导管桨能提供更大的推力.

图4 不同漂角斜流下螺旋桨与导管桨推力特性曲线[10]

选定15～25圈内螺旋桨与导管桨稳定流场数据,取某一叶片旋转至0° 相位的瞬时流场数据作10圈范围内的相位平均,得到叶片在相同相位的稳定尾流场的相位平均结果,以观察尾流的周期性流动特征,并与零漂角入流工况尾流场结果对比[16].以下螺旋桨尾流相平均结果中,尾涡整体分布区域轴心l′与桨轴l之间向背流区偏转的夹角设定为α(α′),导管桨尾流相平均结果中,折角发生前尾涡整体分布区域轴心l′与桨轴l之间向背流区偏转的夹角设定为γ(γ′),折角后高速射流轴心与桨轴之间向背流区偏折的夹角设定为φ(φ′).

图5所示为螺旋桨与导管桨在β=0°, 45°, 60° 入流时的xz轴向界面的尾流流向速度场(Ux)的相位平均分布云图,并以Uref(Uref取叶尖速度)无量纲化.螺旋桨和导管桨桨叶周期性旋转产生叶梢(泄)涡,在流场中形成环状高速区,相较于零漂角入流,斜入流条件下尾流场的锯齿状特征依然存在.由于受倾斜入流的影响,螺旋桨后尾流从脱离桨盘面O处起便沿着斜流角度方向l′发展,尾涡整体分布区域轴心l′与桨轴l之间偏向角α′随入流漂角的增大而增大.但导管桨后尾流场高速区耗散段不能保持直线发展,在A(A′)处伴有小角度转折,且随着入流漂角的增加,尾流受到入流更大切向力的影响,入流漂角更大时的转折处发生位置A′较A更靠近桨盘面处,偏向角γ(γ′)、折角φ(φ′)也随入流漂角的增大而增大.

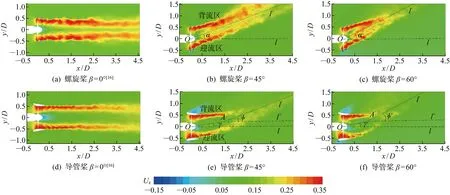
图5 β=0°, 45°, 60° 斜流下螺旋桨、导管桨相平均流向速度对比

在同一漂角斜入流下,导管桨后尾流高速区在x/D=1后逐渐耗散形成稳定的高速射流,而螺旋桨后尾流环状高速区范围更大且向桨后稳定延长,耗散幅度减弱, 表现为斜流下螺旋桨推力变化较导管桨更小.

图6 β=0°, 45°, 60° 斜流下螺旋桨、导管桨相平均压力对比

此外,螺旋桨及导管桨后尾流涡环低压区两侧有明显的差异,迎流区涡环中心压力明显大于背流区,这种不均衡性可能是由于斜流与桨后涡旋的相互干扰,加速了迎流区涡环的失稳、破碎,使中心压力升高.另外,在导管桨吸力侧盘面低压区分布同样具有沿桨轴的不对称特性,迎流侧低压范围更大,其原因可能是在迎流区导管内侧局部涡产生的影响,这将对导管桨推力均匀性产生影响.而在螺旋桨吸力侧低压不对称性主要表现在叶梢涡环中心,但这种差异并不明显.在同一漂角斜入流条件下对比螺旋桨和导管桨发现,螺旋桨涡环中心压力低于导管桨后对应涡环低压区,且螺旋桨桨毂后有清晰的低压线出现,并随流场的发展逐渐变得均匀.

图7所示为螺旋桨与导管桨在β=0°, 45°, 60° 入流时的合涡量幅值(Ω)相位平均分布云图,并以Uref/(0.5D)无量纲化.相较于零漂角工况,斜流条件下,在螺旋桨和导管桨尾流场中依然可以捕捉到叶梢(泄)涡、桨毂涡、尾缘涡等明显特征,但其失稳进程会受到斜流的影响而产生明显变化,桨轴背流侧产生明显涡旋,引起不均匀入流,成为影响流场结构与推力变化的因素.斜流下,螺旋桨背流侧梢涡不受导管影响,能够在一定范围内保持规律完整、连续分布的涡结构,迎流侧梢涡直接受到来自斜入流的干扰,自产生后便随即破裂、失稳,随着入流漂角的增大,这种梢涡消散进程更加剧烈.导管桨后迎流侧梢涡同样由于斜入流的冲刷被击碎提前发生破裂,尾涡形态变得极为不稳定,向斜流方向扩散,又由于导管对前半段尾涡的遮蔽作用,桨后尾涡形态产生明显的折角现象.

图7 β=0°, 45°, 60° 斜流下螺旋桨、导管桨相平均合涡量幅值对比

螺旋桨后尾流场整体沿偏向斜流方向的直线发展,且偏向角α(α′)随着斜流漂角的增大而增大.但导管桨尾流涡系分布与螺旋桨明显不同.图8所示为β=45°, 60° 入流下导管桨局部相平均合涡量幅值对比,以Uref/(0.5D)无量纲化.由图可见,导管背流区翼型剖面的流动攻角过大,导管外侧发生流动分离而产生局部涡脱落现象.背流区叶梢泄涡在导管内部能够保持很好的涡形状从导管后缘滑落,在与导管脱落涡接触并相互干扰后迅速破裂,导致背流侧的涡环高速低压特征不明显.随着入流漂角的增大,流动分离更剧烈,局部涡旋结构产生的区域增大,流动扰动更加剧烈,流场更加复杂.在导管桨迎流区导管部分,导管内侧的叶梢涡受到来自斜流的干扰,这可能是导致迎流区导管前缘出现高速低压特征的原因.

图8 β=45°, 60° 斜流下导管桨局部相平均合涡量幅值对比

受斜流影响,导管桨迎流区叶梢泄涡、脱落涡从导管后缘滑落后迅速破裂,消散得更快,夹角γ(γ′)、折角φ(φ′)也会随着入流漂角增大而增大,且尾流转折更早发生,转折点A(A′)呈现向桨O点处移动的趋势.无论是螺旋桨还是导管桨流场的叶梢(泄)涡、桨毂涡和尾缘涡,都会随着斜流漂角的增大,加快涡结构变形和尾流区涡结构破裂失稳演化进程.

斜流状态下,单个桨叶在旋转过程中受到的非定常载荷会随之产生非定常流,且非定常流与桨叶所处相位有关,各个桨叶的尾涡相互诱导,并受斜入流干扰,导致迎流侧、背流侧尾涡特征差异性的出现.在同一漂角斜流条件下,导管桨尾流涡结构在斜流主流效应产生的切向分量作用下,发生折角现象,且导管似乎会进一步对桨毂涡产生干扰作用,因为喷嘴会产生离心力使螺旋桨尾流集中于导管内壁面附近,也使得桨毂涡进一步失稳破碎.而螺旋桨尾涡整体分布沿直线发展,这主要是由于导管对桨后尾流起一定的遮蔽作用,可以降低尾流在初始阶段受到斜流的影响,在一定程度上保持初始射流继续沿桨轴方向发展.

图9 β=0°, 45°, 60° 斜流下螺旋桨、导管桨相平均动能对比

图10 β=0°, 45°, 60° 斜流下螺旋桨、导管桨相平均湍流动能对比

导管桨导管会将部分叶梢涡的动能转化为桨的推力,剩余能量以叶梢泄涡的形式流出,减少了梢涡湍流向桨后的发展,因此在相同漂角入流下,导管桨桨后尾流场整体湍流动能低于螺旋桨.但由于导管桨导管脱落涡的存在,使得导管桨桨后尾流场整体湍流动能形式比螺旋桨更加复杂.

2.3 瞬时尾流场特性分析

为了捕捉更清晰的流场涡旋结构细节,图11取β=45°,60° 入流下螺旋桨与导管桨最后时刻的xz轴向界面的尾流场瞬时三维涡量等值面图,并使用以Uref无量纲化的瞬时合速度幅值(U)染色.由图可以清晰地观察到斜流条件下螺旋桨迎流、背流区梢涡差异.背流区梢涡平稳发展,并逐渐经历失稳而后破碎消失于小尺度紊流中,迎流区梢涡受斜入流干扰影响较大,不会稳定地发展出螺旋涡状结构,在脱离螺旋桨盘面后迅速进入失稳破碎过程,并且随着斜流漂角的增大,梢涡进入失稳进程加快,破碎也更加剧烈.而在导管桨涡量图中,能够清晰完整地观测到背流区导管脱落涡的形成与发展,斜流下导管桨后叶梢泄涡受到来自导管脱落涡的干扰,叶梢泄涡不会呈螺旋状稳定发展,在脱离导管后迅速进入失稳进程与斜流主流混合.随着斜流漂角的增大,导管桨尾流中导管流动分离更剧烈,涡旋失稳进程加快,出现明显二次涡结构,流场变得更加复杂.

图11 β=45°, 60° 斜流下螺旋桨、导管桨瞬时涡量场的三维等值面图

螺旋桨和导管桨在相同漂角斜流下,螺旋桨由于不受导管的干扰,尾流的倾斜方向与角度完全由斜流主导,尾流涡场包含更多的涡旋结构,涡旋失稳过程更加完整,涡旋结构之间相互干扰更加剧烈,叶梢涡与斜流流场之间形成更大的速度梯度,表现出更高的流场能量(见图9),并逐渐向周围流场扩散.导管桨由于其推力大于螺旋桨,且桨后尾流在导管的遮蔽作用下,靠近桨的尾流依旧保持与导管大致对齐的方向,但在向下游的演变过程中斜流开始占据主导,这是折射角出现的原因.且叶梢泄涡更快破碎,泄涡速度高梯度区也更加集中.这些与相平均云图中得到的螺旋桨及导管桨的尾流特性分析与流体动力学结论是相一致的.

3 结论

建立了基于混合模型延迟分离涡模拟DDES,结合滑移网格AMI的非定常尾涡演化数值模型,对典型进速系数(J=0.4)大漂角(β=45°,60°)斜流下螺旋桨与导管桨的尾流场特性进行了数值模拟分析,得出的结论如下:

(1) 在典型的进速系数(J=0.4)与斜流工况下,螺旋桨和导管桨后尾流场受到斜流主流效应切向分量的影响整体呈现偏斜状态,随着入流漂角的增加,偏向角也随之增大.但导管桨后尾涡整体分布区域出现非线型的折角现象,随着入流漂角的增加,折角角度增大,折角点向桨方向靠拢.这是因为导管桨导管对斜流的屏蔽影响,可以维持初始流场在一定距离上的发展,论证了斜流下导管桨相比螺旋桨更具操纵优越性.

(2) 斜流状态下,桨叶在旋转过程中会受到周期性变化的非定常载荷,导致迎流区和背流区不均匀流场特性出现,以及在斜流主流效应切向分量的影响下,梢(泄)涡、毂涡、片涡发生相互掺混、相互负载,螺旋桨和导管桨后尾涡相互影响,流场特性比零漂角入流条件下更加复杂.导管桨背流侧导管前缘发生流动分离,迎流侧导管后缘发生梢涡融合,入流漂角越大这种现象越剧烈,导管脱落涡和桨后尾涡系产生复杂干扰,导管桨后二次涡演化明显;螺旋桨由于不存在导管,尾流场直接受到斜流影响,尾涡系不均匀性和复杂性更加剧烈.

(3) 在能量角度上,斜流剪切作用随着斜流漂角的增大得到加强,加快了导管桨和螺旋桨后尾涡结构的演化和能量的扩散.导管桨由于导管的存在,部分叶梢涡的动能转换为导管的推力,剩余能量以叶梢泄涡的形式流出,在相同的进速度系数和入流漂角条件下,导管桨尾流能量略低于螺旋桨,湍流程度也相对较低,但由于导管脱落涡的存在,尾涡系失稳掺混,使得导管桨尾涡系湍流动能形式较为复杂.