适用于中低压MMC的改进NLC调制与电容电压控制策略

张 伟, 韩俊飞, 钟 鸣, 王宇强

(1. 浙江大学 工程师学院,杭州 310027; 2. 内蒙古电力科学研究院,呼和浩特 010020;3. 内蒙古自治区电力系统智能化电网仿真企业重点实验室,呼和浩特 010020)

近年来,模块化多电平换流器(Modular Multilevel Converter, MMC)拓扑在柔性高压直流输电、交流电网异步互联等高压大容量领域获得广泛应用[1-5].而在城市直流配电网、交直流微电网、分布式能源接入、机车牵引、船舶电力系统等中低压领域,MMC同样以其输出特性好、开关频率低、结构模块化、易于扩展和实现冗余配置等优点具有良好的应用前景[6-8].不同于直流输电等高压领域,中低压MMC桥臂子模块数量通常较少,在传统调制和控制策略下输出电平数低,电能质量相对较差,难以满足高品质用电负荷要求.因此,如何以较少数量子模块实现高输出电平数以降低谐波含量,是中低压MMC需要解决的一个重要问题[9-10].

目前,MMC调制技术主要包括载波移相脉宽调制(Carrier Phase Shift Pulse Width Modulation, CPS-PWM)[11-12]等多重载波调制和最近电平逼近调制(Nearest Level Control, NLC)[13-14]两大类.CPS-PWM调制技术广泛应用于级联H桥型变流器,输出特性好但开关频率相对较高,且需为子模块配置额外的闭环均压控制,在运行环境复杂的直流配电系统中不利于提高系统可靠性.NLC调制策略无需三角载波,简便可靠,开关频率低;但其输出电压阶梯波电平数受限于桥臂子模块数量.为提高中低压MMC输出电压质量,文献[14]中在CPS-PWM方法基础上提出一种增加电平数的改进调制方法,通过设置上、下桥臂三角载波相位差获得更高的输出电平数.文献[15]中将这种思路拓展应用于NLC调制,采用设置取整函数偏置等方式,调整MMC桥臂输出电压阶梯波阶跃时刻,实现2N+1电平输出(N为MMC桥臂子模块数).文献[16]中在上述方法基础上,进一步引入无差拍控制器,调整取子模块投入数降低了输出电压总谐波含量(Total Harmonic Distortion, THD).

上述调制策略均能改善低电平MMC的输出特性,但设置上、下桥臂阶梯波相位差获得更高输出电平数的同时,也使得给定交流电压与交流参考电压间出现一定误差,导致在原有相间环流中引入新的非特征次谐波电流.基于类似思路,文献[17]中结合NLC调制策略和环流抑制,以桥臂电流谐波反馈作为上、下桥臂导通模块差模分量的修正量,既能提高输出电平数,还减少桥臂输出电压阶梯波相位差带来的非特征次谐波电流.

此外,为保证系统可靠性,直流配电系统和直流微电网通常采用下垂控制等方法实现电压稳定与潮流分配[18-20].然而,传统NLC调制策略下的MMC依靠恒定数子模块级联建立直流母线电压,变流器运行功率、直流母线电压等外部电气特性与子模块电容储能相互耦合;当系统运行工况或发生故障时,直流母线电压在下垂控制策略下偏离稳态运行点,子模块电容电压平均值也将随之偏离额定值.该偏差值与MMC电容电压交流波动量叠加,将显著增加电容过压风险,严重时可能导致换流阀过压闭锁.因此,配电系统中MMC需采用耐压等级更高的直流电容和功率器件,不利于减小设备体积和提升功率密度.文献[21-22]中针对全桥型子模块和半桥型子模块构成的混合型MMC,提出一种电容参数优化设计方法,能够实现电容电压波动抑制进而降低子模块电容选值标准.文献[23]中在混合型MMC的半桥型子模块调制电压中注入3次谐波分量,同时在桥臂环流中注入二倍频分量,进一步减小电容电压波动幅值.此外,改进子模块拓扑结构、采用可调桥臂电抗器等方式也能一定程度降低电容电压波动幅值[24-26].上述研究主要从MMC内部电气特性调控入手,忽视了换流站外部电气量和直流输配电系统协调控制模式的影响.

针对中低压MMC子模块数较少、直流母线电压易受扰动的实际问题,提出一种阶梯波调制与电容电压控制相结合的MMC改进控制策略.该方法简便易用,一方面能够增加输出电平数,降低输出电压THD;另一方面实现了MMC电容电压与直流母线电压的解耦控制,降低子模块欠压和过压风险.最后,在MATLAB/Simulink仿真模型和RTDS硬件在环测试中对本文所提出的控制策略进行验证.

1 中低压MMC数学模型

应用于城市直流配电网、交直流微电网、分布式电源接入等典型场景的中低压MMC具有与高压领域类似的拓扑结构.图1所示为典型的三相六桥臂MMC拓扑.每个桥臂含有N个子模块(Sub-Module,SM)和1个桥臂电感Larm.图中:P、N、o分别为直流母线正、负极端子、假想的电位参考点;ua,up与ua,low分别为A相上、下桥臂电压;ia,up和ia,low分别为A相上、下桥臂电流;ia、ib、ic分别为A、B、C相交流电流;IDC、uDC分别为直流母线电流、电压.子模块可以采用半桥型、全桥型等拓扑结构,本文以应用最广泛的半桥型MMC为例进行分析.

图1 MMC电路拓扑

根据基尔霍夫电压定律并忽略桥臂电阻,以A相为例,得到MMC桥臂电压方程:

(1)

式中:uao为A相交流输出电压;t为时间.

根据基尔霍夫电流定律,得到桥臂电流方程:

(2)

式中:icir为桥臂环流谐波分量.根据式(1)～(2),分别得到MMC交流侧和直流侧基本模型,即

(3)

不妨设MMC A相交流输出电压为

(4)

式中:m为调制比;ω为角频率.根据传统NLC调制策略原理,上、下桥臂在任一控制周期导通子模块数计算方法为

(5)

式中:UC, ave为子模块电容电压平均值;round()表示最近取整函数.

根据MMC数学模型可知,传统NLC调制方式应用于中低压MMC存在两个问题:①当子模块数量较少时,MMC输出电压平数少,谐波含量较高;②MMC直流侧串联子模块数恒定,电容电压与直流母线电压耦合,进而受直流系统运行工况和控制特性的影响.

2 中低压MMC的NLC调制策略

2.1 输出电平解析

传统NLC调制策略的基本原理是利用阶梯波逼近正弦调制参考波.在离散控制系统中,MMC在相邻两个阶梯内上、下桥臂导通模块数增量为正整数,即桥臂电压必须是以电容电压UC,ave为阶跃幅值的阶梯波.

(6)

式中:uup和ulow分别为上、下桥臂电压;Δnup和Δnlow分别为上、下桥臂导通模块数在相邻阶梯内的增量;i和i+1代表相邻两个控制周期的子模块投切时刻.传统NLC调制下,MMC直流侧导通模块数恒定为N,即

(7)

式中:ncom为上、下桥臂导通模块数共模分量.

由于直流侧导通模块数恒定,所以上、下桥臂导通模块数增量互补,即

Δnup=-Δnlow=Δnref

(8)

式中:Δnref为参考电压变化导致的桥臂导通子模块数增量,Δnref∈{-N,N}.

MMC交流输出电压可表示为

(9)

式中:ndiff为上、下桥臂导通模块数差模分量.

相邻两个阶梯内,MMC交流电压增量为

Δuac=uac(i+1)-uac(i)=ΔnrefUC,ave

(10)

由式(10)可得:传统NLC调制下,MMC交流输出电压是以电容电压UC,ave为阶跃幅值的阶梯波,换流器最大输出电平数为N+1.以每桥臂4个子模块MMC为例,NLC调制策略下交流输出电平数nac和对应的桥臂导通模块数如表1所示.

表1 子模块开关能量组合状态

2.2 改进NLC调制方法

在高压直流输电等高电压等级场合下,MMC桥臂子模块数量很高,NLC调制阶梯波近似于理想正弦波.但在中低压应用领域,传统NLC方法输出电平数较低,谐波含量大的问题凸显.为提升输出电平数,提出一种简单实用的改进型NLC调制方法.即在上、下桥臂导通模块数计算式中,引入阶梯波修正量,即

(11)

式中:直流分量nDC=N/2;交流分量nac=(nlow-nup)/2;nM为修正量.相邻两个阶梯内上、下桥臂电压增量为

(12)

式中:ΔnM=ΔnM(i+1)-ΔnM(i).

因此,MMC交流电压在相邻阶梯的增量为

(13)

由式(13)可得:当相邻阶梯内修正量增量ΔnM为奇数时,MMC输出电压阶跃幅值为0.5倍电容电压;当ΔnM为偶数时,MMC输出电压阶跃幅值为整数倍电容电压.根据交流参考电压不断改变nM值奇偶性,即可实现桥臂级联子模块数不变条件下将最大电平数扩展为2N+1.根据上述两种情况,当2ndiff为偶数时,修正量取值nM=0.当2ndiff为奇数时,修正量nM取值1或-1.根据上述分析,改进的NLC控制框图如图2所示.

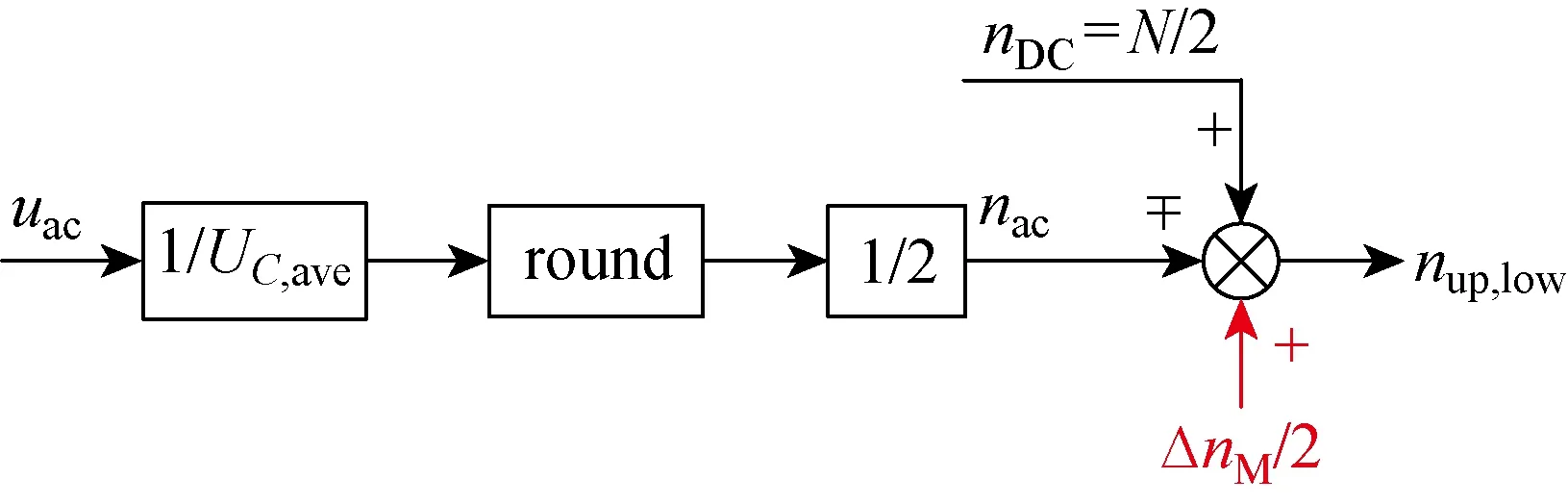
图2 改进NLC调制策略

以桥臂子模块数为4的MMC为例,当修正量nM取值为{0,1}时,ΔnM为奇数,MMC输出电平如表2所示.引入桥臂导通模块数修正量nM,可以相应改变导通模块数差模分量的奇偶性,从而进一步提升换流器交流侧输出电平.

表2 改进NLC输出电平

3 基于改进NLC调制电容电压稳定控制

3.1 电容电压解耦控制

基于上述改进NLC调制策略,MMC能够在子模块较少条件下获得更高的输出电平数,从而提高交流电能质量.但相应地,由于桥臂阶梯波修正量nM的引入,MMC直流侧串联子模块数不再恒定为N,所以MMC直流侧数学模型修正为

(14)

nM奇偶性发生变化时,MMC直流侧被直流母线电压箝位的子模块电容数量也相应改变.这导致三相间环流变化[11],同时也引起子模块电容电压平均值偏离额定值.

(15)

由于中低压MMC子模块数较少,所以设置修正量nM的取值为{-1, 0, 1},其中±1与0交替插值,从而实现2N+1电平扩展.

如图3所示,在直流母线电压稳定于额定值条件下,若MMC修正量nM=0,则表现为传统NLC调制,满足电容电压UC,ave等于额定值UCN;若修正量nM∈{0, 1},则直流侧串联模块数超过N,电容电压低于额定值,UC,aveUCN.

图3 子模块电容电压与nM的关系

针对上述问题,对所提出的改进NLC策略中修正量nM进行改进,以实现电容电压稳定.在直流母线电压稳定于额定值时,设置nM为幅值±1、占空比σ为0.5的方波,如图3(b)所示,即可实现电容电压平均值UC,ave=UCN.但在实际直流配电系统或直流微电网中,多个换流站通常采用下垂控制或电压裕度控制等多点协调控制策略[13-14]以提高系统可靠性.此类控制策略下,系统运行工况变化时往往导致直流母线电压偏离稳态运行点,进而导致MMC电容电压发生偏移.

结合图3中修正量nM与系统协调控制对电容电压的影响,在改进NLC调制策略基础上,提出一种中低压MMC电容电压稳定控制方法.引入电容电压平均值反馈控制,对桥臂阶梯波修正量nM的方波占空比σ进行实时调节.首先计算子模块电容电压偏差值ΔUC,ave,利用比例-积分(PI)控制器调节方波占空比参考值σ:当直流母线电压偏高导致偏差值ΔUC,ave>0时,占空比σ增大,从而降低电容电压;当偏差值ΔUC,ave<0时,占空比σ减小,使得电容电压升高.具体方法如图4所示.

图4 基于改进NLC调制的电容电压控制

3.2 控制特性分析

为分析上述控制策略对MMC电容电压的影响,分别计算NLC调制下电容电压的直流分量、基频分量和二倍频分量幅值.在稳态运行条件下,假设子模块电压均衡良好且元器件参数一致,根据文献[20]可得电容电压解析式:

(16)

(17)

(18)

式中:φa为A相相角;C为子模块电容值.

传统NLC调制方式下,直流母线电压偏移导致的MMC电容电压交直流分量幅值变化分别为

(19)

改进NLC策略下,考虑修正量nM改变MMC直流侧串联子模块数,则电容电压直流分量稳定于额定值,基频分量和二倍频分量幅值计算如下:

(20)

对比传统调制策略,基于改进NLC调制的电容电压反馈控制下,MMC子模块电容电压波动中的基频和二倍频分量与修正量nM正相关,即当直流母线电压升高时,修正量nM为正,则电容电压直流分量减小,但纹波系数增大;当直流母线电压降低时,修正量nM为负,电容电压直流分量升高,纹波系数减小.由于式(20)中右侧含高阶小量,所以纹波系数变化率远低于直流分量.综合考虑电容电压交直流分量,所提出的稳定控制能够有效抑制不同运行工况下的MMC电容电压波动范围.

4 仿真验证

为验证所提中低压MMC改进NLC调制策略和电容电压稳定控制方法的有效性,在MATLAB/Simulink仿真软件中搭建MMC电磁暂态仿真模型.简单起见,中压直流(MVDC)系统直流侧母线电压由受控电压源模拟,交流侧连接阻性负载.MMC分别采用传统NLC调制策略、载波层叠脉宽调制(Carrier Level-Shifted Pulse Width Modulation, CLS-PWM)[27]方式及本文改进NLC调制方法,以进行对比验证.详细仿真参数设置为:额定直流电压±350 V;交流额定电压380 V;每桥臂子模块数4个;子模块额定电容电压187.5 V;桥臂电感10 mH;模块电容2 mF;采样频率20 kHz.

MMC稳定运行于额定工况下,交流侧连接阻性负载(5 Ω).分别采用传统NLC调制方法、CLS-PWM调制方式及本文提出的改进NLC调制策略,对比3种调制方式下的MMC运行特性和输出电能质量.其中改进NLC调制方法中修正量nM为幅值±1、占空比0.5的方波.仿真结果如图5～7所示.

图5 传统NLC策略仿真波形

以A相上桥臂为例,传统NLC调制策略的MMC交流相电压输出电平为5(调制比为0.89),如图5所示.图中:uC为子模块电容电压.其上、下桥臂参考导通模块数在同一时刻动作,交流侧输出电压阶梯波阶跃值为电容电压的整数倍.由于输出电平数较低,MMC交流电压(uabc)和交流电流(iabc)在阻性负载下出现明显畸变.在额定工况下,交流电流幅值约为50 A,电流THD为5.66%.电容电压在额定值附近周期性波动,稳态下波动幅值约为18 V,纹波系数为9.6%,在实际直流配电系统中MMC子模块电容电压波动低于±10%即为可以接受.对电力系统等中低压领域而言,传统NLC调制方式下MMC输出电压和输出电流谐波含量较高,难以满足部分对电能质量有较高要求的用电负荷需要.

CLS-PWM调制方式的MMC交流相电压输出电平仍为5,如图6所示.该调制策略下,MMC交流电压和交流电流在阻性负载下的畸变率明显优于传统NLC调制方式,交流输出电流THD约为2.13%.这是因为其上、下桥臂参考导通模块数在传统NLC阶梯波最高/低阶梯处投切.此时,MMC运行于稳态工况时的电容电压波动于168～205 V,纹波系数约为10%.因此,该调制方式下能够满足部分对电能质量有较高要求的用电负荷需要,但其需为每个子模块配置额外的闭环均压控制,在运行环境复杂的直流配电系统中不利于提高系统可靠性.

图6 CLS-PWM策略仿真波形

改进NLC调制方式的仿真结果如图7所示.由于调制比限制,MMC交流相电压输出电平数为7.在额定工况稳定运行时,直流侧串联模块数修正量nM平均值为0.MMC上、下桥臂导通模块数在传统NLC阶梯波上投切.该调制策略下,MMC交流交流输出电压电平数增加为7,交流输出电流THD约为2.65%,电流畸变率明显优于传统NLC调制方式.改进NLC调制方式下,MMC运行于稳态工况时的电容电压波动为169～205 V,纹波系数约为10%.

图7 改进NLC策略仿真波形

稳态仿真结果显示,所提出的改进NLC调制策略能够有效提升MMC输出电平数并改善交流输出电能质量.相同运行条件下,交流电流THD由传统NLC的5.66%下降至2.65%,接近CLS-PWM的2.13%.另一方面,由于修正量nM的引入,桥臂电压参考值包含{-1, 0, 1}的高频分量.该分量一方面使得MMC输出电平数扩展至2N+1,但也在直流电压和相间环流中引入非特征次谐波分量.

为进一步验证中低压MMC电容电压稳定控制方法,对直流母线电压阶跃运行条件进行仿真分析,如图8和图9所示.仿真初始时刻至1.0 s,MMC稳定运行于额定直流母线电压750 V;1.5 s时直流母线电压升高至830 V,约1.1 (p.u.);1.0 s后直流母线电压跌落至670 V,约0.9 (p.u.).对比传统NLC调制和改进NLC调制方法的电容电压,结果如下.

图8 直流母线电压波动时传统NLC电容电压

图9 直流母线电压波动时改进NLC电容电压

图8为传统NLC调制方法仿真结果.仿真初始阶段0～1.0 s,直流母线电压为额定值750 V,电容电压稳定于额定值187 V附近,波动范围为168～205 V;1.0～1.5 s,直流母线电压升高后,电容电压波动范围约为194～230 V;1.5～2.0 s,直流母线电压跌落,子模块电容电压亦随之减小,波动范围约为142～176 V.在整个仿真过程中,MMC子模块电容电压随直流母线电压在0.76～1.23 (p.u.)范围内大幅变化,已接近甚至超过子模块过压和欠压保护阈值.当直流母线电压变化时,MMC电容电压纹波系数基本不变;可见,由于下垂控制导致的电容电压直流分量偏移,已经超过电容电压基频和二倍频波动最大幅值(额定功率),成为影响器件参数选型和安全裕度的主导因素.

图9为电压稳定控制仿真结果.得益于直流侧引入导通模块数修正量实时调整,MMC换流阀内部储能与外部传输功率相解耦.当直流母线电压升高后,电容电压平均值的直流偏移量约为0.7%, 但电容电压波动幅值增大至156～208 V,纹波系数约为14%.相比传统NLC调制方法,改进方法的最大电容电压由约230 V降低至208 V.当直流母线电压跌落后,MMC子模块电容电压平均值约为193 V,波动范围限制于180～206 V,纹波系数减小至约7%,低于传统方法的9%,与式(20)的理论分析相吻合.

综合上述仿真结果,本文提出的改进NLC调制及电容电压稳定控制方法,在提升MMC输出电平的同时,能够在直流母线电压波动条件下维持电容电压基本稳定,有效抑制电容电压偏移;有利于降低电容和开关器件的耐压选型标准,提高设备可靠性.

5 RTDS硬件在环测试

为进一步验证改进NLC调制及其电容电压稳定控制策略,在基于RTDS的6.4 kV/4.5 MW MMC平台中进行硬件在环测试(Hardware in the Loop, HIL),如图10所示.测试工况与仿真类似,MMC直流母线电压由受控电压源模拟,交流侧连接阻感负载.MMC分别采用传统NLC调制策略和本文改进NLC调制方法进行对比验证.详细仿真参数设置为:额定直流电压±3.2 V;交流额定电压3.1 V;每桥臂子模块数4个;子模块额定电容电压1.6 V;桥臂电感13 mH;模块电容12 mF;采样频率20 kHz.

图10 硬件在环测试平台

5.1 稳态运行

MMC稳定运行于额定工况下,交流侧连接阻感负载.分别采用传统NLC调制和本文提出的改进NLC调制策略,对比两种调制方式下的MMC运行特性和输出电能质量.RTDS测试结果如图11～12所示.

图11 传统NLC策略测试波形

传统NLC调制策略下HIL测试结果如图11所示.图中:uup,low为A相上、下桥臂电压.以A相为例,由于输出电平数较低,MMC交流电压中存在较为明显的畸变,经傅里叶分解得到THD约为3.39%.交流电流幅值约为1.0 kA,电流THD为1.76%.该调制方式下桥臂电压中直流分量稳定于3.2 kV,电容电压在额定值附近周期性波动,纹波系数约为3.2%.

改进NLC调制方式的HIL测试结果如图12所示.相比于传统NLC调制策略,MMC交流电压参考波电平数由5增加为9,因此其交流电压THD约为2.25%,交流电流THD约为1.15%,分别降低约33.6% 和34.7%.改进策略的交流电能质量明显优于传统NLC方法.MMC在稳态工况下的电容电压稳定于额定值1.6 kV附近波动.相比于传统方法,由于在桥臂导通模块数直流分量中引入修正量,导致电容电压直流分量出现小幅波动,两者纹波系数没有显著区别.

稳态条件下的HIL测试结果如图13所示.图中:U0为基频分量的幅值;Mag为各倍频分量幅值相较于基频分量幅值的比例;基频频率f0=50 Hz.所提出的改进NLC调制策略能够有效提升电平数较低的MMC交流输出电能质量.相同运行条件下,交流电流THD相比传统NLC的1.76%下降至1.15%.

5.2 变工况运行

为了验证中低压MMC电容电压稳定控制策略的有效性,对直流母线电压阶跃运行条件进行试验.测试条件如下,MMC直流母线电压初始时刻稳定于额定值6.4 kV;1.5 s时直流母线电压升高至7.1 kV,约1.1 (p.u.);2.5 s后直流母线电压恢复额定值,3.0 s跌落至5.7 kV,约0.9 (p.u.).分别对传统NLC调制方法和改进NLC方法在相同运行条件下进行对比仿真测试.

图14为传统NLC调制方法测试结果.当直流母线电压为额定值6.4 kV时,电容电压直流分量约为1.6 kV;当直流母线电压升高至1.1 (p.u.)时,电容电压直流分量随之大幅偏离额定值并剧烈振荡.3.0 s后直流母线电压跌落,子模块电容电压亦随之减小,并最终稳定于约1.4 kV.整个实验过程中,电容电压波动范围约为1.2～2.0 kV,已接近甚至超过子模块过压和欠压保护阈值.

图15为改进控制方法测试结果.图中:uDC为直流母线电压.整个实验过程中,MMC电容电压未发生显著偏移.当直流母线电压升高时,电容电压波动幅值略微增大;当直流母线电压降低时,纹波系数略微减小.MMC电容电压波动范围限制于1.52～1.68 kV,有利于提高换流阀和子模块电压安全裕度,尤其是两端或多端的直流系统.值得注意的是,改进NLC调制方法下,由于在MMC直流侧引入幅值为1个电容电压的高频分量,对环流抑制等有一定影响,所以在实际直流配电系统中可采用改进环流抑制算法或配置高频滤波器等方式加以改善.因此本文所提改进NLC策略几乎不会给直流系统的稳定性带来不利影响.

图15 改进NLC策略电压波形

6 结语

针对应用于城市直流配电网等中低压领域的MMC输出电平少、电能质量较差的问题,提出一种改进NLC调制策略,能够实现2N+1电平输出,简单实用.在此基础上,引入电容电压反馈,提出一种中低压MMC子模块电压稳定控制方法,实现子模块电容电压与直流母线电压的解耦控制.基于RTDS的HIL测试结果显示,4模块MMC采用改进NLC调制策略时,交流电压和交流电流THD分别从3.39%和1.76%降低至2.25%和1.15%.当直流母线电压偏离额定值时,所提电容电压控制方法能够稳定控制子模块电压于额定值附近,电压波动范围由1.2～2.0 kV降低至1.52～1.68 kV,避免电容过压或欠压风险,有利于降低器件选型难度和提升设备安全裕度.但缺点是在MMC直流侧引入高频噪声不利于环流抑制.