考虑维修效果差异性的顺序预防性维修策略

黎新龙, 冉 琰, 张根保,2,3, 何 彦,2

(1. 重庆大学 机械与运载工程学院, 重庆 400044; 2. 重庆大学 机械传动国家重点实验室, 重庆 400044; 3. 重庆文理学院 智能制造工程学院, 重庆 402160)

预防性维修在一定程度上能够降低设备发生故障的概率,减少停机损失,在工程中被广泛应用[1-2].通常,预防性维修可以分为基于时间的预防性维修和基于状态的预防性维修.随着传感技术的发展,基于状态的预防性维修受到了广泛关注.但状态维修较高的成本投入和相关技术要求[3],对一些不便于状态监测和维修预算较少的重要设备,基于时间的预防性维修依然是当前维修策略中不可或缺的一种重要手段.基于时间的预防性维修可进一步分为等周期预防性维修和非等周期预防性维修(顺序维修).相比等周期预防性维修,顺序预防性维修更能节省维修成本[4].因此,不少学者对顺序预防性维修展开了研究.Nakagawa[4]最早提出了顺序预防性维修,指出顺序预防性维修比定期预防性维修更具实用性;Zhu等[5]针对系统在不确定非周期变化应力下的设计和维修问题,提出了一种集系统设计和顺序预防性维修计划于一体的两阶段随机规划模型,能有效降低设备的维修成本;Zhou等[6]提出了一种顺序不完全预防性维修模型来量化城市公交车的维修效率,对城市公交维修管理决策与优化具有重要意义.顺序预防性维修策略[7-8]受到了极大的重视并取得了不错的效果,有效减少了设备维护成本,但还存在一些问题值得进一步研究.首先,上述模型通常假设预防性维修对可修设备所有类型的故障都起作用,它能够降低设备的总体故障率或者有效役龄.但实际上,由于预防性维修都是一些比较固定的操作(清洗、更换机油等),其对磨损等损伤类故障能起到较好的作用,但对疲劳断裂等本质疲劳类故障却影响甚微[9],没考虑到这点制定的维修策略可能产生不必要的维修费用.其次,在以往的维修策略中,维修决策对象通常选择的是一个部件或者系统.部件或者系统结构复杂包含的零件数过多,粒度过大,制定的维修决策不够精准,容易造成过维修而浪费维修资源.同时,也不便于故障的诊断和定位.例如,传统的故障定位到了齿轮箱,然而齿轮箱包含很多个零部件并不能明确齿轮箱发生故障的部位,还需要进行进一步的诊断与检测,花费的时间较多.张根保等[10-11]提出了元动作理论.Yu等[12-13]和Zhang等[14]将设备通过“功能-运动-动作”结构化分解方法得到元动作单元,相比部件或者系统,元动作单元拥有更少的零件和更简单的结构,便于故障诊断与定位;Yu等[15]基于元动作找出了机械系统所有的潜在故障模式,避免了故障模式和故障原因的混淆,便于故障分析;Zhang等[16]研究了基于元动作的故障诊断方法.这些难点问题的解决为研究基于元动作单元的维修奠定了基础.以元动作单元为维修决策对象制定的维修策略更加精准,一定程度上能避免过维修,充分利用设备的使用寿命.

基于以上考虑,以元动作单元为预防性维修决策对象,考虑预防性维修的不完美性及其对不同类型故障维修效果的差异,基于广义几何过程(GGP)[17-18]建立了元动作单元的顺序预防性维修模型,确定了元动作单元在给定最大预防性维修次数下的最优维修策略.最后,分析了维修成本等因数对最优维修成本率以及最优维修策略的影响.

1 模型假设

(1) 对元动作单元采用顺序预防性维修(N,x1,…,xN)和修复性维修相结合的维修策略.以x1,x2,…,xN为维修时间间隔对元动作单元进行预防性维修,在第N次预防性维修时对元动作单元进行更换,使其修复如新.当元动作单元出现故障时,对元动作单元进行修复性维修(最小维修),使其恢复到故障之前的状态.

(2) 元动作单元中存在两类故障:损伤类故障和本质疲劳类故障.预防性维修对可以降低损伤类故障的故障率,但对本质的疲劳类故障不起作用.

(4) 元动作单元初始时刻处于全新状态,故障率为0.

(5) 各类型维修操作时间相对元动作单元寿命很短,因此忽略不计.

2 元动作单元故障率描述

考虑元动作单元中存在损伤类故障和本质疲劳类故障[9],假设元动作单元总的故障率函数为

λ(t)=u(t)+v(t)

(1)

式中:t表示时间;u(t)表示元动作单元损伤类故障的故障率函数;v(t)表示元动作单元本质疲劳类故障的故障率函数.

一般情况下机电产品初始故障率服从韦布尔分布,则元动作单元总的初始故障率函数为

λ0(t)=αβtβ-1

(2)

式中:α和β分别为形状参数和尺度参数.

损伤类故障的初始故障率函数u(t)和本质疲劳故障的初始故障率函数v(t)可表示为

(3)

式中:e和f分别为元动作单元损伤类故障和本质疲劳故障的比例因子,满足e+f=1.

3 GGP及GGP预防性维修

GGP是基于几何过程(GP)的扩展,在设备运行时间建模方面更灵活,它维修能够反映预防性维修对系统维修效果的变化[17-18].同时,它能很好地描述预防性维修的不完美性以及维修效果随着预防性维修次数的增加而减弱的现象.因此,采用GGP建立元动作单元的顺序预防性维修模型.

定义1GGP

设{Zk,k≥1}为非负随机变量序列,k=1,2,3,…时,如果Zk+1/Zk=ak,则当{Zk,k≥1}满足以下条件时,其服从GGP[17-18].

(1) 随机变量之间相互独立.

(2) 对任意整数k≥1,ak>0.

(3) 当k≥1时,存在Fk(t)=F(a0,a1,…,ak-1t),a0=1,F(t)是Z1的累积分布函数,Fk(t)是Zk的累积分布函数.

当ak恒等于1时,Z1=Z2=…=Zk,{Zk,k≥1}是一个更新过程;当ak恒小于1时,Z1Z2>…>Zk,{Zk,k≥1}是一个递减GGP.

定义2GGP预防性维修

设{Zk,k≥1}表示元动作单元预防性维修的时间间隔序列,如果{Zk,k≥1}满足GGP的条件,那么,预防性维修被称为“GGP预防性维修”.考虑现实中预防性维修效果随其维修次数的增加而减弱,因此,本文“GGP预防性维修”的参数ak递增,1≤a1≤a2≤…≤ak.同时,考虑预防性维修仅对损伤类故障起作用,故本文GGP预防性维修只能调整损伤类故障的故障率.当α=0.01,β=2.5,a1=1,a2=1.2,e=0.9,f=0.1时,预防性维修前后元动作单元各故障率函数的变化如图1所示.其中,PM表示预防性维修,uk(t)表示损伤类故障在第k个预防性维修周期的故障率函数.vk(t)表示本质疲劳类故障在第k个预防性维修周期的故障率函数.由于预防性维修对本质疲劳类故障不起作用,因此vk(t)在整个时间段内都是同一个函数.λk(t)表示元动作单元在第k个预防性维修周期总的故障率函数,k=1,2.

图1 预防性维修前后元动作单元故障率的变化情况

根据Wang等[17-18]研究,可推得元动作单元损伤类故障在第k个预防性维修周期上的故障率函数uk(t)为

(4)

假设元动作单元第k个预防性维修周期为xk,那么在第k个预防性维修周期内期望故障的总次数为

(5)

4 顺序预防性维修建模

元动作单元经历N-1个周期长度分别为x1,x2,…,xN-1的不完全预防性维修,再经历xN进行第N次预防性维修时对元动作单元进行更换,使其修复如新.则在整个更新周期内,其维修成本率可以表示为

C(N,x1,…,xN)=

(6)

(7)

(8)

用式(6)对xk求偏导,并令其等于0,可得:

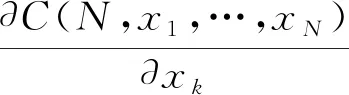
C(N,x1,x2,…,xN)

(9)

用式(6)分别对x1,x2,…,xk求偏导,并令其等于0,则可得:

(10)

由式(10)推出:

u1(x1)=u2(x2)=…=uN(xN)

(11)

令u1(x1)=u2(x2)=…=uN(xN)=D, 推出:

(12)

将式(12)代入式(10)中任意一个方程,从而可推出:

(13)

(14)

利用搜索方法,可以找出元动作单元的最优维修策略(N*,x1, …,xN*),求解算法流程如图2所示.

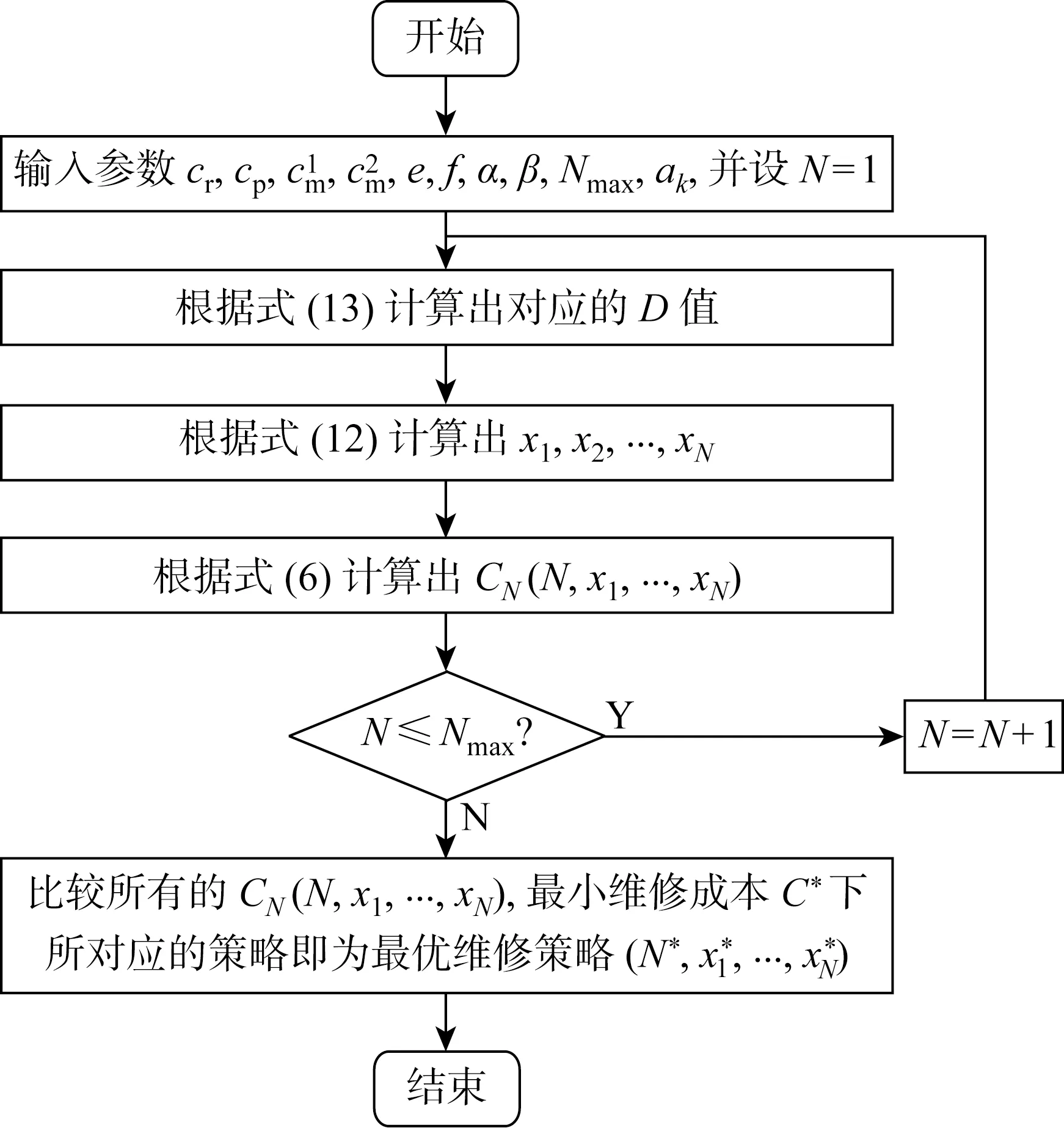
图2 求解算法流程图

5 算例分析

预防性维修效果主要体现在比率ak上.ak越大,预防性维修效果越差,反之维修效果越好.Wang等[17]考虑实际中预防性维修效果随着维修次数的增加呈现减弱的趋势,预防性维修效果参数ak的取值为

ak=eνk

(15)

式中:k=0,1,2,…,N;ak>1表示预防性维修效果随着预防性维修次数的增多而减弱;ν为调整因子,ν>0,ν越大预防性维修效果相对越差.

当模型取上述值时,通过对本文模型进行求解可知, 最优维修成本率C*随最优维修次数N*的变化如图3所示,最优维修成本率C*随最优维修次数N*的增加先增加而后减小.最优维修次数N*=5时,维修成本率取最小值,C*=9.67 (元/h),此时对应的最优预防性维修周期依次为x1=248.68 h,x2=168.11 h,x3=133.17 h,x4=110.46 h,x5=92.69 h.若对元动作单元采用完美更换策略,其他参数同上,得到最优维修成本率为C*=12.06 元/h,最优维修周期为248.68 h.由此可见,在一个更新周期内,采用完美更换策略的成本率更高,本研究的维修策略更优.若不考虑预防性维修对本质疲劳类和损伤类故障影响的差异,即取e=1,f=0,其他参数不变.求得最优维修成本率C*=8.70 元/h, 最优维修次数N*=8.70,对应的最优预防性维修周期依次为x1=251.98 h,x2=175.69 h,x3=142.23 h,x4=119.93 h,x5=101.94 h,x6=86.10 h,x5=71.72 h.由此看出,若没有考虑元动作单元存在的本质疲劳类故障,预防性维修效果被高估,得到的最优维修策略的预防性维修次数偏高,维修成本率偏小.

图3 最优维修成本率随最优维修次数的变化

维修成本是制定维修策略的一个重要影响因数,不同类型维修成本的变化可能会导致最优维修策略的改变.下面讨论各类型维修成本的变化对最优维修策略及最优维修成本率的影响.

表1 损伤类故障最小维修成本对最优维修策略的影响

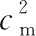
表2 本质疲劳类故障最小维修成本对最优维修策略的影响

表3结果表明,随着cp的增加,C*逐渐增加.但当cp接近更换成本cr时,这时直接采取更换策略(N*=1),C*保持在12.06 元/h;N*随着cp的增加而减小.通过减小预防性维修次数,节省维修成本从而降低维修成本率.当cp接近更换成本cr时,直接采取更换策略,N*=1保持不变;更新周期长度随着cp的增加而呈现减小的趋势.这是因为cp较高时,最小维修成本就相对越低,可适当缩短更新周期降低总体的维修成本率.但当cp接近更换成本cr时,直接采取更换策略(N*=1),更新周期长度保持不变.

表3 预防性维修成本cp对最优维修策略的影响

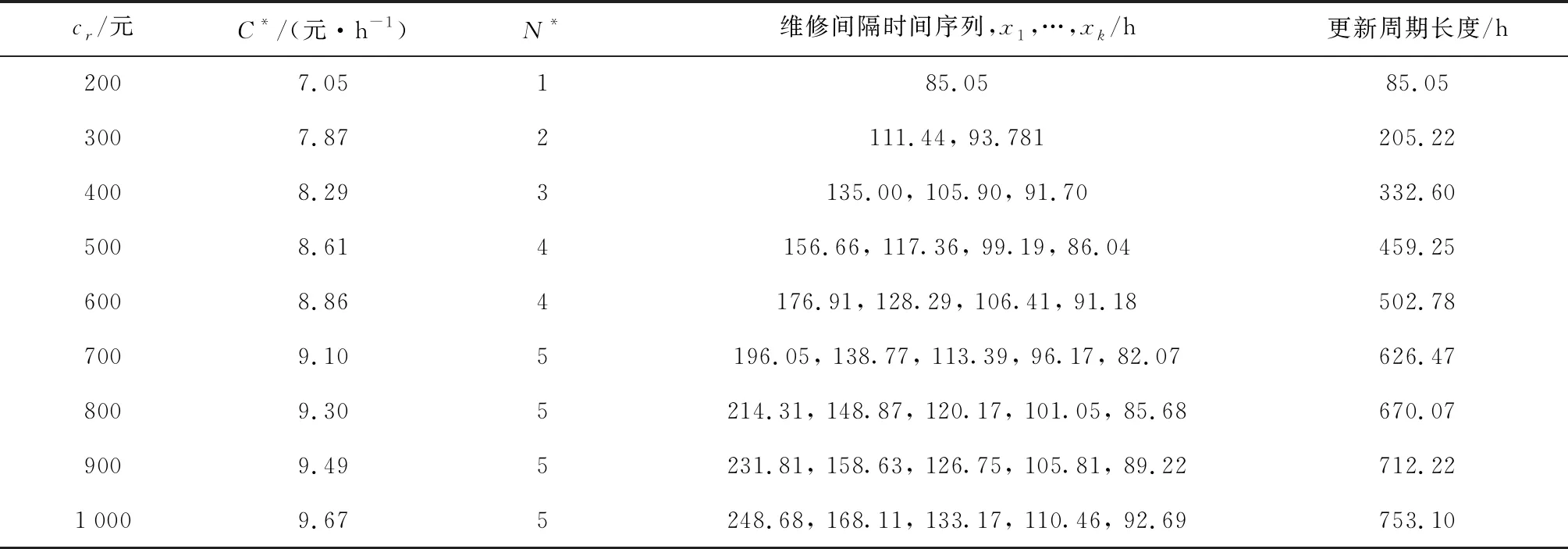
表4 更换成本cr对最优维修策略的影响

不同元动作单元损伤类故障与疲劳类故障比例不尽一致,下面讨论故障比例因子变化对最优维修策略的影响.在其他参数不变的情况下,调整故障比例因子e和f,得到的结果如表5所示.

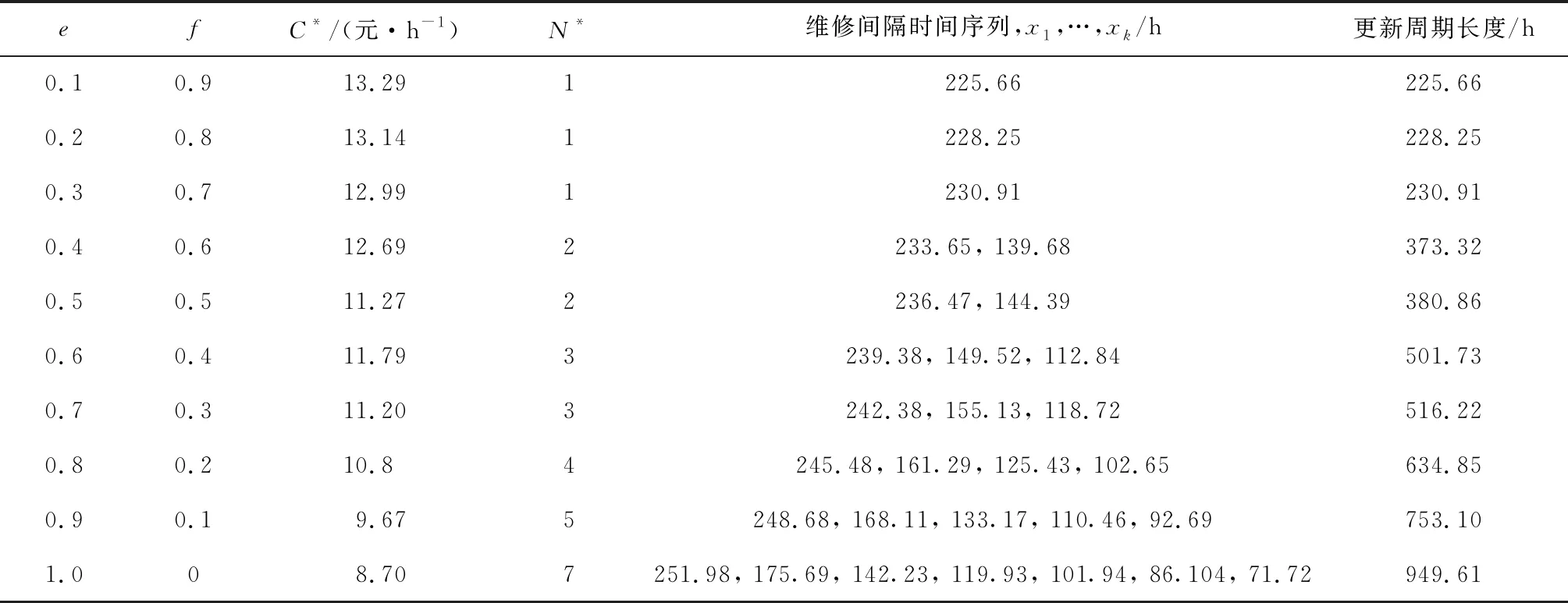
表5 故障比例因子对最优维修策略的影响

预防性维修效果参数ak对最优维修成本率和最优维修策略可能存在影响,在本算例中,ak是由调整因子ν决定的.因此,下面讨论调整因子ν的变化对最优维修策略的影响.在其他参数不变的情况下,变动调整因子ν,得到的结果如表6所示.

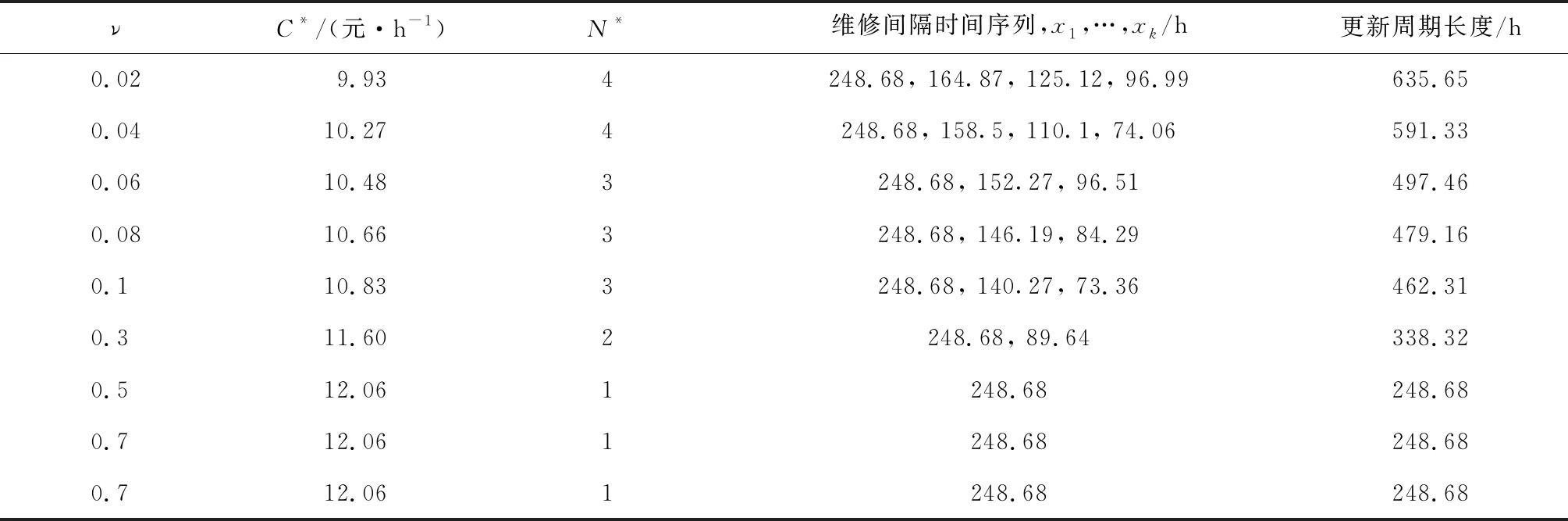
表6 调整因子ν的变化对最优维修策略的影响

表6结果表明,随着ν的增加,C*逐渐增加,但当ν增加到一定值后,C*保持不变.这是因为,预防性维修效果随着ν的增加而变差,在相同条件下故障发生的次数增多而导致维修成本率增加.当ν增加到一定值时,预防性维修效果已经非常差,直接对元动作单元进行更换效果更好,这时C*保持在12.06 元/h不变;N*随着e的增加而呈现减小的趋势,更新周期长度随着e的增加而减少,但当ν增加到一定值后,N*和更新周期都保持不变.这是因为随着预防性维修效果变差,适当减少预防性维修次数、缩短更新周期可以减少维修成本率.当ν增加到一定值时,对元动作单元直接更换的维修方式成本效益更佳,因而N*和更新周期不再随e的增加而变化.

6 结论

基于GGP,考虑预防性维修对损伤类和本质疲劳类故障维修效果的差异,建立了元动作单元的顺序预防性维修优化模型,并分析了各类型维修成本、故障比例因子以及调整因子对最优维修决策的影响,研究结果表明:

(1) 相比更换维修策略,本文模型得到的预防性维修策略的维修成本率更低.

(2) 不考虑预防性维修对不同类型故障维修效果的差异会低估元动作单元的维修成本率,得到不准确的维修策略.

本文虽然取得了一定的成果,但依然存在一些不足:模型中没有考虑维修时间,这可能会影响模型的精度;只考虑了单个元动作单元的预防性维修策略,对多个元动作单元的维修策略有待进一步研究.