自由落体状态下二维结构物砰击载荷计算

孙 哲, 眭旭鹏, KOROBKIN Alexander 邓彦增, 张桂勇, 宗 智, 姜宜辰

(1. 大连理工大学 船舶工程学院,辽宁 大连 116024; 2. 东安格利亚大学 数学学院,英国 诺维奇 NR47TJ; 3. 中国空气动力研究与发展中心 计算空气动力研究所,四川 绵阳 621000)

在现如今的船舶与海洋工程领域,对于多体船或者剖面曲率很大的船舶,较大的航行速度会使船体受到很大的砰击力,这会导致十分严重的结构损伤甚至发生海上事故[1].因此,砰击现象的研究对于船舶和海洋结构物的性能以及强度具有重要的意义.

砰击入水的开创性工作可以追溯到von Karman[2]和Wagner[3]对于楔形体入水过程的研究.基于经典Wagner模型,众多学者对其进行了不同程度的发展和完善.Dobrovol’skaya[4]研究了具有自由液面流体的相似流动,并提出了入水砰击问题的数学积分表达式.在Zhao等[5]的模型中,自由液面是线性的而物体边界和伯努利方程保持非线性.Cointe等[6]、Howison等[7]和Oliver[8]通过匹配渐近展开法将整个流场分成3部分并进行了深入的研究.段文洋等[9]提出了通过辅助线来构建在流动分离发生后的虚拟物体表面,以便快速地预报砰击力.除了对于楔形体的一系列研究,Tassin等[10]对抛物线物体的入水模型开展研究,而Korobkin[11-12]则研究了具有任意形状物体的入水过程.

试验方法是研究砰击过程的特征以及验证解析理论模型的重要手段[13],其中楔形体是被研究最多的模型.典型的研究工作包括Panciroli等[14-15]对刚性和弹性对称楔形体的砰击过程进行试验和计算.近年来,众多学者对楔形体的倾斜砰击入水以及非对称楔形体的砰击入水进行了试验[16-18].对于更复杂的船体结构,比如船艏部分,Aarsnes[19]所进行的自由落体试验是其后数值方法验证[20-21]中引用最多的研究成果之一.

如今,数值模拟方法以数据可靠、计算速度快等特点成为砰击基础理论研究和实际应用中最常用的工具.边界元法(BEM)是最早应用于砰击模拟的数值方法之一,比如Sun[20]、Bao等[22]和Wu等[23]的研究工作.尽管在数值模拟中可以考虑自由液面的非线性效应和流体的黏度,但计算成本过高使其并不适用于海洋结构物设计的初期.

目前的解析理论研究大多数集中在匀速入水或控制入水.然而,在这种情况下物体所受的砰击力可能会与其在自由落体入水情况下所受的砰击力大不相同.同时,自由落体入水情况更适用于实际工程领域中的结构强度评估.此外,虽然数值模拟方法同样能够应用于结构物自由落体砰击入水的模拟,但解析理论模型更易于从物理学的角度分析砰击力的组成和特性,在时间成本方面解析理论模型相较于数值模拟方法更具有明显的优势,同样也能避免在数值模拟的过程中进行网格划分操作或者物理模型选取不当带来的主观误差.尽管大多只适用于流动分离之前的砰击入水阶段,但是目前的解析理论模型依旧是工程领域预报结构物砰击入水初期阶段的运动响应以及砰击力峰值最有效率的工具.

鉴于上述背景,将时域上的精细积分法与砰击力计算的解析理论模型相结合,将物体的运动控制方程转换为一组常微分方程组,在提升计算精度和减少计算时间的同时,对二维结构物在砰击过程中的砰击载荷进行研究.

1 砰击入水的解析理论模型

1.1 理论基础

本文使用的解析理论模型均基于势流理论,即流体被视为不可压缩且无黏流体.由于砰击是一个在极短时间内发生的高速动态过程,所以可以合理忽略流体的重力对于物体砰击过程的影响[24-25].同时,流体的表面张力也被忽略.

图1 二维对称物体砰击示意图

t时刻物体表面任意一点的垂向坐标可表示为

z=f(y)-ξ(t)

物体关于z轴对称,因此其湿表面在y轴上的投影长度是2c(t),其中c(t)可以由Wagner条件[11, 25]计算得到:

(1)

流体动力学采用基于平板撞击假设的Wagner理论[3]进行求解,计算区域由物体湿表面在y轴上的投影和未受扰动的自由液面构成.流体的速度势函数φW可通过如下控制方程和边界条件求解:

(2)

式(2)的解φW(y,0,t)可表示为

(3)

-c≤y≤c

1.2 砰击压力计算

物体沿着湿表面的压力分布是通过伯努利方程计算的:

式中:φ(y,z,t)为z≤0区域的速度势函数;ρ为液体的密度.在基于Wagner理论的不同砰击解析理论模型中,通过不同的近似方法处理非线性效应和湿表面形状来计算物体所受的压力.

(1) 经典Wagner模型(OWM)[26-27].

在OWM中,仅考虑伯努利方程的线性项,将速度势函数式(3)代入,得到压力表达式:

(2) 基于非线性伯努利方程的Wagner模型(WN)[26].

在WN模型中,考虑了伯努利方程的非线性项,同样将速度势函数式(3)代入,得到压力表达式:

(3) Logvinovich模型(OLM)[25,28].

在OLM中,在考虑了非线性项的同时,将压力的计算放置在物体浸没深度所处的平面上(即z=-ξ(t)), 而不是在未受扰动的自由液面上.同时,将速度势函数φ表示为Wagner解φW(y,0,t)在z=0处的泰勒展开式,并将式(2)中的第3个方程作为边界条件.于是,速度势函数φ可以改写为

物体沿湿表面的OLM压力计算公式可最终表示为

p(y,t)=

(4) 改进的Logvinovich模型(MLM)[25].

在MLM中,Korobkin[25]提出通过考虑物体的形状来进一步提高OLM的计算精度,即抛开之前的平板碰撞假设,使压力的计算在真实的物体湿表面上进行.与OLM的处理方法类似,速度势函数φ也表示为φW(y,0,t)在z=0处的泰勒展开式,并将式(2)中的第3个方程作为边界条件.于是,速度势函数φ可以改写为

物体沿湿表面的MLM压力计算公式可最终表示为

式中:fy为f函数对y的导数.

(5) 广义Wagner模型(GWM)[25].

在GWM中,速度势和压力的计算放置在物体和流体交界高度附近的物体湿表面上,其余对于速度势φ函数的处理与MLM一致.于是,速度势函数φ可以改写为

φ(y,t)≈φW(y,0,t)+(f(y)-f(c(t)))×

物体沿湿表面的GWM压力计算公式可最终表示为

1.3 砰击力计算

在物体砰击过程中,作用在物体上的砰击力是通过沿物体湿表面对其所受的压力进行积分获得的.不过,压力表达式中的速度相关项包含了一个奇异项,1/(c2-y2), 这使得在y=c附近压力变为负值且不可积分[27].根据Korobkin[25]的建议,这一速度相关项的砰击压力应在区域-c*≤y≤c*进行积分,其中c*是距y=c处最近且满足pv(c*,t)=0的点.

对于具有任意形状的物体,其形状函数可以表示为物面上均匀分布的离散点的线性差值,如下式所示:

(4)

之后,根据1.2节所述各个解析理论模型的压力计算公式和式(4),逐个对分段进行积分,便可得到物体所受的砰击力.

为了描述物体在砰击入水过程中的运动状态,借助牛顿第二定律并对其进行改写:

(5)

式中:m为物体的质量;g为重力加速度,本文取9.81 m/s2;Fv和Fa分别为组成物体所受砰击力FH的两部分,Fv为速度v的相关项,Fa为加速度a的相关项,

(6)

(7)

pv为物体所受砰击压力中的速度相关项部分;pa为物体所受砰击压力中的加速度相关项部分;av1、av2、aa1和aa2为砰击力系数.对于不同的解析理论模型,av1、av2、aa1和aa2的表达式各不相同,如表1所示.表中:

表1 不同理论模型下的砰击力系数

2 时域上的精细积分法

在计算获得物体所受的砰击力Fv和Fa之后,物体的动力学控制方程,即式(5),可以通过精细积分法[29]进行求解.在精细积分法中,动力学控制方程可重新表示为

(8)

M=m+ρaa1

G=ρav1

K=0

接着,引入一个新的相空间变量:

v=[ξζ]T

其中ζ表示为

于是,式(8)可进一步表示为

(9)

f=[0r]T

对于式(9)所描述的物体动力学系统,若已知第k个时间步的变量vk,则下一个时间步中的变量vk+1可通过如下所示的Duhamel积分得到:

vk+1=exp(Hη)vk+

(10)

式中:η为时间间隔.

在时域上使用精细积分法求解物体运动特征的关键在于计算指数矩阵exp(Hη).该计算包含了两个步骤.首先,使用指数矩阵的附加定理将矩阵扩展为如下形式:

exp(Hη)=exp(Hδ)m,δ=η/m,m=2N

(11)

通常选择20作为N的取值,于是应用附加定理之后的时间间隔δ可被视为一个非常小的值,因此前4阶泰勒展开式可以用来作为exp(Hδ)的表达形式:

exp(Hδ)≈I+R

R=Hδ+(Hδ)2/2!+(Hδ)3/3+(Hδ)4/4!

(12)

将式(12)代入式(11), exp(Hδ)可近似表示为

exp(Hη)=(I+R)2N=(I+2R+R2)2N-1

(13)

为了避免由于I的值远大于Rn的增量而导致计算精度的下降,并不是直接对式(13)连续地进行平方,而是使用下式来表征增量的部分:

在重复N次上述操作后,指数矩阵exp(Hδ)最终可以表示为

exp(Hη)=I+RN

如式(10)所示,为了得到第k+1个时间步中的变量vk+1,还需要确定f的值,而这可以通过“预估-校正”的方法获得.方法的具体细节详见文献[30].

3 结果与讨论

3.1 模型验证

首先验证精细积分法在砰击问题上的时间收敛性.选取5个不同的时间步长Δt并结合MLM模拟了一个二维楔形体的自由落体砰击过程.楔形体的半宽为0.11 m、底升角为25°.加速度随时间变化的预报结果如图2所示,当时间步长小于 0.000 1 s 后,所得结果几乎没有差异.因此,对于之后的所有模拟,均使用 0.000 1 s 作为时间步长.

图2 基于MLM模型的时间步长收敛性验证

接着,将1.2节所述的各类解析理论模型与精细积分法相结合,研究楔形体在砰击过程中的运动状态.具体而言,将上文所述形状的楔形体置于3个不同的高度处,使其进行自由落体运动.在此,定义物体初始入水速度为v0,则这3个不同初始高度对应的物体初始入水速度分别为v0= 2.2,3.1,3.6 m/s.在本文中,所研究的物体均为二维物体,因此取楔形体的单位长度质量为2.125 kg/m.预报楔形体在砰击过程中加速度随时间的变化,并将所得结果与文献[14]中的实验结果进行对比,对比结果如图3所示.

观察图3可以发现,OWM给出了与其他4种模型相比过高的预测值,这与文献[14, 25]中所指出的现象相一致.而其他考虑了非线性因素或物体表面影响的模型得到了更加准确的预报结果,尤其是MLM和GWM.当v0= 2.2,3.1 m/s时,MLM预测的加速度峰值与实验结果基本一致,而当v0= 3.6 m/s时,非线性模型预测的加速度峰值较试验结果高出10%～20%.

为了检验该方法是否适用于形状更加复杂的二维剖面,选取如图4所示的船体剖面模型进行验证.同样地,选取3个不同的高度使其进行自由落体运动,对应的入水速度分别为v0= 0.61,1.48,2.43 m/s.船体剖面的单位长度质量为261 kg/m.将不同解析理论模型得到的垂向砰击力F随时间变化的预报结果与Aarsnes[19]的试验结果以及Sun[20]的BEM数值模拟结果进行对比,对比结果如图5所示.

图4 船体剖面示意图

观察图5可以发现,虽然在入水初期,解析理论模型与试验以及BEM得到的结果吻合良好,但如果湿表面到达船体剖面上部的末端, 即当c等于剖面半宽之后,解析理论模型便不再能够预报流体和船体剖面的运动变化.然而,砰击理论指出,砰击力会在流体发生流动分离之后立刻达到峰值,这意味着解析理论模型能够相对可靠地预报砰击过程中物体所受的砰击力峰值的大小.对于不同模型的计算结果,OWM依然明显地过度预测了垂向砰击力,而其他模型的结果更接近Aarsnes[19]的试验结果和Sun[20]的BEM结果.总体来说,如同上文根据楔形体模型得到的推论一致,对于所有的工况,MLM提供了最准确的预测.

3.2 自由落体状态下的砰击力特性研究

解析理论模型的优点之一是易于研究砰击过程中主要的影响因素和物理机理.Korobkin[31]通过解析方法研究了椭圆抛物线物体在自由落体状态下的砰击载荷和运动状态变化,Scolan等[32]通过研究发现,无论是在二维模型还是三维模型,当物体的入水速度恒定,流体能量在砰击过程中会均匀地传递到抬升与飞溅的液体中.在本节中,研究物体在自由落体状态下所受砰击力的特性,即砰击力和物体浸没深度之间的关系.

其中:系数Av和Aa是浸没深度ξ的函数, 即Av=Av(ξ),Aa=Aa(ξ).

对于砰击水动力在物体所受的流体载荷中占主导地位的情况,即对于轻质物体或具有较大入水速度的物体,物体自身的重力可以合理地忽略不计.因此,通过系数Av和Aa,便可以将自由落体状态下物体的动力学方程式(5)重新表述为

(14)

之后,式(14)可以进一步表示为

(15)

(16)

Av=ξCv

(17)

Aa=ξ2Ca

(18)

式中:Cv和Ca为两个仅与楔形体底升角有关的常数.在OWM中,Cv和Ca可通过下式计算得到:

而在MLM中,Cv和Ca的表达式非常复杂,具体形式可参照Korobkin等[33]的研究成果,这里不再赘述.通过对式(16)的两侧在时域上进行积分,物体在砰击入水过程中的速度[31]可表示为

(19)

之后,将式(19)代入式(14)或式(15),便可得到物体的加速度表达式:

进一步地,加速度绝对值的最大值|ξ|max可表示为

|ξ|max=

(20)

观察式(20)可以发现,在不考虑物体重力的情况下,对于指定底升角的楔形体,其在砰击入水过程中最大加速度或砰击力峰值发生的浸没深度由质量决定,而不受初始入水速度的影响(假设楔形体在此浸没深度之前不会发生流动分离).

选取半宽为0.11 m,底升角分别为β= 15°,25°,35° 的二维楔形体模型作为研究对象,使用MLM计算了其从不同的高度处在自由落体状态下的砰击过程,并预报了物体加速度随浸没深度的变化.在计算过程中,物体自身的重力忽略不计.不同下落高度所对应的物体初始入水速度分别为v0= 2.2,3.1,3.6 m/s.同时,针对不同底升角的楔形体模型,选取了两个不同的单位长度质量进行研究,分别为2.125和8.5 kg/m.

计算所得到的结果如图6所示,其展示的结果与式(20)一致,即虽然物体在砰击过程中最大加速度或砰击力峰值的数值会随初始入水速度改变,但是其所对应的浸没深度却与初始入水速度无关.此外,在砰击入水过程中,物体的加速度或受到的砰击力会随着底升角的减小或者自身质量的增大而减小.

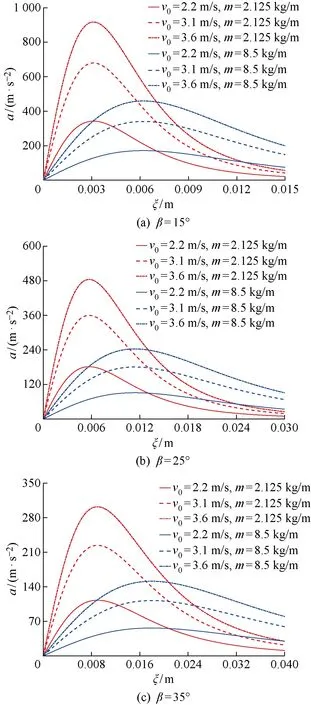
图6 自由落体状态下楔形体的加速度变化

不过随着物体质量的增加或者初始入水速度的减小,物体自身的重力相较于所受到的砰击水动力不再是小量.此时,忽略物体重力会导致计算结果存在误差.若以5%作为误差的阈值来判断预报计算结果的准确性,则针对每一个不同底升角的楔形体模型,依据其质量和初始入水速度绘制能够忽略物体自身质量的临界曲线.在此,物体单位长度质量的研究范围选取为0.05～50 kg/m,各楔形体模型的临界曲线如图7所示.从展示的结果来看,随着物体质量或者底升角的增大,满足误差要求的临界初始入水速度也随之增大.

图7 各楔形体模型的临界曲线

不过,对于任意复杂形状的物体,不同于上述研究的楔形体模型,很难再从式(15)得到类似式(19)这样的简单表达式,因为式(17)和式(18)不再是必要的.然而,通过对式(16)进行多次分部积分,可以得到:

(21)

(22)

观察式(22)可以发现,上述对于楔形体的结论对于任意复杂形状的物体仍然适用,即在忽略物体重力的情况下,最大加速度或砰击力峰值对应的浸没深度仅与物体的质量和形状相关.

选择半宽均为0.11 m的两个不同形状的曲线楔形体作为验证此结论的模型,其中一个为凸面形状,另一个为凹面形状,模型的具体构型如图8所示.与上述方法类似,在整个砰击入水的过程中,物体同样处于自由落体状态,物体的单位长度质量分别取2.125和8.5 kg/m,物体初始入水速度分别为v0= 2.2,3.1,3.6 m/s,选择MLM进行预报物体加速度随浸没深度的变化,同时不考虑物体自身的重力.

图8 曲线型楔形体形状示意图

计算所得到的结果如图9所示,所得到的结论与前文对于楔形体模型的分析一致,即虽然最大加速度或砰击力峰值的数值取决于物体的初始入水速度,但是其发生的浸没深度却与初始入水速度无关.此外,对比图8中3类不同形状楔形体所得的结果可以发现,剖面的肥瘦程度在很大程度上会影响物体加速度(或砰击力)和加速度峰值(或砰击力峰值)所对应的浸没深度.剖面越“肥胖”,物体加速度或砰击力越大,加速度峰值或砰击力峰值越早来临.

图9 自由落体状态下曲线型楔形体的加速度变化

对于此类曲线形状的物体,不同于楔形体模型,增大物体质量或者减小初始入水速度并非会使得计算结果的误差单调增加,因此绘制出能够忽略物体自身质量的临界曲线十分困难.于是,在此仅给出“物体的初始入水速度需要大于1 m/s”作为能忽略物体自身质量的近似前提条件.

4 结论

采用基于势流理论的砰击解析理论模型,研究了自由落体条件下任意二维对称剖面在砰击过程中的动力学特性.使用了几种典型的解析理论模型,从经典Wagner模型到更复杂的MLM和GWM等.

为了求解物体在自由落体状态下的运动状态,将精细积分法与解析模型相结合,并在时域上进行积分.若二维剖面的形状为复杂的曲线形状,那么该物体的表面则通过在物面上生成均匀离散的点并在点与点之间进行线性插值进行处理.

之后,选取两种不同的二维模型,即楔形体和船体剖面,将按照上述方法得到的结果与现有文献中的试验和其他数值模拟结果进行了对比.对比结果表明,考虑非线性因素和湿表面形状的解析理论模型通常能够得到更为精确的结果,尤其是MLM.不过解析理论模型固有的局限性使其无法分析流体在发生流动分离之后的动态变化,但这些模型仍然可以正确地预报流动分离发生前物体所受的砰击力峰值.

此外,对于在砰击过程中可以忽略物体重力的情况,即对于轻质物体而言,砰击力占其所受水动力载荷的主要成分,如果保证物体在自由落体入水过程中产生的最大加速度或砰击力峰值发生在流体发生流动分离之前,那么物体在最大加速度或砰击力峰值发生时的浸没深度仅仅由物体的形状和质量有关,而与其初始的入水速度无关.