“平均数、中位数与众数”的知识点辨析

朱绍文

平均数、众数、中位数都是描述一组数据集中趋势的量，但它们的定义、求法以及描述的角度和适用的范围又不尽相同，同学们常常将它们弄混淆.那么在具体问题中，应采用哪个量来描述一组数据的集中趋势呢？下面对它们的特征及正确的适用范围进行分析说明.

一、定义不同

平均数：平均数的大小与一组数据里每个数据都有关系，其中任何数据的变动都会引起平均数的变动.因此，平均数能较充分地反映一组数据的“平均水平”，但它容易受极端值的影响.

中位数：中位数的大小仅与数据的排列位置有关，将一组数据按从小到大的顺序排列后，最中间的数据或最中间两个数据的平均数为中位数.因此，部分数据变动对中位数没有影响，当一组数据中的个别数据变动较大时，一般用中位数来描述“平均水平”.

众数：众数着眼于各数据出现的次数，其大小与该组的部分数据有关，求一组数据的众数既不需要计算，也不需要排列，只要找出该数据中出现次数最多的数据即为众数.因此，当一组数据中有不少数据重复出现时，一般用众数来描述“平均水平”.

例1  现有7名同学测得某大厦的高度如下：（单位：m ）

29.8  30.0  30.0  30.0  30.2  44.0  30.0

（1）在这组数据中，中位数是____众数是____，平均数是____;

（2）凭经验，你觉得此大厦大概有多高？ 请简要说明理由.

解析：（1）将这组数据按从小到大的顺序排列，即 29.8，30.0，30.0，30.0，30.0，30.2，44.0，由于排在中间的数据有一个，即30.0，所以中位数是30.0；出现次数最多的数有一个，即 30.0出现了 4次，所以众数是30.0.

这组数据的平均数（29.8 + 30.0 +

30.0 + 30.0 + 30.0 + 30.2 + 44.0）=32.0 ；

（2）凭经验，大厦高约32.0 m.

原因是数据44.0误差太大或测量错误，从而导致平均数的数值偏大，因此按照中位数和众数来确定.

二、求法不同

1.求平均数

計算平均数，由于数据的情况各不相同，可以分三种方法：

（1）当数据较少或较小，且没有重复出现时，用公式计算较为简便.

例2  数据10，9，8，7，4，2，3，1的平均数是（    ）.

A.4.5    B.5    C.5.5    D.6

解：（10 + 9 + 8 + 7 + 4 + 2 + 3 + 1） = 5.5.

故应选C项.

（2）当一组数据中出现重复数时，用加权平均数公式计算简便，即 n

其中分别叫做的权，且

例3  在一次体检中，测得八年级（1）班第一小组10名同学的身高情况是：有2人是 145cm，3 人是 148cm，4 人是 156cm，1 人是 160cm，则这10位同学的平均身高是（    ）.

A.150.8cm    B.151cm

C.151.8cm    D.152cm

解：（145×2 +148×3 +156×4+160） =151.8 cm，

故应选C项.

（3）当数据较大、较多且在某一个常数a，附近摆动时，用公式 a求解比较容易.其中是原数据与a的差组成的新数据的平均数.

例4  求下列数据的平均数;71，69，72，74，66，65，70，73.

解：取常数a=70，原数据的每一个数减

去 70，得到一组新数据：1，-1，2，4，-4，-5，0，3.

2.求中位数

求一组数据的中位数，应先将这组数据按由小到大（或由大到小）的顺序排列，然后再分数据的个数是奇数还是偶数求出中位数：当数据的个数是奇数时，则处于正中间位置的数就是这组数据的中位数；当数据的个数是偶数时，则正中间两个数据的平均数就是这组数据的中位数.

例5  10名工人某天生产同一零件的件数是 15，17，14，10，15，19，17，16，14，12，求这一天10名工人生产零件的中位数.

解：将所给的10个数按从小到大的顺序排列得：10，12，14，14，15，15，16，17，17，19，最中间的两个数据都为15，它们的平均数也是15，则这组数据的中位数是15 （件）.

3.求众数

确定一组数据的众数，首先找出这组数据中的各数据出现的次数，其中山现次数最多的数据就是众数.

例6  在一次数学考试中，10名学生的得分如下;70，90，100，90，80，100，90，50，80，80，求这次数学考试得分中的众数.

解：在这一组数据中，100分出现2次，90分出现3次，80分出现3次，70分出现1次，50分出现1次，故80分和90分是这组数据的众数.

三、适用范围不同

平均数是最常用的一个代表值.它充分利用了全部数据的信息，计算方便，但易受极端值的影响.当数据中有极端值时，平均数的代表性较差.这时，选择中位数作为“平均水平”的代表要更好，在一组数据中不大于或不小于中位数的数据各占50% .中位数常用来描述“中间位置”或“中等水平”等.它受极端值影响较小，但没有充分利用所有数据的信息，而且当数据较多时不便于计算.当描述同类产品中哪个品牌错量最大、同学中哪个年龄的人最多、进行民意调查或选举时，人们最

关心的是出现次数最多的数据，即众数.但众数可能不惟一，而且当各数据出现的次数大致相同时，众数的意义不太明显.

1.当用样本估计总体时，一般采用平均数

例7  小新家今年6月份头6天用米量如下表：

请你运用统计知识，估计小新家6月份 （按30天算）用米量为______千克.

解：这6天的平均每天用米量为

≈0.833.

则6月份用米量为

25.0 （千克）.

2.当一组数据中有“异常数”（一组數据中值过大或过小的数据通常被称为“异常数或异常值”）时，一般采用中位数或众数描述这组数据的一般水平.因为有异常数据，其平均数可能相差较大.

例8  据报道，某公司的33名职工的月工资（以元为单位）如下：

（1）求该公司职工月工资的平均数、中位数、众数;（精确到个位数）

（2）假设副董事长的工资从5000元提升到20000元，董事长的工资从5500元提升到 30000元，那么新的平均数、中位数、众数又是什么？（精确到个位数）

（3）你认为哪个统计量能反映这个公司员工的工资水平？结合此问题谈一谈你的看法.

解：（1）平均数为

≈1500+591=2091（元）.

中位数是1500元，众数是1500元.

（2）平均数为

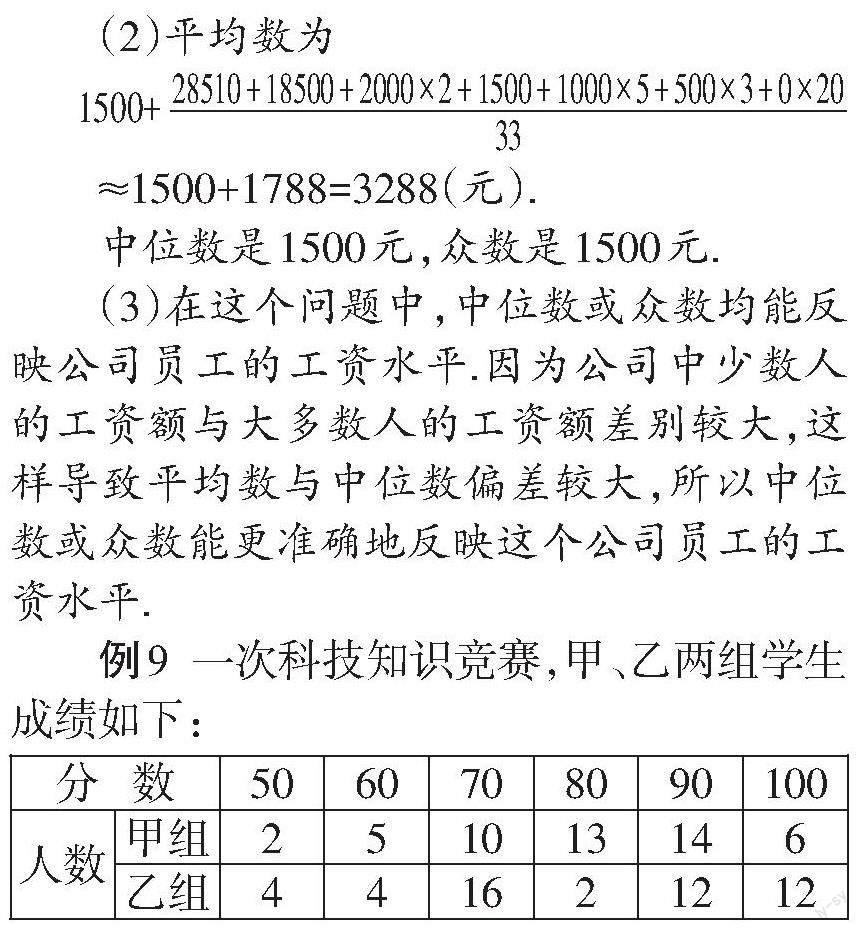
≈1500+1788=3288（元）.

中位数是1500元，众数是1500元.

（3）在这个问题中中，位数或众数均能反映公司员工的工资水平.因为公司中少数人的工资额与大多数人的工资额差别较大，这样导致平均数与中位数偏差较大，所以中位数或众数能更准确地反映这个公司员工的工资水平.

例9  一次科技知识竞赛，甲、乙两组学生成绩如下：

已经算得两组都有50人，平均分都是80

分，请根据你所学过的统计知识，进一步判定这两个组的学生在这次竞赛中的成绩谁优谁次，请说明理由.

解：我们从多角度来综合考虑这个问题：

（1）甲组成绩的众数是90分，乙组成绩的众薮是70分，从成绩的众数比较看，甲组成绩好些.

（2）甲、乙两组成绩的中位数都是80分，甲组成绩在中位数以上（包括中位数）的有33 人，乙组成绩在中位数以上的有26人，从这一角度看甲组成绩总体较好.

另外，我们还可以从高分段人数进行考虑，从成绩统计看：甲组成绩高于80分的人数为14+6=20（人），乙组成绩高于80分的人数为12+12=24（人），所以，乙组成绩集中在高分段的人数多，同时乙组得满分的人也要多些，从这一角度看，乙组成绩较好.