基于衰减速率算法模型的压力容器裂纹缺陷剩余寿命与安全裕度
李炎炎,何 磊,龙 伟,王喆灏
(四川大学 机械工程学院,四川 成都 610065)
压力容器广泛应用于空气动力技术试验、国防工业、核电工业、化学工业、海洋工程等领域,在国民经济中具有举足轻重的地位[1-3]。但压力容器属于具有高易燃易爆风险的特种装备,一旦发生失效,便会造成重大的人员伤亡和经济损失。因此,压力容器的安全评估方法一直是设备安全评估领域关注的重点以及研究热点[4-5]。
裂纹疲劳是导致压力容器安全失效的主要原因。工程应用领域中,判定压力容器裂纹缺陷安全状态主要采用双判据失效评定图法[6-8],该方法能够判别含缺陷结构的潜在失效模式,并且能进行结构的脆性断裂、弹塑性断裂和塑性失稳分析,因此被广泛地应用于压力容器和压力管道的断裂安全状态的评定中[9]。工程中,常用射线法或平行线法计算裂纹缺陷安全裕度。其中:射线法假定裂纹缺陷在稳定疲劳载荷的作用下,裂纹失效的安全评定点在失效评定图上会沿着直线匀速移动直至失效[10]。平行线法则基于模糊隶属度分区思想,将失效评定图划分为不同安全程度的区域[11]。研究表明[12-15],裂纹缺陷的安全衰减路径为一条具有时变性的曲线。然而,由于缺乏对裂纹缺陷失效速率时变性的考虑,这些方法仅能表示是否安全或者模糊地评定安全程度,并不能准确地表征压力容器的安全程度[16]。
毛志辉等[17]提出的安全衰减路径在理论上可以估算缺陷失效路径上任何点位的动态剩余寿命,能真实反映设备的动态安全程度,也能据此较为准确地评估和预测缺陷和设备的续用寿命,这是与传统静态安全评定方法的最大不同之处,且该理论已在压力容器裂纹缺陷安全评定方面有较多应用,能够准确反映压力容器动态安全裕度的评估。因此,本文在安全衰减路径理论的基础上,建立一种能够反映裂纹缺陷失效速率时变性的安全衰减速率表征模型,并基于此提出了曲线积分形式的压力容器裂纹缺陷剩余寿命预测模型与安全裕度表征模型。
1 传统安全评估方法
1.1 失效评定图法
失效评定图法是一种用于判定压力容器平面裂纹缺陷安全性的常规方法[18]。该方法由两个独立的安全判定坐标轴构成。其中,横坐标载荷比Lr为裂纹缺陷的塑性失稳程度,纵坐标断裂比Kr为裂纹缺陷的脆性断裂程度[19]。该方法对裂纹缺陷的安全性评定主要是基于Kr与Lr组成的失效评定曲线(FAC)实现的[20],其原理如图1[9]所示。当评定点的参数坐标(Lr,Kr) 位于 FAC曲线的安全区范围内时,当前裂纹缺陷处于安全状态;若评定点的参数坐标处于 FAC曲线的安全区范围之外,则意味着裂纹缺陷已经无法满足安全要求[21-22]。由图1可见,评定点1在安全区内,表明评定点1的裂纹缺陷仍然处于安全状态,压力容器可以正常使用;而评定点2在非安全区内,表明压力容器已无法正常使用。

图1 失效评定图法[9]Fig.1 Failure assessment chart method[9]
1.2 射线法
射线法是表征和计算压力容器裂纹安全裕度计算的主要方法,其原理如图2[10]所示。由图2可见,若以评定点1为例,以坐标原点O为端点过裂纹缺陷安全评定点A作一条射线,与失效评定曲线FAC相交于B,AB与OB之间的长度比即为此裂纹缺陷的安全裕度;若以评定点5为例,则CD与OC之间的长度比为此裂纹缺陷的安全裕度。
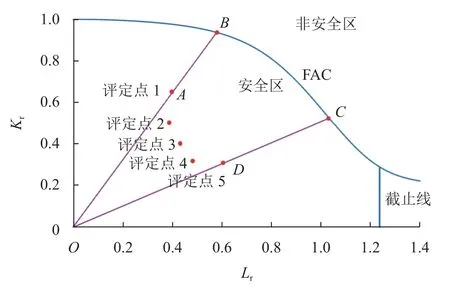
图2 射线法[10]Fig.2 Radiographic method[10]
射线法模型是在“直线路径”与“匀速衰减”两个假定前提下建立的。直线路径指裂纹缺陷在稳定疲劳载荷的作用下,其安全评定点在失效评定图上会沿着直线OB接近FAC;匀速衰减指裂纹缺陷在稳定疲劳载荷的作用下,其安全评定点沿着OB的移动速率是均匀的[9]。由此可得安全裕度M表征公式为:
式中,lAB和lOB分别为线段AB和OB的长度。
1.3 平行线法
平行线法是在概率断裂力学与失效评定图的基础上形成的裂纹缺陷安全裕度表征方法,其主要原理是通过对FAC曲线作平行曲线将失效评定图划分为绝对安全区、十分安全区、比较安全区、一般安全区和非安全区[11]。通过观察裂纹缺陷评定点坐标(Lr,Kr)所处的区域来估算裂纹缺陷的安全裕度。图3为用平行线法表征裂纹缺陷安全裕度的示意图[11]。
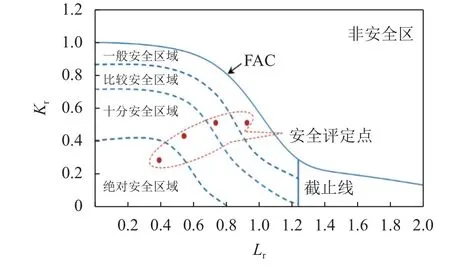
图3 平行线法[11]Fig.3 Parallelogram method[11]
2 安全衰减速率算法相关模型
2.1 裂纹缺陷的安全衰减路径
裂纹在疲劳扩展过程中,其评定点在失效评定图上由安全域到非安全域的滑移轨迹被称为压力容器裂纹缺陷的安全衰减路径[23]。图4为压力容器裂纹缺陷的安全衰减路径的计算流程示意图。
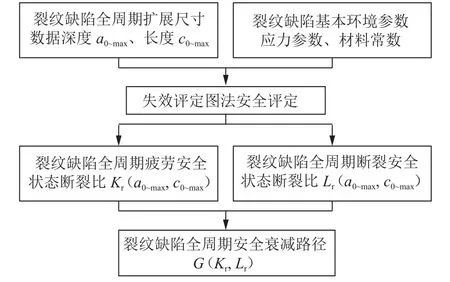
图4 安全衰减路径计算流程图Fig.4 Flowchart for the calculation of safe attenuation paths
图5为表面裂纹缺陷的安全衰减路径,图像数据源自文献[11]。通过图5中的点位变化可以发现,裂纹缺陷安全评定点越接近失效边界FAC,则缺陷安全点的衰减速率就越快[24-25]。由此可见,传统射线法不能表征压力容器裂纹缺陷安全衰减速率的时变性,因而从射线法理论得出的裂纹缺陷安全裕度与剩余寿命计算结果是极不准确的。
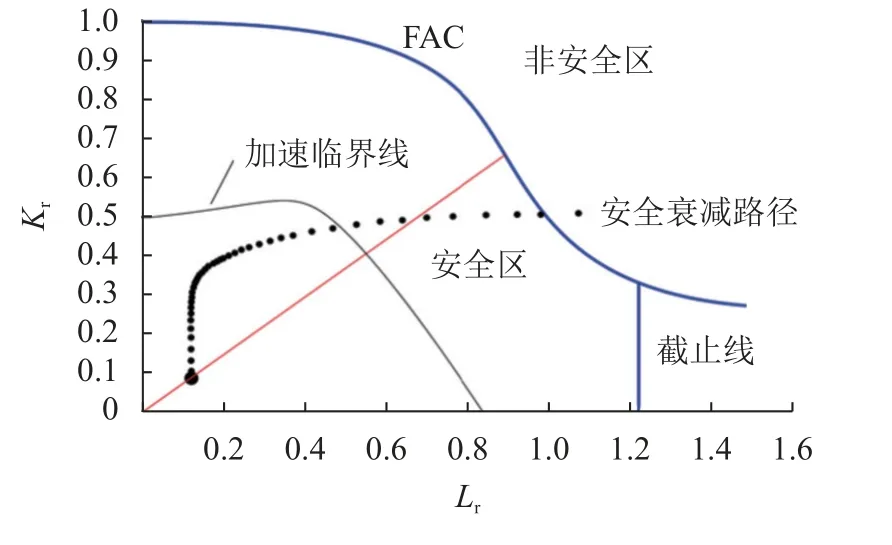
图5 表面裂纹缺陷的安全衰减路径[11]Fig.5 Safe attenuation paths for surface crack defect[11]
2.2 安全衰减速率与剩余寿命计算模型
为了对裂纹的安全衰减速率进行量化表征,基于图5中裂纹安全评定点在失效过程中的固有规律,将裂纹缺陷的安全衰减速率P定义为裂纹缺陷安全评定点沿着安全衰减路径靠近失效评定曲线FAC的移动速率。由于速率模型的建立需要具备时间参考系,考虑到裂纹安全评定点的失效过程是由疲劳载荷的累积作用引起的,选用疲劳载荷对裂纹缺陷的累积作用频次n作为安全衰减速率的时间参考系。由此可得安全衰减速率计算公式为:
通过安全衰减速率与安全衰减路径的数学关系来推导裂纹缺陷的剩余寿命计算模型,图6为安全衰减速率与安全衰减路径之间的数学关系示意图。
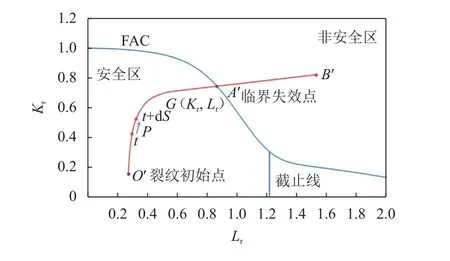
图6 安全衰减速率与安全衰减路径的关系示意图Fig.6 Schematic of the relationship for safe decay rate and safe attenuation paths
假定图6为某裂纹缺陷的安全衰减路径曲线,图中O′为裂纹缺陷的初始点,B'为裂纹崩溃终点,A′为裂纹缺陷的临界失效点,选取安全衰减路径O'~A'段上的任意一点t进行分析。假定缺陷在t点的安全衰减速率为P,定义裂纹缺陷安全评定点到临界失效点之间的曲线路径为S,由安全衰减路径与安全衰减速率在t点瞬时数值关系可得,微分变量 dn与 dS之间的数学关系表达式为:
取图6中安全衰减路径的O'~A'段作为第一类曲线积分的积分路径定义为全安全域积分路径Go′~A′,取t~A'段作为第一类曲线积分的积分路径定义为剩余安全域积分路径Gt~A′,并对式(3)两侧进行曲线积分可得:
由曲线积分的定义可知,式(4)等号左侧的计算结果等于安全衰减路径在t~A'段的累积应力循环次数,由此可得裂纹缺陷的剩余寿命计算公式为:
整理后可得裂纹缺陷剩余寿命的通用计算模型为:
式中,P(n)到P(Lr,Kr)的换算过程中的裂纹缺陷沿深度和长度方向的动态尺寸扩展数据a(n)与c(n),可根据《在用含缺陷压力容器安全评定(GB/T 19624—2019)》[18]进行转换。
2.3 安全衰减速率的差分形式
尽管在第2.2节中给出了裂纹缺陷安全衰减速率的数学理论模型,但由于疲劳载荷的累积作用频次n为正整数形式的离散变量。因此,在使用式(2)计算裂纹缺陷的安全衰减速率时,需要对其进行差分处理。对式(2)进行差分计算可得安全衰减速率模型的差分形式,如式(7)所示:
安全衰减速率差分形式的计算精度主要是由Δn的取值决定的。 Δn的取值越小,计算精度就越高。令Δn趋向于1,可以得出任意一次疲劳载荷作用时的安全衰减速率计算表达式为:
2.4 安全裕度的表征模型
因为裂纹缺陷安全评定点到临界失效点之间的曲线路径S以及与之关联的安全衰减速率P反映了缺陷的安全程度,也就是说:裂纹缺陷的安全裕度M既与曲线路径S相关,也与安全衰减速率P相关。M与S和P、n、裂纹扩展速率V的这种关联性,可以用S-V关系曲线的路径速度积来表示。图7为利用龙伟团队[12-15,23-25]提出的路径速度积分方法计算裂纹缺陷安全裕度的示意图。

图7 表面裂纹的S-V关系曲线[25]Fig.7 S-V relationship curve for surface crack defect[25]
设图7(b)为图7(a)中裂纹缺陷的安全衰减速率与安全衰减路径之间的关系函数f(S,V),裂纹缺陷在图7(a)中的初始安全点O′、当前评定点t、临界失效点A′的安全衰减速率分别对应图7(b)中的初始速率点VO′、当前速率点Vt、临界失效速率点VA′,缺陷的安全域路径速度积为U,剩余路径速度积为Un。由S-V的函数关系可知,安全域路径速度积分U为:
剩余路径速度积Un为:
通过图7(b)以及U与Un之间的数学关系可得裂纹缺陷的安全裕度M的路径速度积分表征模型为:
M=Un/U(11)
尽管文献[11]给出了安全裕度计算方法的构建思路,但并没有给出关于f(S,V)具体计算方法。为了构建出安全裕度M的具体数学形式,用图6中的安全衰减速率P来替代式(9)和(10)中的安全衰减速率概念关系式f(S,V),将积分方式由图7(b)中的平面积分 dN替换为图6中的曲线积分 dS,并用图7(a)中安全衰减路径上的初始安全点O′、当前评定点t以及临界失效点A′构成的全安全域积分路径Go′~A′和剩余安全域积分路径Gt~A′来替代式(9)与式(10)在图7(b)中对应的积分范围,可得到基于本文安全衰减速率模型的安全裕度计算式为:
3 实例验证与对比
通过与文献[26]中的疲劳试验基本数据对比,对所提方法进行试验验证,实验基本流程如图8所示。
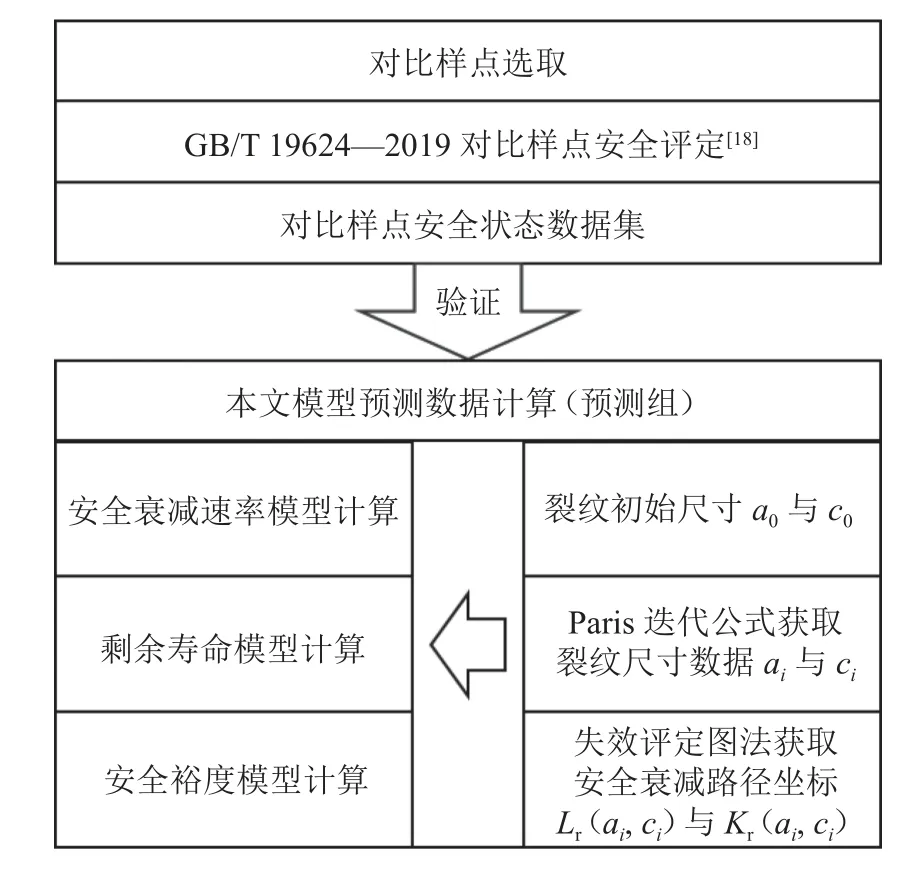
图8 实验验证基本流程图Fig.8 Basic flowchart for experimental validation
3.1 实验流程与实验数据
从文献[26]中选择2组疲劳裂纹拉伸实验数据对本文方法进行验证,试件基本参数见表1。
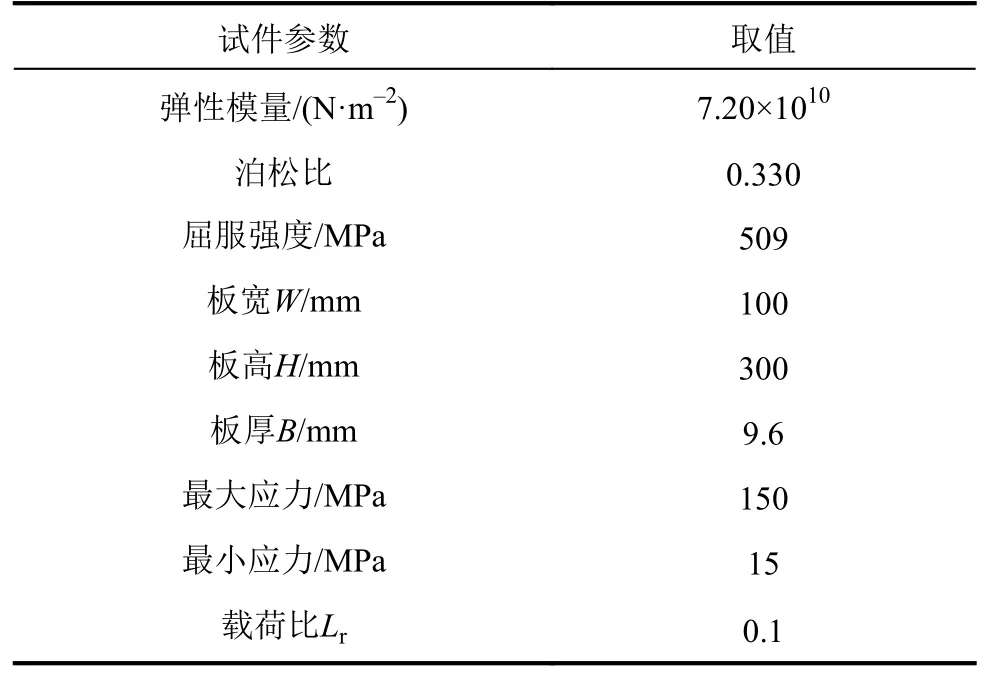
表1 试件样板的力学性能、样板尺寸与应力环境Tab.1 Mechanical properties, sample size and stress environment of test specimen
裂纹初始尺寸与载荷加载次数见表2。表2中,试件1与试件2分别为原文献中试件PCA6与PCA15。试件外观与应力加载方式如图9所示。图9中,a与c分别为裂纹深度和长度。

表2 文献[26]中2组裂纹缺陷的基本数据Tab.2 Basic data on 2 sets of crack defects in the literature [26]
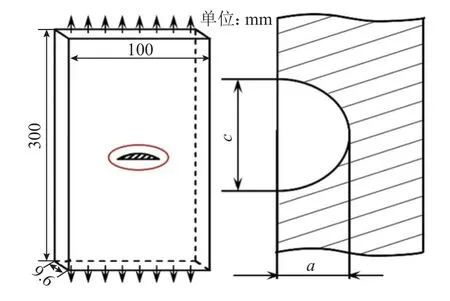
图9 试件外观与应力加载方式Fig.9 Appearance of the specimen and the manner of loading the stresses
3.2 数据计算
对裂纹缺陷的安全裕度与剩余寿命进行预测时,采用Paris疲劳扩展公式[27]对裂纹缺陷在疲劳载荷作用下的深长尺寸扩展数据进行计算。由于压力容器的周向尺寸要远大于厚度尺寸,裂纹缺陷沿长度方向扩展速率的计算可进行适当的修正,以避免裂纹缺陷深度方向的安全评价结果过于保守[18]。因此,本文使用文献[18]中的Paris修正扩展速率公式来计算试件裂纹缺陷的深长尺寸:
式中:裂纹缺陷沿长度方向的扩展速率修正系数为0.9;ai与ci分别为第i次载荷作用后的裂纹深度与长度; ΔKa与 ΔKc分别为裂纹缺陷在深度方向与长度方向的应力强度因子变幅;C和m均为材料常数,均可由实验测得,其数值与材料种类以及载荷环境有关[28-30]。表3为试件的Paris材料常数。

表3 试件的Paris材料常数Tab.3 Paris material constants for specimens
分别将试件1与试件2的裂纹初始深度a0和初始长度c0,以及裂纹在深长尺寸端点处的应力强度因子变幅 ΔKa与 ΔKc代入式(13),可得裂纹缺陷深长尺寸的Paris迭代数据。裂纹缺陷深长尺寸扩展实验的原始数据以及用文本方法得到的Paris迭代数据如图10所示。

图10 裂纹缺陷深长尺寸扩展数据Fig.10 Deep and long dimensional extension data for crack defects
由图4的失效评定流程和图10中的裂纹尺寸数据可得图11中试件1与试件2的安全衰减路径。图11中,相邻评定点的应力循环次数间隔为500次,各安全评定点的坐标 (Lr,Kr)依据《GB/T 19624—2019》[18]中表面裂纹失效评定图法进行计算。
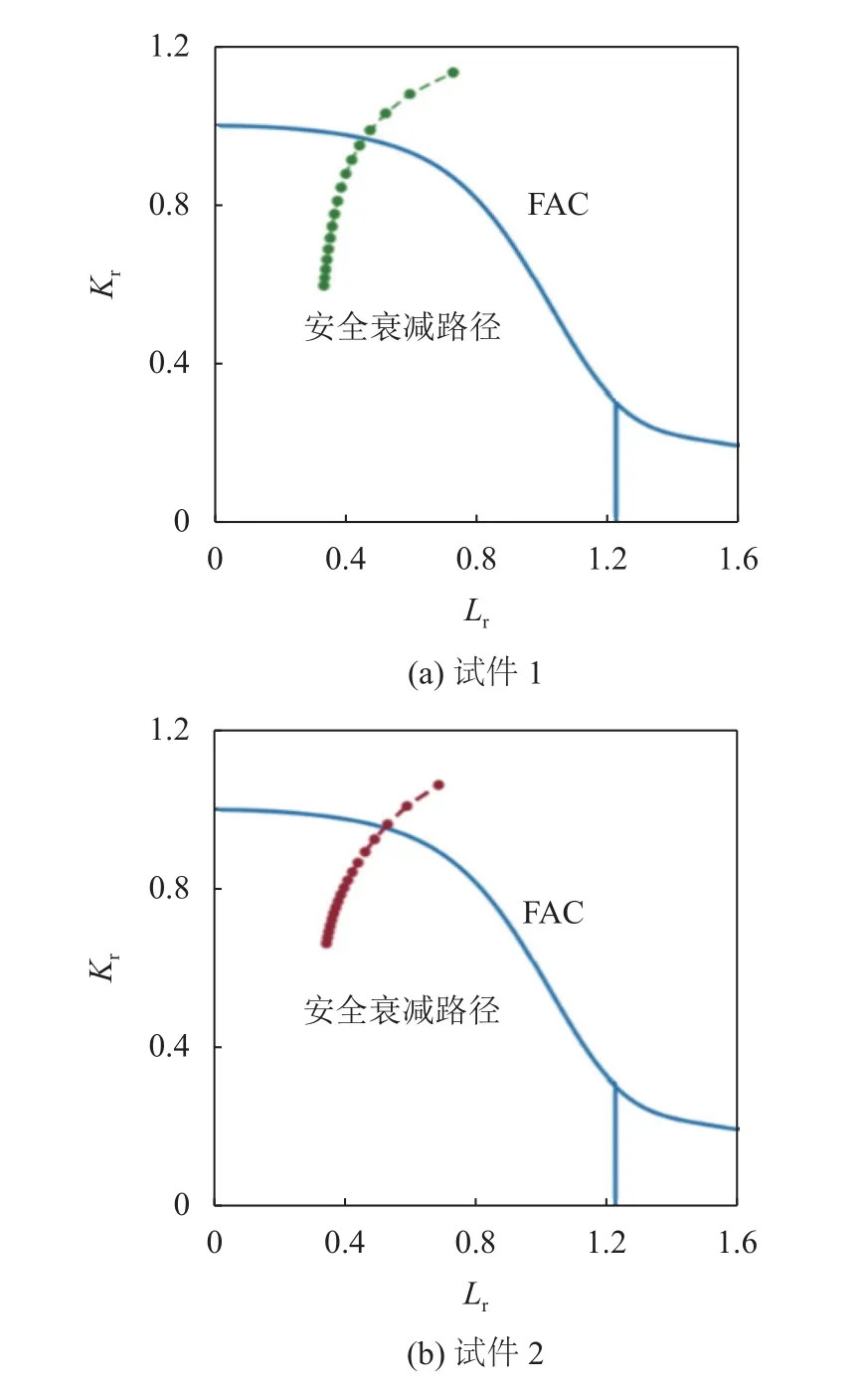
图11 裂纹缺陷的安全衰减路径Fig.11 Safe attenuation paths for crack defect
将图11中的数据代入到式(7)可得两组裂纹缺陷的安全衰减速率曲线。通过图10与图11点位的对应关系可以将安全衰减速率的P(n)形式转换为P(Lr,Kr)形式,如图12所示。
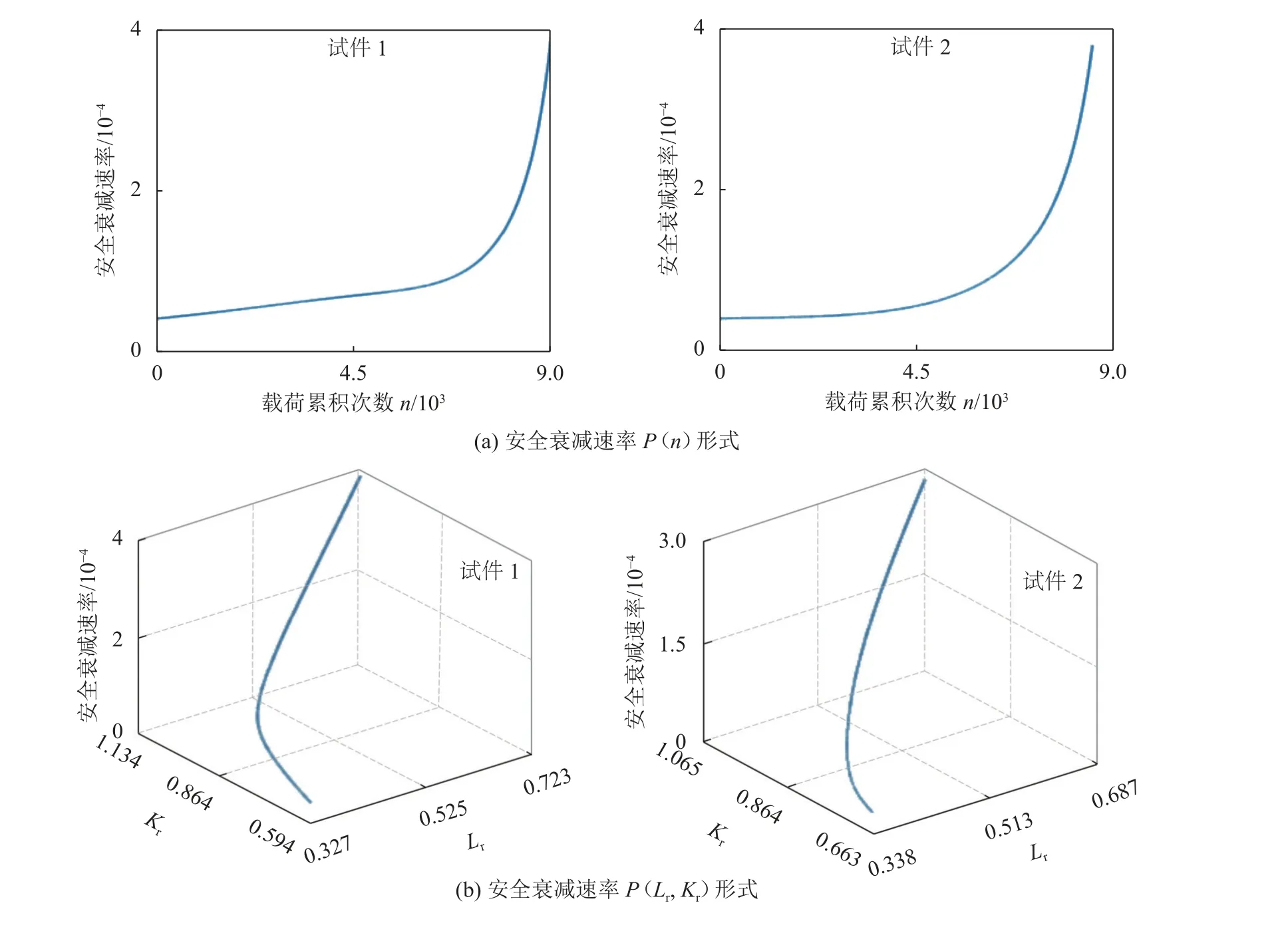
图12 裂纹缺陷的安全衰减速率Fig.12 Safe decay rate for crack defect
通过图12中安全衰减速率的曲线模型可知,裂纹缺陷的后期失效速率要明显快于前期失效速率。由此可见,安全衰减速率表征模型与压力容器裂纹缺陷的实际安全衰减情况十分吻合。通过将图11中的安全衰减路径数据与图12中的安全衰减速率P(Lr,Kr)形式代入到式(6)和(12),得到裂纹缺陷失效前任意评定点的剩余寿命以及安全裕度。
3.3 剩余寿命模型的实验验证
文献[26]裂纹缺陷真实剩余寿命是通过国家标准《在用含缺陷压力容器安全评定》GB/T 19624—2019[18]的评定流程获得的,测试样点的裂纹缺陷的初始尺寸与载荷循环次数见表4。图13为本文方法的剩余寿命预测曲线。

表4 文献[26]中两组裂纹缺陷的初始尺寸与载荷循环次数Tab.4 Initial size and number of load cycles for two groups of crack defects in the literature [26]
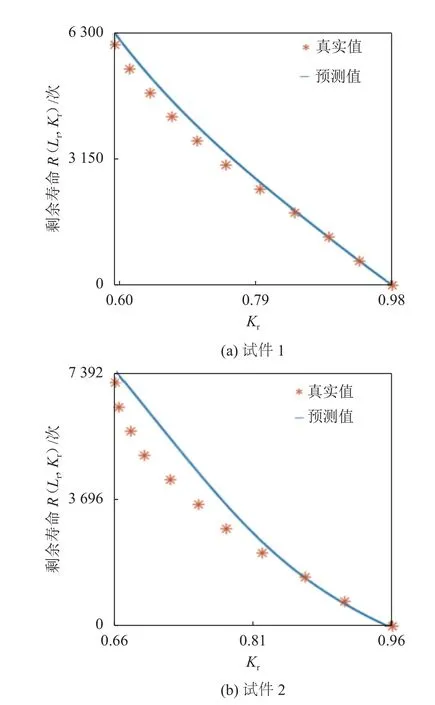
图13 剩余寿命预测结果与真实数据对比Fig.13 Comparison of predicted results with real data for residual life
由图13可见,所提方法的剩余寿命预测曲线与表4中样点的真实剩余寿命十分接近。试件2在前期的预测误差相对较大,这主要是由图10中试件2前期的裂纹迭代尺寸与真实数据差异较大引起的。
3.4 安全裕度模型的对比
将本文所提压力容器安全裕度表征模型与传统射线法模型、平行线法模型进行对比。对比数据来自表4中的样点数据,射线法模型采用式(1),平行线法的评定图源自文献[10],本文安全裕度模型采用式(12)。图14为利用射线法与本文方法计算样点0~10的安全裕度结果。表5为3种方法的安全裕度计算结果对比,表5中,平行线法使用的安全裕度等级符号的含义为:Ⅳ(绝对安全)、Ⅲ(十分安全)、Ⅱ(比较安全)、Ⅰ(一般安全)、0(不安全)。
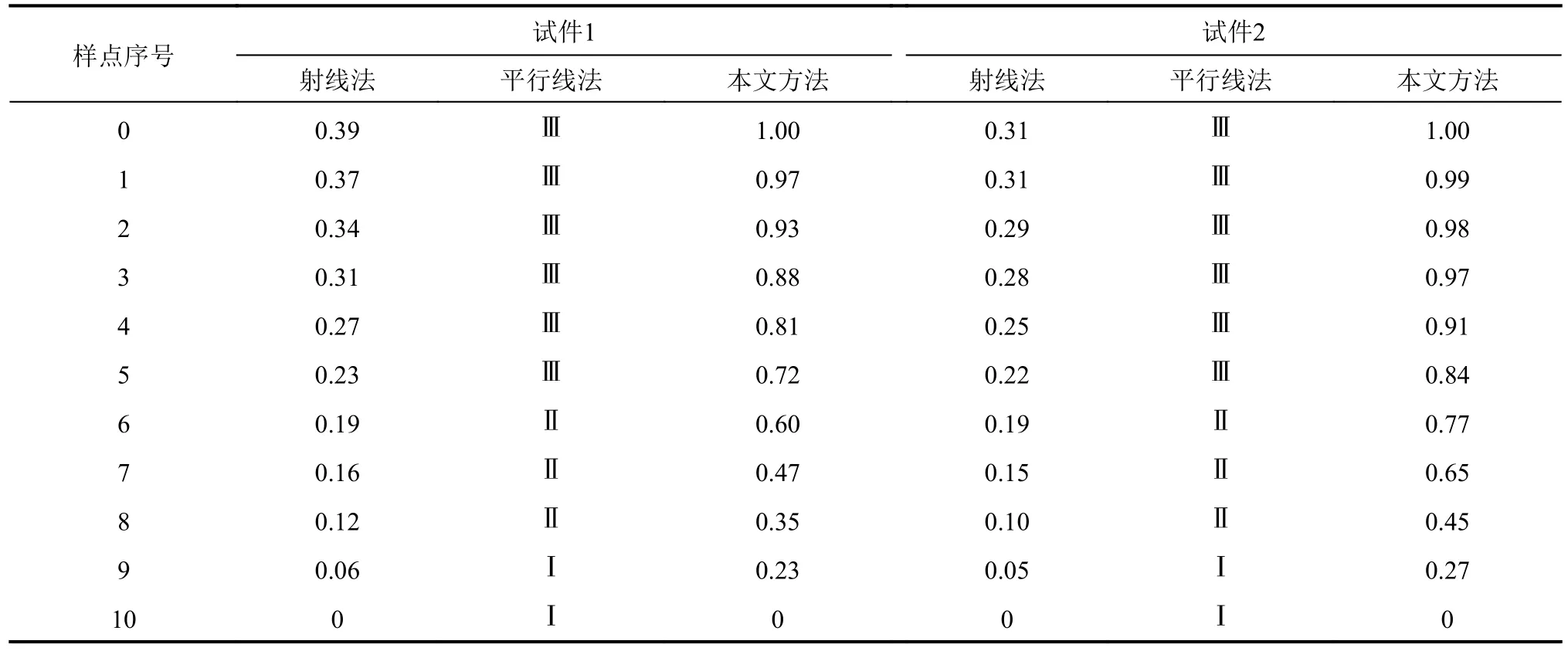
表5 3种方法对样点安全裕度计算的结果对比Tab.5 Comparision of results on safety margin calculations for sample points by three methods

图14 安全裕度评定结果对比Fig.14 Comparison of safety margin evaluation results
由表5可见,3种安全裕度表征方法的评价结果与裂纹缺陷安全裕度的衰减趋势基本一致。射线法与所提方法的安全裕度表征模型会随着裂纹实际安全裕度的下降而变小,而平行线法对应的则是安全等级由Ⅳ到Ⅰ的阶梯式衰减。平行线法的主要缺陷在于对裂纹缺陷安全裕度缺乏量化的评定结果,导致其对裂纹缺陷的真实安全状态难以判定。例如,当试件1被评定为Ⅲ级安全状态时,其裂纹缺陷的真实安全状态既可能是测试样点0,也可能是测试样点5。从表4的数据上来看,两者的剩余寿命数值差异巨大。
与平行线法相比,射线法能够对裂纹缺陷的安全裕度进行量化表征,而且安全裕度的衰减过程也比较平缓。由表5与图14可知,射线法缺陷在于对裂纹初期的安全裕度评价过于保守。由表5中两组裂纹缺陷的初始安全裕度数据可知,射线法算得两组裂纹缺陷初始状态的安全裕度表征数值分别为0.39和0.31。但从表1和表2的数据可知,两组裂纹缺陷的初始深度仅占板件总壁厚的20%。由此可见射线法模型存在不足之处。
与上述两种方法对比,本文方法计算出的裂纹缺陷安全裕度更加符合裂纹缺陷的实际安全衰减过程。当裂纹缺陷的剩余寿命维持在总寿命的50%以上时,所提方法的安全裕度下降速率较为缓慢;而当裂纹缺陷的剩余寿命处于50%以下时,安全裕度的下降速率会迅速增加。这种安全裕度表征方式不仅与裂纹缺陷的疲劳扩展规律相一致,而且也有利于安全检测人员对临近失效裂纹缺陷进行识别与检测。综上所述,本文所提安全裕度表征方法要明显优于传统安全裕度表征方法。
4 结 论
本文以压力容器裂纹缺陷的安全衰减路径理论为依据,通过结合S-V路径速度积思想,构建了路径速度积分方法的曲线积分形式,提出了一种能够反映裂纹缺陷疲劳失效速率时变性的安全衰减速率表征模型,探索了裂纹缺陷在疲劳载荷作用下的安全失效规律。
本文建立了安全衰减路径以及安全衰减速率之间的数学关系式,提出了一种全新的曲线积分形式的剩余寿命预测模型与安全裕度表征模型。结果表明,本文所提寿命预测模型的计算结果与裂纹缺陷的实际剩余寿命十分接近;所提安全裕度表征模型不仅更加符合裂纹缺陷的实际安全衰减过程,而且更加有利于安全检测人员对临近失效裂纹缺陷的识别与检测。

