轻质多材料重载自动引导车总成优化设计

孙 鸿，李启慧，傅海龙，彭 浩*

(1.南京工业大学 机械与动力工程学院, 江苏 南京 211800；2.华晓精密工业（苏州）有限公司, 江苏 苏州 215000)

以自动引导车（AGV）作为载具的智能化运输方式，能提高生产力、减少输送错误、节约劳动成本、提高过程安全性，在智能仓储系统中具有无可替代的核心地位，AGV已成为柔性制造领域的重大刚性需求[1]。目前，国内的AGV生产商以中、轻载为主，重载AGV的开发尚处于探索阶段。而在航空航天、港口船舶、特大型工程等经常需要调度大型、重型设备的行业中，重载AGV高效及敏捷的操作是解决其中长久存在的输送、配合问题的有效手段，吸引了学术及工业界的广泛关注[2]。现有的重载AGV存在重量大、耗能高的问题，若能对重载AGV进行车身总成优化设计，并在其关键承载部件中选择性应用轻质材料，则可以在保证工程安全的前提下降低重载AGV的重量并节约能源消耗，间接降低制造成本，推广其在智能产线中的使用。

优化方法方面，针对连续体的拓扑优化决定了材料在设计域内的最佳空间分布，已被成功应用于航空航天[3-4]、增材制造[5]、建筑工程[6]、车辆制造[7]等领域，其目的是优化结构受力和材料配置，实现轻量化设计以节约制造成本。渐进结构法（ESO）由Xie等[8-9]于1993年提出，该方法将初始结构划分为单元，逐步删去低效单元使得结构受力更加均匀。渐进结构法计算简单，易于实现，发展迅速，Huang等[10]在此基础上提出双向渐进结构法（BESO），在逐步删去低效单元的同时，在高效单元附近生成单元以使结构更快趋于优化。才琪等[11]将能量原理及满应力设计准则与BESO法结合，使之适用于桁架结构优化设计，结果表明，采用该方法的基结构优化结算结果与解析解误差小于1%。程自然等[12]基于ESO法对碟式聚光器进行多层次优化设计消除棋盘格现象，之后提取了拓扑结构的特征线，随后沿特征线确定截面尺寸，新结构重量降低了34.4%且自重下最大形变无显著变化。Bahramian等[13]使用BESO算法对承受轴向载荷的薄壁方管进行了拓扑优化，以提高其耐撞性能，结果显示，在牺牲不到3.5%的能量吸收的情况下，重量减少了16.21%，压碎力峰值提高了35.67%；因此，研究者认为该算法在大变形和面外屈曲下设计薄壁结构方面具有很高的潜力。

轻质材料方面，碳纤维增强树脂基复合材料（CFRP）因其优异的综合性能不断加速普及应用，对其力学性能[14]、成型工艺[15]、异种材料连接[16]等方面的研究均有拓展。由于具有高比强度、高比模量，低比重及优异的抗疲劳性能，CFRP成为轻量化设计中理想的材料，在全球范围内需求量与使用量均逐年提升。然而，铺层角度、厚度和形状极大影响了CFRP构件成型后的力学性能。王庆等[17]对CFRP设计的保险杠进行了拉丁超立方采样、Kriging近似建模技术与遗传算法优化求解，研究结果表明，在满足碰撞性要求后，CFRP保险杠有效减重36.4%。Liang等[18]模拟、制造并实验验证了不同层数、不同纤维方向的CFRP起落架，研究表明，当承受垂直载荷时，铺层为[0]12（0°铺层重复12次）的方案展现出较高强度，铺层为[0/90]6（0°和90°铺层重复6次）的方案其次，[0/90/45/-45/90/0]对称铺层（从上至下铺层角度依次为0°、90°、45°、-45°、90°、0°）则具备更好的纵向应变。Ma等[19]针对汽车下曲轴箱提出工艺与结构一体化优化方法，以铺层厚度、形状和顺序为变量，纤维以初始角度[45/-45/0/90]5进行堆叠，并在Optistruct solver软件中求解，研究表明，与金属油底壳相比，CFRP油底壳减重率达66%。综上所述，重载AGV存在发展时间较短与普及速度较快的双重特征，现有的承载部件制造大多依托于经验设计，存在较大的优化空间。此外，目前重载AGV优化设计研究中以CFRP作为轻质替换材料的研究较少。

本文首先基于BESO法对重载AGV承载车架及舵轮安装板分别进行拓扑优化，得到满足实际工程需要的车身总成结构。其次，使用真空辅助树脂传递模塑（VARTM）工艺制备CFRP试样进行力学性能实验，计算得到其性能参数。随后针对纤维初始角度为[0/45/90/-45]的CFRP进行铺层角度优化。最后，在软件COMSOL Multiphysics 5.6中，针对新车身总成进行有限元分析，求解特征频率及对应模态，验证优化结果，建立从材料到结构的完整重载AGV轻量化设计流程。

1 物理模型

由于承载以及输送要求，重载AGV一般采取对称设计和多舵轮组共同驱动，以达到承载平衡、无需转弯半径的目的，各轮间通过转速和旋向的配合即可实现AGV的全方位运动[20]。单个驱动承载单元由车架结构及舵轮安装板两部分组成，AGV关键承载部件如图1所示。

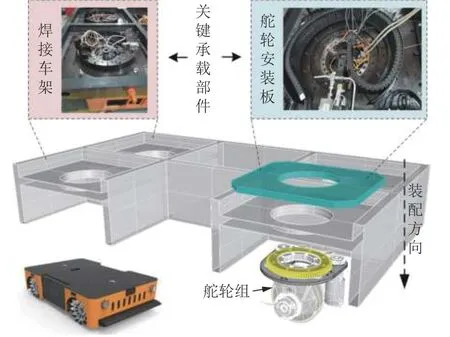
图1 AGV关键承载部件Fig.1 Key load-bearing components of AGV

舵轮安装板正上方铺设盖板，使承载式AGV上表面平齐，同时与车架形成类似桥台与支撑梁的结构。盖板往往薄而可拆卸，在简化受力模型中排除盖板，直接受力于车架。驱动机构与舵轮安装板为螺纹连接，因此，设置螺纹孔周围为非设计区域，支撑面为舵轮安装板与驱动机构的接触面。重载AGV车架及舵轮安装板的初始拓扑优化模型如图2所示。

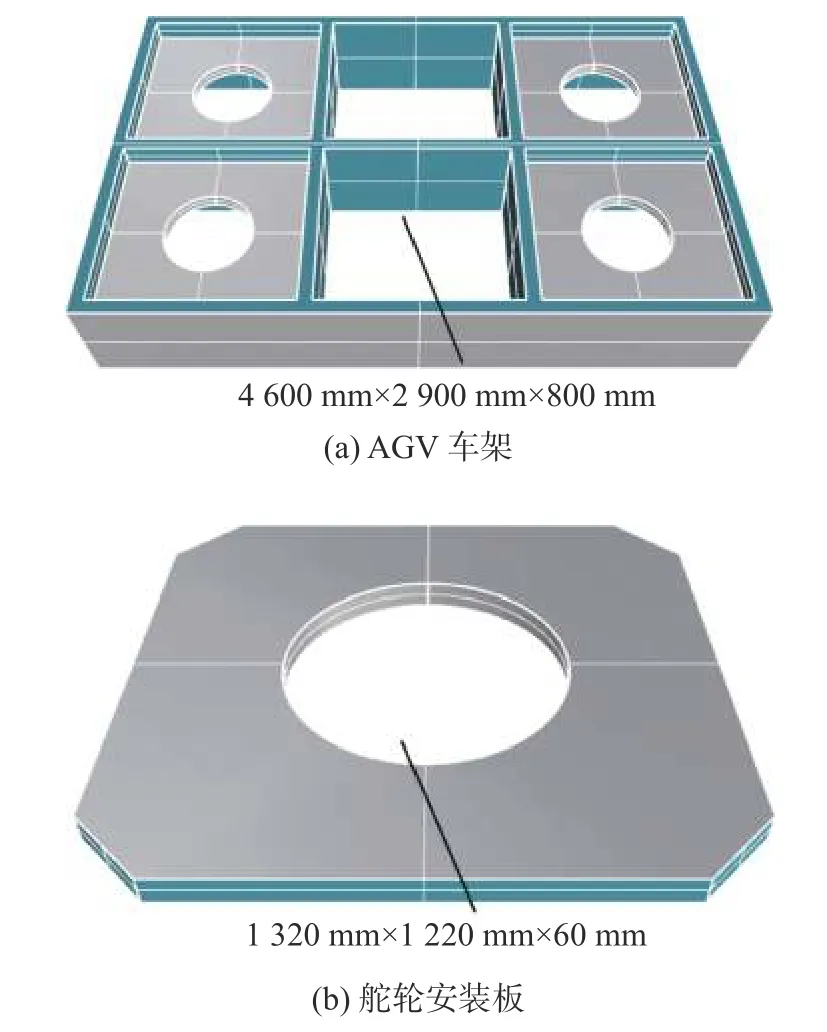
图2 承载单元初始结构Fig.2 Initial structures of bearing unit

2 理论方法

基于BESO法的拓扑优化是以结构柔顺度为目标函数，单元密度为设计参数，平衡方程为约束条件的拓扑优化模型。在该方法中，首先，去除部分结构相关性小的特征如倒角、细小孔等，在简化基础几何模型的基础上划分网格；然后，根据装配需求设定设计区域与非设计区域，根据核定工况设定相应载荷及约束条件；接下来，进一步设定进化率、材料删除率、材料增加率，计算单元灵敏度，逐步删除低效单元并在高效单元附近生成新单元，使结构趋于平衡，达到目标体积并且收敛。基于BESO法的拓扑优化计算流程如图3所示。

图3 基于双向渐进结构法的拓扑优化计算流程Fig.3 Topology optimization calculation process based on the BESO method

2.1 拓扑优化模型及刚度灵敏度

基于连续体的拓扑优化可以描述为寻找材料在给定条件下的最佳空间分布过程，可表达为：在某种约束条件下，使得目标函数最大（小）化[21]。以结构柔顺度为目标的拓扑优化的含义可进一步解释为：在给定体积的材料下使得车身结构的平均应变能最小。该含义的数学语言为：

式中：x为单元密度矩阵；C为结构平均柔顺度；xn为n处的单元密度；Vi为i处的单元体积；Ω为设计域；U为位移矩阵；K为总刚度矩阵；V*为预设待优化体积；N为单元数量；i为单元位置；xi为i处的单元密度，是设计变量，有且只有两种取值（1或为一个接近0的数xmin，如0.001），分别对应计算过程中某单元保留或删除的状态。对结构整体的刚度平衡方程为：

式中，ui为删除第i个单元后该节点处的位移矩阵，ki为第i个单元的刚度矩阵。对目标函数求导可得：

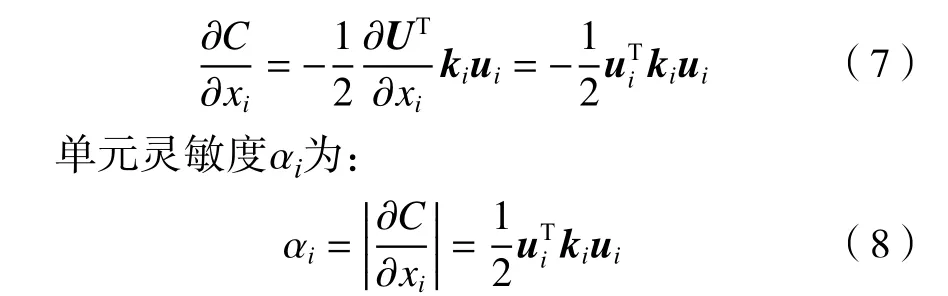
由式（8）可以看出，单元灵敏度αi在数值上等于删去i单元对计算域中任一单元处产生位移的贡献，若载荷施加于此处，则αi表示i单元的应变能。定义αdel为灵敏度删除阈值，若αi小于αdel，则删除i单元；定义αadd为灵敏度增加阈值，若αi大于αadd，则生成i单元[22]。反复进行单元灵敏度计算并增删单元，直至：

式中：m、k为当前迭代步数，为正整数；ε为收敛控制因子。当最近5次的结构柔顺度的相对变化值小于控制因子则判断迭代收敛。

2.2 过滤半径

BESO方法中单元密度有两种取值（即1和接近0的小数），对应两种存在状态。这就导致进行拓扑优化计算时，在某些区域可能形成过于细小的分叉结构，分叉形貌的出现不利于拓扑结构的实际生产加工。为此，应用单元格灵敏度过滤技术解决这一问题。首先，设置过滤半径，值为网格尺寸的整数倍，然后计算过滤半径范围内所有单元的灵敏度加权平均值之和作为该单元的灵敏度，如式（10）、（11）所示。

图4为不同过滤半径下的拓扑结构，其中，3*和4*分别为3倍、4倍网格尺寸。通过对单元灵敏度的重新加权计算，消除了体积过小的材料空缺部分，重新计算的结构更加适合应用到实际生产加工。

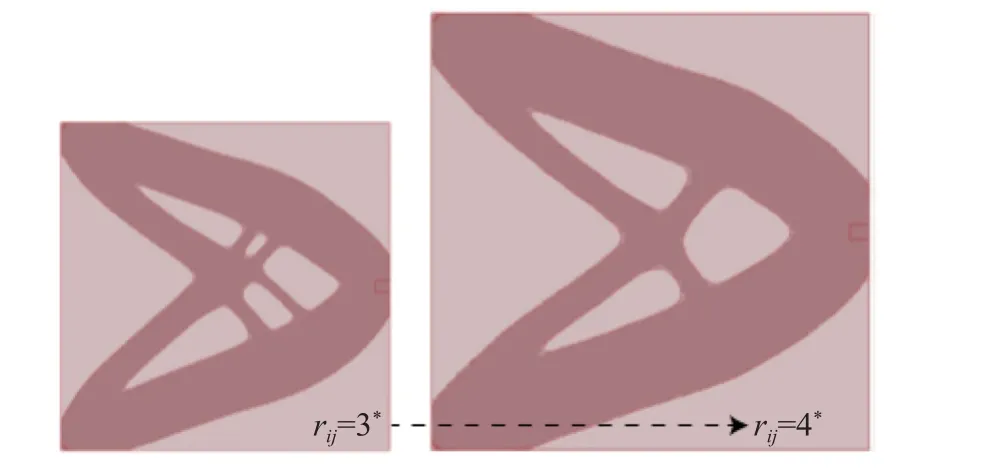
图4 过滤半径为3倍、4倍网格尺寸下拓扑结构Fig.4 Topological structures under filter radius of 3 and 4 times mesh size

2.3 方法验证

MBB梁是Messerschmitt-Bölkow-Blohm公司生产的一种飞机支撑梁结构，常用作验证拓扑优化的基准算例。使用固体各向同性材料惩罚（SIMP）模型对长6 m、宽1 m，材料为结构钢的初始设计区域进行拓扑优化计算。初始结构两侧为辊支撑，受力点位于上方边缘中心处，总力F为100 kN，方向垂直向下。结构钢密度ρ为7 850 kg/m3，弹性模量E为200 GPa，泊松比ν为0.3，网格尺寸为6 mm，体积约束V*为0.5。总体结构及受力情况如图5所示。

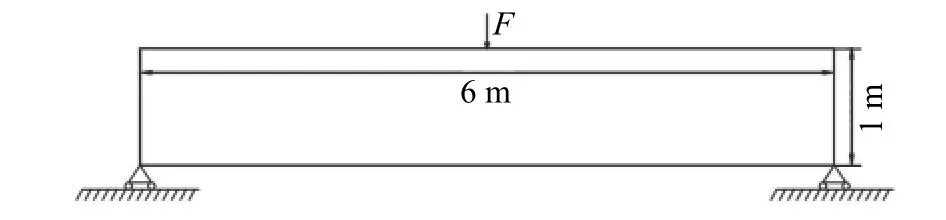
图5 MBB梁结构示意图Fig.5 Schematic diagram of MBB beam

BESO方法与SIMP方法对MBB梁的拓扑优化结果比较如图6所示，BESO方法拓扑优化后的结构形状、截面尺寸与基准算例的一致性良好。

图6 MBB梁拓扑优化结果Fig.6 Topology optimization results of MBB beam

3 重载AGV承载部件优化

3.1 CFRP力学性能实验

CFRP具有各向异性和不均质性[23]，且不同的成型工艺对材料性能影响较大。本文选用T300碳纤维布为增强材料，GE-7118A环氧树脂为基体材料，基体树脂具有粘接牢固、交联密致、工艺成熟的特点[24]。以VARTM工艺制备尺寸分别为250 mm×50 mm和50 mm×20 mm的复合材料矩形试样。

根据标准GB/T 1447-2005[25]及ASTM D3518/D3518-M13[26]进行0°和90°拉伸实验及面内剪切实验，采用应变片和移动应变仪对实验过程中的应变进行测量，均在低应变速率电子万能材料实验机上进行，实验速率为2 mm/min。首先，制备层数为3、4、5、6、8层的5组不同厚度0°铺层平纹层合板，比较不同层数下CFRP的力学性能；其次，在相同厚度下，制备层数为6层的0°、90°铺层平纹和单向层合板，比较不同编织方向对CFRP力学性能的影响。每组实验分别进行5次，整理实验数据，获得的CFRP力学性能参数见表1。

表1 CFRP力学性能参数计算结果Tab.1 Calculation results of mechanical properties of CFRP

3.2 拓扑优化结果

初始设计域根据实际生产的车架设置尺寸为4 600 mm×2 900 mm×800 mm的长方体，各板件厚度均为100 mm，开孔直径640 mm，材料为结构钢，四面体网格边长尺寸为16 mm，体积约束V* 为 0.5。开孔处设置3轴位移约束为0，受力面为车架上表面，以法向核载8×105N匀布于面积为2.42×106mm2的受力面上，进化率和删除率为2%，车架的拓扑过程如图7所示。

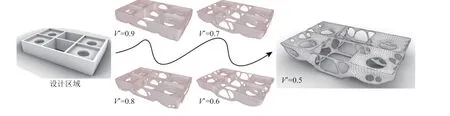
图7 重载AGV车架拓扑优化结果Fig.7 Topology optimization results of the heavy-duty AGV frame

舵轮安装板的拓扑优化初始设计域为1 320 mm×1 220 mm×64 mm的长方体，四周倒角长度为150 mm，中心开孔直径为640 mm，由于车体由4舵轮组驱动，单个舵轮安装板所受载荷为2×105N，匀布于大小为1.29×105mm2的受力面上，四周倒角处约束3轴方向位移为0。材料为CFRP，四面体网格边长尺寸为8 mm，体积约束V*为0.5，优化求解过程如图8所示。

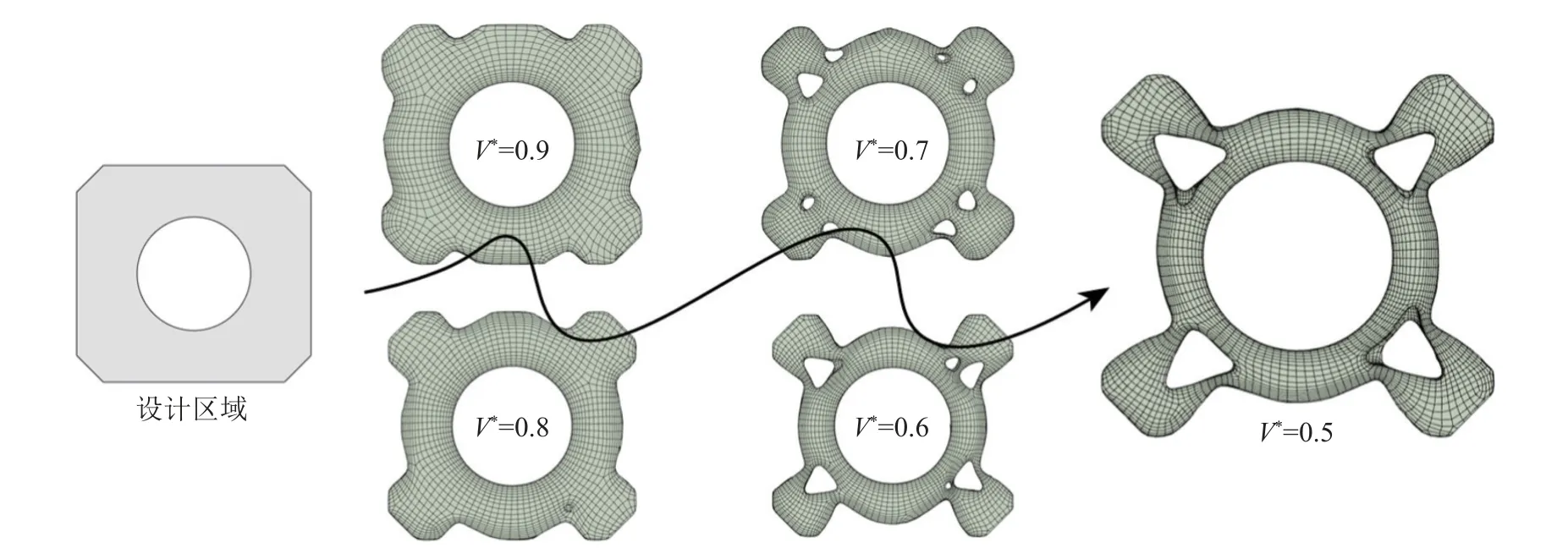
图8 舵轮安装板拓扑优化结果Fig.8 Topology optimization results of the steering wheel mounting plate

图9为拓扑优化后的重载AGV车身总成，根据车架及舵轮安装板的拓扑优化结果，综合考虑实际生产成本及工艺性，确定设计方案如下：车身整体尺寸为4 600 mm×2 900 mm×800 mm维持不变，车架上表面梁截面尺寸为100 mm×100 mm矩形，下端梁截面尺寸为150 mm×100 mm矩形。车首尾呈弧形，中部呈M型支撑结构。安装板与车身之间及舵轮组之间均由螺纹连接。

图9 重载AGV车身总成设计方案Fig.9 Design scheme of heavy-duty AGV body assembly

3.3 CFRP铺层优化

由于碳纤维复合材料显著的各向异性，碳纤维的铺层与结构强度密切相关，为了发挥碳纤维在主方向上高模量、高强度的特点，因此对铺层角度进行优化设计。图10为4层初始角度为[0/45/90/-45]、单层厚度为0.3 mm的典型铺层结构。在软件COMSOL Multiphysics 5.6中使用第3.1节计算得到的CFRP力学性能参数，依照核定工况的受力方向及约束位置施加载荷及约束，目标函数为面内最大Mises应力，进行铺层角度优化计算。

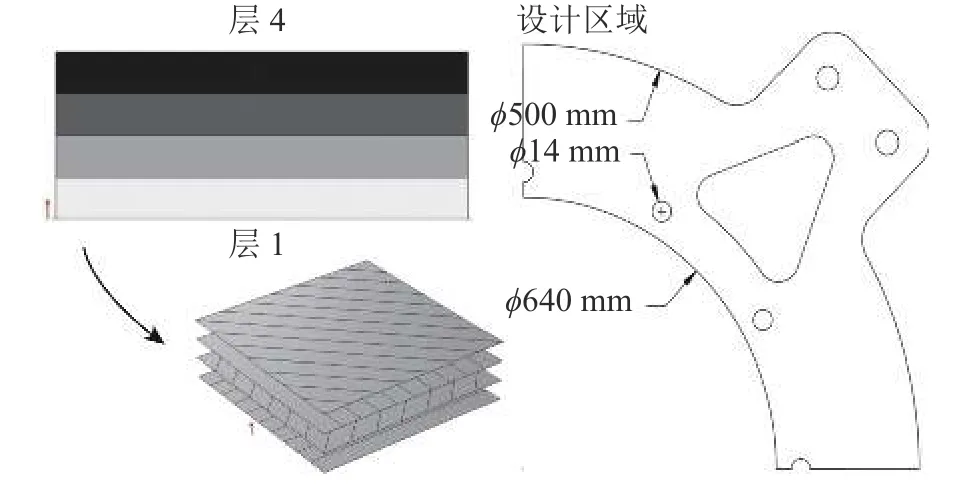
图10 铺层优化几何示意图Fig.10 Geometry schematic of stacking sequence optimization

铺层优化前后角度对比见表2。CFRP铺层角度如图11所示。

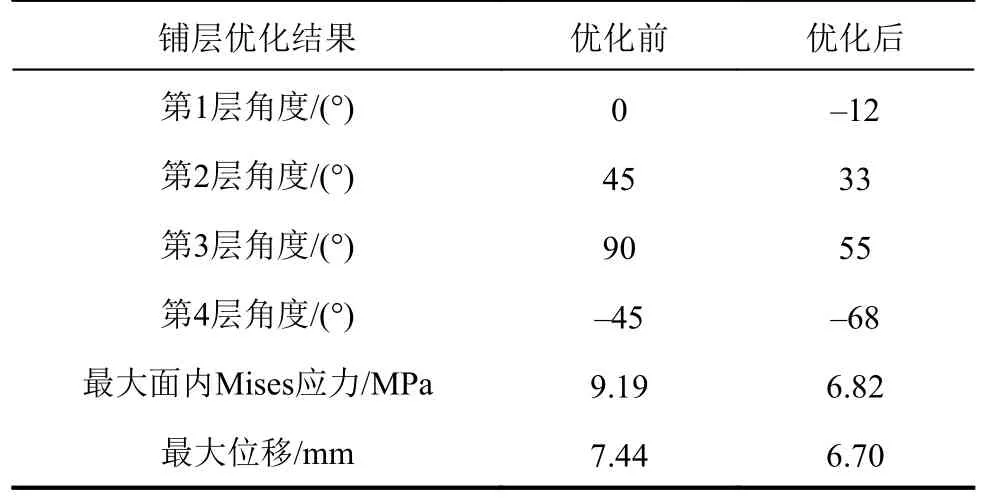
表2 CFRP铺层角度变化Tab.2 Variation of CFRP stacking angle

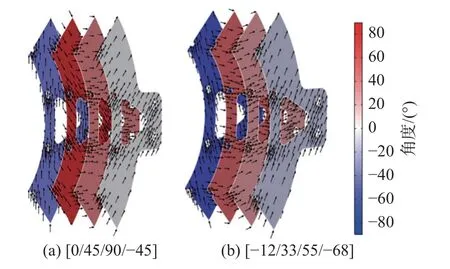
图11 CFRP铺层角度Fig.11 Stacking angle of CFRP

由表2可知，铺层方向调整后，多层材料的面内最大Mises应力降低了25.79%，最大位移降低了9.95%。

3.4 静应力分析及模态分析

重载AGV在设计及实际使用时对在复杂空间内的对接精准度和在运载大型货物时平稳性要求较高，因此，可以将负载移动过程看作为准静态过程，此外，需考虑重载AGV在行进过程中路面状况对于车身结构稳定性的影响。基于此，在软件COMSOL Multiphysics 5.6中对处于核定工况下（即承载面受法向8×105N匀布载荷）的车身总成分别进行静应力分析及模态分析。

将车身总成进行对称简化，单个承载单元由1/4车架与1个完整舵轮安装板构成，车架与舵轮安装板之间由螺纹连接。所有螺纹连接处设置为弹簧基础，弹簧类型选择单位面积的弹簧常数KA= 107N/m3，内圈螺纹面设置为非行进方向无位移。车架上表面为受力面，受法向载荷2×105N，并全域受自重载荷；材料方面，车架为结构钢，舵轮安装板为CFRP，单层厚度为0.3 mm，将第3.3节中优化铺层角度后的4层作为一组并重复50次，总层数为200层。设置网格变化率为1.2，有限元计算结果如图12所示。

图12 重载AGV车身总成有限元计算结果Fig.12 Finite element analysis results of heavy-duty AGV body

图12中，Mises应力由等值线表示，内圈螺纹处应力较大，最大值为8.42×107N/m2。舵轮安装板处应力梯度较大，越远离螺纹连接处则应力梯度越小。总位移由云图表示，集中于车架外缘及中段部分，最大位移位于车架外侧上表面处，大小为0.09 mm。单个舵轮安装板的重量从628.12 kg下降为55.44 kg，降低了91.17%，整个车身装配体的重量由15 914.97 kg下降为12 447.59 kg，降低了21.79%。在空载的情况下，优化前后车身总成的静力分析及模态分析结果见表3。

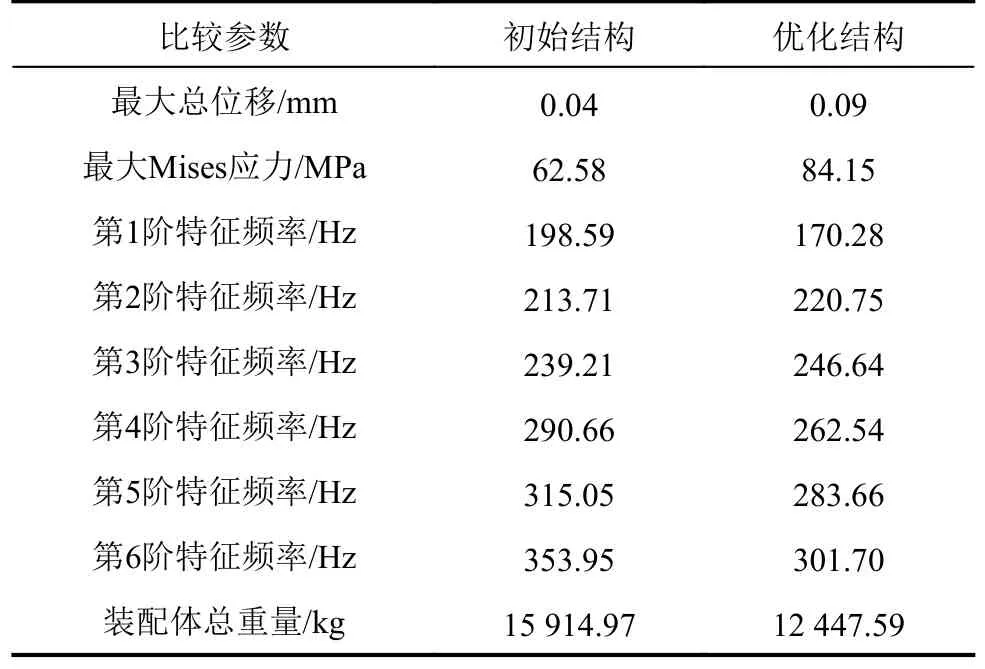
表3 初始与优化结构静力分析及模态分析结果Tab.3 Results of static analysis and modal analysis of the initial and optimized structure

由表3可知，在空载时，优化前后结构的前6阶特征频率均呈稳定上升的态势，初始结构的特征频率比优化结构的略高，优化结构的特征频率变化更加平缓。重载AGV在运行过程中的车辆振动主要受路面起伏及外加载荷影响。由于重载AGV的车速及对行驶路面的要求均有规范，路面的振动激励一般在20 Hz以下，与该车身总成的前6阶特征频率均无交叉，因此该AGV在行进过程中能够有效避免共振的出现。

由于外加载荷对重载AGV特征频率影响较大，因此，在单个承载单元上计算不同载荷下的特征频率。优化结构的特征频率随受力面法向载荷变化情况如图13所示，在核定工况范围以内，车身总成的特征频率随着载荷增加而呈减速下降趋势。在空载时前6阶特征频率均为最高，各阶特征频率之间差距随着法向载荷的增大而减小。第1阶特征频率下降幅度最小为62.62%，在满载情况下，车身的特征频率最小为61.95 Hz，因此正常工作状态下装卸货物不会引起共振。车身在各阶特征频率下的振型如图14所示。

图13 特征频率随受力面法向载荷变化规律Fig.13 Variation of eigenfrequencies with normal loads of bearing surfaces

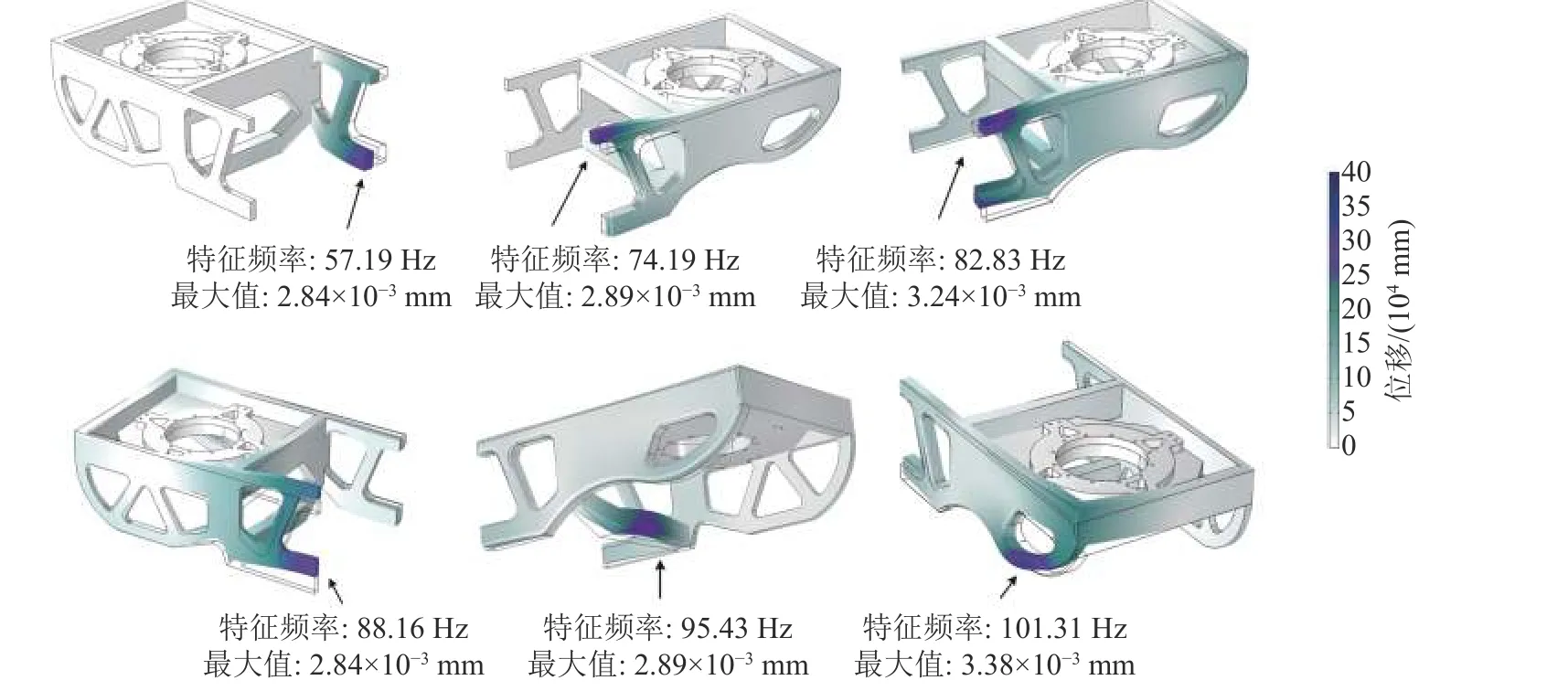
图14 重载AGV车身总成振型Fig.14 Mode shape of the heavy-duty AGV body

由图14可知，车身整体变形幅度较小。车架中部梁相较于其余部分更容易发生小幅弯曲及扭转，其中车架外侧的中部梁及车头外侧部分形变幅度较大，达到3×10-3mm。重载AGV在受激励时，振动引发的形变由车架中部逐渐传播至车架首尾处。

4 结 论

1）针对80 t级重载AGV的轻量化生产需求，对主要承载结构进行总成优化设计。基于BESO方法对车架及舵轮安装板分别进行拓扑优化；采用CFRP作为舵轮安装板材料，使新车身总成在不大幅增加最大应力及位移的前提下重量降低21.79%，其中，舵轮安装板的重量仅为初始结构的8.83%。

2）通过VARTM法制备了CFRP试样，并经过拉伸及面内剪切实验计算出力学性能参数，同时通过铺层角度优化确定了该材料应用于舵轮安装板时的较优铺层方向为[-12/33/55/-68]。有限元分析表明：核定工况下最大应力位于舵轮安装板与车架内圈螺纹连接处，大小为8.42×107N/m2；最大位移位于车架外侧上表面处，大小为0.09 mm，符合强度要求。

3）模态分析表明：新车身的特征频率在核定工况范围内随着载荷增加呈减速下降趋势；满载情况下，特征频率在61.95 ～ 109.75 Hz之间变化平稳，显著高于路面激励，可以有效避免共振的发生，受激励时形变幅度整体较小，具有良好抗振性能。