椭球颗粒体系宏、细观特性的3维离散元分析

肖浩波，漆天奇，杨舒涵,2，周 伟，刘嘉英

(1.长江勘测规划设计研究有限责任公司，湖北 武汉 430072；2.流域水安全保障湖北省重点实验室，湖北 武汉 430072；3.武汉大学 水资源与水电工程科学国家重点实验室，湖北 武汉 430072；4.浙大城市学院 土木工程系，浙江 杭州 310015；5.城市基础设施智能化浙江省工程研究中心，浙江 杭州 310015)

颗粒材料是地球上存在最多的材料之一，广泛存在于自然界和工业界，其大多由不规则形状的颗粒组成。以堆石料为例，由于其对地形和地质条件适应性好、可就地取材，在大型水电、港口、交通等基础设施的建设中被广泛应用。这些工程的安全运行与人民群众的生命财产安全息息相关，因此，迫切需要深入研究不同颗粒形状材料的宏、细观力学特性，提高人们对颗粒材料建设工程的多方面认识[1]。

随着微观力学的发展，研究学者发现岩土颗粒材料的宏观响应高度依赖于颗粒的堆积形态和相互作用；而颗粒的相互作用与颗粒的几何特征（如颗粒的形状和大小）密切相关，其中颗粒形状的影响更为显著[2]。诸多研究学者[3-6]强调了颗粒形状对岩土颗粒材料力学性能的重要意义。研究表明，由于颗粒形状的不规则阻碍了粒子的转动，从而增强了颗粒之间的“互锁”效应[7-8]，影响颗粒间接触力的大小分布和颗粒排列，进而影响颗粒材料的抗剪强度[7]、内摩擦角[9]、压缩性[10]和剪胀性[11]等。Cho等[2]指出与颗粒形状不规则相关的微观机制是影响颗粒材料宏观响应的主要原因，其包括：转动受阻、滑移和颗粒重排能力等。Zhao等[8]发现非球度能够增强颗粒之间的互锁能力，使颗粒集合体的滑动接触比例增大。Nguyen等[12]通过排水和不排水加载试验发现大部分的本构模型参数受颗粒形状的影响较大。

离散单元方法（discrete element method，DEM）[13]为颗粒材料颗粒尺度力学行为的研究提供了技术手段[14-17]。与此同时，颗粒材料的微观接触网络[15]、介观结构[16]、细观组构[17]等的研究为揭示颗粒材料复杂的宏细观力学特性提供了新的途径。为了兼顾计算效率，同时考虑颗粒形状的影响，一些学者采用抗转动模型，在颗粒间的接触处施加抗旋转力矩[18-19]，以此近似考虑颗粒形状的影响。还有一些学者采用颗粒簇[20]、多面体[21]、椭球[22-23]表示不规则的颗粒形状进行数值模拟研究。椭球颗粒是描述各向异性岩土颗粒材料的最简单形状，而且还可以排除棱角、表面粗糙度等的干扰。故本文采用椭球颗粒进行数值模拟试验，通过改变椭球颗粒的伸长率LAR研究颗粒形状的影响。

目前，对于颗粒形状的研究主要基于常规三轴加载试验，而其在复杂应力路径下对岩土颗粒材料的影响机制尚不明确，不同宏观抗剪强度和体积变形响应下各类细观结构的作用机制还有待进一步研究。

真三轴应力路径能够反映颗粒材料的真实状态。本文将基于真三轴离散元数值试验，分析不同椭球颗粒体系宏观力学响应，以及其接触网络的配位数分布、接触力、组构张量及各向异性等细观特征的演化，并验证常用3维强度准则对椭球颗粒体系的适用性，从细观尺度揭示颗粒形状对颗粒材料3维宏观力学行为的作用机制。

1 DEM数值试验

采用开源软件LIGGGHTS进行离散元数值模拟[24]。制样时，在0.28 m×0.28 m×0.28 m的立方体空间中生成服从正态分布的椭球颗粒，共计20 000个。椭球颗粒大小采用与颗粒等体积球体的等效半径表示，共生成4组试样，各组椭球颗粒试样的伸长率LAR分别为1.2、1.4、1.6、1.8，如图1所示。

图1 不同伸长率的椭球形状Fig.1 Ellipsoid shape with different elongation

试样生成后，采用各向同性压缩的方法固结，六面刚性墙体缓慢向中心移动直至达到目标围压0.5 MPa。固结过程中，通过调整颗粒间的滑动摩擦系数，使4组试样的初始孔隙比均约为0.345，颗粒间接触模型采用Modified Hertz-Mindlin模型[25]。加载过程中的滑动摩擦系数μ取0.5。数值模拟细观参数见表1。

表1 数值模拟细观参数Tab.1 Parameters used in the DEM simulation

加载时，试样顶部和底部的边界以合适的速度匀速移动，而四侧的边界按照伺服机制进行调整。顶部和底部边界的运动速度要足够小[8]，以保证试样为准静态加，试验中惯性指数I为3.5×10-4：

等σ3（第3主应力）、等b（中主应力比）的真三轴加载过程中，采用伺服机制控制边界条件，保持小主应力σ3不变，恒定在0.5 MPa；同时，试样的中主应力σ2控制条件为：

式中，主应力比b分别取0、0.2、0.4、0.6、0.8、1.0。其中：当b=0时，为三轴压缩路径；当b=1.0时，为三轴拉伸路径。由于制样时采用刚性边界且初始试样为正立方体，数值试样很难达到理想的临界状态。本文选取偏向应变35%时为试样的临界状态，4组试样的初始状态和临界状态如图2所示。

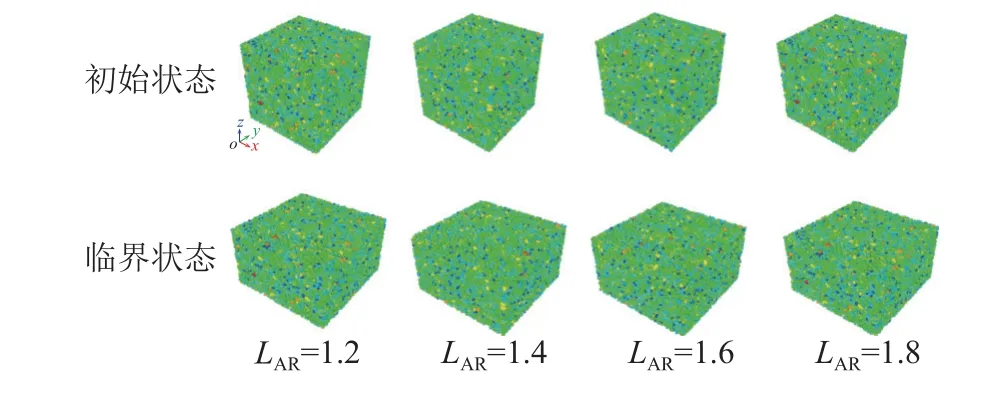
图2 椭球颗粒试样初始状态和临界状态Fig.2 Morphology of specimens with different particle shapes in initial and critical states

2 宏观力学响应

2.1 加载过程中的应力应变

椭球颗粒试样在三轴压缩路径（b=0）条件下，偏应力比q/p、体积应变εv随剪应变εd的演化曲线如图3所示。图3中，体积应变以剪缩为正，剪胀为负。由于各个试样的初始体积分数大致相同，不同椭球试样的峰值偏应力比随伸长率LAR的增大略微减小，残余应力比随LAR的增大而增大。体积响应表现为：试样均发生剪胀，随着LAR增大，试样进入剪胀的速率越快、剪胀程度越明显。

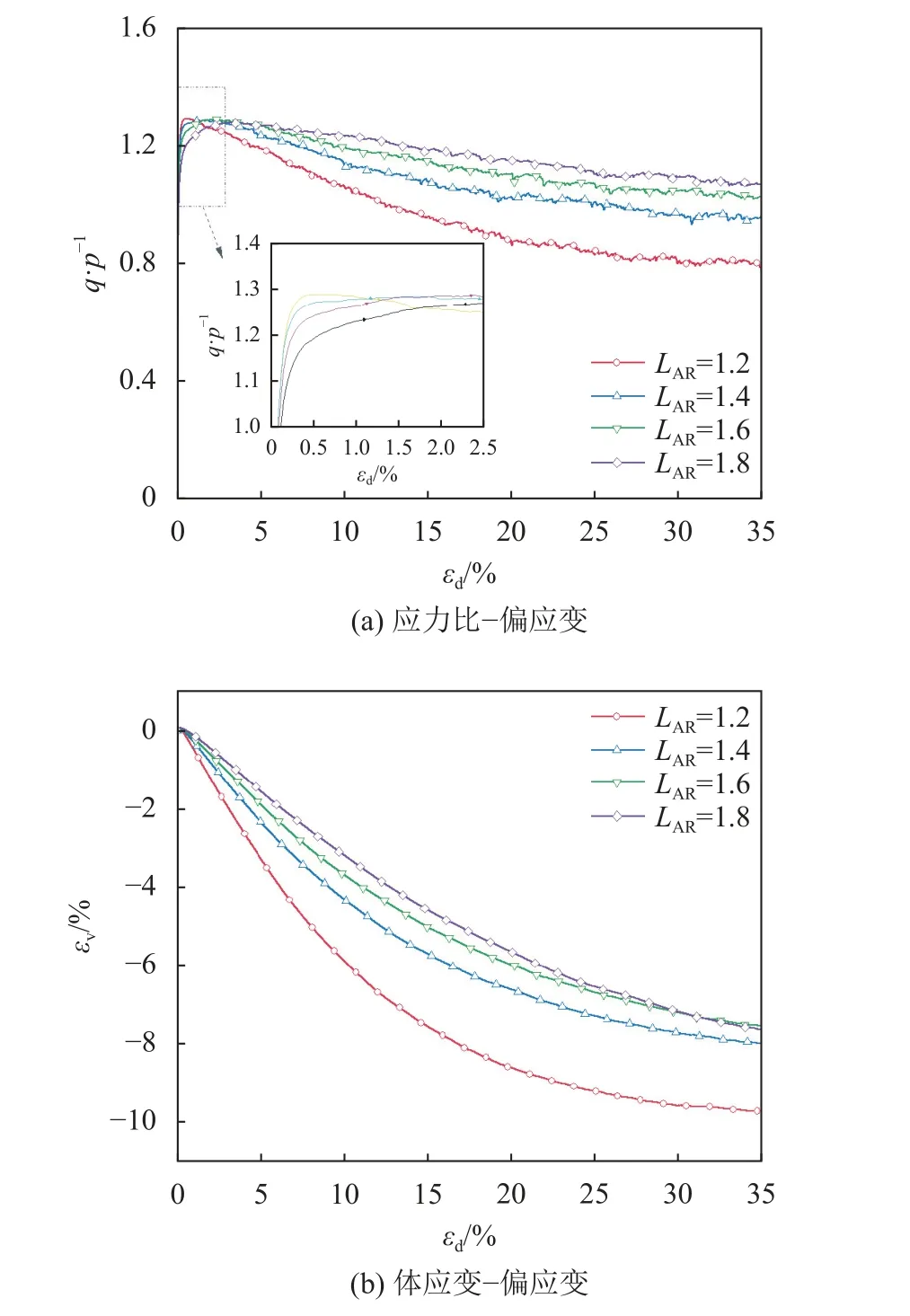
图3 不同颗粒形状试样的应力应变的演化规律 （b=0）Fig.3 Curves of stress-strain relationships for different particle shape system (b=0)

刘嘉英等[27]研究表明，在3维加载前期，圆球颗粒试样体应变εv的演化过程近似一致。图4给出在3维路径下，LAR=1.4的椭球颗粒试样体应变演化过程。由图4可见，试样初始均发生剪胀，且体应变εv在加载前期（偏应变10%以内）的演化过程近似一致，不受中主应力比b的影响。该规律对于LAR=1.2、1.8的椭球颗粒试样同样适用（由于篇幅有限未列出），说明3维路径下试样加载前期体应变演化的一致性规律不受颗粒形状的影响。

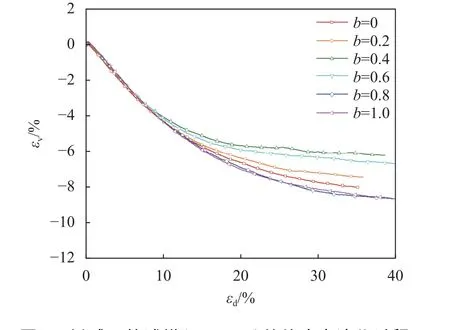
图4 椭球颗粒试样（LAR=1.4）的体应变演化过程Fig.4 Volumetric strain evolution of an ellipsoid particle sample (LAR=1.4)

2.2 3维应力面

在主应力空间中，垂直于空间对角线的偏平面为π平面，则主应力空间中任意点（σ1、σ2、σ3）投影在π平面上的矢径rσ和应力罗德角θσ分别为：

通过计算不同加载路径下峰值和临界状态应力投在π平面的极坐标rσ和θσ，绘制π平面的应力面，如图5所示。临界和峰值状态π平面的应力面类似于Lade面，呈现出正三角锥形，其3维应力特征符合真三轴试验的一般规律。椭球试样峰值状态的应力面受伸长率LAR的影响较小，主要因为各椭球试样的初始体积分数相差不大；而临界状态的应力面随LAR的增大而增大，是由于椭球颗粒伸长率的增大加强了颗粒间的咬合作用，使颗粒体系的抗剪强度增大。

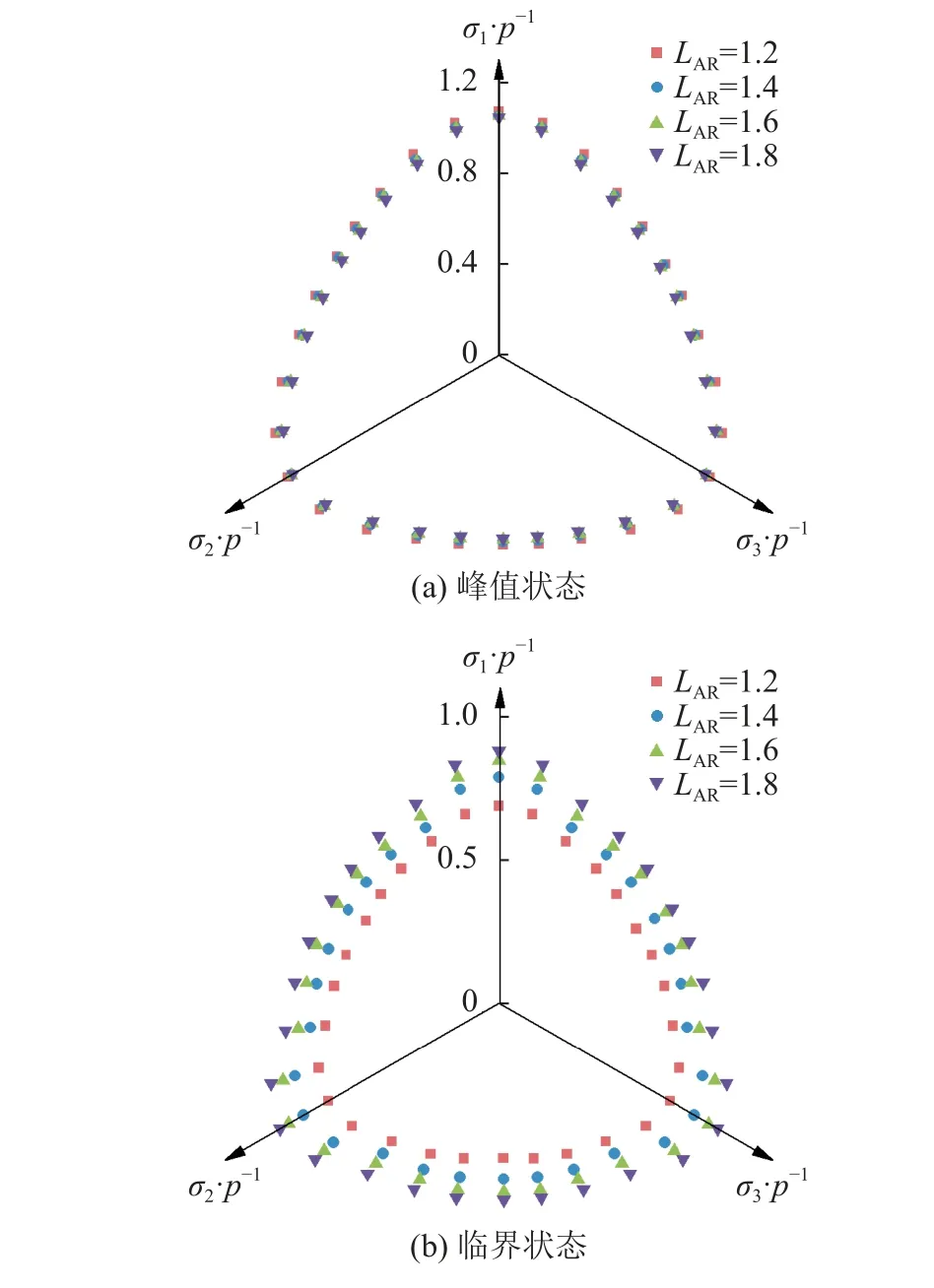
图5 不同伸长率的椭球试样在π平面的应力面Fig.5 Stress surface for samples of different LAR on πplane

2.3 3维强度准则的适用性

在等σ3及等b加载条件下，不同伸长率的椭球试样峰值内摩擦角均随中主应力比b发生变化，如图6所示。图6中，sinφ=（σ1-σ3）/（σ1+σ3）。由图6可见：在三轴压缩路径（b=0）下，各试样的峰值内摩擦角相差不大；当b≠0时，随着LAR增大，3维峰值内摩擦角增大；在3维加载条件下，随着中主应力比b的增大，各试样的峰值内摩擦角均表现出先增大后减小的现象，并在b=0.6时达到最大值；且三轴拉伸路径（b=1.0）下的峰值内摩擦角高于三轴压缩路径（b=0）下的内摩擦角。

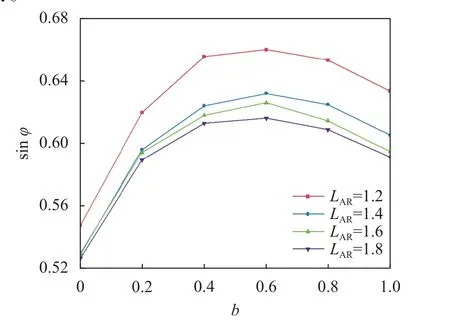
图6 椭球伸长率对3维峰值内摩擦角的影响Fig.6 Influence of aspect ratio of ellipsoid on 3D response of peak internal friction angle

常用的3维强度准则有Mohr-Coulomb、Lade-Duncan和Mastsuoka-Nakai准则，其中：Mohr-Coulomb准则认为在任意加载路径与常规三轴压缩路径的内摩擦角相等，即φb=φb=0，与模拟的结果不符（图6）；Lade-Duncan准则、Matsuoka-Nakai准则考虑了不同应力路径对峰值内摩擦角的影响。施维成等[28]对砾石料进行等σ3等b试验，建立了一个强度准则能够反映内摩擦角与b的关系。为了检验这些3维强度准则对椭球颗粒试样的适用性，图7给出了各个准则预测的φb-b关系曲线及不同椭球试样数值模拟结果的对比。

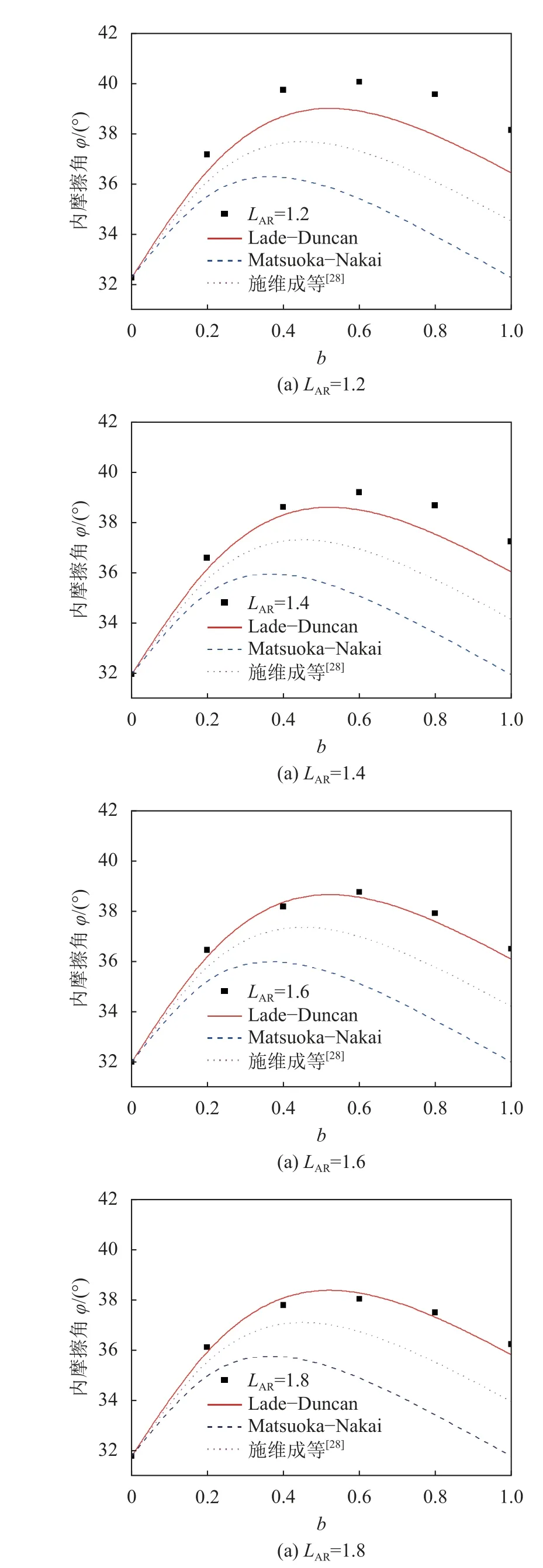
图7 不同椭球试样在3维加载条件下的φ-b关系Fig.7 φ-b relationship of different ellipsoidal specimens under true triaxial tests

定义一个误差指标δIndexe如下[29]：

由表2可知，随着LAR增大，各准则的预测误差越来越小，其中，Lade-Duncan准则的预测结果最接近模拟值，其次是施维成等[28]提出的准则和Matsuoka-Nakai准则。当LAR=1.8时，Lade-Duncan准则的预测值与模拟值高度契合，误差仅为0.77%，说明Lade-Duncan准则对级配为2～9 mm的椭球颗粒试样具有较好的适用性，且这种适用性随着形状参数LAR的增大而更强。同时，进一步说明了Lade-Duncan准则在一般岩土材料中的适用性。

表2 3维强度准则预测误差Tab.2 Prediction errors of three-dimensional strength criteria%

3 颗粒形状对细观结构的3维响应

3.1 3维组构张量与强接触网络

各向异性不仅反映了颗粒体系内颗粒、孔隙和颗粒间接触的空间排列，也反映了荷载作用下颗粒集合体微观结构的变化[30]。本文采用Oda等[31]提出的组构张量表达式，量化接触法向的方向分布：

式中：ni、nj为接触法向n在笛卡尔坐标系下的分量；Nc为颗粒体系中的接触总数； Φij=1。聚焦到一个给定的接触，接触的几何特征接触法向n、枝向量d（连接两个颗粒质心的向量）如图8所示。图8中，t为接触法向n的切向向量。

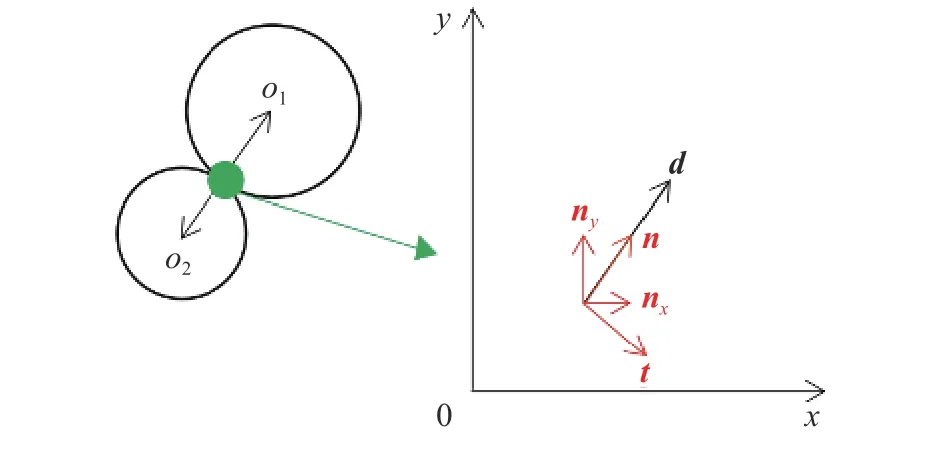
图8 接触的几何特征Fig.8 Contact geometrical characterization

在加载过程中，由于内部结构对力链的影响，接触力的分布是不均匀的。Radjai等[15]将颗粒体系的接触网络划分为两个互补的子接触网络，即强接触网络和弱接触网络。其中，强接触网络的接触传递高于均值的接触力，形成了体系内传递力的主要通道；弱接触网络的接触承载低于均值的接触力，为强接触的屈曲提供稳定。强接触网络的组构张量表示为：

椭球颗粒试样在峰值和临界状态的组构面在π平面的分布呈大小不同的“倒三角锥型”，如图9所示，与宏观π平面应力面的形状相反（图5），同Thornton等[32]发现的规律一致。

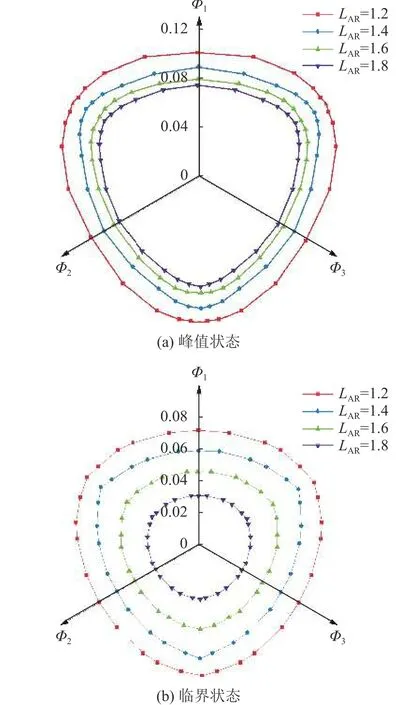
图9 π平面的组构面Fig.9 Fabric surface for samples on π-plane

由图9可见，随着LAR的增大，峰值状态和临界状态π平面的组构面均在减小，说明LAR的增大使得体系内颗粒配位数增大，组构各向异性程度减小。对比图5（b），随着LAR的增大，临界状态应力面逐渐增大，而其组构面随之减小，呈现截然不同的变化规律，说明LAR的增大使得颗粒间的咬合作用增强，增大了颗粒体系宏观的残余应力；颗粒体系细观组构变化由于受体系内颗粒排列的影响，特别是弱接触网络的影响，其各向异性程度反而减小，故在临界状态椭球颗粒试样的宏、细观响应不一致。

不同椭球试样的强接触网络在峰值状态下的三维组构面与宏观应力面的形状一致，呈大小不同的“正三角锥型”，如图10所示，与图5相一致。说明强接触网络的组构各向异性与宏观剪应力的3维演化规律一致[33]，强接触网络的组构对宏观偏应力的贡献占主导位置，这一现象与颗粒形状无关，是颗粒体系宏观应力与细观组构间普遍适用的规律。

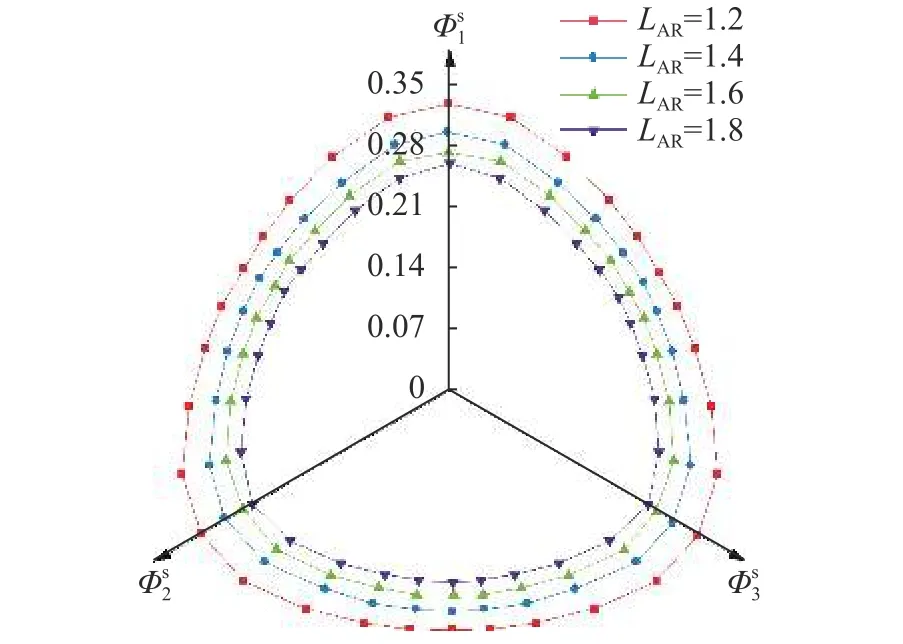
图10 强接触网络峰值状态组构面Fig.10 Fabric surface for strong contact network of sample on π-plane

由图11可见：不同b值下椭球颗粒体系q/p与ΦSd/ΦSm的比值存在线性关系，说明强接触网络对颗粒体系宏观应力的主导贡献；但其线性关系随b值而改变，说明在3维加载路径下椭球颗粒体系内的宏观应力比不能单纯由强接触网络的细观组构比推导出来，还有一部分贡献来自于弱接触网络。

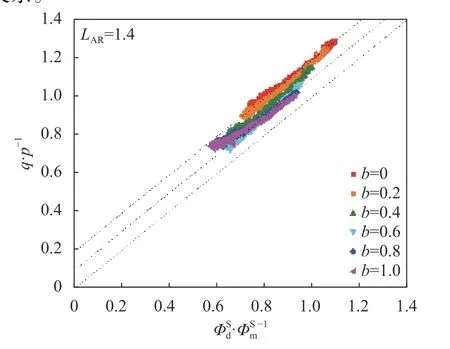
图11 3维加载路径强接触组构比与宏观应力比的关系Fig.11 Relationship between fabric ratio and macro stress ratio of strong contact under 3D loading path

3.2 细观接触的连通性

总接触网络及强接触网络在不同加载状态下的配位数分布如图12所示。图12中，横坐标为单个颗粒的配位数个数，纵坐标为具有同样配位数颗粒在体系内的个数。Liu等[17]认为配位数越少的颗粒所受约束较少，各向异性程度相对较高。由于各试样初始密度相同，故在初始状态总接触网络具有相同的配位数分布。随着外荷载的施加，体系内的颗粒发生重排，LAR越大的颗粒试样越密实，有效配位数越大，具体表现为随着LAR的增大，颗粒体系中配位数大于5的颗粒个数增多，小于5的颗粒个数减少。值得注意的是，峰值状态不同椭球颗粒体系的强接触网络的配位数分布是一致的，不随LAR变化，或许因为此时强接触网络的配位数分布为最优状态，这种最优的配位数分布与颗粒形状无关。

图12 不同接触网络中配位数的分布Fig.12 Distribution of coordination number in different contact networks

颗粒体系的宏观承载能力与细观尺度上颗粒的接触状态和接触分布密切相关。邹宇雄[35]、刘嘉英[27]等认为颗粒体系内部法向接触力的概率分布与颗粒形状和加载路径无关，本文的验证认为，当一个颗粒体系受到外部荷载时，其法向接触力的分布概率是保持不变的，颗粒体系宏观抗剪强度的改变在于颗粒体系内法向接触力大小及各向异性程度。

图13给出了LAR=1.4椭球试样总接触网络、强接触网络的峰值配位数分布情况。由图13可见：从初始加载到峰值状态，配位数的众数发生左移，说明在受外荷载作用后试样内部颗粒重排，体系平均配位数减少；在3维加载路径中，椭球试样的总接触网络、强接触网络的峰值状态配位数分布不随加载路径（b值）改变，均表现出与中主应力比b值无关的特性。

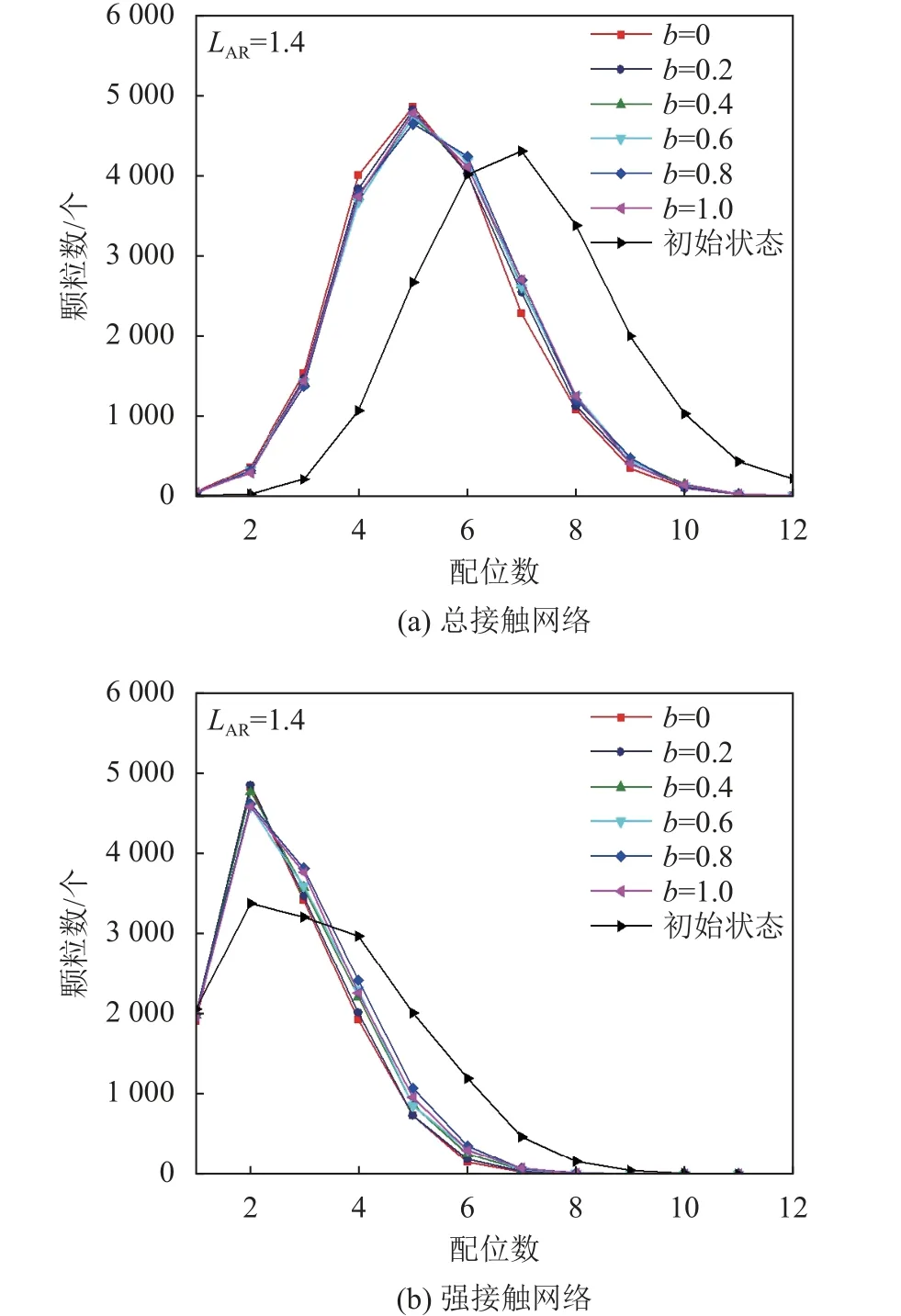
图13 峰值状态不同接触网络的配位数分布Fig.13 Coordination number distribution of different

4 结 论

本文采用离散单元法在等σ3等b的真三轴加载条件下，研究了椭球颗粒体系的3维宏、细观特性，验证了常用3维强度准则对椭球颗粒体系的适用性，阐明了椭球颗粒体系宏、细观标量在3维加载路径下的适用性。主要结论如下：

1）在真三轴加载条件下，随着LAR的增大，椭球颗粒体系的宏观应力面与细观组构面表现出不一致的演化规律。

2）对比4种3维强度准则对不同椭球试样φpeak-b关系的预测能力，Lade-Duncan准则对颗粒粒径级配为2～9 mm的椭球颗粒体系表现出较好的预测能力，且伸长率LAR越大，Lade-Duncan准则的预测准确度越高。

3）椭球颗粒体系宏观应力比q/p与强接触网络的组构偏值/均值（ ΦSd/ΦSm）之间依然存在线性关系，但线性不为1，可能归因于非圆颗粒体系中弱接触网络对宏观应力的贡献。

4）在3维应力路径下，宏观体应变在加载前期表现出与加载路径无关的性质，接触力分布、接触数目及配位数分布等细观指标表现出3维加载路径下的适用性。