基于深度教学构建高中数学深度备课模式的实践——以立体几何中的探索问题为例

文/广州市第一中学 卢 光

一、提出问题

1.从深度教学需求的角度

要达到深度教学，必须进行深度备课，这样才可以发展高阶思维能力为目标。因此，深度备课一定要思考如何让学生围绕具有挑战性的数学问题深度探究，全身心参与数学课堂的学习活动，形成积极的情感、态度，获得核心素养发展的有意义学习过程.在教师的备课中，一定要设计有理解性的、探究性的、反思性的、体验性的有意义的数学学习活动。这些都需要进行深度备课，那如何建构促进深度教学的深度备课的实施路径呢？

2.从数学课堂生成的角度

在数学课堂中，学生会提出两方面的问题，一是数学知识和数学结构的关系问题；二是数学方法和数学经验的积累问题。此时课堂中就会充满很多不同的生成性教学情境，因此我们在上课时就要进行深度备课，尽可能思考学生提出的问题，以构建：

（1）深度理解的课堂

（2）深度探究的课堂

（3）深度思维的课堂

（4）深度体验的课堂

综上所述，我尝试从五个角度实践我们建构的深度备课模式

二、 深度备课模式的构建与实施路径

1.指向思维的备课实践

备教学目标、素养目标、知识结构和知识间的逻辑关系

1.1 教学目标。（1）立体几何探索性问题的基本方法；（2）建构解决立体几何探索性问题的模型；（3）精准直观、精准方向、精准计算、精准表达。

1.2 素养培养。（1）核心素养：本题考查线面的位置关系及面面角，考查学生转化与化归的思想，考查的核心素养是逻辑推理、直观想象、数学运算；（2）解题技巧：①写全得分步骤：对于解题过程中得分点的步骤，有则给分，无则没分，所以对于得分点步骤一定要写，如在证明平行时写BG？平面ABE，CM？平面ABE；②写明得分关键：对于解题过程中的关键点，有则给分，无则没分，所以在解答时一定要写清得分关键点，如空间直角坐标系的建立时要有两两垂直的说明等；③思维发散：如何正确选择解题方法、方向。

1.3 知识结构和知识间的逻辑关系

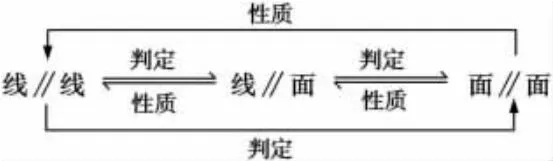
基本模型（展示熟悉、回忆加深、敏感度培养）：“线线平行”“线面平行”“面面平行”的相互转化.

2.指向理解的备课实践。（备适合学生进入深度学习的语言表达）

基本经验（提问、追问、整体问、加深对模型应用的敏感度，由点带面进行学习数学氛围养成，主要处理构造方向过程）

经验一：通过线线平行得线面平行；经验二：通过面面平行得线面平行；经验三：通过建系运算得线面平行。

如图，在三棱锥P -ABC中，PA ⊥底面ABC，∠BAC ＝90°.点D，E，N分别为棱PA，PC，BC 的中点，M 是线段AD 的中点，PA＝AC＝4，AB＝2.

求证：MN∥平面BDE.

[证明]解法一：连PN 交BE于H，连HD.

∵E、N 分别为PC、BC 的中点，∴H 为△PBC 的重心，

又DH⊂平面BDE，MN ⊄平面BDE，∴MN∥平面BDE.

解法二：取EC 的中点H，连MH、NH，

∵N 为BC的中点，∴NH∥BE.

又NH ⊄平 面 BDE，BE⊂平面BDE，∴NH∥平面BDE.

又MH⊄平面BDE，DE⊂平面BDE，∴MH∥平面BDE.又MH∩NH ＝H，∴平面MNH ∥平面BDE，∴MN∥平面BDE.

不妨设z＝1，可得n＝（1,0,1）.

3.指向深度的备课实践。 （根据学情备课堂的教学组织方式）

3.1 学情分析。（1）高二已学习过所有的概念知识，做过作业，考试后对问题解决的经验有一定的积累；

（2）高三17 班的学生整体对数学的活跃度不高，表达及回答问题的意愿不强；（3）问题是：审题方向寻找略为困难，数学问题的转化需要提升，表达的精准不够，需要教师更多通过引导学生用精确、量化、符号化的数学语言表示直观“形”的发现和转化。

3.2 教学组织方式。采用观察、归纳、启发相结合的教学方法，在学法上更多的是通过提问、相互交流进行反思沉淀，运用现代化多媒体教学手段进行教学活动。

3.3 教学内容组织。探索性问题（根据以上教学，学生实践使用基本模型和基本经验）

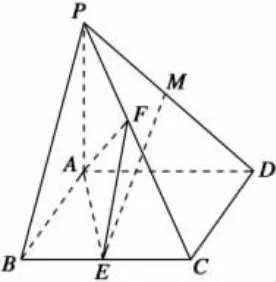
如图，在四棱锥C-ABED 中，四边形 ABED 是正方形，点G，F 分别是线段EC，BD 的中点.

（1）求证：GF∥平面ABC；

（2）线段BC 上是否存在一点H，使得平面GFH∥平面ACD？若存在，请找出点H 并证明；若不存在，请说明理由.

[解析]（1）略

（2） 当H 为BC 的中点时，平面GFH∥平面ACD.

证明如下：∵G、H 分别为EC、BC 的中点，∴GH∥BE，又BE∥AD，∴GH∥AD，

又GH ⊄平面ACD，AD⊂平面ACD，∴GH∥平面ACD.

又GF∥AC，GF⊄平面ACD，AC⊂平面ACD，∴GF∥平面ACD，

又GF ∩GH ＝G，GF ⊂平面GFH，GH ⊂平面GFH，∴平面GFH∥平面ACD.

[引申]ED 上是否存在一点Q，使平面GFQ∥平面ACD.

[解析]当Q 为ED 的中点时，平面GFQ∥平面ACD.

探索性方法（面对上题的探索，教师总结出方法，强化模型重新再建构）（1）对命题条件的探索常采用以下三种方法：①先猜后证，即先观察与尝试给出条件再证明；②先通过命题成立的必要条件探索出命题成立的条件，再证明其充分性；③把几何问题转化为代数问题，探索命题成立的条件.（2）对命题结论的探索常采用以下方法：首先假设结论存在，然后在这个假设下进行推理论证，如果通过推理得到了合乎情理的结论，就肯定假设，如果得到了矛盾的结论，就否定假设.

4.指向反思的备课实践。 （根据学情与本节课内容备课堂练习和课后作业）

4.1 课堂练习。再探索（学生自主学习，教师巡视课堂，再统一讲解问题所在）

5.指向过程的备课实践

根据学情预测学生会出现的问题，主要是6 个角度：角度一：知识结构的问题；角度二：知识间逻辑关系的问题；角度三：算法中体现的思维问题；角度四：问题情境体现的素养问题；角度五：教师课堂表达出现的理解问题；角度六：作业解决过程中出现的情感问题。

三、深度备课模式的问题审视

在实践的过程中，当形成深度备课与上课深度的良性循环后，我们还需要特别注意：如何把深度备课的过程更科学、更有生命力。因此我们更需要关注以下三点，并积极进行完善：1.教案学案设计规范的落实；2.深度备课模式实践效率的保障；3.深度备课评价指标的设计。

四、深度备课模式的反思与展望

为提升学生数学核心素养提供适合的深度教学的课堂模式，通过本人在学校的实践，特别反思两点：1.教师备课时如何在数学课堂实施深度教学的操作；2. 教师备课时如何实现在数学课堂中深度教学的注意点和关注点。