间隙对圆柱凸轮传动平稳性影响的研究

董明望 李倪明 黄 海

武汉理工大学物流工程学院 武汉 430063

0 引言

随着科学技术的飞速发展，机械工业也发生着日新月异的变化，机器性能的提升和制造标准的提高，高负荷、高强度、长时间的工作下，又往往在精度的限制下，必须保证整体部件的运动轨迹和受载强度[1]。圆柱凸轮连续传动机构在运行的过程中，凸轮槽和从动转盘上滚子的变形对总体的承载能力和受力分布以及可靠性影响较大[2]，同时也引发了有害振动隐患甚至卡死，从而造成巨大的损失；环境因素决定了内部零件应力和应变的特征，在考虑精确性下，通过仿真模拟必须考虑局部柔性零部件对于系统受力和运动的影响，在实际的设计过程中这些又是提升产品性能突破瓶颈的关键问题[3]。

传统的静态化设计手段已经不能逐渐适应现代工业和生活产品的性能要求，在日常生活使用和工程施工中，由于环境因素的差异，对圆柱凸轮机构的影响也存在着悬殊的差异。随着机械向高速化方向发展，惯性力增加，而且机构的弹性变形也给机械运动的输出带来了一些误差，对于向圆柱凸轮连续传动机构这类高精度机械，这种弹性变形不仅对于精度的影响是巨大的，甚至破坏机构的运行状态，动态化的设计显得十分必要。对此，参考一些研究案例如：王蕾等[4]利用ADAMS 软件对圆柱分度凸轮机构的运动学、动力学进行了全面的仿真分析研究，同时考虑机构实际装配制造误差分析了传动副间隙对动态响应特性的影响情况；刘海生等[5]研究凸轮与滚子之间的间隙以及输入输出轴的柔性对圆柱分度凸轮机构的动态性能影响，结论显示柔性轴会引起分度转盘的转速波动，间隙的存在和输入轴转速的提高会使分度转盘的瞬时角加速度和滚子与凸轮间的接触力成倍增加。国内外学者在研究空间凸轮的动力学特性时，将研究的重点放在了分度凸轮和空间弧度凸轮上，在做了大量的假设和简化下，鉴于动力学理论来分析机构的动力特性，依托于仿真软件ADAMS 建立三维空间模型的虚拟样机进行仿真研究验证并得出结论，得出了一组机构受间隙、结构参数、施工条件等因素的相关性案例。

此外，任何机器在运动时，运动零部件之间势必会发生摩擦和磨损，而润滑是一种有效的解决手法，张翠凤[6]指出圆柱凸轮该机构运转的可靠性取决于其圆柱凸轮与从动滚子间的摩擦学特性，2 表面间的磨损与2 表面间的接触应力、滑动速度、表面材料及润滑油有关，在工况条件和材料已给定的情况下，润滑的作用性变得尤为重要。现代润滑理论已要求在分析中把发热和传热、零部件的变形、润滑剂的流变性、工件表面的粗糙度等很多因索都考虑进去，对润滑的求解也必须仰仗计算机仿真技术和算力[7]。

本文为了提升圆柱凸轮传动机构的传动平稳性，考虑了滚子的弹性变形和润滑油膜的缓冲作用，提出了一种耦合微变形和润滑油膜的关于圆柱凸轮廓面的最优间隙值的计算方法。

1 数值模型的建立

1.1 圆柱凸轮传动机构的空间模型

本文所建立的圆柱凸轮三维模型具体数值如下：机构的传动比i= 20、基距A=100 mm、中心距C=175 mm、滚子半径r=16 mm、滚子长度H=20 mm，从动盘节圆半径rp=175 mm。该机构廓面可使用空间曲面啮合原理与空间坐标变换法可得，其中滚子的圆柱面廓面处在动坐标系内的接触点坐标为

式中：φ1为从动盘所在位置角；h为啮合点于凸轮动坐标系的啮合高度，从动盘转角的取值范围为[-18°，18°]，滚子的啮合高度的取值范围为[47，67]。

之后，经过3 次空间坐标变换以求得凸轮廓面的方程

先构建关于凸轮廓面方程的点集，为了尽可能贴合曲面，故选择更密集的点，一条曲线取2 000 个特征点，一个面间隔1 mm，共计选择21 条线使用放样命令来拟合该面，得到双侧的凸轮廓面；之后补齐圆柱凸轮机构的其他特征，完成三维模型的构建；滚子与从动盘的三维建模比较简单，省略详细说明，在Solidworks 完成装配体的组装后，保存为Parasolid 格式文件，三维模型如图1 所示。

图1 圆柱凸轮的三维模型

1.2 弹流润滑模型的建立

流体动力润滑方程所依据的理论主要是Reynolds润滑理论和Hertz 弹性接触理论，求解润滑中压力的分布规律，求得即在相互作用的圆柱和凸轮廓面挤压变形下油膜的厚度，润滑油粘度以及机构不同转速下，得出接触区比较重要的物理量参考润滑性能。忽略油膜的惯性力和速度在厚度方向的变化，只考虑油膜接触压力在速度方向的变化，结合一般形式的Reynolds 方程变换和赫兹接触公式可得到弹流润滑模型，即

式中：ρ为润滑油在压力p时的密度，h为油膜厚度，η为润滑油在压力p时的粘度，u为x方向速度，W为施加于接触线的载荷。

常使用Reynolds 的边界条件为

油膜厚度由2 个部分组成，一个是接触区的几何间隙，另一个是由于接触产生的压力下，滚子和凸轮廓面发生弹性形变，一般大小在微米级别。油膜厚度为

1.3 求解微间隙的理论基础

圆柱凸轮机构在啮合过程中，局部出于受载而产生了弹性变形，尤其是在滚子啮合发生交替的情况下更甚，且在交替的过程中，一个滚子的啮入和另外一个滚子的啮出，此时接触面的应力状况复杂，同时伴随着振动和变形，本文分析中忽视了弹性插销和动力轴等部分的变形，仅仅考虑柔性体滚子的变形对圆柱凸轮机构传动的影响。拟啮入的滚子由于前运行滚子的变形使得原本预定的轨道发生了偏移，在滚子驶入原来预定的轨道，此时2 曲面早已失去了原本的空间曲面啮合的条件，使啮合点延后，在廓面的入口处发生了切割，使滚子的表面出现划痕，从而引入非常大的干扰和不稳定项，传动机构在运行的过程中，将产生强烈的振动和噪声，也影响了其传动的准确度和稳定性。

横越冲击常出现在几何封闭环境内，例如圆柱凸轮机构，通常是接触路径中存在间隙，在机构的高速作用下（见图2），在接触时与非工作面冲击，产生严重的磨损。产生的横越冲击，根据动量定理可知

图2 滚子与带间隙的凸轮槽的啮合情况

式中：φ(t0)为路程函数泰勒展示的第4 项系数。

从式（6）可以得出，冲击载荷随滚子与2 侧廓面的间隙量、加速度的变化率、包括从动盘在内的后端负载的变化而发生改变，如果工况复杂且负载量大，增加滚子与2 侧廓面的间隙会增大横向冲击。尽管考虑了油膜的润滑作用，但长期的碰撞和摩擦下局部升温，使工作环境恶化，在负载的作用下又会减速直至重新与廓面接触从而输出驱动力，在反复的过程中滚子与左右廓面多次碰撞发生冲击影响着传动的稳定。

基于以上分析，为了解决上述问题提出一种引入耦合弹性变形与油膜厚度圆柱凸轮廓面2 侧间隙的方式：

1）每个滚子与左右2 廓面之间的法向间隙之和相同，即δ0=δ1+δ2相等。

2）滚子与左廓面（顺时针旋转）法向间隙的值取决于滚子所处的啮合位置，且为线性关系，最大值为啮入时刻，最小值为啮出的时刻。当机构反向旋转时，与另一侧间隙同上描述。

3）为了保证凸轮廓面的可加工性，廓面误差最小，在每个滚子的所有啮入高度上都引入滚子中心沿接触角θ=θ（h/2）的间隙。

引入间隙需同时考虑上述2 种出现不稳定因素的情况，假设滚子1 在刚啮入的转角位置，滚子2 与左廓面的间隙为δ1为总间隙的一半，选取滚子2 变形最大的时刻，故对于间隙最大数值设计限制为

式中：δt为滚子2 的变形值，δ3为滚子2 在从动盘处于图2 所示位置角的接触区域油膜的平均厚度，δ4为滚子1 接触区域油膜的平均厚度，δ0为所设间隙量最大值。

结合所建立的Reynolds 方程、油膜方程、载荷平衡方程求解，在上述求解过程中存在多个互相联系的未知量，且在上述方程中包含多个非线性解析式，无法得到解析解。对于滚子弹性变形量在复杂的接触环境下无法得出一组解析解，故求取微间隙的最优数值需通过仿真求解未知量的数值。

2 最优间隙量的求解

2.1 模型的有限元分析

本文关注的重点在于滚子与圆柱凸轮廓面接触区域的载荷和应力情况，故在建立分析模型时做了一些简化。比如滚子数量减少为2，仅在3 滚子同时啮入的情况使用3 滚子求解18°即可获得完成的分配情况，在载荷变化明显的位置还可以细分；设置即将啮入的滚子为滚子1，正在接触的滚子为滚子2，即将啮出的滚子为滚子3，后续都采用一样的指代。以滚子2位于角度0°为例，求解该位置接触区域的应力和载荷情况。在这里定义圆柱凸轮材料结构钢的数据为：弹性模量E=2.1×108Pa，泊松比μ=0.28，材料密度ρ=7 850 kg/m3。滚子与从动盘使用滚动副连接，滚子与凸轮之间施加接触条件，同时施加机构的运行负载M=1×106N·m。最终滚子与凸轮廓面接触情况展示如图3 所示。

图3 Ansys 的求解结果

滚子1 此时综合受载为1 133 N，滚子2 综合受载为4 741 N，最大应力位于滚子2 上，为424.3 MPa，根据该组结果调整从动盘的运行角度，其他不变，计算2滚子之间的受载情况与滚子2 的分配系数K，如图4 所示，具体数据如表1 所示。

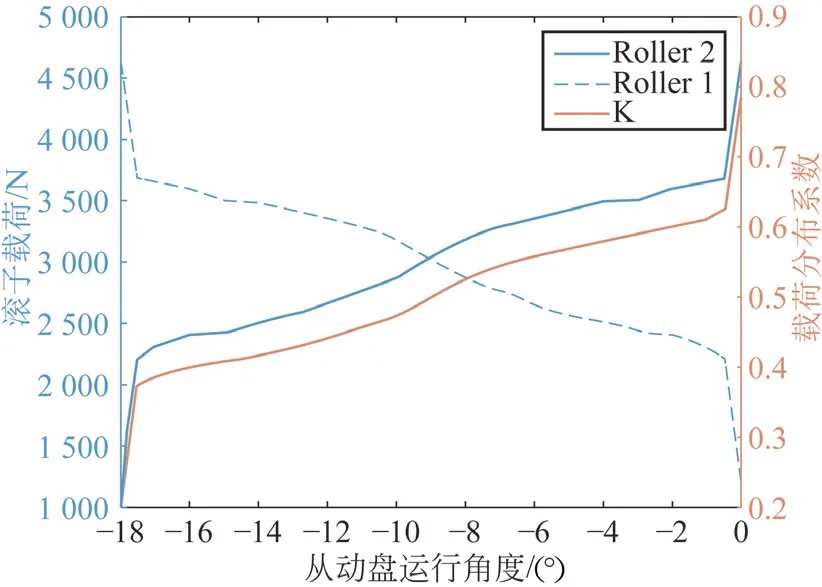
图4 双滚子之间的载荷分配

表1 清晰地展现了圆柱凸轮连续传动机构在运行中2 滚子的载荷分布情况，-18*表示3 滚子啮合的情况，可知在啮入的时刻滚子2 受到最大的载荷变化幅值也是最大的一段，其他时刻尽管滚子2 的载荷由2 215 N 到3 646 N，但过渡平缓，此处的3 滚子啮合情况还是在理想条件下求解的属于静力学分析的范畴。

2.2 数值求解

在上述数值模型中，存在着多个二阶非线性的成分，在数值求解的过程中，必须全部化为一阶线性的形式才能在计算机得到高效准确的计算结果，故须将方程组无量纲化和离散化处理。从上述方程中可看出，求解主要在于油膜压力的迭代、载荷收敛的准则和油膜厚度的修正。因此，本文决定使用黄平的弹性流体动压润滑（弹流润滑）的数值计算方法，即逐点压力迭代的方法进行计算，并应用多层网格法计算数值积分可有效解决计算量过大的问题[8]，最终结果以滚子2 啮合处及其附近的压力和油膜厚度为例，结果如图5 所示。

图5 滚子2 接触区域的油膜厚度与压力

2 个滚子最小油膜厚度都出现在出口区附近，在Hertz 接触区，油膜厚度基本上变化不大近似于一条直线，压力的骤降，在滚子出口区附近油膜收缩，此处是接触区域内膜厚最薄的地方。对于间隙的求解式所求结果为：δ2=5.29×10-7m，δ3=6.74×10-7m。

对于滚子2 的变形量求解，使用有限元仿真来模拟圆柱凸轮传动机构位于双滚子过渡到3 滚子的时刻，此时假定由于滚子2 的变形，滚子1 没有啮入，滚子2 与3 和圆柱凸轮接触，使用静力学结构分析求解滚子2 的变形可近似为实际工作中滚子2 的变形，结果如图6 和图7 所示。

图6 滚子2 在Z 方向变形量

图7 凸轮廓面与滚子2 接触区域在Z 方向变形量

根据仿真情况，滚子与廓面之间都存在Z反方向上的位移量，原因是凸轮锁定，施加沿着Z反方向的载荷使滚子与凸轮廓面同时变形，并同时向该方向挤压，依据Hertz 接触的特点，在接触半宽区会有一段变形量，以接触点处的法向上的位移为变形量，根据图6 和图7有着明显的赫兹接触区，但是Y方向比较杂乱且数值在0.01 μm，可忽略。由于接触边界不明显，图7 还需要拉取刻度条，将滚子变形图和廓面的变形图等值线拉到近似于接触线区域，最终求得滚子的变形量为2.8 μm，该变形量的求解更多依靠对Ansys 软件的熟练度和操作，对接触线位置会有部分预估。根据式（7）可得最大间隙量为4.6 ～5.8 μm。

2.3 圆柱凸轮传动机构的动力学分析

圆柱凸轮传动机构在运行过程中，滚子的变形使得机构在双滚子接触过渡到3 滚子接触过程中，在啮合处将产生突变的极大应力状况，内部存在极大的非线性接触属性，而非线性接触的预应力静力学将其转化为线性接触，静态力学的分析更多的是在频域内进行分析而非时域。因此，在对于非线性接触的分析中，线性的分析不允许解中包含非线性，但它在动态问题的解决上仍具备一些参考作用，它基于小变形理论，假设位移足够小，因而产生的刚度变化是微不足道的，接触面积也保持固定，脱离接触引起的振动是不存在的，且材料也遵循线性方式响应，但如果这些假设都极大不成立，则非线性的瞬态分析（Transient Structual）就是必要的，进而增加了大量的计算成本。

本文将使用Ansys 的瞬态动力学模块验证完全法使用完整的刚度质量与阻尼求解方程，它允许解中包含非线性的部分，故将选取完全法作为瞬态动力学分析的方法。仅考虑一个滚子从啮入到啮出的全部过程，根据设置的主动轮即圆柱凸轮的速度为600 r/min，计算一圈半所花时间为0.15 s，最终仿真得到了关于圆柱凸轮连续传动机构含间隙与不含间隙的最终接触应力数据如图8和图9 所示。

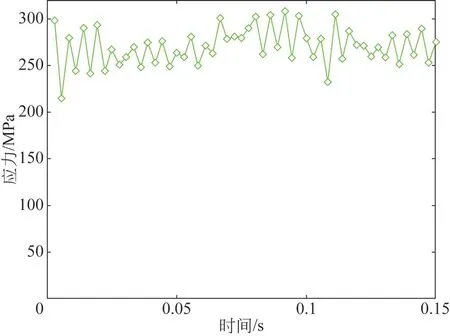
图8 无间隙圆柱凸轮机构工作廓面的接触应力具体数据

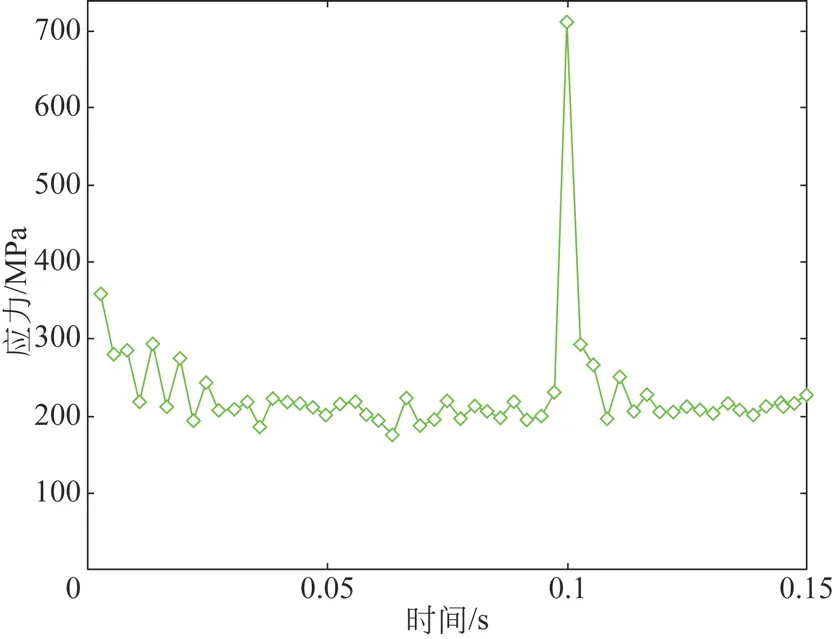
图9 含间隙圆柱凸轮机构工作廓面的接触应力具体数据

在含间隙的圆柱凸轮机构的接触应力与图相比，此时位于0.1 s 位置的峰值消失，但啮合位置发生偏差，整体应力情况波动浮动明显比无间隙的圆柱凸轮机构要强，应力值的分布更为平均，无间隙的机构的最大应力广泛分布于凸轮外圆边沿处，说明按本文引入的间隙方式和间隙量的圆柱凸传动机构虽然增加了一些应力的波动起伏，但对啮入的冲击却改善极大。此外，该种仿真忽略了关于油膜这类流体在机构运转过程中的作用，还需要耦合润滑油进行综合分析，故后续将进行基于港口设备实验平台现场于门座起重机运行时振动的影响测试。

3 实验测试平台设计与结果分析

3.1 实物研制

过去受制于加工机床的加工精度无法达到要求，在各类箱体的加工过程中需确保其空间坐标体系（线、孔、面）相互垂直、平行的精度≤0.01 mm，即箱体上各端面上的轴承支撑孔的同心度≤0.01 mm，是整个机加工领域难以突破的技术瓶颈，近年来由于技术突破，通过改造的国产立式加工机床可实现高精度盘类零件加工。

整个工件加工完毕后，不能立即使用，还需要先进行安装与调试，整个加工过程中不免会产生原始几何误差，且还存在装配过程中的误差，对于装配精度要求非常高。不同于齿轮之间中心距可以微调，圆柱凸轮传动机构的基距与中心距影响滚子之间的接触角，即不同位置的接触角不同导致机构失去啮合条件，从而使滚子2面受力，发生挤压变形卡死槽道。最终的装配经验是在安装中先保证中心距处的精度，最后调整基距，安装的位置选择设定的初始位置，如图10 所示。

图10 圆柱滚子与凸轮的装配

润滑油型号选择根据减速器作业环境、载荷大小的不同、运动特点以及摩擦形式的不同决定。按说明书要求选用粘度级在ISOVG100，实验平台选择长城润滑油4408（100 号）合成重负荷工业齿轮油，在项目运行阶段，通过电动机反复运行、试验，确定运行无碍后，将其安装到测试大车机构上，并观察测试大车运行过程中，电动机电流、噪声、振动等进行测试，并对各项参数进行比对。在实验过程中反复调试，待整机运行过程传动平稳。一组在制造中含间隙量为5 μm，另外一组加工方式为传统的机床加工，对于廓面加工误差比较高，所测间隙量为10 μm，鉴于成本考虑，只设置了1 组作为对照来对比最终的效果。

3.2 圆柱凸轮减速器的振动实验

如图11 所示，在港口综合实验平台现场进行2组减速器对应2 台门座起重机运行过程中振动的影响测试。

图11 港口综合实验平台现场

在测点的选取上选择靠近司机室一侧的出口处，使用的测试工具分别为：ECON 数据采集与分析仪器1 套，加速度传感器的参数为：数据采样率1 280 Hz、分析频宽500 Hz、采样点数2 048，测试传感器为185TNC 型加速度传感器，轴向灵敏度50 mV/g，量程100 g、频率范围0.5 ～5 kHz。圆柱凸轮减速器参数分别为：滚子数20、基距100 mm、中心距175 mm、滚子半径16 mm、滚子长度20 mm、从动盘节圆半径175 mm。实验平台工作参数如表2 所示。

表2 港口综合实验平台的主要技术参数

最终使用加速度传感器经过测得2 组减速器在测点处的振动，通过数据采集和分析处理，最终得到了每组减速器的振动波形图如图12 所示，其中，门座起重机1 对应的是含10 μm 间隙的圆柱凸轮减速器的波形图，门座起重机2 对应的是间隙量为5 μm 间隙的圆柱凸轮减速器波形图，取5 组波峰值，测试数据对比表如表3所示。

表3 测试振动数据对比表

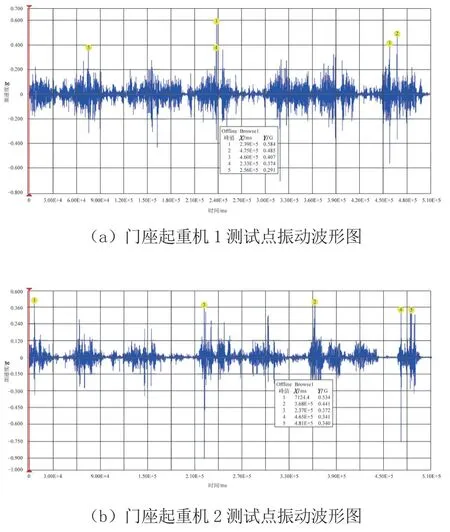
图12 天津某门座起重机振动测试图

根据上述数据，使用圆柱凸轮减速器（间隙值为10 μm）的门座起重机振动平均峰值为0.447，而使用本文计算求得的间隙量的圆柱凸轮减速器的门座起重机振动平均峰值为0.406，在原来的基础上更进一步将峰值平均值降低9.2%，提高加工精度，降低加工间隙，采用更合适的间隙量，会增强工作性能，降低振动，使晃动幅度进一步减小。

4 总结

1）将圆柱凸轮传动机构平稳性分析综合考量润滑油膜的作用和动态运动的过程中滚子的变形两者综合作用，建立了圆柱滚子接触区域的弹流润滑方程组，并结合有限元分析软件的仿真数据得到了弹性滚子的变形量，并建立了方程的边界条件采用多重网格法与压力迭代法求解了润滑油膜的厚度以及滚子的平均变形量，进而求得圆柱凸轮传动机构间隙量的理论最优解。

2）使用这种耦合微变形与润滑油膜的圆柱凸轮廓面两侧间隙量的计算方法，并建立含有该间隙量的圆柱凸轮传动机构的三维模型，在Ansys 的动态仿真中能发现相较于无间隙的一组，虽然增加了一些起伏，但是消除了滚子啮入时极大的应力，减缓了冲击，提高了运行的稳定性。

3）将该方法运用于港口机械上，最终得出了耦合最优微间隙的圆柱凸轮减速器在实际运用场景下能有效提升传动平稳性和减小振动。