基于Abaqus 的索道有限元模型及参数研究*
李玉彤 伍希志 谢 言 薛 洋 贾 惠
中南林业科技大学材料科学与工程学院 长沙 410004
0 引言
索道作为一种便捷、可靠的运输方式,能适应复杂的地形,跨越山川河流,克服恶劣条件,因而被广泛应用于林业、风景园区、矿业生产等领域。相比于其他运输方式,索道架设方便快捷、成本较低。索道的使用寿命和安全运行是其运行的关键因素。钢丝绳的应力应变、索道架设的挠度、支点的受力对索道的使用寿命及安全有很大影响。
众多学者对索道钢丝绳进行了广泛研究。在短钢丝绳研究上,马军、葛世荣、张德坤等[1-3]利用Ansys 研究了短钢丝绳内载荷的分布、丝间应力的分布、钢丝绳微动磨损规律等;姜海波等[4]分析了在短钢丝绳内接触因素对其应力分布的影响;沈燕等[5]研究了在短钢丝绳接触载荷上对其磨损的影响;张家铭[6]在研究了短钢丝绳内缠绕钢丝绳的力学性能;杨柳[7]研究了短钢丝绳在常温下的蠕变性能。在长钢丝绳研究上,孙海晶等[8]简化了长钢丝绳弹性伸长的总体计算;邓润基等[9]研究了长钢丝绳内静力构型与内力计算;刘媛媛[10]研究了利用检测技术对长钢丝绳损伤进行判别;刘兆宇等[11]提出了按影响因素对长钢丝绳进行合理周期监测;张飞凯等[12]提出基于Dijkstra 算法的货运索道路径规划方法。目前,采用有限元方法对长距离索道挠度及其支点受力进行研究较少。
本文以1×19IWS 钢丝绳为研究对象,采用接触方式模拟钢丝之间的传力关系,建立了短钢丝绳的精细有限元模型,计算了钢丝绳的弹性模量;采用梁单元模拟钢丝绳,建立了索道承载索的有限元模型,并与悬索抛物线理论进行对比验证;采用索道有限元模型研究了跨距、载荷、温升等参数对索道受力的影响。
1 悬索的抛物线理论
由于钢丝绳具有柔性,在自重的作用下索道线型呈悬链线形状。自悬链曲线问世以来,很多学者研究了悬链曲线的理论解,先后提出了抛物线理论、悬索曲线理论、摄动法理论。目前最普遍使用的是抛物线理论[13]。
图1 所示为无荷抛物线悬索,严格意义上钢丝绳的自重是沿其本身长度均匀分布,由于钢丝绳线型是接近于直线的平缓曲线,可以将钢丝绳的自重视为沿x轴方向均匀分布垂直荷重,此时绳索的曲线理论即为抛物曲线。
悬索曲线的方程为式
此状态下的悬索曲线线形为抛物线。曲线上任一点挠度为
当x=l/2 时,有悬索中央挠度为
无荷中央挠度系数为无荷中央挠度与水平跨距的比值,即
在索道关系中,挠度系数s常用来表示悬索张紧的强弱程度。
用修正的负载状态的补正挠度系数s'代替原来的挠度系数s,从而能求得考虑弹性伸长影响的计算值。将补正值与原来挠度系数的比值称为挠度补正系数,即
在荷重、温度、跨距等条件变化的情况下,求其对应的补正系数ε
如索长为L,且张力增加了ΔTm,则弹性伸长
式中:λ为单位张力所对应的弹性伸长率。
式中:E为弹性模量,A为金属截面积。
如索长为L,且温度上升Δt,则弹性伸长
式中:ω为钢丝热膨胀系数,ω=11×10-6/C°。
设无荷挠度系数为sⅠ的悬索上作用集中载荷,同时加上支点位移、温度变化、钢索向跨内窜移等因素,补正挠度系数为sⅡ。原无荷索长为
式中:u为跨距弦长,u=lsecα。
此时,悬索因集中载荷而产生弹性伸长量、非弹性绳索伸长量、弦长缩短量等。此时比较无荷索长与负载索长,则两端固定式的悬索可表示为
平均张力可表示为
无荷索平均张力为
式中:GⅠ为无荷索的荷重系数。
有荷索平均张力为
式中:GⅡ为载荷索的荷重系数。
由此,弹性伸长量为
整理得补正系数的方程为
式中:q为单位长度承载索的重力
2 索道的有限元模型
2.1 索道有限元模型建立
由于索道跨度远远大于钢丝绳截面,在进行长跨度的挠度、预拉力等分析时,将钢丝绳视为一种连续介质材料,即截面不存在间隙,建立力学求解模型。图2 为实际钢丝绳与力学模型对比。
索道的有限元模型采用梁单元,此单元可以承受拉、压、弯曲及大变形等。本文索道跨距为400 m,索道始末高度差为80 m,即索道弦倾角约为11.537°。钢丝绳采用28 mm 的天然纤维芯,参考质量275 kg/100 m,截面积292 mm2,钢丝绳弹性模量参考2.2 节。载荷只考虑自重载荷和集中载荷。约束条件为固定钢丝绳左端,在右端施加x方向拉力并约束其余5 个自由度,拉力大小取46 789 N。图3 为索道的有限元模型。

图3 索道的有限元模型
2.2 钢丝绳弹性模量
在SolidWorks 中建立钢丝绳几何模型,再导入Abaqus 中,特征参数钢丝绳直径d为22 mm,中心钢丝直径为5.82 mm,内层钢丝直径为3.02 mm,外层钢丝直径为5.61 mm,捻距为78 mm,钢丝弹性模量E=200 GPa,泊松比为0.3。钢丝绳几何模型如图4 所示。

图4 钢丝绳几何模型
短钢丝绳精细有限元模型如图5 所示,由于钢丝绳是钢丝螺旋缠绕而成,钢丝之间存在相互接触,采用通用接触方式以简化接触设置的前处理时间,相邻钢丝间的法向接触属性设置为硬接触,切向接触属性设置为无摩擦。这样设置是因摩擦力仅对局部接触区域应力有较大影响,对钢丝绳整体力学行为影响可以忽略。钢丝网格单元使用沙漏控制缩减积分的8 节点体单元C3D8R[14,15],同时为了减少计算量和仿真时间,以中性轴算法在轴向和周向上进行网格划分。载荷与边界条件设置:将钢丝绳两端端面的节点分别进行耦合,参考点RP1 耦合的端面为固定端,对其6 个自由度进行约束;参考点RP2 耦合的端面为受力端,对其除轴向移动外的其余5 个自由度进行约束,并对其参考点施加沿轴向方向的载荷,载荷大小为50 kN。

图5 短钢丝绳的精细有限元模型
短钢丝绳的有限元仿真结果如图6 所示,可知:

图6 短钢丝绳的有限元仿真结果
1)钢丝绳外表面的等效应力为非均匀分布,等效位移从加载端到固定端依次减小。
2)绳股截面内的等效应力呈中心对称状分布,靠近接触点应力较大,远离接触点应力较小,接触点应力大小由内向外逐渐递减,最大应力位于中心钢丝与内层钢丝接触点处,外层钢丝外侧的应力最小,即钢丝绳芯承受更大的应力。
3)钢丝的变形由内向外逐渐增大,即外层钢丝变化幅度大于内层钢丝变化幅度,内层钢丝变化幅度大于中心钢丝化幅度。
4)内层钢丝和外层钢丝的应力沿钢丝绳长度方向呈螺旋状分布,且接触区域应力较大。
根据国内外学者研究,钢丝绳的弹性模量一般取(1.1~1.2)×105MPa[16]。为了获得钢丝绳的弹性模量,对钢丝绳有限元模型施加不同的轴向载荷,得到相应的轴向位移,根据钢丝绳实际弹性模量的测定方法对仿真的钢丝绳进行弹性模量的计算。分别取轴向载荷为50 kN、100 kN 和150 kN,分别得到轴向位移0.076 mm、0.149 5 mm 和0.221 9 mm,利用弹性模量公式E=(F2-F1)L/[S(dL2-dL1)]进行计算,求得弹性模量为1.163×105MPa、1.181×105MPa ,取其平均值钢丝绳的为1.172×105MPa ,计算结果与其他学者的研究相符合。
2.3 索道仿真模型验证
为了验证索道仿真模型,将仿真模型与抛物线理论计算结果进行对比。假定索道跨距为400 m,高度差为80 m,索道预紧力为55 000 N,温度不变,处于索道中央位置。图7a 所示为不同载荷情况下中央挠度的误差曲线,图7b 所示为不同载荷情况下上下支点力的误差曲线。
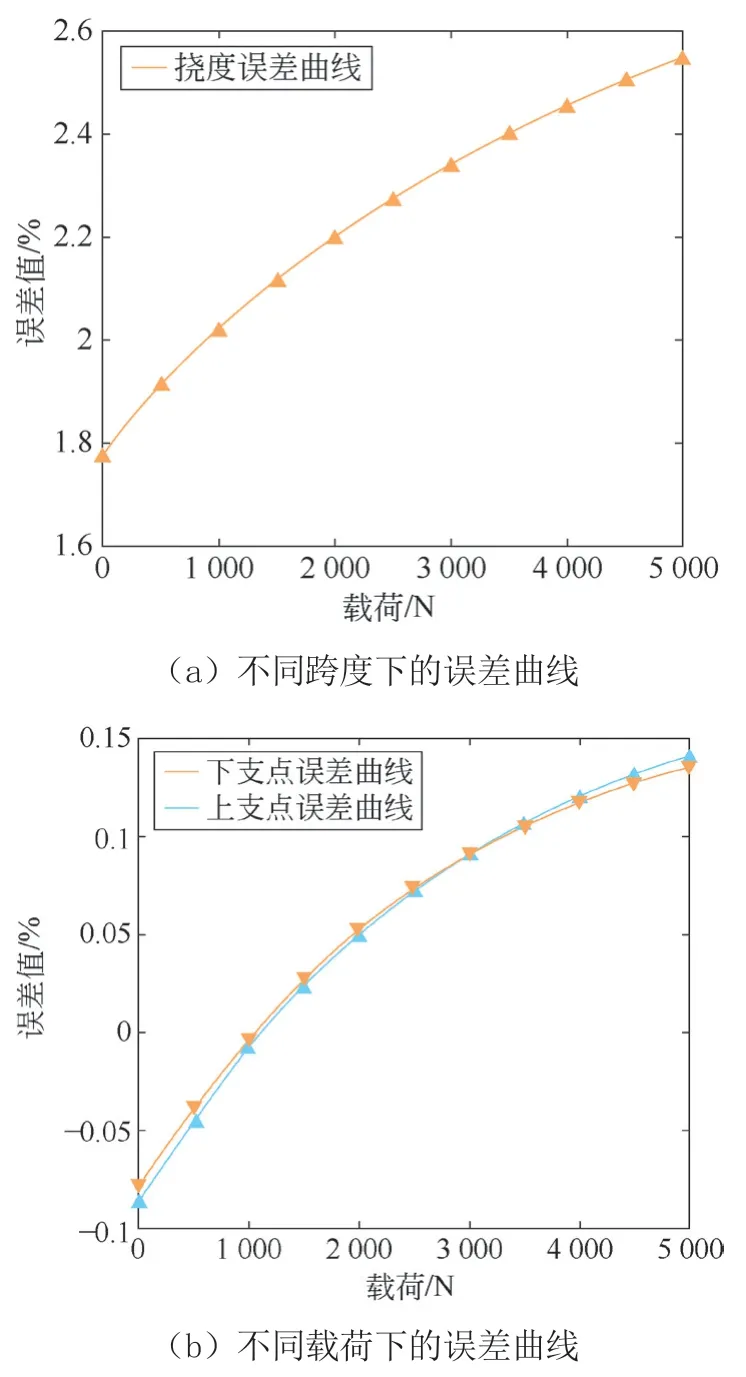
图7 索道仿真模型与抛物线理论的误差曲线
由图7a 可知,在载荷范围0 ~5 000 N 内,随载荷的增加,中央挠度的仿真与理论误差值逐渐增加,增幅逐渐减小。当载荷为5 000 N 时,误差值达到最大,为2.55%。由图7b 可知,随着载荷的增加,上下支点力的仿真与理论误差值逐渐增加,增幅逐渐减小。当载荷为5 000 N 时,误差值最大,分别为0.14%、0.13%,上支点的误差略大于下支点的误差。总之,索道仿真结果与理论数值基本相符,证明Abaqus 梁单元可以很好地模拟索道受力。
3 参数分析
3.1 跨距
研究索道跨距对挠度和支点受力的影响。设索道高度差为80 m,载荷为5 000 N 并处于索道中央位置,索道预紧力为55 000 N,温度不变,只改变索道的跨度。图8a 为不同跨度下索道1/8 处、1/4 处及中央的挠度值曲线,图8b 为不同跨度下索道上下支点力曲线。
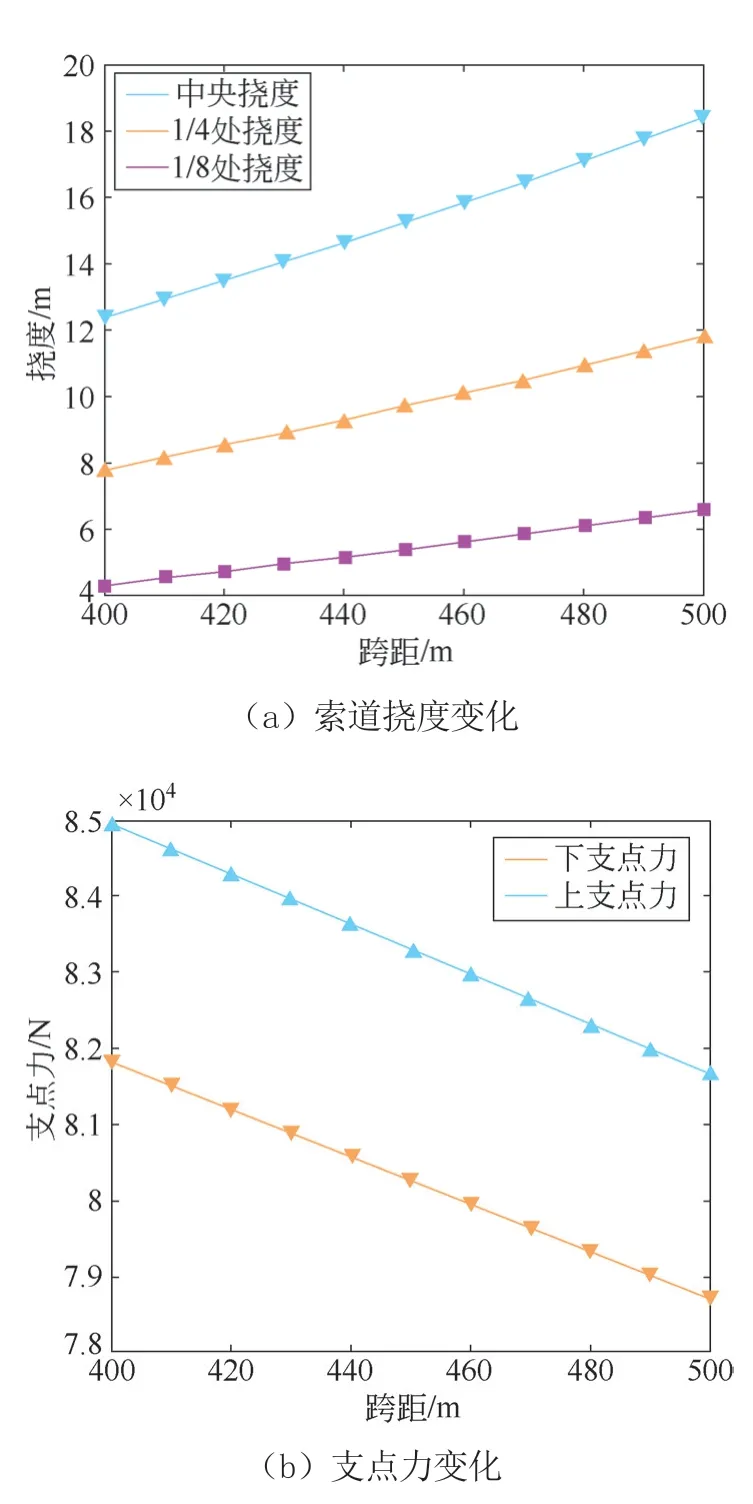
图8 跨距对索道的影响
由图8a 可知,随索道跨度的增加,所有节点挠度值基本呈线性增大。当索道由400 m 增大到500 m 时,1/8 节点处挠度增大了2.47 m,1/4 节点处挠度增大了4.21 m,中央挠度增大了5.63 m,挠度增幅由索道中央向两侧逐渐递减。由图8b 可知,随跨距增加,支反力也逐渐增加,两者基本呈线性相关。跨距由400 m 增大到500 m 时,支反力增加了149.7 N。增加幅度较小。
3.2 载荷
研究载荷对挠度的影响,现只研究载荷位于索道中央时的情况。现假定索道跨距为400 m,高度差为80 m,索道预紧力为55 000 N,温度不变,只改变索道的载荷。图9a、图9b 和图9c 分别表示不同载荷下索道1/8 处、1/4 处及中央的挠度值曲线,图9d 表示不同跨度下索道上下支点曲线。


图9 载荷对索道的影响
由图9 可知,随着载荷的增大,各节点的挠度变化规律不同,在1/8 处,挠度值随载荷的增加先减小而后增大;在1/4 处,挠度值随载荷的增加逐渐增大,基本呈线性相关;在中央处,挠度值随载荷的增加逐渐增大,但增幅程度逐渐减弱。总之,载荷越大索道挠度越大。由于悬索自重和负载的双重作用,负载两边悬索趋向弦线状态,在负载较小时,1/8 节点处挠度会随载荷增加而减小。随载荷增加,上下支点力也逐渐增大,两者基本呈线性相关,载荷由0 增大到5 000 N 时,支点力增大了39 692.4 N,增大幅度大。
3.3 高度差
研究索道高度差对挠度和拉力的影响。现假定索道跨距为400 m,载荷为5 000 N 并处于索道中央位置,索道预紧力为55 000 N,温度不变,只改变索道的高度差。图10a 为表示不同载荷下索道1/8 处、1/4 处及中央的挠度值曲线,图10b、图10c 为不同跨度下索道上下支点力曲线。图10d 为表示仿真和理论的上支点力随弦倾角度的变化规律。

由图10a 可知,随着高度差的增大,各节点的挠度逐渐增大,中央挠度增大了0.225 m,1/4 处挠度增大了0.129 m,1/8 处挠度增大了0.097 m,基本呈线性相关,挠度增幅由索道中央向两侧逐渐递减。由图10b、图10c 可知,随着高度差的增大,索道下支点力逐渐减小,从85 201.30 N 减小到80 826.10 N,减少了4 375.20 N,基本呈线性相关;索道上支点力先增大而后减小,在高度差20 m 左右达到最大。这是由于索道在上支点的斜率随高度差的增大而逐渐增大,在下支点处的斜率变化十分微小,可忽略不计。由10d 可知,索道上支点力与弦倾角有着一定的关系,接近于二次函数,在弦倾角5°左右时,上支点力达到最大。
3.4 预紧力
研究索道预紧力对挠度和支点受力的影响。现假定索道跨距为400 m,高度差为80 m,载荷为5 000 N 并处于索道中央位置,温度不变,只改变索道预紧力。图11a 为不同载荷下索道1/8 处、1/4 处及中央的挠度值曲线,图11b 为不同跨度下索道上下支点力曲线。
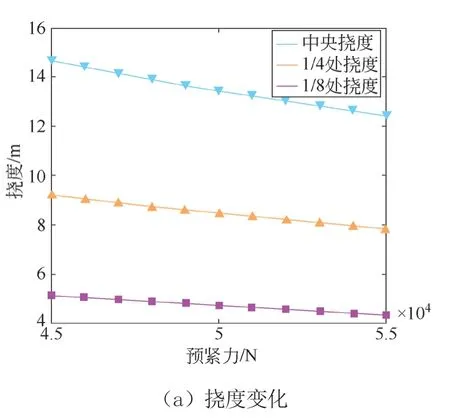
图11 预紧力对索道的影响
由图11a 可知,随着预紧力的增大,各节点的挠度逐渐减小,中央挠度减小了2.21 m,1/4 处挠度减小了1.41 m,1/8 处挠度减小了0.81 m,基本呈线性变化,挠度增幅由索道中央向两侧逐渐递减。随着预紧力的增大,索道上下支点力随之线性增大,预紧力由45 000 N增大到55 000 N,上支点力增大了12 400 N,下支点力增大了12 399.4 N,上下支点力增幅基本相同。
3.5 温度
研究温度对挠度及拉力的影响。设索道跨距为400 m,高度差为80 m,预紧力为55 000 N,载荷为5 000 N 并处于索道中央位置,只改变温度。图12a 为不同载荷下索道1/8 处、1/4 处及中央的挠度值曲线,图12b为不同跨度下索道上下支点力曲线。
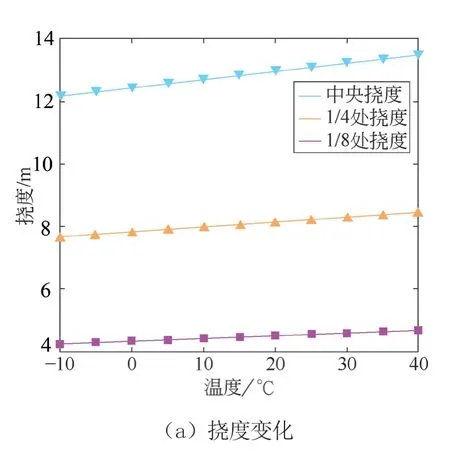
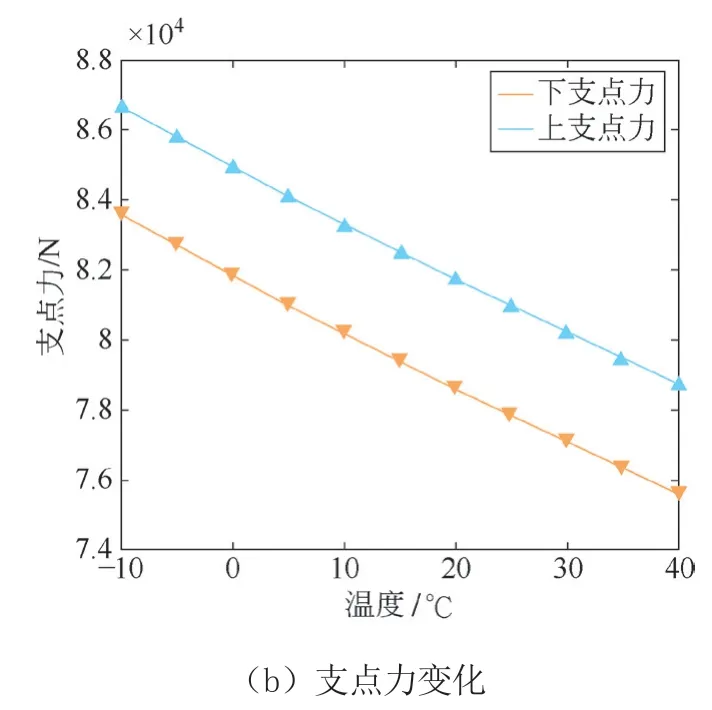
图12 温度对索道的影响
由12a 图可知,随着温度的升高,各节点处挠度逐渐增大,中央挠度增大了1.252 m,1/4 处挠度增大了0.776 m,1/8 处挠度增大了0.424 m,基本呈线性变化,挠度增幅由索道中央向两侧逐渐递减。由12b 图可知,随着温度的升高,索道上下支点力随之减小,基本呈线性变化,上支点力减小了7 892.5 N,下支点力减小了7 892.2 N,幅度变化基本一致。
4 结论
建立短钢丝绳的精细有限元模型,由有限元分析可知,不同的钢丝等效应力均随捻制方向螺旋分布,钢丝截面应力呈中心对称分布,得到钢丝绳的弹性模量为1.1×105MPa,与其他学者的研究相符合。建立索道承载索的有限元模型,与悬索抛物线理论进行对比,仿真值与理论值误差小于3%。
利用索道有限元模型研究了跨距、载荷、高度差、预紧力、温度5 个因素对索道挠度及支点受力的影响。在对索道挠度的影响上,跨距、高度差、温度三者与索道挠度基本呈正线性相关;预紧力与索道挠度呈负线性相关;载荷与索道挠度呈正相关性,但各点处呈非线性变化。在对索道上下支点力的影响上,跨距、载荷、预紧力三者与索道上下支点力均呈正线性相关;高度差与上支点力呈非线性变化,与下支点力基本呈负线性相关;温度与上下支点力呈负线性相关。
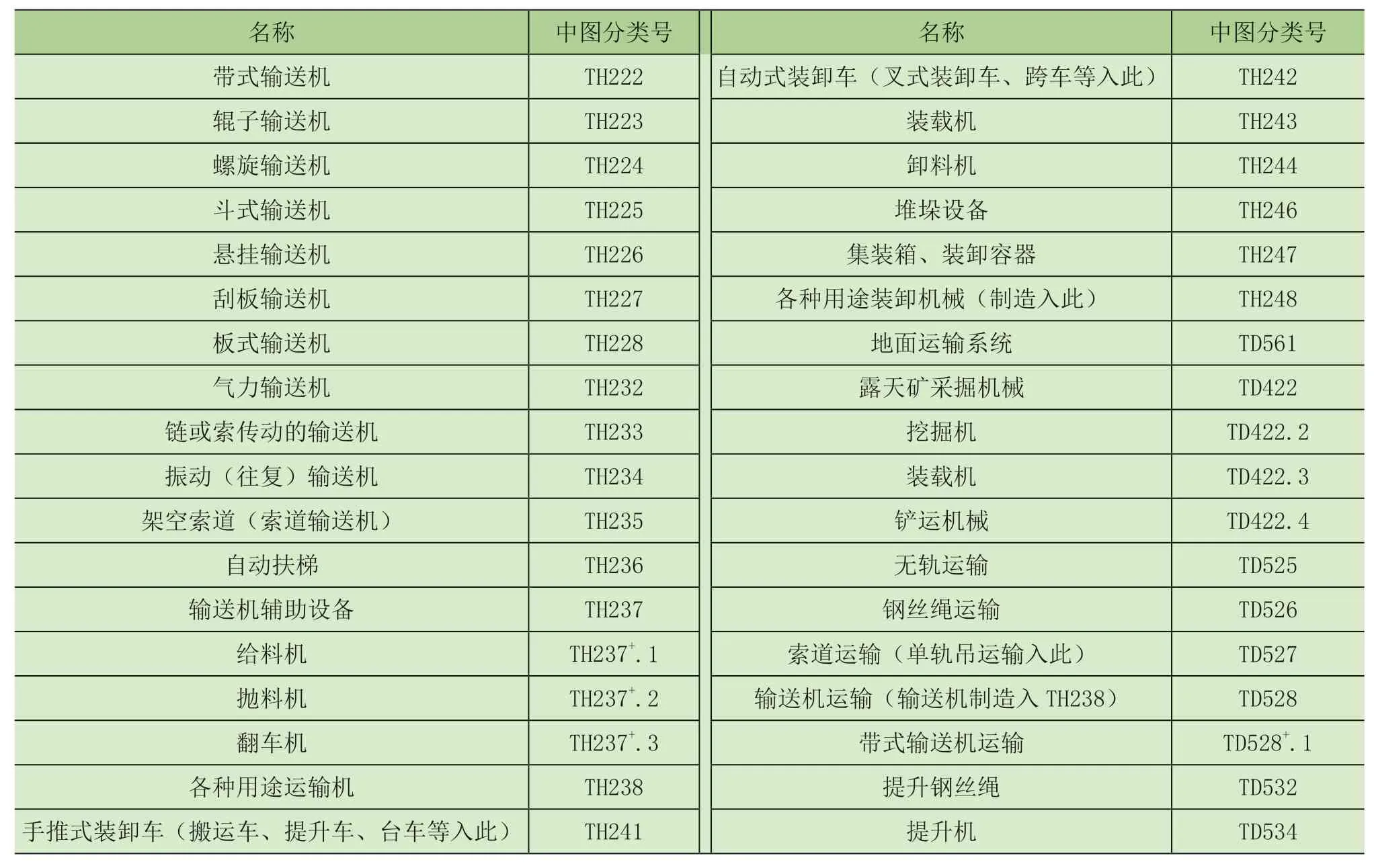
部分常用中图分类号——输送机械类

