基于Ansys 带式输送机驱动装置架动态特性分析

姚艳萍 张 玺 程泽鹏 田星宇 李金泊

太原科技大学机械工程学院 太原 030024

0 引言

随着高产高效矿井的发展，原有带式输送机的主参数、运行性能等都已不能满足要求，必须向长距离、高带速、大运量、大功率的大型化方向发展，要改善和提高运行性能，确保安全可靠[1]。驱动装置是带式输送机的动力来源，由电动机、减速器、联轴器、逆止器或制动器等组成。带式输送机的驱动装置架作为承载驱动装置的结构，除受到承载的重力之外，还受到电动机和减速器等的外部激励载荷，当激励载荷的频率接近钢结构的固有频率时会发生共振影响设备正常运行。为了避免共振对驱动装置架造成较大变形破环系统稳定性，进行模态分析得出支撑结构的固有频率和振型，分析受到外部激励时驱动装置架的振动趋势，然后进行谐响应分析得到频率响应曲线，为动态特性提供理论基础。

带式输送机向大型化发展，其主要零部件不仅要完成选型，还要进行必要的设计计算，对驱动装置架进行特定工况下力学分析特别是振动分析是十分有必要的。本文对原有使用的《DTII（A）型带式输送机设计手册》中驱动装置架的设计作了部分优化[2]，以Y—ZLY/ZSY板梁式驱动装置架进行研究，选用电动机型号Y225 M—4，减速器型号ZSY280。

1 驱动装置架强度刚度分析

1.1 实体模型和有限元模型建立

驱动装置架主要由上支架、下支架、连接件、支撑上下支架的槽钢和角钢等通过焊接和螺栓连接而成，其中上支架主要承载驱动装置，下支架螺栓连接固定在地面或相应的连接部位，上支架从左到右分别安装电动机、液力偶合器、制动器和减速器。利用SolidWorks 三维软件绘图时忽略倒角、圆角和对结构特性影响较小的螺纹孔、退刀槽等结构，简化模型提高求解效率。

在Ansys Workbench 软件中对驱动装置架进行有限元建模，图1 所示。选用Q235 钢材料，单元类型选择四面体单元（Tetrahedrons）划分网格，网格单元大小为15 mm，电动机承载等部位局部加密采用10 mm，应用Patch Conforming 算法，有限元模型弹性模量为210 GPa，泊松比0.28，质量密度为7 850 kg/m3，单元数为246 787，节点数为455 390[3]。

图1 驱动装置架模型图

1.2 载荷及边界条件施加

驱动装置架下支架固定在地面或相应的连接部位，将下支架设置为全约束。上支架承载驱动装置受到各部件的重力，由于驱动装置架各部位连接一般为焊接或螺栓连接，为了简化模型将各部位连接设置为绑定接触（Bonded）。机架受到电动机减速器传递的扭矩，此外制动器等也会产生对机架的作用力。

额定功率下电动机传递的扭矩为

式中：P为功率，n为转速。

减速器传递的扭矩为

式中：n1为电动机转速，i为速比，u为使用系数。

1.3 强度刚度分析

在实际工作中，驱动装置产生激励作用在驱动装置架上，产生变形的同时会影响带式输送机的传动性能，故分析驱动装置架在安全运行时产生的变形以及应力状况。通过有限元分析，得到驱动装置架的应力和位移分布云图。

图2 为机架的应力云图，最大应力为13.331 MPa，位于减速器安装区域，Q235 钢屈服应力为235 MPa，最大应力远小于屈服极限，结构受力满足刚度要求。由图3 机架位移云图可知，机架最大变形位于减速器区域承载处，为0.019 3 mm，机架整体变形较小，机架运行正常。

图2 驱动装置架应力云图

图3 驱动装置架位移云图

在进行驱动装置架整体静应力分析后，对上下支架螺栓连接处进行局部分析，发现最大变形和最大应力分别位于减速器上下支架螺栓连接处，满足驱动装置架整体强度刚度分析结果。为了增加系统稳定性，可采取预防措施提高螺栓连接强度。

2 模态分析

通过模态分析方法可以了解结构在某频率范围内的各阶主要模态的特性，使结构避免共振或让结构在指定的频率下振动，是动力学分析的基础。模态分析只与材料性能、结构形状和约束形式等有关，与载荷无关。

将下支架螺栓连接处设置为固定约束，对驱动装置架进行自由模态分析。结构的动态特性一般由低阶固有频率和振型所决定[4]。此次分析采取分块兰索斯法（Block Lanczos）[5]对驱动装置架前6 阶模态进行求解。模态分析用于确定结构的固有频率和振型[6]。驱动装置架前6 阶模态分析固有频率和振型描述如表1 所示。

表1 驱动装置架固有频率和振型

由模态分析结果可知，由于下支架螺栓连接固定在地面上，不易发生振动，上支架和中间支架容易发生弯曲摇摆和扭转。特别是上支架电动机与其他驱动装置连接处易发生变形，影响设备正常运行。电动机额定转速运行时激励频率为98.67 Hz，驱动装置架模态分析前6 阶频率较低，均小于电动机激励频率，易发生系统共振，模态分析结果为谐响应分析提供了重要的理论基础和依据。

3 结构优化改进

3.1 驱动装置架的结构优化

通过前文模态分析可知，下支架全约束在地面可以认为是固定不动的。为了增加机架的固有频率和改变电动机连接处的振型，在局部增加了刚性连接防止结构受到共振变形。在原机架支撑槽钢处左右各交叉焊接2 块长1.5 m，宽50 mm，厚20 mm 的钢板，电动机支架连接处连接了2 块折弯板，同时为了增加结构刚性，将部分角钢替换成20 mm 厚的钢板。优化后结构如图4 所示。

图4 优化后的驱动装置架

3.2 优化结构的模态分析

对优化后的结构做模态分析，由表2 可看出一阶模态频率由原始36.895 Hz 提高到了40.718 Hz，六阶模态频率由原始84.363 Hz 提高到了225.77 Hz，一阶模态振幅由3.2233 mm 减少到了3.0356 mm。提高了驱动装置架的固有频率降低了振幅。除了一阶、二阶固有频率之外其余固有频率均大于电动机激励频率，不在电动机产生的激励频率范围之内，系统不易发生共振。

表2 优化驱动装置架固有频率和振幅

4 谐响应分析

模态分析结果的位移值是一个相对的量值，它表征各节点在某一阶固有频率上振动量的相对比值，反映该固有频率上振动的传递情况,并不反映实际振动的数值[7]。为了得到机架在一个频率范围内的具体振动情况并得到机架关键节点沿各方向的位移－频率关系，还需要在模态分析的基础上进行谐响应分析[8]。

4.1 谐响应分析原理

模态振型图的位移值并不是实际的振动位移，它只是表征各节点在某一阶固有频率上振动量的相对比值。谐响应分析主要用于确定结构在承受简谐规律的载荷时的稳态响应，目的是计算结构在不同频率的响应值，从而使设计人员能预测结构的持续性动力特性，验证设计是否能克服共振、疲劳以及其他受迫振动引起的有害效果。

简谐激振力作用下，运动微分方程为[9]

式中：M为结构质量矩阵；C为结构阻尼矩阵；K为结构刚度矩阵；为位移的一阶导数，表示速度；为位移的二阶导数，表示时间；F(t)为随时间变化的载荷函数。

节点的位移响应为

式中：A为位移幅值向量，φ为位移响应滞后激励载荷相位角。

4.2 谐响应分析结果

根据模态分析结果，对驱动装置架的电动机和减速器支撑区域做谐响应分析。在电动机安装上支架施加水平沿Z轴350 N 和垂直沿Y轴负方向350 N 相位差90°的激励。减速器安装上支架施加水平沿Z轴750 N和垂直沿Y轴负方向750 N 相位差90°的激励。设置求解频率为40 ～230 Hz，为了使求解结果清晰明了，打开聚集结果（Cluster Nember），并且设置Clister Nember 为2，采用模态叠加法对驱动装置架进行谐响应分析。

1）电动机支撑架谐响应分析

电动机支撑架在X轴、Y轴、Z轴的振幅－频率响应曲线如图5 所示。X方向振幅峰值在111.28 Hz，Y方向振幅峰值在111.28 Hz，Z方向振幅峰值在40.709 Hz，对应驱动装置架模态分析的四阶和一阶固有频率，其中Z方向振幅最大为0.644 69 mm。

图5 电动机支架振幅－频率响应曲线

X轴、Y轴和Z轴的应力－频率响应曲线如图6所示。在X方向的应力峰值在111.28 Hz、在Y方向的应力峰值在110.73 Hz，在Z方向的应力峰值在40.709 Hz，对应驱动装置架模态分析的四阶和一阶固有频率，其中X方向所受应力幅值最大为6.3563×102MPa。

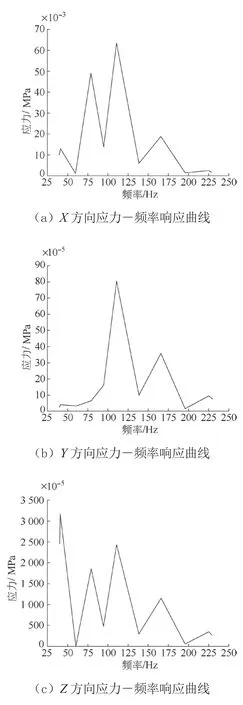
图6 电动机支架应力－频率响应曲线

根据振幅－频率响应曲线和应力－频率响应曲线可知，电动机支架在外界激振频率接近驱动装置架一阶固有频率时振幅幅值和应力最大。查看位移云图和应力云图可知，电动机支架区域最大变形为0.78973 mm，最大应力为23.738 MPa，小于材料屈服极限，结构满足设计要求。

2）减速器支架谐响应分析

减速器支架在X轴、Y轴和Z轴的振幅－频率响应曲线如图7 所示。X方向位移峰值在40.742 Hz，Y和Z方向位移峰值在79.346 Hz，对应驱动装置架模态分析一阶和二阶固有频率，其中Z方向振幅最大为0.333 92 mm。

在X轴、Y轴和Z轴的应力－频率响应曲线如图8所示。在X方向的应力峰值在110.19 Hz、在Y方向的应力峰值在79.41 Hz，在Z方向的应力峰值在79.346 Hz，对应驱动装置架模态分析的三阶和一阶固有频率，其中Z方向所受应力幅值最大为0.180 33 MPa。

根据振幅－频率响应曲线和应力－频率响应曲线可知，减速器支架在外界激振频率为79.457 Hz，即接近驱动装置架二阶固有频率时位移幅值和应力最大。查看位移云图和应力云图可知，减速器支架最大位移为0.556 51 mm，最大应力为44.347 MPa，分析可知实际应力较小结构满足设计要求。

5 结语

1）通过对驱动装置架进行静力学分析可知，驱动装置架在承受重力和扭矩的载荷作用下最大应力为13.331 MPa,最大变形量为0.019 3 mm，整体变形较小，满足机构运行情况。

2）通过对驱动装置架进行模态分析，得到机架的固有频率和振型，发现电动机支撑架连接处易变形，机架前6 阶固有频率都位于电动机激振频率范围之内容易发生共振。通过改进机架结构，提高了机架的固有频率，改变了机架振型。

3）重点对电动机和减速器承载区域做谐响应分析,分析可知电动机激励接近驱动装置架一阶固有频率（40.718 Hz）和二阶固有频率（79.457 Hz）时，系统发生共振时振幅和应力最大。通过分析振幅－频率响应曲线和应力－频率响应曲线，得到最大变形和最大应力，振幅和应力较小不超过材料屈服极限，相对于设计加工要求影响不大。