双螺旋互动：基于主线问题的数学教学新样态*

仇学春

《义务教育数学课程标准（2022 年版）》（以下简称“新课标”）指出：“通过对现实世界中基本数量关系与空间形式的观察，学生能够直观理解所学的数学知识及其现实背景；能够在生活实践和其他学科中发现基本的数学研究对象及其所表达的事物之间简单的联系与规律。”在数学教学中，教师不仅要观照学科逻辑，还要观照学生的生活逻辑，把它们有机结合起来，形成一种类似于DNA 模型的“双螺旋互动”教学模型。

一、双螺旋互动的内涵与要义

本文所说的“双螺旋”，一个是彰显学科逻辑的螺旋，另一个是彰显生活逻辑的螺旋，二者相互作用、相互促进，又螺旋上升，是一个动态机制。学科逻辑和生活逻辑围绕学习逻辑进行螺旋互动，形成了一个新的教学模型。（如图1）

（图1）

其一，学科逻辑。多数人把数学看成一种知识体系，是经过严密的逻辑推理而形成的系统化的理论知识总和。数学知识包括陈述性知识、程序性知识和过程性知识。陈述性知识也称概念性知识，解决“是什么”的问题；程序性知识也称方法性知识，解决“怎么做”“为什么”的问题；过程性知识也称体验性知识，解决“从哪里来”“到哪里去”的问题。如教学“百分数的认识”时，围绕“什么是百分数”这个核心问题，可以形成“知识从哪里来（百分数的起源）”“知识如何展开（百分数的意义）”“知识往哪里去（百分数的统计意义）”等具有学科逻辑的问题系统。

其二，生活逻辑。儿童学习会更多参照已有生活经验、生活经历和生活感悟，注重数学知识与生活现实的有机结合。生活逻辑不是简单的生活叠加，而是儿童在发现生活、理解生活和参与生活的过程中获得解决问题的经验、方法和智慧。生活逻辑的起点是大量的生活现象、生活素材，运用数学观点去解释生活现象、指导生活行为是生活逻辑的归宿。因此，生活逻辑就是生活现象向数学问题过渡的方法或程序。

除了学科逻辑和生活逻辑，我们还需要观照儿童的学习逻辑。儿童的学习逻辑经历“感性具体—抽象规定—思维具体”螺旋互动上升的过程。

二、主线问题的特征与价值

“双螺旋互动”的两条螺旋曲线由各种数学问题附着其上，问题拎起知识，思维从经验中提升，问题激发思维，思考产生新问题。其中，学科的核心问题、教师组织的探究问题和学生提出的日常问题组成了一条有逻辑关系的主线问题。主线问题就是把生活逻辑跟学科逻辑结合在一起建构出来的情境问题，是由核心问题串起来的一系列有逻辑关系的问题系统。主线问题通过“三问”（即自主提问、系统理问、互动追问）形成学科逻辑和生活逻辑的双螺旋互动。

1.自主提问：寻找数学知识与生活经验的结合点

新课标指出：“能够在实际情境中发现和提出有意义的数学问题，进行数学探究。”运用主线问题创意呈现知识是学科逻辑与生活逻辑进行融合的前提。如教学苏教版五下《圆的认识》一课，教师出示汽车车轮、窨井盖、篮球场等图片，引导学生提出“为什么车轮都做成圆形的”“圆形的窨井盖为什么掉不下去”“篮球场中间的圆是怎样画出来的”“篮球运动员围着圆的一圈争球公平吗”“圆有棱角吗”“圆的大小与什么有关”等问题，学生基于生活经验提出的这一系列问题正好直指数学知识的本质，体现了学科逻辑与生活经验的结合点。

2.系统理问：匹配问题结构与生活贯通的联结点

系统理问即根据“是什么—为什么—怎么样”的思路设计主线问题，这样可以形成结构化的数学知识，与对应的生活原型贯通。如教学苏教版六上《认识比》一课，学生提出了许多问题：什么是黄金比？国旗长和宽的比都是3∶2吗？足球比赛中的2∶0 是比吗？有了除法和分数，为什么还要学习比？金龙鱼调和油广告中的1∶1∶1 是什么意义？比有单位吗？……教师围绕学生提出的问题进行整理、排序、细化，提炼出了本节课的主线问题，把“什么是比”作为本节课的核心问题，把“为什么要学比”和“比的应用有哪些”作为探究性问题，另外还设计了一些推进教学的引导性问题。

3.互动追问：观照学科本质与生活共情的锚桩点

提问是问题解决之初的问题，是初始问题；追问是问题解决过程中或之后进一步提出的问题，是后续问题，提问与追问都是主动思考的外显行为。如教学苏教版四下《认识三角形》一课，教师展开了多次追问，如追问“三角形是什么”可以得其表意，索其本意；追问“为什么设计成三角形”，可以知其然，并究其所以然；追问“怎样画三角形的高”，可以懂其原理，学其应用；追问“三角形大小与什么有关”，可以观其现状，思其变化；追问“三角形有什么特性”，可以追根究底，溯其源头。儿童的数学学习就是在“自主提问”和“互相追问”中循环往复，以问题的形式优化认知结构，提升学习能力与思维品质。

三、主线问题的教学样态与实施

双螺旋互动的主线问题教学，其实质是发现和理解学生，关注学生学习方式的改善，引导学生的学习由被动走向主动，由模仿走向创造，全面激发学生的潜能。主线问题教学通过“目标引学—活动导学—评价促学”的模式展开，可以把隐蔽的儿童观、知识观、教育观用主线问题的形式呈现出来，追求基于学生真实问题的自然状态下的数学学习。

1.目标引学——目标问题化

目标问题化是指运用问题的形式呈现目标，以一系列类型丰富、质量优良的问题贯穿整个教学过程，让学生分析、探究、解决问题，从而促进学生提升问题解决能力，发展核心素养。

如教学《认识三角形》一课，课始，让学生找出生活中的三角形，然后提问：关于三角形，你想研究三角形的哪些问题？学生提出了这样几个问题：三角形有什么特点？什么样的图形是三角形？ 桥上的三角形斜拉绳索有什么作用？为什么房顶设计成三角形？怎样画三角形的高？三个点一定能画一个三角形吗？……教师根据学生提出的问题确定了三个目标：（1）通过画三角形，用自己的语言概括什么样的图形是三角形；（2）通过围三角形，认识三角形的高，并知道怎样画三角形的高；（3）通过摆三角形，了解三角形有什么特性和应用。在这里，同一个目标可以通过几个子问题的推进循序渐进地实现，不同的目标也可以通过一个核心问题的推进整合性地实现。

2.活动导学——问题活动化

问题活动化就是把主线问题中的一个或几个问题设计成数学活动，目标监控活动，活动引导目标达成。教学《认识三角形》时，教师设计了三个活动——画一画、围一围和摆一摆，以此来展开相应的探究，激发了学生的学习热情和学习潜力，使他们建立起了结构化的知识结构，培养了批判性思维能力。

（1）激活经验：画一画

学生头脑中已经有了三角形的样子，并画出了自己心目中的三角形。（如图2）这体现出学生不同的学习起点。学生可以直观地说出三角形的边、角和顶点，但在概括“什么是三角形”时有点困难，他们在课堂交流中逐渐理解了三角形的特征，特别是当一个学生用“三条线段的首尾相连”来解释三角形有三条边、三个角、三个顶点时，就表明他将不同思路关联起来了。

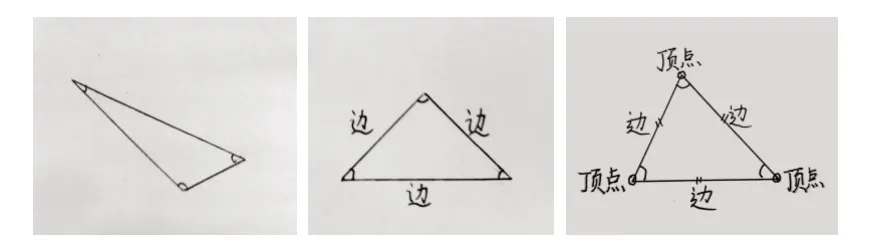
（图2）

（2）打开思维：围一围

理解三角形的高对学生来说是个难点，教师通过改编“试一试”，让学生体会三角形三个顶点的位置确定了，它的形状就固定不变了。如果有一个顶点在不断变高，三角形的形状也不断发生变化，三角形的高也不断增高，学生头脑里高的那条垂直线段呼之欲出，学生自然而然就能把表示高的那条线段画出来，学生对高的表象的建立和意义的理解也就水到渠成了。

（3）体验特性：摆一摆

认识了三角形的特征和三角形的高，有些学生能感受到三角形不易变形，但有些学生还不太清楚三角形的特性。因此，他们通过摆一摆，再通过拉一拉三角形和四边形，感受到三角形不易变形，具有稳定性。此时，三角形的特点和特性便深深刻在了学生的脑海里。

3.评价促学——思维进阶化

儿童的学习是一个不断进阶、不断积累、不断发展的过程。美国教育心理学家布鲁姆将认知学习目标划分为六个层次，从低到高依次为：记忆、理解、应用、分析、综合、评价。人们通常认为前三个层次属于低阶思维，后三个层次属于高阶思维。在《认识三角形》一课的教学中，提出、分析和解决问题的过程就是从低阶思维走向高阶思维的过程。教师要注意根据学生在不同活动中的表现来评价他们的学业水平，促进学生的思维进阶，培养学生的“四能”，提升其核心素养。

总之，双螺旋互动的主线问题教学是一种指向素养生长，培养学生“四能”的教学新样态；是一种以学生的现实水平为起点，以其未来的可能发展水平为方向的教学；是一种学科逻辑和生活逻辑围绕学习逻辑螺旋上升，促进学生思维进阶的教学。