例析中考题中的图形旋转问题

福建省浦城县盘亭中学 (353414) 孙红辉

在2021最新版课标中,图形变化是新课标重要内容,贯穿着整个初中阶段,近几年中考题,甚至压轴题也是频繁出现.从考题中看,对学生的空间思维要求较高,需要学生有一定的空间意识,以及能够通过点、线、图形的旋转进行推理,并通过辅助线找出其中等量关系.这就需要我们老师在平时的教学中,能够让学生在探究学习中具有发现问题,解决问题的能力.本文例举二道中考真题予以说明.

例1 (2022年苏州中考题)如图1,点A的坐标为(0,2),点B是x轴正半轴上的一点,将线段AB绕点A按逆时针方向旋转60度得到线段AC.若点C的坐标为(m,3),则m的值为( ).

图1

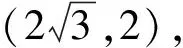
图2

解法2：(构造相似三角形)如图3,在AB线段取中点E,过点E作x轴的平行线分别交y轴、CG于点D、F,∵∠ADE=∠CFE,∠DAE=∠CEF,

图3

∴ΔADE∽ΔCEF,

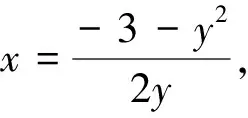
图4

图5

例2 (2021年苏州中考题)如图6,射线OM、ON互相垂直,OA=8,点B位于射线OM的上方,且在线段OA的垂直平分线l上,连接AB,AB=5,将线段AB绕点O按逆时针方向旋转得到对应线段A′B′,若点B′恰好落在射线ON上,则点A′到射线ON的距离d=.

图6

分析：此题为线段绕点旋转,主要考查学生抓住不变量转化的数学思想方法,需要学生有较强的逻辑推理能力.本题由于直线AB是绕直线外点O旋转,不便于抓住图形旋转性质.如连接OB、OA′,可转化为△OAB绕不动点O旋转得ΔOA′B′,抽象的旋转变得更直接.更容易发现问题、解决问题.根据旋转的性质我们可得ΔOAB≅ΔOA′B′,求点A′到射线ON的距离d,或转化成求ΔOA′B′的高,可用等面积等方法求d的值.

图7

图8

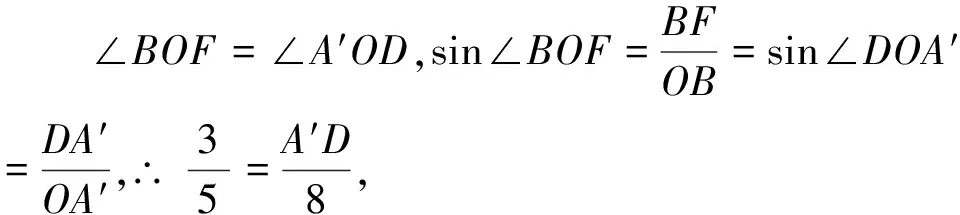
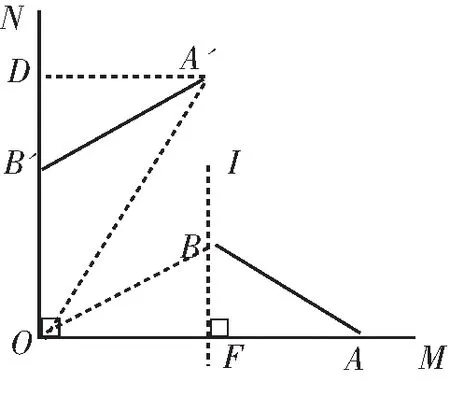
图10

以上二题属图形旋转问题,此题型考察了学生对理论知识的应用,一般地,只有掌握相应的关系式,才可正确、迅速解题.图形变化问题,只有学生掌握相应的规律,做到举一反三,才可理解题意,从而更好的开展解题.初中阶段涉及到的图形平移、轴对称、旋转等图形变换往往都与坐标平面内的坐标变化规律问题相关.教学中应就此类题归纳并作深度分析,只有这样才有助于学生厘清知识的脉络,巩固知识结构.