优化解题策略 促进“四基”落实——以“数列的单调性与最大(小)项”复习课为例

江苏省宜兴第一中学 (214000) 胡志杰

数学知识是丰富多彩的,解题方法是多种多样的,对于同一问题,思考的角度不同其解题方法也会有所不同.那么如何引导学生掌握这些多种多样的方法,并能灵活选择最佳的方法解决问题呢?为了解决这一问题,不少教师选择了“题海战术”,以期通过“多讲多练”帮助学生积累解题方法和解题经验.不可否认,“题海战术”有助于解题经验的积累和解题技能的提升,但是过多地追求数量势必会占用学生思考、归纳总结的时间,不利于知识、经验和方法的内化,影响学生学习能力的提升.因此,在实际教学中,教师应在解题的质量上下功夫,要把知识讲透,方法理顺,切实提高学生解题能力.本文结合“数列的单调性与最大(小)项”复习课,谈谈对优化解题策略的几点认识.

一、关注通性通法,领悟思想方法

数学思想属于思维的范畴,是解决数学问题的灵魂.数学方法是数学思想的具体体现,是解题的重要工具.在解题过程中,只有准确掌握数学思想方法,在解题时才能得心应手.数学思想方法蕴含在数学知识发生、发展和应用的过程中,它不是靠灌输来达成的,需要日常教学中渗透、提炼和感悟.在数学课堂教学中,教师要改变“重结果、轻过程”、“重技巧、轻通法”的错误意识,着重培养和提高学生合理、正确应用数学思想和数学方法解决问题的能力,提升学生数学素养.

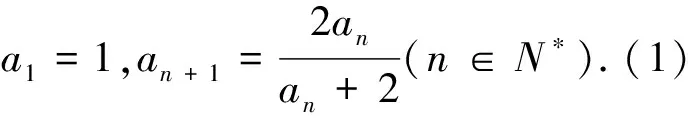
例1难度不大,这样借助学生熟悉的、简单的题目可以引导学生回顾常见的求数列通项公式、判断数列单调性的方法,以此达到巩固“双基”的目的.在解题过程中,教师鼓励学生对不同方法进行对比分析,以便深化对不同方法的理解,找到最佳的解题方法,提高解题效率.

该题具有一定难度,解题时教师可以提供机会让学生合作交流,让学生在议一议、辩一辩中寻找解题的突破口.问题解决后,教师可以引导学生回头看,让学生知晓在应用作差法研究数列的单调性时,需要注意项数的变化,这样通过有效的归纳总结既可以促进数学方法的掌握,又能培养思维的严谨性,促进学生分析和解决问题能力的提升.

在数学教学中,教师不要急于呈现解题过程,应预留时间让学生去思考、去探索,指导学生在问题的解决过程中提炼数学思想方法,以此通过多角度、全方位探究让学生掌握解题的通法,理解问题的本质,以此达到会一题通一类的效果,提高教学有效性.

二、研究多种解法,实现融会贯通

在数学教学过程中,教师应引导学生从不同角度观察、联想、对比,探寻不同的解决方法,以此激发学生数学学习兴趣,发散学生数学思维,增强学生解题信心.

例2 已知数列{an},an=n2+λn+3(其中λ为常实数),若数列{an}为单调递增函数,求实数λ的取值范围.

数学知识之间是相互联系的,教师应鼓励学生应用不同方法解决问题,以此将散落于不同章节的知识有效地串联起来,以此实现知识的融会贯通,提高学生数学应用能力.

三、坚持以生为主,提升探究能力

学生是课堂的主体,在课堂教学中,教师要充分发挥学生的主观能动性,引导学生主动参与课堂教学活动,以此通过亲身参与提高学生认识问题的能力.同时,在课堂教学中,教师要给学生营造一个平等的、和谐的探究环境,让学生亲历知识形成和发展的过程,体验分析和解决问题的思考过程,让学生掌握探索数学知识的方法,发展学生数学核心素养.另外,在教学过程中,教师要为学生提供动手实践的机会和自主探究的时间,鼓励学生提出自己的想法,表达自己独特的见解,帮助学生树立正确的学习观.

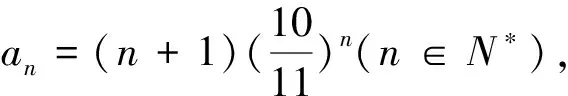
题目给出后,教师让学生认真审题,并思考解决该问题可能用到哪种方法?有的学生认为可以利用数列单调性的定义,有的学生可以认为利用函数的单调性,教师鼓励学生尝试应用不用方法求解,然后对比分析不同方法的优劣,找到适合自己的最佳方法.问题解决后,教师又给出如下变式题目让学生体验、感悟.

变式已知数列{an}的通项公式为an=n2-21n+20.(1)当n为何值时,an有最小值;(2)当n为何值时,数列{an}的前n项和最小.

这样通过适度的变式练习,帮助学生进一步强化已有知识和已有经验,并将其逐渐内化为自身的学习能力,提高学生灵活应用数学思想和数学方法解决问题的能力.

四、重视回顾反思,提高数学素养

在数学教学中,经常会出现“懂而不会”、“一错再错”等现象,出现以上现象的一个重要原因就是缺少解后反思.问题解决以后,教师应鼓励学生回头看,对解题过程、方法、思想进行分析,引导学生对同一类型问题的解法进行归纳概括,并提炼基本思想和方法,并转化为分析和解决问题的工具.

例4 已知数列{an}的通项公式为an=n2+λn+3(其中λ为常实数),若该数列有最小项,且最小项为a3,求实数λ的取值范围.

解题前,教师先引导学生回顾解决此类问题的方法,然后结合题目结构特征分析最佳解题思路.在此过程中,教师重视呈现学生的思考过程,通过互动交流帮助学生深化此类问题的理解.

生1:数列是特殊的函数,在解决最大项或最小项的问题时,可以借助处理函数最值的方法来解决.对于例4,结合已知易得an≥a3对任意n∈N*恒成立,即-7≤λ≤-5.

师:很好,对于以上两种方法,还有什么想说的吗?

这样通过典型练习引导学生对解题方法进行归纳总结,让学生学懂、学透,形成自己的选择,以此有效避免“一错再错”等情况的发生,切实提高解题效率.总之,在复习教学中,教师要控制好题目的数量,加强知识的复习和基本技能的训练,善于通过典型练习帮助学生积累解题经验,提炼数学思想方法,以此促进“四基”的落实,提高学生综合学力.