教材探源 感悟思想 积累经验*——一道函数零点问题的寻根之旅

北京师范大学淮安学校 (223001) 杨兴刚

判断函数零点个数和已知零点个数求参数范围是高考的常考题型.试题多数基于数学情境命制,考查学生灵活运用函数、导数等知识解决问题的能力,全面综合展现极限思想、估算思想的应用和学生的数学素养水平.判断函数零点是否存在不仅要借助函数增长差异的“形”去判断,而且要借助放缩估算的“数”去证明.本文以一道模拟试题为例,通过挖掘教材找根源、一题多解悟方法、反思提升育素养三个维度,探索函数零点问题的寻根之旅.

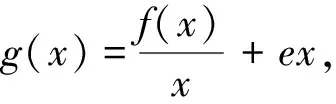
试题根据核心素养的三个水平设计问题,第(1)问通过指数函数考查学生利用导数研究函数单调性的通性通法,属于水平一的要求;第(2)问(ⅰ)由函数零点个数求参数范围考查学生解决一类问题的数学方法,属于水平二的要求; 第(2)(ⅱ)问以不等式放缩和极值点偏移为背景考查学生创造性解决问题的能力,属于水平三的要求,具有很好的区分度.本文重点探索第(2)问(ⅰ)的思维历程,呈现函数零点问题的寻根之旅.

1 教材探源,深化理解

教材中的内容、例题、习题、旁白等都是高考命题的素材,对教材深度理解与挖掘运用是培养学生数学核心素养的根本.教材探源是回归基础、提升能力、发展素养的必经之路.

1.1 直观感受函数变化差异

人教版必修第一册P136第4.4.3节借助信息技术讨论了不同函数:指数函数y=ax(a>1)、一次函数y=kx(k>0)和对数函数y=logax(a>1)图象的增长差异,让学生初步理解“对数增长”、“直线上升”、“指数爆炸”的含义.高一的教学要求主要是让学生直观地感受不同函数的增长差异,不给出严格的证明.在教学过程中,教师可以让学生观察三个函数图象的交点个数,为下节函数零点做好铺垫.

1.2 导数研究函数变化快慢

人教版教材选择性必修第二册P88探究和P89例4,借助导数绝对值的大小,比较了两个函数图象变化的快慢.在教学过程中,教师要借助导数精细研究函数图象的“陡峭”与“平缓”程度,为估算函数值的大小奠定基础.

1.3 泰勒展式估算逼近

人教版教材必修第一册P256拓展探索T26和苏教版教材必修第一册P209阅读题T20均介绍了计算器如何确保计算结果的精确性问题.材料介绍了计算器的工作原理,体会泰勒展式中多项式函数逼近指数函数的估算思想,激发学生深入学习的兴趣,激励学有余力的学生去查阅文献资料,攀登更加美妙的数学大厦.

2 解题探索,感悟思想

通过对问题的多角度思考、分析与对比,不仅可以加深对基础知识、基本技能的理解,而且可以感受基本思想方法的内涵,加深基本经验的积累,促进数学核心素养的发展.

2.1 极限思想下的解法

评注：上述分离参数法,强调了指数式可以通过两边取对数实现参数分离,借助函数变化差异和极限思想辅助说明图象函数的焦点个数,体现了数形结合的直观表达.

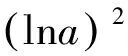
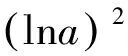
2.2 估算解法

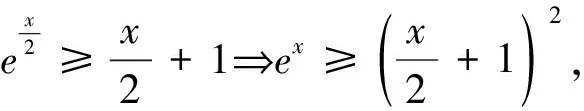
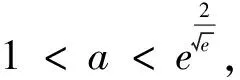
评注：本解法很好的回避了极限思想的应用,更加贴合高中教学实际和高考函数零点问题的标准解答,并且给出了如何利用切线不等式构造二次函数探索零点区间值的取法问题.

3 反思积累经验

数学高阶思维是数学核心素养的重要组成部分.高阶思维是个体适应环境、寻找认知平衡的关键能力.[2]对复杂情境的问题的解决,不仅需要学生自己有扎实的基本活动经验积累,而且需要学生之间的展示与交流、质疑与表达.学生要积极参与数学活动,在问题的分析与解决过程中,碰撞出新的思维火花,在批判质疑的交流活动中,理解数学知识本质,深化数学方法理解,搭建拾级而上的思维桥梁,感悟数学思想方法的魅力.