不规则凸区域的水面舰艇最短搜潜航路自动规划

周寅飞, 张立华,2*, 贾帅东,2, 戴泽源, 刘翔

(1.海军大连舰艇学院 军事海洋与测绘系, 辽宁 大连 116018;2.海军大连舰艇学院 海洋测绘工程军队重点实验室, 辽宁 大连 116018)

0 引言

水面舰艇具备良好的对潜探测和遂行打击能力,是重要的反潜兵力[1]。区域搜潜是水面舰艇所担负的搜潜任务之一,是指在一定时间和范围内,为保护海军港口、舰艇编队等目标不受敌方潜艇攻击所进行的作战活动[2-3]。

搜潜航路规划是水面舰艇进行区域搜潜前需要进行的基础性工作[4],其规划目标是在最短时间内完成对搜潜区域的全覆盖搜索[5]。敌方潜艇力量一般在开阔海域出没,为便于检查搜潜的分析和实施,一般只考虑在开阔海域的规则矩形区域搜潜这种简单情形,如图1所示,并主要采用平行线式的航路进行搜潜[5]。针对这种简单情形,众多学者结合声呐的使用特性与搜索论,对搜潜航路布设的改进方法进行了诸多探索[6-10]。

随着近年来海上形势的逐渐加剧,不明潜艇力量出没重要海峡、重要港口等复杂海域的次数急剧增多,面临的水下威胁陡然增大,而规则矩形搜潜区难以对海峡、港口形成有效封锁。因此,研究不规则区域的检查搜潜,成为了一种急切的现实需求。

目前国内外关于水面舰艇在不规则区域搜潜的航路自动规划研究还相对较少,但不规则区域的无人测量船覆盖路径规划研究已经取得了较为丰硕的成果。当前无人测量船覆盖路径规划算法可主要分为两类:

1)经典算法。Pang等[11]采用随机游走方法实现了区域覆盖路径规划,并对搜索效率进行了定量计算;基于混沌运动原理,Sridharan等[12]规划路径实现了对作业区域的高效率覆盖;Dong等[13]提出一种加权的生成树算法来生成覆盖扫描路径,确保了搜索效率和算法鲁棒性;Khan等[14]结合经典的Boustrophedon方法,建立起覆盖路径规划的优化回溯机制,原理清晰且规划效果较好。

2)启发式算法。为实现无人船在水质检测点间的自主巡逻,Zhang等[15]提出一种改进遗传算法来实现全覆盖路径规划;赵红等[16]对原生物激励神经网络算法进行改进,有效实现了对无人船区域覆盖路径规划;Xiong等[17]通过Voronoi图划分搜索区,然后使用改进蚁群优化算法进行无人船的覆盖路径规划。

以上算法可基本实现对不规则复杂区域的覆盖路径规划,但是,无人测量船测量作业与水面舰艇搜潜活动存在一定的区别:1)无人船转向半径较小且易于转向,而水面舰艇转向半径较大且不易于转向;2)无人船转向对测量设备工作影响较小,而水面舰艇转向会对声呐正常工作造成较大影响;3)无人船测量工作区域一般为沿岸或岛礁区,外部轮廓较为复杂,而在搜潜任务中的不规则搜潜区域大多情况下可以设定或分割为不规则凸区域。因此,其算法规划出的路径与水面舰艇搜潜需求存在不相配适的问题。无人测量船覆盖路径规划算法很少顾及船舶转向代价,并且由于该类算法主要关注于对不规则区域的分割和多区域间的遍历,故针对凸区域规划出的路径可能并非最优路径。

综上所述,如何综合考虑水面舰艇转向代价、为水面舰艇在不规则凸区域搜潜规划出一条最短搜潜航路,尚且没有针对性研究。

本文针对不规则凸区域的特殊性,分析论证搜潜航路总长度与转向次数的线性关系,挖掘最优搜潜航向与不规则凸区域边界的内在关联规律,设计最优搜潜航向的求取算法,提出最短搜潜航路自动规划方法。

1 不规则凸区域的水面舰艇最短搜潜航路自动规划

1.1 最短区域搜潜航路的长度计算模型

1.1.1 区域搜潜航路的构成

水面舰艇进行搜潜的示意图如图2所示,w为声呐的有效探测宽度。由图2可以看出,搜潜航路由有效搜潜航路(长度为Le)和转向调整航线(长度为Lt)两部分组成,且航线总长度L为

L=Le+Lt

(1)

图2 水面舰艇搜潜示意图Fig.2 Schematic diagram of surface warship submarine search

1.1.2 有效搜潜航路的长度求解

舰船在转向调整过程中搜潜能力较弱。水面舰艇搜潜主要使用舰壳声呐和拖曳声呐等主被动搜潜设备,利用声波对水下目标进行探测。然而,很多干扰因素都会对声呐正常工作造成影响,舰艇的转向就是其中之一[18-19]。舰艇大幅转向产生的自噪声会严重影响舰壳声呐的目标识别与定位;且转向时会造成拖曳声呐阵列的阵型畸变,对拖曳声呐探测能力产生较大的衰弱[20-21]。水面舰艇的转向半径也相对较大,使得转向的时间较长,而声呐在该过程中持续地受到干扰,会严重削弱舰艇的搜潜能力。因为转向对搜潜带来了诸多的不良影响,故在进行区域搜潜的过程中,转向调整航线不计入有效搜潜航路。

根据区域搜潜的战术目标要求,水面舰艇的有效搜潜航路应实现对搜潜区域的全覆盖搜索。故设搜潜区域面积为S,有

S=Lew

(2)

则可得

(3)

对于一个确定的搜潜区域,其搜索面积S为定值;对于某型声呐而言,其有效探测宽度w也可以视为定值。由此可以推断出:在一个确定的区域内,无论以怎样的方式进行搜潜,其有效搜潜航路的长度Le是一定的。

1.1.3 转向调整航线的长度求解

由式(1)可知,航线总长度L为有效搜潜航路长度Le和转向调整航线长度Lt之和,由式(3)可知,有效搜潜航路的长度Le为定值,则可以推导出:在不规则凸区域内,检查搜潜的最短航线为转向调整航线长度Lt最小的航线。

在搜潜过程中,转向调整航线是为了指引舰船进行转向调整,因此转向调整航线的长度Lt与转向次数x具有线性关系:

Lt=ltx

(4)

式中:lt为每次的转向代价。可由式(4)推导出,若使转向次数x最小,即可使转向调整航线长度Lt最短,进而使搜潜航路总长度L最短。

为求取总的转向调整航线长度Lt,在转向次数x确定后,需求解每次转向的代价lt。舰船在转向过程中会降速而导致航行时间增加,可以将增加的时间转换为等效航程,并作为转向代价。转向半径相对与声呐有效作用范围而言较大,在现有声呐装备条件下,难以进行忽略,且是计算转向代价的重要参数。根据文献[22],定常回转阶段舰船的航速v与直航航速v0之比为

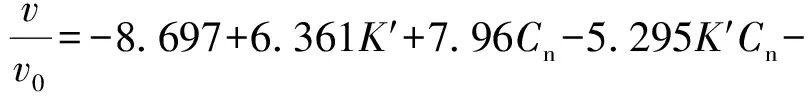
(5)

式中:K′为旋回性指数;Cn为舵的法向力系数;θ为转向角。进而可根据文献[23-24],求得转向代价:

(6)

式中:R为转向半径。

1.1.4 最短搜潜航路的长度计算模型

综合式(1)、式(4),可得

L=Le+ltx

(7)

由式(3)已经证明得到,在同一个区域内,有效搜潜航路Le是定值,因此,可由式(7)证明得到航线总长度L与转向次数x存在线性关系,可进一步得到最短搜潜航路Lmin的数学模型:

Lmin=Le+ltxmin

(8)

式中:xmin为最小转向次数。

由式(8)可知,转向次数最少可使搜潜航路总长度最短,且转向次数最少的航向为最优搜潜航向。

1.2 最优搜潜航向的求解算法

1.2.1 搜潜航向确定的转向次数求取

对一个固定的搜潜区域而言,假设搜潜航向确定,该区域可与搜潜航向平行的两条直线相切,如图3 所示。设两平行直线的垂直距离ds为搜潜带整体的宽度,则该航向对应的转向次数x为

x=ds/w

(9)

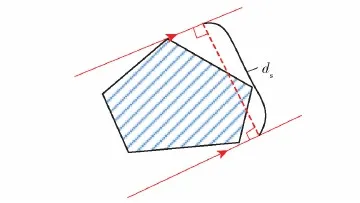
图3 搜潜带示意图Fig.3 Diagram of the search zone

水面舰艇的声呐有效作用距离在战术问题研究中根据可设为常数,声呐的有效探测宽度w也可根据声呐参数设置为常数。因此可以从式(9)推导出,若想转向次数最小,则需选择合理的航线方向,使得在该航向上,搜潜带整体的宽度ds最窄。

1.2.2 具有最少转向次数的搜潜航向选取

在区域搜潜任务中,搜潜带需实现对搜潜区域的全覆盖,则可从图3看出,对于一个凸区域,搜潜带边界必过凸区域的某顶点。在经过某顶点的搜潜带中,搜潜航向与凸区域边界平行时宽度最窄,分析论证如下:

1)过指定点做任意方向的搜潜带和与凸区域边界平行的搜潜带。其基本步骤为:首先,在最优搜潜航路方向选取示意图(见图4)中,设定搜潜凸区域;然后在凸区域上做一个任意方向搜索带,并将其逆时针旋转至与凸区域边平行,如图4(a)所示;最后,在凸区域上做一个任意方向搜索带,并将其顺时针旋转至与凸区域边平行,如图4(b)所示。过凸区域顶点P4做一个任意方向(设该方向为方向1)的搜潜带,如图4(a)、图4(b)所示。在图4(a)中,该搜潜带逆时针旋转直至与直线P1P2平行,如图4(a)所示,设该方向为方向2,可以看出,P4是凸多边形顶点中离直线P1P2垂直距离最远的点;在图4(b)中,搜潜带顺时针旋转直至与直线P3P4平行,如图4(b)所示,设该方向为方向3,可以看出,P1是凸多边形中离直线P4P3垂直距离最远的点。

2)搜潜带宽度的比较。在图4(a)中,过P4向两条搜潜带分别做垂线,可以得到方向1搜潜带的宽度为P4V2,其与凸区域边界P1P2相交于点V2,方向2搜潜带的宽度为P4V1;在图4(b)中,过P1向两条搜潜带分别做垂线,可以得到方向1搜潜带的宽度为P1I2,其与凸区域边界PaP4相交于点I1,方向3搜潜带的宽度为P1I3。由图4(a)三角形P4V1V3、图4(b)三角形P1IaI1斜边和直角边的长度关系,可得

(10)

图4 最优搜潜航路方向选取示意图Fig.4 Schematic diagram of optimal search route direction selection

由式(10)可知,方向1搜潜带的宽度比方向2、方向3搜潜带的宽度都要长。

通过上述证明过程可得,最窄搜潜带必然与凸区域的某条边平行。

根据此结论,可通过以下步骤找到最窄搜潜带,进而得到搜潜带所对应的最优搜潜航向:

步骤1以凸区域边P1P2作为起始遍历边,比较各顶点到P1P2的垂直距离,因搜潜带需实现对区域的全覆盖,故需找到距离边P1P2最远的顶点P4。

步骤2记录P4到边P1P2的垂直距离,作为边P1P2所对应的最窄搜潜带宽度。

步骤3遍历凸区域的所有边,重复步骤1～步骤3,直至完成对凸区域所有边的遍历。

步骤4比较各边所对应的最窄搜潜带宽度,在其中选择最窄的作为凸区域整体的最窄搜潜带宽度,整体最窄搜潜带对应的边的方向为最优搜潜航路方向。

1.3 最短搜潜航路自动规划的实现

在1.1节中,证明了转向次数最少可使搜潜航路总长度最短,且转向次数最少的航向为最优搜潜航向;在1.2.1节中,提出最优搜潜航向的求解算法。在此基础上,基于贪婪思想,进一步实现最短搜潜航路的自动规划。

1.3.1 基于空间拓扑方法求解有效搜潜航路

最优搜潜方向是有效搜潜航路的方向,因此可沿1.2节算法求得的最优搜潜航路方向,以搜潜带宽度w为间隔做直线,如图5(a)所示,可用搜潜区域对所生成直线进行拓扑裁剪运算,得到区域内的有效搜潜航路P1P2、P3P4、P5P6、P7P8。

图5 基于优化算法的最短搜潜航路自动生成示意图Fig.5 Automatic generation schematic diagram of shortest underwater searching route based on optimization algorithm

1.3.2 基于贪婪思想的航线自动生成

基于贪婪思想的自动生成方法主要分为4步:

1)搜索得到离水面舰艇所在位置距离最近的搜潜航路上的点,作为搜潜起始点;

2)计算得到各搜潜航路点Pi、Pj两两间的距离lij,生成航路点距离表,如表1所示;

3)为使得后续算法能够优先遍历未通过的有效搜潜航路,在此人为设定有效搜潜航路的距离为虚拟值0;

4)基于贪婪思想进行最短搜潜航路的自动生成,即不断搜索距离当前航路点最近且未遍历过的航路点,作为下一个航行的航路点,并且将遍历过的航路点设置为不可搜索的航路点,直至遍历完所有的搜潜航路点。

具体过程为:首先,从起点位置P2出发搜寻距离最近的点,由表1得知,P1点与P2的距离为0 m,因此选择接下来通过P1P2到达P1位置,如图5(c)所示,并将P1、P2点设置为不可搜索的点;然后,从P1点出发,搜寻得到未通过且距离最近的航路点P3,如图5(d)所示;随后从P3出发,由表1得知P3点与P4的距离为0 m,则选择通过P3P4到达P4位置,如图5(e)所示,并将P3、P4设置为不可搜索的点。不断按上述过程进行航线生成,直至完成对所有搜潜航路点的遍历,最终得到的最短搜潜航路为图5(f)所示蓝色虚线。

表1 搜潜航路点距离Table 1 Distance between waypoints in submarine search

2 实验与分析

为验证本文所提最短搜潜航路自动规划方法的有效性,在实验1中,分别通过本文方法与经典的Boustrophedon方法[14]生成航路进行对比,以验证本文方法相较于现有方法,更适用于水面舰艇区域搜潜航路的规划;在实验2中,将本文方法生成的搜潜航路,与以1°为最小分割角度遍历得到的搜潜航路进行对比,以验证本文方法规划出的搜潜航路具备全局最优性。

2.1 实验1

本实验选取某海峡附近海域进行实验,假设潜艇可能在30 m以上水深的海域活动,舰艇搜潜的有效搜潜带宽度为500 m,可根据该水道的30 m等深线设定搜潜区域,如图6(a)所示;通过Boustrophedon方法生成的航路如图6(b)所示;通过本文方法生成的搜潜航路如图6(c)所示。两种方法所规划航路的长度、转向次数以及对搜潜区域的覆盖率统计如表2所示。

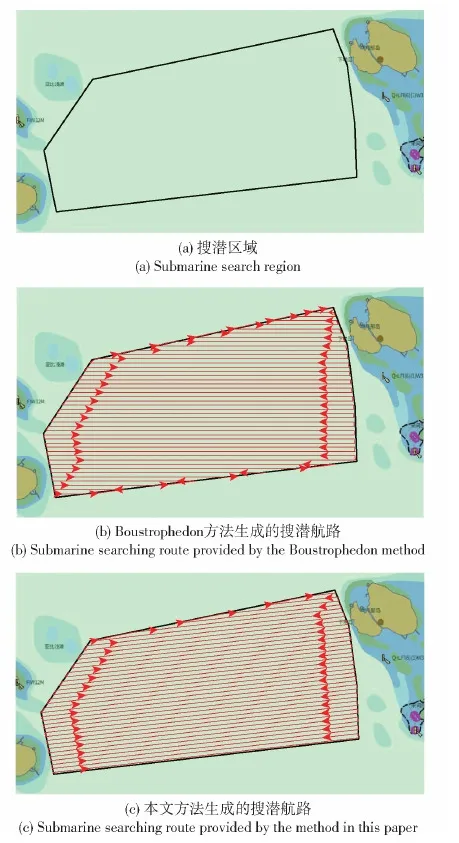
图6 对比方法实验结果示意图Fig.6 Schematic diagram of comparison method results

从图6(b)中可以看到:Boustrophedon方法在凸区域中生成的航线是与坐标轴方向平行的,并不具备顾及不规则凸区域的形状与舰船转向代价,自适应生成最优搜潜航线的功能;本文方法生成的航路能够根据不规则凸区域的具体形状选择最优搜潜航线方向,进而生成最短搜潜航路。从表2对比数据中可以看出,本文方法生成的航路总长度、转向次数比Boustrophedon方法生成的航路更短,且有效覆盖率更高。

2.2 实验2

本实验选取某港附近海域进行实验,进出该港的水道水深基本在35 m以上,潜艇在此坐底后,鱼雷打击范围可覆盖该水道,能够对进出的舰船造成极大威胁。

假设潜艇可能在30 m以上水深的海域活动,舰艇搜潜的有效搜潜带宽度为500 m,可根据水道的30 m等深线,设定搜潜区域如图7(a)所示,通过本文最短搜潜航路自动规划方法生成的搜潜航路如图7(b)所示,所对应的航路总长度、转向次数和对搜潜区域的覆盖率如表3所示。为验证采用本文方法生成的搜潜航路总长度最短,对0°～180°的搜潜航向以1°为最小分割角度遍历得到对比搜潜航路,并将每5°的搜潜航路长度、转向次数以及对搜潜区域的覆盖率统计到表3中。

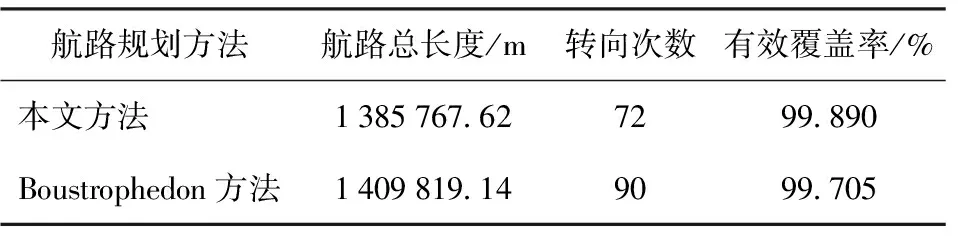
表2 对比方法搜潜航路实验数据统计Table 2 Statistical table of experimental data of comparison methods

从表3的统计数据中可以看出:最短搜潜航路的搜潜航向是60.39°,遍历得到的航路从0°/180°的搜潜方向开始,方向越接近最优搜潜航向,其航线总长度越小;遍历得到的航路从搜潜航向大于60.39°的方向开始,随着与该方向夹角的增大,其航路总长度逐渐增大;搜潜航路总长度与转向次数存在相关性,转向次数越多,搜潜航路总长度越长。

图7 搜潜区域与最优搜潜航路实验结果Fig.7 Experimental results of search area and optimal search route

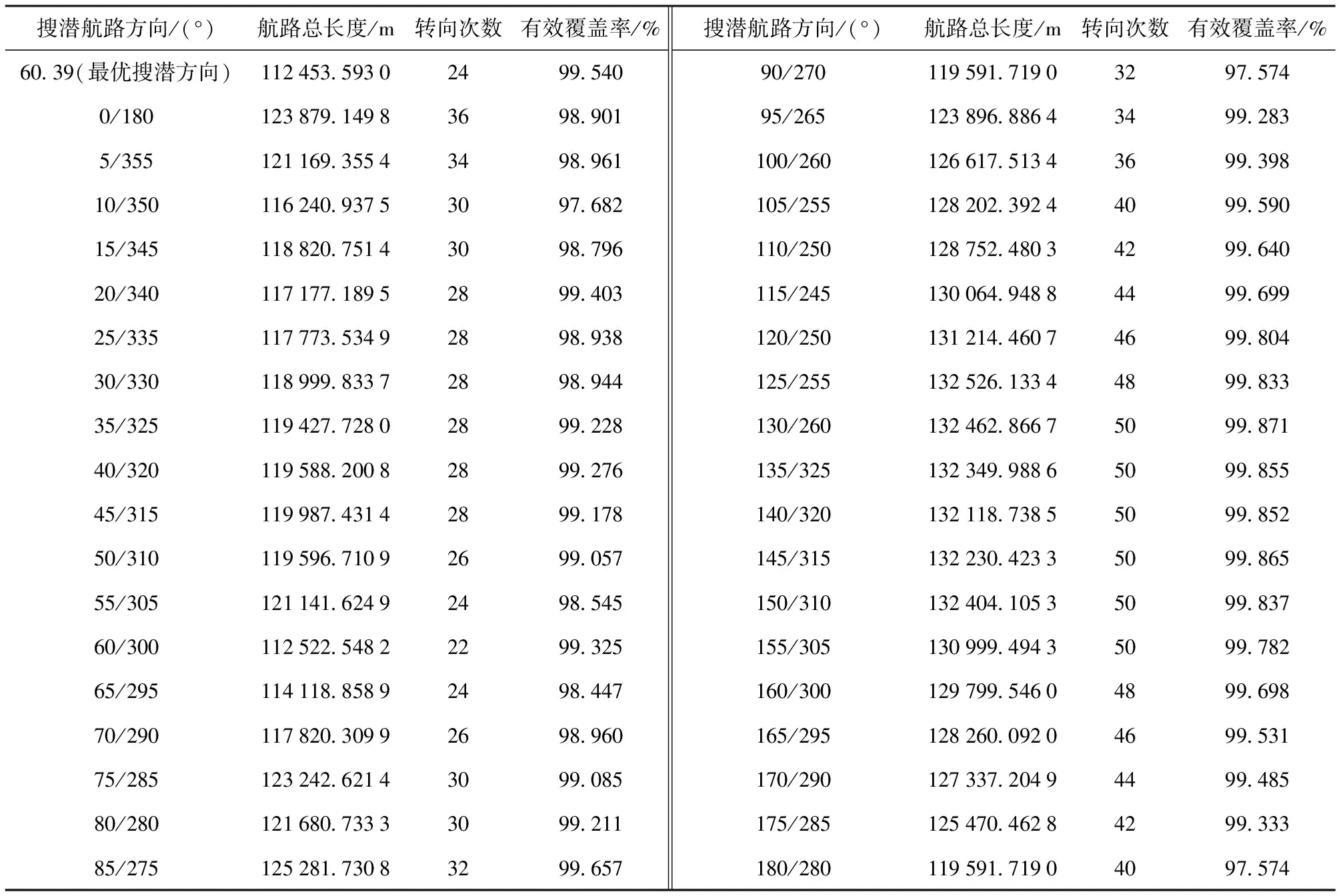
表3 搜潜航路实验数据统计

实验结果表明,通过本文最短搜潜航路自动规划方法求得的搜潜航路具备全局最优性,其搜潜方向是最优搜潜方向,航路总长度最短。同时,从表3中可以看出,搜潜航路对搜潜区域的有效覆盖率基本达到了99.5%以上,能够满足水面舰艇复杂区域检查搜潜应基本不存在盲区的战术要求。

3 结论

本文通过经理论推导和实验对比分析,对不规则凸区域的水面舰艇最短搜潜航路自动规划进行了研究。得出以下主要结论:

1)搜潜航路总长度与转向次数存在线性关系,转向次数最少可使搜潜航路总长度最短,且转向次数最少的航向为最优搜潜航向。

2)最优搜潜航向必然与凸区域的某条边平行,故与凸区域边平行的搜潜航向中,搜潜带总体宽度最窄的即为最优搜潜航向。

3)所提方法规划出的搜潜航路,与通过遍历方法所得到的各搜潜航路相比,总航程最短。

虽然本文方法对区域搜潜实际中最常见的凸区域搜潜最短航线自动生成方法进行了研究,然而如何依据本文证得的结论,在搜潜区域为更复杂凹区域等情况下求解得到全局最优解,还有待于下一步研究。