基于变分正则化参数估计的伪码调相引信重构式干扰方法
彭 博, 陈齐乐, 李 锐
(1.北京理工大学 信息与电子学院, 北京 100081; 2.江苏自动化研究所, 江苏 连云港 222061;3.北京理工雷科电子信息技术有限公司, 北京 100081)
0 引言
无线电引信干扰技术是保护己方作战单位的重要手段,是电子对抗技术的重点研究内容之一[1-2]。目前引信干扰机已从早期预置波形的干扰策略发展为利用数字射频存储(DRFM)[3]截获引信发射信号,并通过转发或者重构引信信号实现相干干扰的策略。其中重构式干扰[4-5]在截获信噪比较低的条件下仍能确保干扰信号同引信信号高度相干,是新一代引信干扰机的重要技术特征。重构式干扰的关键在于低信噪比条件下精确估计信号的调制参数,但以伪码调相信号[6-7]为代表的低截获概率信号给干扰机参数估计带来了极大的困难。
信号参数估计是信号处理的一个重要研究方向,其在无源测向雷达[8]、认知雷达[9]及雷达对抗[10]等领域具有重要意义。其通过多种时频分析方法,如短时傅里叶变换、小波变换[11]、经验模态分解[12]、傅里叶求积变换[13]、全变分正则[14]、迭代滤波[15]等,从噪声中提取接收信号的调制参数。文献[16]利用线性调频(LFM)信号在分数阶域的聚集性,设计了基于分数阶傅里叶变换的调频斜率估计方法。文献[17]针对脉冲噪声设计了基于压缩变换函数的LFM信号参数估计方法。针对伪码调相信号,目前主要采用基于循环谱及高阶相关的方法,这些方法通常需要先验信息,且大部分局限于m序列的估计。文献[18-20]分别提出了基于循环谱密度、2阶循环统计及随机共振的方法,但这些方法仅能够估计信号载波频率和码元速率,无法估计伪码序列。文献[21]提出了基于循环谱密度的伪码序列估计方法,但需已知码元速率和载频。文献[5]利用3阶相关函数估计伪码序列,并获取其本原多项式,进而得到完整序列。但该方法不仅需要已知序列长度,而且仅适用m序列的估计,无法应用于M序列、混沌码序列等伪码序列的参数估计。文献[4]利用Duffing振子的提取信号的伪码序列,但目前混沌系统的工程实现仍是一个难题。伪码序列估计的难点在于传统时频分析方法难以有效提取相位突变,文献[22]提出了一种可以分离接收信号中的分段平稳跳变、低频趋势及高频振荡分量的算法。但伪码调相信号为跳变信号同振荡信号的乘积形式,无法利用该算法直接分离。
针对重构式干扰面临的低截获信噪比条件下伪码调相信号盲参数估计困难,本文提出变分正则化参数估计方法。该方法将伪码调相信号的中心频率估计和伪码序列估计分为两个子问题。首先利用插值傅里叶算法精确估计信号中心频率,并根据估计结果将截获信号下变频为零中频信号;其次提出基于非凸稀疏增强正则项的全变分正则化伪码序列估计方法;根据参数估计结果重构引信信号形成干扰。最后通过仿真和试验验证了本文方法的有效性。
1 无线电引信干扰系统模型
1.1 伪码调相引信信号模型
伪码调相引信通过伪码控制载波相位反转扩展引信工作带宽,利用伪码序列优良的自相关性,在保证定距精度高的同时具有更强的抗干扰性能,其发射信号可表示为
(1)
式中:l为调制周期序列号;K为码元总数;ck为伪码序列,ck={1,-1};rect(·)为表示门函数;t为信号发射时间;k为伪码序列号;Tc为码元宽度;T为调制周期,T=PTc,P为码长;f0为载波频率;φ0为初始相位。
引信接收到目标回波信号,经过全相干解调获得目标的距离和速度信息。传统预置波形干扰同伪码调相引信信号相干性较差,无法干扰引信。而DRFM采用截获并转发或重构引信发射信号的方式,其产生的干扰信号同引信发射信号具有较强的相干性。
1.2 重构式干扰模型
重构式干扰是指DRFM在截获引信信号后,通过信号参数估计及重构实现相干干扰的干扰方法。不失一般性,假设DRFM截获信号时长为一个调制周期,系统AD采样率为fs,则针对伪码调相引信截获信号可表示为
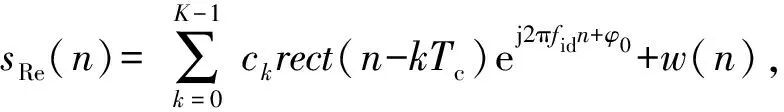
(2)
式中:n为采样点数序列号;fid表示截获信号的中心频率;w(n)为环境;N为总采样点数。
DRFM根据参数估计结果重构形成的干扰信号可表示为
(3)
(4)
式中:S表示延时总数;τs为干扰预设延时。
1.3 信号参数估计模型
在低信噪比的复杂电磁环境下,DRFM截获信号受噪声影响严重,如果采用直接转发的干扰策略则会导致干扰信号同引信信号相干性下降,从而影响干扰效果。重构式干扰通过截获信号参数估计及重构避免截获噪声对干扰效果的影响。重构式干扰的关键在于准确估计截获信号参数,针对伪码调相信号,参数估计模型可表示为
(5)
式(5)为3个未知参数求极值问题,该表达式直接求解难度较大。由于伪码调相信号载波频率同伪码序列为相互独立的两个变量,本文将中心频率和伪码序列分开求解。
2 基于变分正则化参数估计的伪码调相引信信号重构干扰方法
基于变分正则化参数估计的伪码调相引信信号重构干扰方法总体方案如图1所示。伪码调相信号参数估计分为中心频率估计和伪码序列估计两个子模块。中心频率估计子模块利用插值傅里叶算法精确估计截获信号中心频率,并将估计结果给到伪码序列估计模块中;伪码序列估计模块则根据中心频率估计结果将截获信号下变频至零中频信号,并通过变分正则化算法估计调制信号的伪码序列。最后,系统根据参数估计结果重构引信信号形成干扰。

图1 基于变分正则化参数估计信号重构干扰方法原理框图Fig.1 Diagram of the proposed method
2.1 基于插值傅里叶的中心频率估计方法
为精确估计截获信号中心频率,算法首先将I、Q两路采样信号平方后作差,获得不含调相信息的倍频信号,倍频信号可表示为
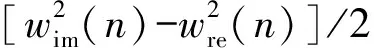
(6)


(7)
式中:W(±0.5)表示噪声频谱。由于根据泰勒级数展开,式(7)可以简化为
(8)
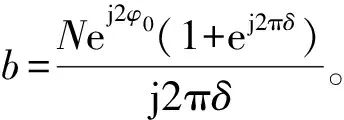
(9)
为提高粗估计误差的估计精度,可以在更新频率估计结果后重复式(7)~式(9)步骤,通常迭代两次即可逼近克拉美罗界。根据估计结果,伪码调相信号中心频率可表示为
(10)

图2 基于插值傅里叶的中心频率估计算法Fig.2 Center frequency estimation algorithm by interpolation on Fourier coefficients
基于插值傅里叶的中心频率估计流程图如图2所示。伪码调相信号初相则可以通过FFT谐波系数获得,若假设倍频信号次谐波系数为X(),则伪码调相信号初相可以表示为
(11)
2.2 基于变分正则化的伪码序列估计算法
根据1.3节,式(5)涉及3个未知量,求解难度较大,这里将各个参数分开求解。根据信号中心频率和初相参数估计结果,对伪码调相信号作正交下变频,获得零中频信号为
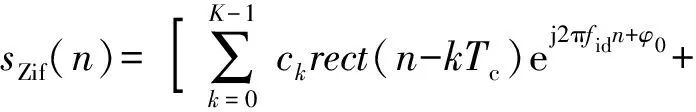
(12)
当中心频率估计结果满足fid=id、φ0=0,则式(12)可化简为
(13)
伪码序列参数估计问题转化为变分去噪问题:
(14)
式中:c为待求解序列。由于上述问题为非正定问题,这里引入拉格朗日惩罚因子确保解的唯一性,采用稀疏增强函数作为惩罚因子建立目标函数:
(15)
式中:D为诺依曼边界条件补偿的1阶差分矩阵;a为非凸度控制参数;λ为正则化参数;φ(·,a)为稀疏增强函数,
(16)
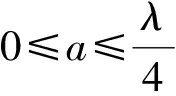
(17)
式(17)为非线性函数,无法直接求解,这里拟采用前后向分裂优化算法求解。令
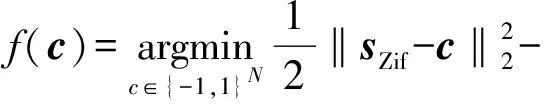
(18)
式中:v为迭代求解中间变量,将具有相关性的变量c和Dc相互分裂。
由于f(c)关于函数c连续,g(c)为关于c的有界凸函数,根据前后向分裂优化算法原理,有
(19)
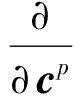
zp=aDT(Dcp-soft1/a(Dcp))
(20)
(21)

式(21)可以通过文献[24]所提方法求解。给定初始状态c=0N,通过多次迭代式(20)和式(21),即可获得伪码调相信号的伪随机码序列。基于全变分正则化伪码序列估计算法如图3所示。
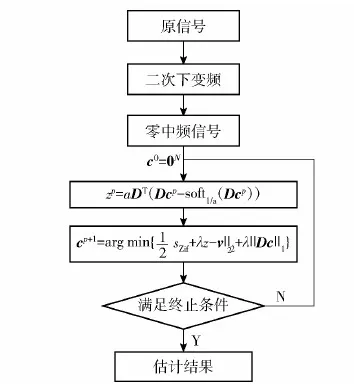
图3 基于全变分正则化的伪码序列估计方法流程图Fig.3 Estimation method ofpseudo codes by total variation regularization
3 参数估计性能及干扰效果分析
3.1 测频精度分析
假设DRFM接收的噪声为零均值、方差为σ2的加性高斯白噪声。根据式(6),倍频信号的噪声可表示为

(22)
式(22)前两项之和仍为零均值、方差为σ2的高斯白噪,最后一项为σ2的高阶无穷小,可以认为倍频信号信噪比同截获信号一致。根据文献[25]可知,中心频率测量方差可表示为
(23)
式中:ρ为截获信噪比。当δ=0时,测频算法具有最小测量方差,约为1.01倍的克拉美罗界。测频算法采用迭代更新的策略,因此经过迭代更新后可以认为算法测频方差为1.01倍克拉美罗界(每次更新后的测频结果都更接近真是频率,即δg+1<δg,g表示迭代次数)。最终可得算法的测频方差可表示为
(24)
3.2 伪码序列估计精度分析
基于变分正则化的伪码序列估计算法主要通过序列阶跃跳变来提取伪码序列。不同于传统的相关检测,该算法码元估计精度完全取决于信号采样率。码元宽度估计误差
(25)
信号中心频率估计误差则会影响伪码极性估计的准确性。不考虑噪声影响时,二次下变频的零中频信号可表示为
(26)
式中:Err(id)=id-fid。零中频信号的1阶差分可表示为
sZif(n)-sZif(n-1)=
j2πδ(k)Err(id)ej2π[Err(id)n+(φ0-0)]
(27)
根据式(27),测频误差会导致伪码序列1阶导数幅值大小以及极性发生变化,从而造成伪码序列的估计错误。当测频误差为3倍标准差时,则
(28)
为准确估计码元宽度,通常信号采样率较高、采样点数N较大。因此式(28)远小于1,即伪码序列时长远小于测频误差周期,在实际工程应用时,测频误差对伪码序列估计准确性的影响相对较小。
3.3 干扰效果分析
根据伪码调相引信原理,干扰信号进入引信接收机经全相干解调输出的多普勒信号可表示为
(29)
式中:τ0为引信预设起爆延时;Rs(·)为伪码估计结果同原始序列的相关函数;fd为弹目项目运动导致的多普勒频率。从式(29)中可知,重构式干扰效果主要受参数估计结果影响,伪码序列估计结果决定干扰信号同引信发射信号相关峰大小,中心频率估计结果则影响引信输出多普勒频率。
4 仿真及实测验证


表1 仿真参数Table 1 Simulation parameters
4.1 仿真验证
在干扰机截获信噪比-10~10 dB的条件下,基于插值傅里叶的中心频率估计结果及误差仿真结果如图4所示。从仿真结果中可以看出,算法具有极高的频率估计精度,在信噪比SNR=10 dB时估计误差小于5 kHz,当SNR下降为-10 dB时估计误差约为20 kHz。采用3倍标准差衡量估计误差,仿真结果如图5所示。从仿真结果中可以看出,在-10 dB时,频率估计的3倍标准差为60 kHz,即算法在SNR>-10 dB的条件下,频率估计误差不超过60 kHz。
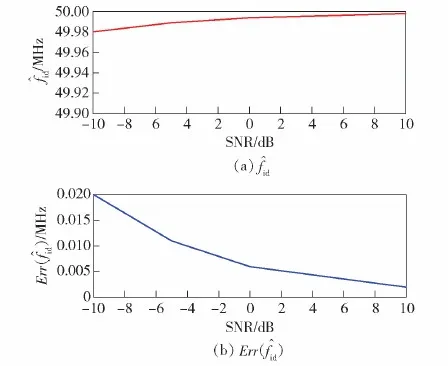
图4 不同信噪比下频率估计仿真结果Fig.4 Estimation results with different SNR values

图5 频率估计的3倍标准差Fig.5 Triple standard deviation of the estimation results
在0 dB信噪比条件下,基于变分正则化伪码序列估计算法中间变量z及估计结果的仿真结果如图6所示。从仿真结果中可以看出,算法通过中间变量z提取序列跳变位置,并根据z的极性确定序列的极性,因此算法具有极高的码元估计精度。
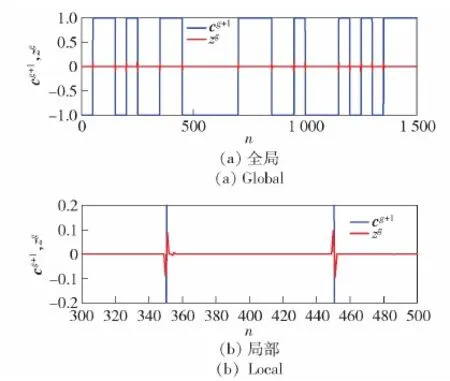
图6 算法中间变量和最终估计结果Fig.6 Intermediate variables and final results
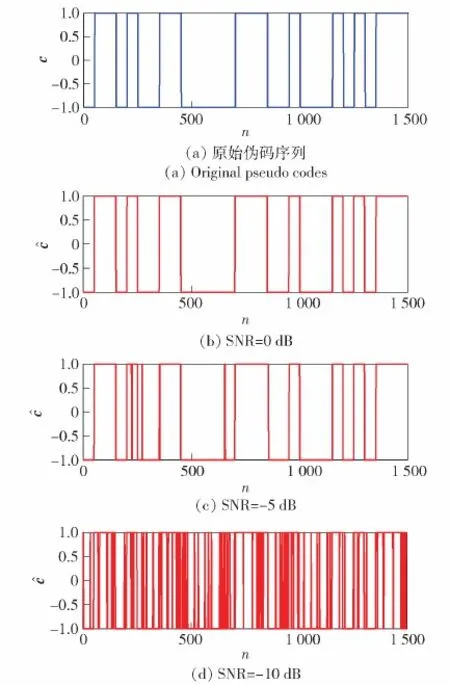
图7 不同信噪比下伪码序列估计结果Fig.7 Estimation of pseudo codes with different SNR values
基于变分正则化的伪码序列估计仿真结果如图7所示,其中图7(a)为原始伪码序列,图7(b)、图7(c)和图7(d)分别为信噪比0 dB、-5 dB及-10 dB条件下伪码序列估计结果。从仿真结果可以看出,当信噪比大于-5 dB时,伪码序列估计结果较为准确,基本同原伪码序列一致。当信噪比为-10 dB时,估计结果受噪声影响较大,同原伪码序列具有一定差异。
为定量分析伪码序列估计结果的准确性,在不同信噪比条件下分别进行了100次蒙特卡洛仿真实验,并计算估计结果同原始伪码序列相关系数的均值。仿真结果如图8所示。从仿真结果可以看出,在信噪比高于-5 dB时,相关系数大于0.90,而当信噪比恶化到-10 dB时,相关系数仍保持在0.72左右。
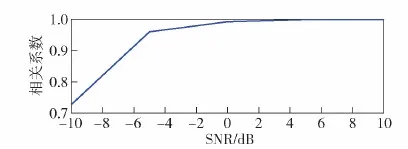
图8 不同信噪比下相关系数仿真结果Fig.8 Correlation coefficients with different SNR values
在环境信噪比为0 dB条件下(包括干扰机截获信噪比和目标回波信噪比),相同干扰功率(干信比0 dB)的不同干扰方式作用下的伪码调相引信输出仿真结果如图9所示。其中,瞄准式干扰采用载波频率对准引信发射信号中心频率的正弦波调幅信号,扫频式干扰采用扫描带宽覆盖引信工作频带的正弦波调幅扫频信号。根据仿真结果,传统瞄准式及扫频式干扰同引信发射信号相干性较差,因此在经过引信相干解调后输出幅值约为0.2的类噪声信号。而基于DRFM的转发式及重构式干扰能够使引信输出相关峰。转发式干扰作用下引信输出相关峰幅值约为0.7,而重构式干扰作用下引信输出相关峰幅值约为1.2。这是因为干扰机截获信号包含环境噪声,因此转发式干扰受环境噪声影响导致干扰信号同引信信号相关性下降,而重构式干扰则能够抑制截获噪声对干扰效果的影响,保证干扰信号同引信发射信号的相干性。
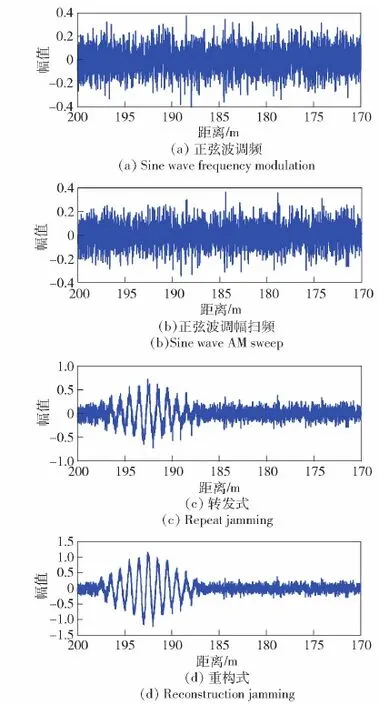
图9 不同干扰作用下伪码调相引信输出仿真结果Fig.9 The outputs of the BPCM fuze with different jamming effects
不同干扰方式成功干扰引信所需最小干信比仿真结果如表2所示。瞄准式干扰及扫频式干扰本质上是通过饱和引信接收机信道的方式使引信“早炸”或者“瞎火”,其对引信信号参数估计的要求较低,仅需要测得引信信号工作频段及带宽即可形成干扰,因此干扰效果受截获信噪比影响较小,不同截获信噪比条件下成功干扰引信所需功率差异较小。其干扰信号同引信发射信号相干性较差,因此需要较大的功率才能干扰成功干扰引信,瞄准式干扰成功干扰引信所需功率均值约为11.5 dBm,扫频式干扰成功干扰引信所需功率均值约为14.3 dBm。转发式干扰及重构式干扰则在截获引信发射信号的基础上,通过直接转发截获信号或者根据参数估计结果重构引信发射信号形成干扰,其干扰信号同引信发射信号高度相干,在高信噪比条件下所需干扰功率明现低于瞄准式及扫频式干扰,并且二者差异较小。在10 dB信噪比条件下转发式干扰所需干扰功率为-1.6 dBm,而重构式干扰所需干扰功率-1.7 dBm;在0 dB信噪比条件下转发式干扰所需功率为1.5 dBm,重构式干扰所需功率为-1.6 dBm。但当截获信噪比严重恶化时,转发式干扰由于受到截获噪声的影响,干扰信号同引信发射信号相干性急剧下降,因此所需干扰功率显著增加,在-10 dB信噪比条件下所需干扰功率8.9 dBm。而重构式干扰的干扰信号同引信发射信号仍然保持着较强的相干性,在-10 dB信噪比条件下所需干扰功率仅为0.3 dBm。

表2 干扰功率仿真结果Table 2 Simulation of the jamming power dBm
4.2 试验验证
在微波暗室环境下通过电子对抗静态试验验证了本文所提干扰方法的性能。试验时干扰机距离伪码调相引信6 m,干扰天线波束主板同引信天线对准,干扰功率为0 dBm,环境噪声功率分别为-10 dBm和0 dBm。干扰系统采用美国是德科技公司生产的M9203A数字接收机及N5193信号源模拟,参数估计通过上位机实现,环境噪声采用美国是德科技公司生产的E8257D射频信号源模拟,引信载波频率3 GHz,调相带宽50 MHz。干扰系统截获信号及干扰作用下引信的输出如图10所示,图10(b)、图10(c)中绿线为重构式干扰作用下响应,黄线为转发式干扰作用下响应。从试验结果中可以看出,当环境噪声为-10 dBm时,相同功率转发式干扰及重构式干扰作用下均能够使引信输出相关峰,且二者输出功率接近,相关峰幅值均约为 100 mV。而当环境噪声增大到0 dBm时,转发式干扰作用下引信输出相关峰幅值约为50 mV,而重构式干扰仍保持约为100 mV。
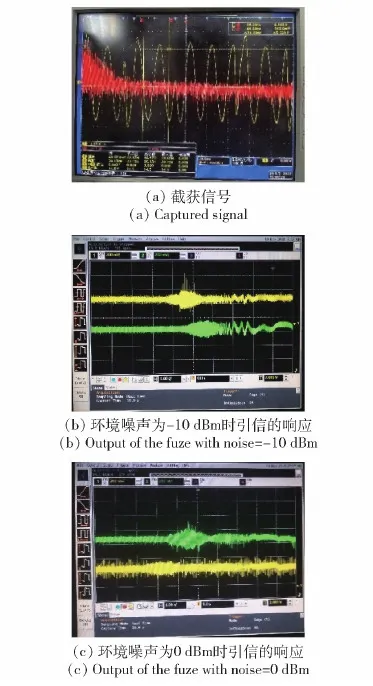
图10 干扰作用下引信的响应Fig.10 Outputs with jamming
5 结论
本文针对重构式干扰面临的低截获信噪比条件下伪码调相信号盲参数估计问题,提出基于变分正则化的伪码调相信号参数估计方法。该方法将伪码调相信号参数估计分解为载频估计及伪码序列估计两个子问题。在利用插值傅里叶算法精确估计信号载波频率后,将截获信号下变频为零中频信号;利用本文提出的基于稀疏增强正则项变分正则化迭代算法从零中频信号提取信号的伪码序列;根据参数估计结果重构引信信号形成干扰。通过仿真及试验验证了算法的参数估计性能及重构式干扰的干扰效果。得出以下主要结论:
1)根据仿真结果,基于稀疏增强正则项的变分正则化算法通过检测零中频信号幅值跳跃从零中频信号提取伪码序列,在-5 dB截获信噪比条件下伪码序列估计准确性超过95%,在-10 dB截获信噪比条件下估计准确性仍高于75%。
2)基于本文所提伪码序列参数估计方法的重构式干扰在低信噪比条件下干扰效果显著优于转发式干扰及其他预置波形干扰,-10 dB截获信噪比条件下成功干扰伪码调相引信所需干扰功率比转发式干扰低8.8 dB。
3)在0 dBm截获噪声条件下,重构式干扰作用下引信输出相关峰能量明现高于转发式干扰。

