尾部形状对超空泡射弹尾拍运动影响的数值研究

刘如石, 郭则庆, 张辉

(南京理工大学 瞬态物理国家重点实验室, 江苏 南京 210094)

0 引言

超空泡射弹是利用超空泡原理、由火炮发射攻击水下目标的水下超高速弹药。超空泡射弹在水下高速运动时头部产生的超空泡完全包裹弹体,可使其水下运动阻力减小90%以上[1]。通过对射弹的流体动力外形进行合理设计可以实现超空泡射弹在水下无动力、无控制方式下稳定航行较远距离并毁伤目标[2]。超空泡射弹在水下高速运动时受到扰动(如发射时受到的扰动或者从空中入水时受到的扰动等),可能使射弹在运动过程中发生弹尾与空泡壁面的周期性碰撞,这种现象称为尾拍运动[3]。不同于空中飞行的射弹,超空泡射弹保持水下运动稳定的主要方式是尾拍运动。近年来,这种特殊的稳定运动方式受到了广泛的关注和研究。

早期关于超空泡射弹尾拍现象的研究主要基于试验和理论计算。Rand等[4]通过建立动力学理论模型研究了超空泡射弹尾部与空泡壁面周期性碰撞的尾拍规律,发现射弹在水中的尾拍运动类似于绕其头部空化器摆动,且尾拍频率与射弹速度呈反比,并且初始尾拍角速度越大,尾拍次数越多。 Logvinovich[5]通过水下射弹自由飞行试验拍摄到射弹尾拍形成的蛇形空泡,获得了水下高速射弹弹道变化规律。Ruzzene等[6-7]假设射弹以空化器中心为支点往复转动,建立了超空泡射弹的尾拍动力学理论模型,研究了射弹的尾拍运动规律,并将射弹设为细长弹性杆,研究其在尾拍冲击载荷作用下的结构响应特性。Putilin[8-9]结合理论分析和试验结果建立了超空泡射弹水下运动的数学模型,研究了空泡内部空腔对超空泡射弹水中尾拍运动特性影响。Mansour等[10]结合试验和数值模拟方法研究了不同空化器形状射弹的流场形态和阻力系数,发现半球形空化器的射弹阻力系数最低,并通过优化空化器形状提高了射弹航速。Saranjam[2]分别采用试验和数值仿真方法研究了初速为80 m/s的超空泡航行体在水下的运动规律。Wang等[11]基于一般动力学理论建立了超空泡航行体6自由度运动的模型,理论分析了超空泡射弹的尾拍运动失稳机理。 Jiang等[12]通过试验研究了不同头部和尾部形状对通气超空泡航行体阻力的影响。然而,由于超空泡射弹的速度极高给水下试验和测试增加了极大的难度,射弹尾拍过程中的水动力精确计算的理论方法也尚不完善,试验和理论方法研究的准确性不高。

近年来,随着计算流体力学(CFD)技术的发展,尤其是多相流数值模型的完善,数值模拟方法也在超空泡射弹尾拍运动研究中得到了广泛应用。姚忠等[13]采用CFD方法对射弹流场与弹道耦合计算,研究了初始扰动对超空泡射弹尾拍过程中流体动力特性和弹道特性的影响。梁景奇等[14]采用CFD动网格移动计算域技术,研究射弹不同初始速度下的尾拍运动特性。赵成功等[15]通过数值模拟方法,研究了质心位置对超空泡射弹尾拍运动的影响规律。陈伟善等[16]基于数值模拟方法,研究空化器形状对超空泡射弹尾拍运动的影响规律,并对比分析了不同空化器射弹的尾拍运动稳定性。祝许皓等[17]采用数值模拟方法研究了初始偏航角和滚转角速度对射弹尾拍运动的影响。侯东伯等[18]通过水洞试验研究了弹性尾缘航行体模型在不同压差系数、不同通气率下的空泡形态与压力脉动。马文轩等[19]采用数值模拟方法研究了射弹头部几何形状与空泡形态和阻力系数之间的关系,并通过优化弹头形状使射弹阻力系数减小30%。

目前对射弹尾拍运动特性的研究主要集中于初始运动状态和射弹总体外形、质量分布对其的影响,而射弹在尾拍运动过程中,尾拍力主要来自于弹尾与空泡壁面发生反复的碰撞,弹尾对射弹尾拍力的形成和尾拍运动特性具有直接和重要的影响,但相关研究却鲜见报道。本文应用有限元分析软件,基于CFD方法,采用动网格移动计算域技术研究了圆柱、尾锥、尾裙以及尾翼4种尾部结构形状的射弹在尾拍运动过程中的动力和运动特性,讨论了射弹尾部形状对尾拍运动的影响,对比分析了4种射弹的减阻效果,研究结果可为超空泡射弹的外形结构设计提供参考。

1 数值模拟方法

1.1 控制方程

超空化流场的数值模型涉及气液两相流动、湍流流动以及气液两相间的质量输运。本文基于有限体积法和Mixture多相流模型结合动网格技术构建了三维自由尾拍运动仿真模型。

混合相的连续性方程:

(1)

(2)

(3)

式中:t为时间;ρm为流体混合密度;vm为混合速度;n为相数,本文只考虑液态水和水蒸气两相,n=2;αi、ρi和vi分别为第i相的体积分数、密度和速度。

动量守恒方程:

(4)

(5)

式中:p为压力;g为重力加速度;F为体积力;μm为混合黏性系数;vdr,i为第i相的漂移速度,在均质平衡流中vdr,i=0,因此式(4)中等号右侧最后一项为0。

能量方程:

(6)

式中:Ei为单位质量第i相的总能,对于可压缩相,

(7)

hi为第i相的焓;keff为有效导热率;T为温度;hj,i为第i相中物质j的焓;Jj,i为第i相中物质j的扩散通量;τeff为有效黏性耗散率;Sh为体积热源。

射弹在水中的高速航行过程属于高雷诺数流动,湍流会对空化流场和流体动力产生一定影响,选择具有较高精度和数值稳定性的Realizablek-ε湍流模型进行计算。

湍流强度k方程:

(8)

湍流耗散率方程:

(9)

式中:ρ为流体密度;v为速度矢量;μ为流体的时均速度;μt为湍流黏性系数,μt=ρCμk/ε,Cμ=0.09;σk=1.0;Gk、Gb分别为速度梯度和浮力引起的湍动能;Sk、Sε为源相;C1=max [0.43,η/(η+5)],η=Ek/ε,E为时均应变率;C2=1.9;σε=1.2;ν为运动黏度。

射弹在水下运动时水发生自然空化,涉及汽、液两相的变化,采用Schnerr-Sauer空化模型来模拟,其具体输运方程为

(10)

(11)

1.2 数值方法验证

图1 仿真空泡与试验空泡对比Fig.1 Comparison of simulated cavity and experimental cavity

图2 仿真数据与试验数据对比Fig.2 Comparison of simulated data and experimental data

1.3 模型及网格划分

图3 射弹模型Fig.3 Projectile models

本文主要研究圆柱、尾锥、尾翼和尾裙4种尾部形状对射弹运动特性的影响。所采用的4种射弹模型除尾部形状差异外,其他参数均相同,如图3所示。表1给出了射弹主要几何与质量参数。

为避免边界效应对射弹附近流场产生影响,计算域选取φ20L×30L(L为弹长)的圆柱形流域,边界条件设置如图4所示,入口边界速度设置为 0 m/s,出口边界压力设置为140 325 Pa(4 m水深压力)。射弹初始位于水深4 m处,以1 000 m/s的初始水平速度和一定的初始尾拍角速度自由运动。采用移动计算域的动网格模型,以射弹建立体坐标系,计算域跟随射弹一起运动,通过6自由度求解器解算射弹的平动速度和绕质心转动角速度;而流场固连于地面坐标系,初始设定为静止状态。采用此方法可大幅降低网格数量,并可以避免常规动网格的网格更新与重构引起的误差,有效提高计算精度和计算效率。由于本文中给定的初始运动状态相对于Oxy平面对称,且由于流场的对称性,射弹在运动过程中绕x轴和y轴转动量很小,可以忽略不计,为简化分析,射弹限制在Oxy平面内平动,且只能绕z轴转动。图4中v0和ω0分别为射弹的初始速度和初始角速度。

表1 射弹主要参数Table 1 Main projectile parameters

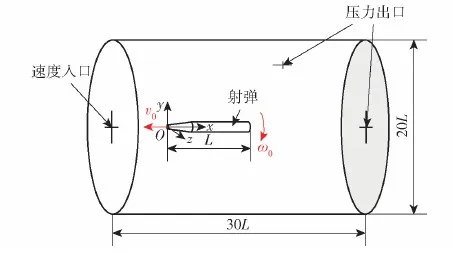
图4 计算域及边界条件示意图Fig.4 Computational domain and boundary conditions

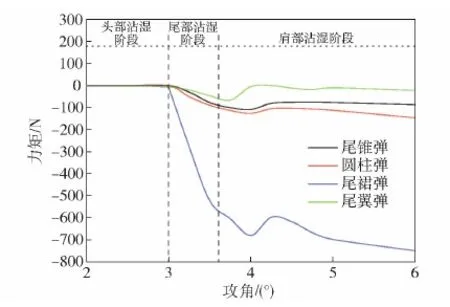
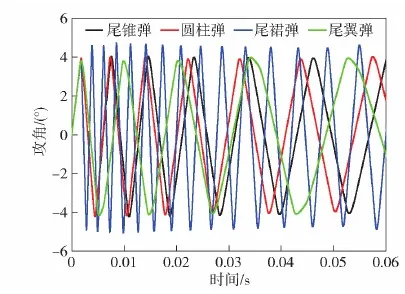
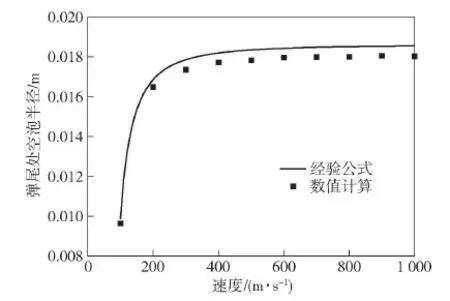
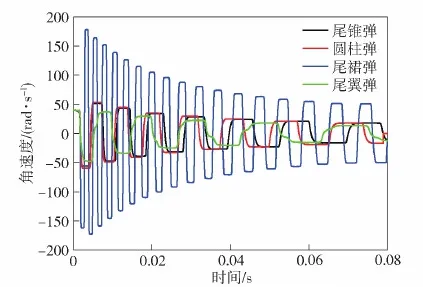
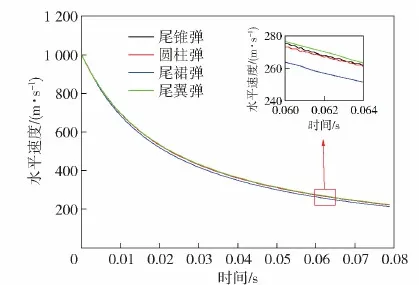
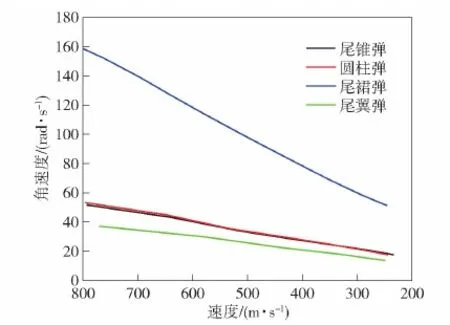
计算网格采用结构化网格划分方式,如图5所示。对弹体附近进行加密,边界层网格厚度为 6.5×10-6m,保证30

图5 网格划分Fig.5 Meshing of computational domain

图6 网格无关性验证Fig.6 Grid independence verification

2 计算结果与分析

2.1 尾拍运动过程中的空泡变化

射弹在尾拍运动过程中,随着攻角增加,弹体的沾湿状态可分为3个阶段:1)弹头沾湿阶段,除弹头空化器以外弹身全部包裹在空泡内;2)弹尾沾湿阶段,射弹尾部刺入空泡壁,沾湿面积随攻角增大而增大;3)肩部沾湿阶段,射弹肩部沾湿,同时在沾湿部分形成二次空泡并包裹后部弹体,降低弹尾沾湿面积。

图7给出了3个阶段下的空泡形态及表面压力云图对比。其中图7(a)所示为射弹处于弹头沾湿阶段的空泡形态,此时射弹空化器触水产生超空泡完全包裹后部弹体,由于4种射弹空化器形状相同,因此其产生的空泡形状也一致。

图7 3种尾拍阶段下的空泡形态及表面压力云图对比Fig.7 Comparison of cavitation shape and surface pressure in three tail-slap stages

图7(b)给出了射弹处于弹尾沾湿阶段的空泡形态,Ft为射弹尾部受力,此时射弹尾部浸入水中,产生二次空泡,在相同攻角下,由于射弹尾部形状的差异,导致其尾部沾湿面积不同,沾湿产生的二次空泡形态各异。其中尾裙弹尾部沾湿面与射弹速度方向夹角较大,产生的二次空泡也较明显,而尾翼弹由于仅单个翼片浸入水中,沾湿面积最小,产生的二次空泡最小。

随着城市化进程的不断深入，建筑工程的数量与规模在不断增加。由于受到建筑面积的制约，部分建筑物被建造在地质较差的地面上，导致工程事故频发。地基施工属于土建工程的基础环节，基础与地基均属于隐蔽工程，一旦没有得到及时有效的检查，极可能引发工程事故，产生无法弥补的后果。因此，对地基基础施工与加固技术的研究很有必要，不但能够促进施工技术的更新优化，而且对整个建筑行业的健康发展来说也具有十分重要的意义。

图7(c)所示为射弹处于肩部沾湿阶段的空泡形态,此时射弹肩部沾湿产生二次空泡包裹了后面部分弹体,降低了弹尾沾湿面积。不同于尾锥弹和圆柱弹,尾裙弹和尾翼弹弹尾的先收缩后扩张结构在弹尾产生了4次空泡,弹尾收缩段包裹在空泡内部,因此其沾湿面积明显小于其他两种弹型。

2.2 尾拍流体动力特性比较

图8给出了射弹尾拍运动过程中3种沾湿状态的受力,其中Fh和Fs分别为空化器受力和射弹肩部受力,G为重力。射弹在弹头沾湿阶段,仅受到弹头阻力和重力作用,此时射弹受到的俯仰力矩很小,可以忽略;射弹到达弹尾沾湿阶段时,弹尾沾湿受力,产生抑制攻角增加的回转力矩;随着射弹尾拍攻角进一步增加,射弹肩部沾湿受力,此时射弹处于肩部沾湿阶段,由于肩部沾湿面处于质心前方,因此其沾湿受力产生了促进攻角增加的倾覆力矩,与弹尾沾湿产生的回复力矩互相影响。

图8 3种尾拍运动状态下的受力分析Fig.8 Force analysis under the three stages of tail-slap

由于射弹尾部形状的区别,射弹在尾拍过程中的尾部沾湿面积不同,产生的尾拍力和力矩也有一定差异。图9为通过计算得到的4种射弹在速度1 000 m/s时不同攻角状态下所受的力矩,可以看出,射弹尾部几何形状对其在尾拍运动过程中的流体动力影响显著,在相同攻角下,射弹所受力矩对比为尾裙弹>圆柱弹>尾锥弹>尾翼弹。结合图7进行分析各沾湿阶段的受力特点,可以得出以下3点:

1)在弹头沾湿阶段,射弹尾部均被空泡完全包裹,且射弹弹头几何形状相同,因此此时4种射弹受力状态相同,且所受力矩几乎为0 N·m。

2)在弹尾沾湿阶段,4种射弹均受到了抑制攻角增大的回转力矩,其中尾裙弹受到的力矩明显大于其他3种弹型,其主要原因是尾裙弹的尾部沾湿面与射弹速度方向夹角较大,产生了较大的表面压力,如图7(b)所示,且沾湿面受到的压力合力方向与射弹轴线方向夹角接近垂直,使其所受力矩较大;而尾翼弹虽然尾翼前翼面所受压力较大,但受力面积很小,且受力方向与弹轴方向夹角较小,因此其所受力矩最小;尾锥弹的尾部锥段在尾拍时未沾湿,降低了尾部沾湿面积,从而使其所受力矩小于圆柱弹。

3)在肩部沾湿阶段,肩部沾湿会产生促使攻角增加的倾覆力矩,由于4种射弹肩部几何形状一致,因此其在相同攻角下肩部沾湿产生的力矩相同。从图9的力矩曲线可以看出,每种射弹均在特定攻角范围内力矩曲线回升。其主要原因是由于4种射弹尾部结构的差异,随着攻角的变化,尾部沾湿产生的力矩大小与变化趋势均不同,并且肩部沾湿产生的二次空泡对尾部沾湿影响也各异,使射弹在肩部沾湿产生与尾部沾湿产生的力矩方向相反的倾覆力矩时,4种射弹所受合力矩回升的攻角范围与回升幅度各不相同。

图9 力矩随攻角变化Fig.9 Torque variation with angle of attack

定义射弹的阻力系数、升力系数和力矩系数分别为

(12)

(13)

(14)

式中:Fd、Fl分别为射弹的的阻力和升力;ρ0为水的密度,取998.2 kg/m3;v为射弹当前运动速度;S为射弹空化器面积;M为射弹的力矩。

为了对比弹尾形状对射弹尾拍运动过程中流体动力的影响,计算4种射弹在初速1 000 m/s、初始尾拍角速度40 rad/s条件下的飞行过程。图10为飞行过程中力矩系数随时间变化曲线。由图10可以看出:4种射弹力矩系数曲线均呈现出周期性振荡变化,说明它们在航行过程中均有相对稳定的尾拍往复运动状态;力矩系数在射弹经历一至两次尾拍后,振荡幅值趋于稳定,并且4种射弹力矩系数峰值从大到小依次为尾裙弹、圆柱弹、尾锥弹、尾翼弹,且尾裙弹力矩系数峰值远大于另外 3种弹型。

图10 力矩系数对比Fig.10 Comparison of torque coefficients

图11、图12分别给出了4种射弹的升阻力系数及其峰值随时间变化对比。由图11和图12可以看出射弹的升阻力系数均呈现脉冲式周期性状态:当射弹被空泡完全包裹时升阻力基本都由头部空化器产生,并达到最小值,因此4种射弹的升阻力系数最小值基本一致;当弹体尾部刺穿空泡壁面并浸入水中时,流体阻力和升力显著增加,在射弹攻角达到最大值时也达到峰值;前两次尾拍升阻力系数峰值迅速增加,最终保持在相对稳定的区间内。尾裙弹的升阻力系数峰值均远大于其他3种弹型,其主要原因有两点:1)由于尾裙弹尾部的扩张结构,使其在相同攻角下,沾湿面与水流相对速度方向夹角最大,从而产生了更大的冲击压力,计算结果表明,尾裙弹的尾部表面最大压力最大可达50 MPa,是圆柱弹的 5.6倍;2)尾裙弹尾拍时产生的力矩较大,使得射弹尾拍产生的最大角动量也最大,其尾拍时最大攻角增加,进一步增加了尾部沾湿面积,从而产生了较大的升阻力。

图11 阻力系数对比Fig.11 Comparison of drag coefficients

图12 升力系数对比Fig.12 Comparison of lift coefficient

2.3 弹道特性对比

图13给出了4种射弹尾拍运动过程中攻角随时间的变化,可以看出,4种射弹都是通过尾部往复撞击上、下空泡壁的双侧尾拍模式达到运动稳定,攻角曲线均呈现出周期性振荡变化规律,且振荡幅值几乎不变。由于射弹尾拍时,尾部沾湿面浸入水中深度较小,因此其尾拍最大攻角与射弹尾部空泡直径相关。图14所示为根据文献[21]所得的经验公式计算与数值模拟得到的弹尾处空泡半径随射弹速度的变化对比,可以看出数值模拟得到的空泡半径略小于经验公式,但变化趋势一致。分析空泡半径随速度的变化趋势可以看出,虽然空泡最大直径和长度都随着速度发生变化,但当射弹速度大于 250 m/s 时,射弹尾部位置的空泡直径几乎不变。因此,射弹0.06 s之前(速度均大于250 m/s)的尾拍最大攻角几乎保持不变。然而,尾裙弹尾拍时攻角峰值略大于其他3种弹型,其原因是其在尾拍过程中尾拍频率和角速度远大于另外3种弹型,尾拍角动量较大,射弹尾部浸入水中较深,导致其尾拍攻角峰值较高。

图13 攻角变化对比Fig.13 Comparison of angle of attack

图14 经验公式与数值计算得到射弹尾部空泡半径 随速度的变化对比Fig.14 Variation of the radius of cavitation at the tail of projectile with velocity calculated by empirical formula and numerical simulation

图15 角速度变化对比Fig.15 Comparison of angular velocities

图16 尾拍频率变化对比Fig.16 Comparison of tail-slap frequencies

图15、图16分别为4种射弹在尾拍运动过程中角速度和尾拍频率随时间的变化规律,结合两幅图对比可以看出,4种射弹的角速度变化曲线均呈现出相似的振荡特性。射弹尾拍时受到的力矩越大,其尾拍角速度峰值越大,尾拍频率越高。在射弹尾拍运动初期,尾裙弹尾拍频率和角速度峰值迅速增加,到达极值后随时间逐渐减小,另外3种弹型呈现出尾拍频率随时间递减的规律。产生这种现象的主要原因是40 rad/s的初始角速度远小于尾裙弹在此航行速度下其固有尾拍运动状态的角速度峰值,因此尾裙弹在初期尾拍过程中角速度迅速增加至固有尾拍角速度峰值,导致其尾拍频率在尾拍初期迅速升高,而另外3种弹型在初始状态下的固有尾拍角速度峰值接近40 rad/s,因此其在尾拍初期角速度峰值与尾拍频率未发生剧烈变化。

图17所示为4种射弹的速度衰减曲线。从图17 中可以看出,4种尾部结构的射弹速度衰减速率从大到小依次为尾裙弹、圆柱弹、尾锥弹、尾翼弹,其中尾裙弹与尾翼弹在航行至30 m处速度相差8.8%,由此可知,射弹的尾部结构对射弹的减阻效果影响较大,对尾部结构的优化设计可以进一步提高射弹的射程。

图17 速度衰减曲线Fig.17 Velocity attenuation curves

2.4 超空泡射弹水下稳定运动特性

图18 不同初始角速度下角速度随速度的变化Fig.18 Variation of angular velocity with velocity under different initial angular velocities

为研究射弹尾拍运动过程初始角速度对尾拍运动的影响规律,研究4种射弹在初速为1 000 m/s、初始扰动角速度分别为40 rad/s、100 rad/s、200 rad/s 3种工况下的尾拍运动状态。图18所示为4种射弹角速度随速度变化曲线,可以看出4种射弹在 3种初始角速度下都可以稳定航行。每种射弹即使初始尾拍角速度差异较大,在经历两次尾拍之后,其角速度趋于一致,即每种射弹的运动角速度沿特定的包络线振荡,且该包络线与初始运动状态无关,射弹的这种尾拍运动状态可以称为其固有尾拍运动状态。图19给出了4种射弹在尾拍稳定后,角速度振荡曲线的上包络线对比,可以看出4种射弹包络线均近似为直线,且尾拍角速度峰值越高,其随速度衰减越快。

图19 尾拍稳定后角速度振荡上包络线Fig.19 Upper envelope of angular velocity oscillation after the tail is stabilized

结合图18、图19可以看出,尽管本文研究的射弹的尾部结构截然不同,但4种射弹尾拍运动均存在固有尾拍运动状态,在射弹能够稳定航行的前提下,射弹的固有尾拍运动状态与射弹的尾部几何形状有关,而与射弹的初始扰动角速度和初速无关,并且射弹处在固有尾拍运动状态时,射弹尾拍角速度振荡峰值随速度的衰减正比例减小。射弹的这种尾拍运动特性对水下超空泡射弹几何设计以及水下弹道解算有一定指导作用。

3 结论

本文基于有限体积法和Mixture多相流模型并结合动网格技术,比较了圆柱、尾锥、尾翼和尾裙 4种尾部结构射弹的尾拍运动特性,分析了产生运动差异的主要因素。得出主要结论如下:

1)射弹在尾拍时其尾部几何形状的差异,会导致沾湿面产生的空泡形态不同。沾湿面与射弹航行速度方向夹角越大,产生的空泡尺寸越大。尾裙弹和尾翼弹尾部的先收缩、后扩张结构在肩部沾湿阶段产生了4次空泡,可有效降低尾部沾湿面积。

2)尾部几何形状对超空泡射弹尾拍受力影响较大,相同攻角和航速下4种射弹所受力矩大小为尾裙弹>圆柱弹>尾锥弹>尾翼弹,影响射弹尾拍时受力的主要因素为:射弹尾拍时的尾部沾湿面积、沾湿面与射弹航行速度方向之间的夹角以及沾湿面产生力的方向与弹轴之间的夹角。

3)4种射弹在尾拍运动过程中,相同攻角下尾部沾湿产生的力矩越大,射弹尾拍运动越剧烈,航行速度衰减越快。

4)4种弹型射弹都存在与射弹的尾部几何形状有关,而与其初始扰动角速度无关的固有尾拍运动状态,并且射弹处在固有尾拍运动状态时,射弹尾拍角速度振荡峰值随速度的衰减正比例减小。