计及转供电概率的主动式配电网网格化规划方法

俞晓峰，肖旋科，张中超，谢旭泉

（广东电网有限责任公司 河源供电局，广东 河源 517099）

0 引言

配电网是贯穿社会经济与能源系统的关键系统，其存在与发展不仅可满足人们的用电需求，而且能维持国家的稳定运转。然而，随着太阳能、风能等分布式电源的接入，整个电网能源供应的可靠性与运行的稳定性受到了严重的冲击。为保障我国配电网可靠、灵活地运行，同时实现电网能源保质、保量的配送，配电网的网格规划研究变得越来越重要。针对网格规划的研究中，李小明等［1］以线路中的最小损耗费为目标，设计一种中低压配电网网格化规划模型，并通过粒子群算法求解模型，解决传统配电网规划方法规划效果不理想的问题；刘峰等［2］针对传统主配网规划方法受小截面线路的影响，无法完成负荷聚类分块的问题，设计一种基于三维视频编码的配电网网格化规划方法，实现了负荷性能的突破；侯佳等［3］基于容量与供电可靠性的双Q 理论设计的配电网网格化规划方法，实现了供电可靠性与经济性之间的平衡。在我国城市电网的发展进入主动式配电网阶段的重要时期，如何构建高效、合理的主动式配电网网格化规划方案，在一定程度上决定了一个城市未来的发展，因此本文针对该课题进行的研究具有重要的现实意义。

1 主动式配电网网格化设计方案

1.1 计算主配网线路转供电概率

当下，我国城市主动式配电网的运行方式变化极快，但由于缺少高精度的量测装置，因此进行主动式配电网网格化规划时，难以获取整个配电网的实时拓扑，而配网拓扑先验信息是网格化规划的基础，所以本文根据智能电表采集到的节点电压、电流等数据，计算主动式配电网线路的转供电概率，为网格化规划奠定理论基础。计算主配网线路转供电概率时，需要对采集的原始信息数据进行清洗，受配电网运行环境与量测装置误差等因素的影响，原始采集数据存在丢包、误码等现象，与真实数据存在严重偏差，影响转供电概率的计算精度。为降低数据噪点，通过一阶差分计算时序负荷增量，其表达式为

其中：ΔPi表示主动式配电网节点i的负荷增量；Pi(t)表示主动式配电网节点i在t时刻的负荷幅值；Δt表示时间变化量。在公式（1）的基础上，对负荷数据进行归一化处理，再将其映射至对应的N个不同的整数值，即可去除原始数据中的噪点与绝对误差，其表达式为

其中：P′i表示去除噪声点与误差后的主动式配电网节点i的负荷幅值；ΔPimin、ΔPimax分别表示主动式配电网节点i在t时刻的负荷幅值中的最小值与最大值。

在我国主动式配电网运行过程中，由于联络线的转供容量有限，导致配网的转供电成为一个概率事件。同时，主配网各线路获得供电恢复的优先级也各不相同，所以为实现主动式配电网的网格化规划，需要计算主配网的线路转供电概率［4］。由于主动式配电网的负荷数据属于随机变量，所以通过公式（3）所示的正态分布计算方法近似反映主配网线路的主供电概率［5］：

其中：f(P′i)表示主动式配电网负荷的正态分布，即主配网线路的转供电概率；ε2表示方差；δ表示数学期望。

综上，在采集主动式配电网负荷数据的基础上，计算出主配网线路转供电概率，为后续网格化规划提供数据支撑。

1.2 计及转供电概率确定线路优先级

进行主动式配电网网格化规划的关键在于确定线路优先级，只有确定了配电网内部所有线路的优先级，才能逐条分析线路是否可转供，再根据转供线路进行配电网的网格化规划［6］。本文在确定主动式配电网的线路优先级时，综合考量馈线安全电流和重载率、线路上的联络点到馈线的距离和馈线所能输出的最大线径，然后进行优先排序［7］。通常，假设一条即将停电的10 kV 馈线上有多个联络点可供选择时，电力系统会根据之前所解析的主网和配网的线路连接关系和线路基础信息计算出多条线路叠加后的电流（即转出馈线的电流量），再将转出馈线的电流量与线路上的安全电流进行对比，即可判断发生重载现象的线路，进而求出重载率，其计算公式为

其中：μ表示主动式配电网的重载率；N0表示最大负载超过60%的配电网线路数量；N1表示主动式配电网中线路的总数量。

根据公式（4）求出重载率即可确定各线路可转供的合理值，最后还需要获取主动式配电网的转供路径。我国主动式配电网因为运行方式的改变，导致拓扑结构具有一定的随机性，所以对线路优先级进行排序需要搜索转供路径。本文主要采用广度优先搜索算法，具体流程如下：首先，在主动式配电网中随机选择一个节点作为根节点，以该节点作为转供路径搜索的初始点；其次，依次搜索和根节点邻接且未被访问过的子节点，从而生成转供电路径；最后，对各节点相应的编号进行记录，当全部节点均被访问过，本次搜索结束，得到配电网线路的转供电路径。综合考虑配电网线路的转供路径与各线路重载率，即可对线路的优先级进行排序［8］。按照搜索的路径进行转供电时，一般重载率越小的线路被转供电的概率越大，排在的位置越靠前，以此完成线路优先级的排序。

1.3 主动式配电网网格化规划

确定主动式配电网各线路的优先级后，由规划人员按照分支线规划原则进行配电网的分支线规划，再综合考虑主配网内的负荷，进行配电网的网架规划［9］。为实现主动式配电网的网架规划，本文以全寿命周期成本为目标函数，其表达式为

其中：F表示主动式配电网网架规划的目标函数；B0表示主配网主干线m的初始投资成本；B1表示主配网主干线m的年维修成本；B2表示主配网主干线m的年网损成本；B3表示主配网主干线m的年停电损失成本；λ表示贴现率；γ表示主配网主干线m的使用寿命。

在公式（5）所示的全生命周期成本模型的基础上，利用Dijkstra 算法求解，该算法是一种常规寻优算法，通过该算法对主动式配电网网架规划模型的解空间进行遍历搜索，即可得到主动式配电网网架的最佳规划方案。通常，传统主动式配电网网格化规划主要分网格划分与网架规划2个部分，这种单一规划的结果容易陷入局部最优，缺少整体性，所以本文在进行主动式配电网的网格化规划时，引入供电单元与网架结构的匹配模型，整合网格划分与网架规划，实现网格划分与网架规划一体化［10］。供电单元是综合考虑主配网负荷密度、负荷特性等相对独立的单元，为了在满足供电单元内部负荷需求的基础上，实现网架结构规划最优，需要进行供电单元和网架结构的匹配。构建负荷均衡的目标函数的表达式为

其中：H表示主动式配电网网架的负荷均衡指数；Qj表示主配网中第j条支线的视在功率；Qjmax表示主配网中第j条支线允许通过的功率最大值；m表示主配网中支线的数量。利用公式（6）所求配电网网架的负荷均衡目标函数，即可实现供电单元和网架结构的匹配。

综上所述，本文设计的适用于主动式配电网发展特点的一体化规划流程［11］如下：首先，结合主动式配电网的运行特点，将主配网划分为供电网格与供电单元；其次，进行主配网的网架规划；最后，基于公式（6）对供电单元与网架规划进行匹配，得到最佳匹配方案后，即可实现基于网格划分与网架规划一体化的主动式配电网网格化规划方案。

2 实例分析

2.1 规划区概况

本文选取某市开发区主配网的网格化规划作为测试算例，验证设计的计及转供电概率的主动式配电网网格化规划方法的有效性与正确性。实例规划区域总占地面积约138.3 km2，按用地性质进行划分，可以将本次规划区划分为6种用地类型：工业用地为10.9 km2，占规划区总用地的7.88%；商业用地为23.4 km2，占规划区总用地的16.92%；公共管理与公共服务设施用地为17.5 km2，占规划区总用地的12.65%；住宅设施用地为41.2 km2，占规划区总用地的29.79%；仓储设施用地为6.7 km2，占规划区总用地的4.84%；其他类型设施用地为38.6 km2，占规划区总用地的27.91%。将上述规划区域的地理信息及相关用地信息作为本次实例研究的基础信息，为后续城市主配网的网格化规划提供了参考数据。与此同时，调查规划区的配电网基本概况，得到表1的规划区变电站情况。

表1 规划区变电站情况

如表1所示，规划区配电网共设置了220 kV变电站3座、110 kV变电站5座，不仅各变电站重载情况严重，而且变电站间隔利用情况不均衡。因此，需要采用本文的设计方法对规划区的主配网进行重新规划。

2.2 规划结果分析

根据本文设计方法所得的实例规划区主动式配电网网格化规划结果如图2所示。在本文设计方法的规划下，规划区的配电网共计新增3 座110 kV 变电站，退运1 座220 kV 变电站。整个规划区的供电网格共分为3 个区域：城北网格、城中网格、城南网格，具体规划成效见表2。

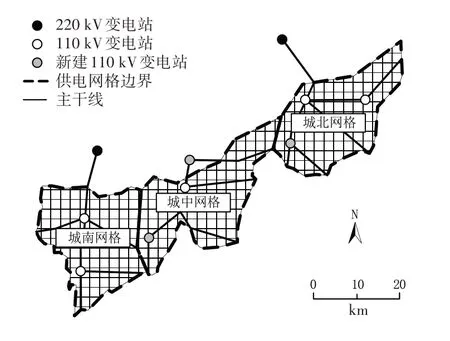
图2 规划区主动式配电网网格化规划结果

表2 规划区主动式配电网网格化规划成效表

通过相关计算，实例区域主动式配电网规划3个供电单元，规划前后的供电单元数量一致，但相应的网架结构有所不同。与规划前相比，规划后实例区域的主干线路减少了5 条，主干线路总长度减少了17.04%，同时线路联络率由规划前的84.21%提升至100%，说明本文设计的方法可以有效提升主动式配电网的线路利用率。此外，各供电网格之间相互独立，每一个供电区域的划分大小合理，供电可靠率由97.986 3%提升至99.657 4%，进一步验证了本文设计方法的科学性与合理性。

3 结语

针对我国主动式配电网日益复杂的问题，本文研究了计及转供电概率主动式配电网网格化规划方法，结合主配网的运行特点，计算线路的转供电概率，根据转供电概率确定线路优先级，再针对不同线路的优先级进行主配网的网架规划，实现配电网的网格化规划。实例研究结果表明，本文设计的方法具有较高的可行性与可靠性，可以为我国主动式配电网的优化提供借鉴。本研究目前仅进行了主配网的网格划分工作，还没有构建反映网格空间特征的数学模型，无法统筹分析区块负荷的增长趋势。未来的研究将针对此不足，继续完善主动式配电网网格化规划方法，提高配网建设与管理的水平。