基于VMD-MFE-PNN的电机轴承故障诊断方法

吕宗宝,牛豪康,谢子殿

(1.哈尔滨天源石化工程设计有限公司,哈尔滨150022;2.黑龙江科技大学 电气与控制工程学院,哈尔滨 150022)

0 引 言

滚动轴承作为机器设备中的一个常用部件,由于长期使用,易造成滚动轴承老化磨损,从而影响设备的整体运行。在所有电机机械故障中,很大比例的损伤是由轴承造成的。然而轴承振动信号具有较高的随机性和复杂性,在实际诊断中,很难准确地检测出各式复杂的轴承故障。

经验模态分解(empiricical mode decomposition, EMD)[1]及其改进算法以其正交性、收敛性等特点被广泛用于信号处理等领域。陈宗祥等[2]提出一种基于EMD和双谱分析的电机轴承故障诊断方法,其在对信号进行EMD分解前,先通过小波包分解进行信号的预处理,结合方差贡献率检验得到的分量,虽很好地解决了模态混叠等问题,但其前期处理工作较为繁琐。VMD是一种基于优化原理的信号分解方法[3],该方法将原始信号分解为k个稳定的模态函数,直接避免了EMD分解方法存在的模态混叠等问题。张建财等[4]通过VMD方法分解轴承故障信号,将所有分解得到的IMF分量的能量特征向量输入到概率神经网络中完成对轴承故障的识别。但该方法需要对VMD分解得到的所有IMF分量分别求其能量特征值,计算量大,且冗余信息较多。模糊熵(fuzzy entropy,FE)是用于衡量模糊集合中随机变量的不确定性的一种度量方法,其计算方式类似于信息熵,常被应用于处理滚动轴承的故障分类。汤占军等[5]在模糊熵基础上,将多尺度模糊熵作为故障特征输入到支持向量机算法中,完成了对风机轴承的故障诊断。

结合PNN训练过程自适应能力强、速度快的特点[6],提出一种基于VMD-MFE-PNN的电机轴承故障诊断方法,并与结合排列熵(permutation entropy, PE)和多尺度排列熵(multi-scale permutatin permutatim entropy, MPE)的VMD-PE-PNN、VMD-MPE-PNN、VMD-FE-PNN等诊断方法的准确率进行对比。

1 理论介绍

1.1 变分模态分解

VMD主要用于分离不同频率和振动模态的信号成分,其基本思想是将原始信号表示为一组局部频率和幅度调制的正弦函数的叠加形式,其中每个正弦函数称为一个模态。这些模态可以通过最小化具有约束条件的变分能量函数来求解[7]。

首先,构造VMD的变分问题。假设原始信号S被分解为k个分量,每个分量都是具有中心频率的有限带宽的模态函数,并且确保各模态函数的估计带宽之和最小。约束条件还要求所有模态函数之和等于原始信号。则相应约束变分表达式[8]为

(1)

式中:uk={u1,u2,…,uK}表示分解得到的IMF分量;ωk={ω1,ω2,…,ωK}表示各分量的中心频率。

然后,为求解约束变分表达式,引入惩罚参数α、Lagrange乘法算子λ,通过将具有约束条件的变分问题转换为非约束形式,得到增广Lagrange表达式[9]：

(2)

并在循环迭代过程中依据式(3)～ (5)更新uk、ωk、λ的值:

(3)

(4)

(5)

最后,给定精度ε,若满足式(6)的停止条件,则停止迭代循环,输出k个模态分量:

(6)

1.2 基于遗传算法对VMD参数进行优化

VMD算法需要人为设定预设参数(分解个数k和惩罚参数α),这些预设参数对分解结果非常关键[10]。为了克服这一限制,利用遗传算法来优化VMD的参数,以获得最佳的分解结果。

在寻优参数过程中适应度函数至关重要。熵值是一种用于衡量信号随机性和复杂性的指标,当噪声干扰较大或者信号复杂时,其熵值越大。峭度值反映了分量中的冲击性特征大小,其值越大表示分布更加尖锐和偏态,可能含有更多的故障信息。因此,为尽可能多地提取故障特征信息,本文选择构建一种综合函数,其相关表达式为

(7)

(8)

S=Ep(i)+1/abs(Ku(i)-3)

(9)

式中:N为采样点的个数;pi是包络a(i)的归一化形式;Ep(i)表示每个IMF的包络熵值;Ku(i)表示每个IMF的峭度值;S表示综合函数值;abs为绝对值函数。

结合包络熵值越小,峭度值越大,包含故障信息越多的特点,选择以最小的S值作为参数寻优的适应度函数:

minS=min[S(1),S(2),…,S(k)]

(10)

同时针对GA在初始种群或算法参数设置不合适时可能会陷入局部最优解的缺点,引入模拟退火算法对GA的选择操作进行改进,使其更容易跳出局部最优解,更快找出VMD最优参数组合。其参数优化过程如图1所示。

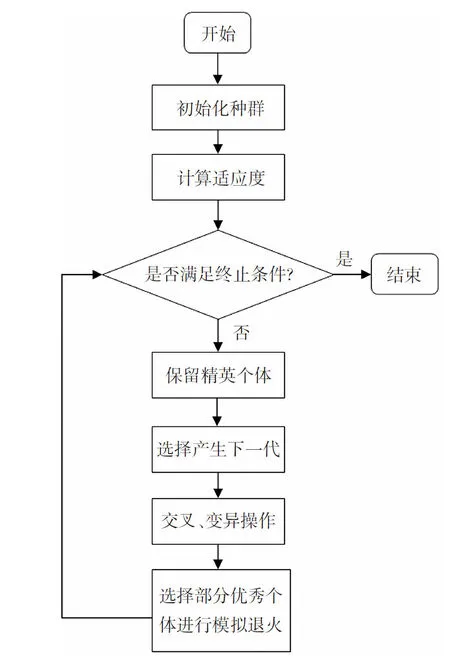
图1 SA-GA优化VMD流程图

1.3 峭度-相关准则

在GA完成对VMD的参数优化后,将优化后的参数(k,α)和其他参数输入到VMD中会得到一系列的IMF分量,直接对所有的IMF分量提取相关特征,信息计算量大,冗余信息较多,故选择其中包含故障信息最多的IMF分量单独进行分析。

轴承在发生故障时,其故障脉冲在时域内具有冲击特性,峭度指标能反映出其冲击性。结合相关系数可以确定信号之间相关性的特点,建立峭度-相关指标J来选择最佳IMF分量,J值越大,该分量所包含的故障信息越丰富,相应的表达式为

(11)

(12)

J=Ke·r

(13)

式中:Ke、r分别为峭度、相关系数;Ex为信号x解调后的包络信号;μe为Ex的均值。

1.4 多尺度模糊熵

多尺度模糊熵是一种用于分析时间序列复杂度和不规则性的方法。多尺度模糊熵是基于重叠子序列的概念计算的,但其引入了模糊逻辑的思想,可以更好地处理时间序列中的噪声和扰动。MFE比FE多了尺度因子τ,对于一个长度为M的时间序列{xi}={x1,x2,…,xM},给定维数n和梯度r,可以对其进行粗粒分割,形成新的粗粒向量:

(14)

最后,通过对粗粒分割后得到的向量进行逐一相对运算,就可以获得不同尺度下的分析结果。

1.5 概率神经网络

概率神经网络是一种基于贝叶斯决策理论的神经网络模型,旨在解决分类和回归问题。PNN主要由4层构成:输入层、模式层、总和层和输出层。

1.5.1 输入层

输入层接收由特征向量组成的输入信号。每个特征被视为一个节点,并将其值传递到下一层。输入层通常不进行任何处理,它只是传递数据。

1.5.2 模式层

模式层是PNN的核心部分,它通过在每个类别中估计样本的概率密度函数来实现分类任务。对于训练集中的每个类别,都会建立一个概率密度函数。具体而言,给定一个类别Ci,假设有m个训练样本x2,x2,…,xm,则该类别的概率密度函数表示为

(15)

式中:Kh是核函数。

1.5.3 总和层

总和层接收模式层的输出,并计算每个类别的总概率。具体而言,对于类别Ci,总和层会将模式层输出中所有属于Ci的概率相加,得到该类别的总概率。

1.5.4 输出层

输出层用于输出PNN对新样本的分类结果。通常情况下,输出层会输出具有最大总概率的类别作为分类结果。

2 故障诊断试验

2.1 诊断试验流程

提出基于VMD-MFE-PNN的滚动轴承故障诊断方法。首先将各状态下的轴承样本数据进行VMD分解,得到k个IMF分量;然后依据峭度-相关准则计算每个分量的J值,选择J值最大的作为最佳模态分量;最后计算该IMF分量的MFE值作为故障特征信息输入到PNN模型中,输出故障诊断结果。其诊断流程如图2所示。

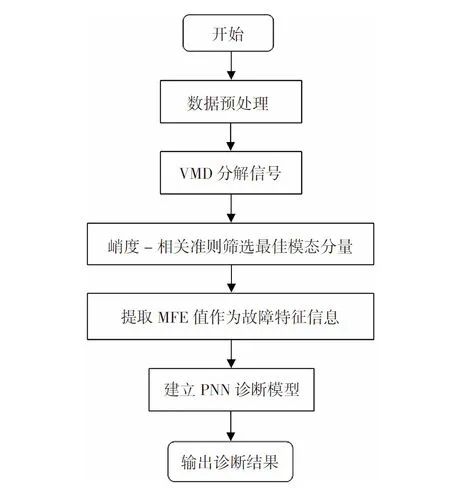
图2 诊断试验流程图

2.2 实际信号检验

使用的滚动轴承试验数据来自美国凯斯西储大学电气工程实验室,以此验证所提出方法的可行性和有效性[11]。试验所用的滚动轴承为6205-2RS JEM SKF型深沟球轴承,设置的3种故障(内圈故障、外圈故障、滚动体故障)的故障直径为0.533 4 mm,故障深度为0.279 4 mm,采样频率设置为12 000 Hz,电机转速为1 730 r/min。

以上述数据中的一段内圈故障信号为例,其原始时域信号如图3所示。采用改进遗传算法对VMD的参数进行寻优。遗传算法的参数设置为:种群规模30,迭代次数50。模拟退火参数设置为:初始温度100,温度降低参数0.98。寻优结果为:k=5,α=584,图4为VMD分解内圈故障信号的时域波形图。

图3 内圈故障时域图

图4 VMD分解信号时域图

根据峭度-相关准则计算各模态分量的J值,如表1所示。选择J值最大的IMF5作为最佳模态分量。

表1 VMD分解各模态分量J值

以相同的方法得到其他3种轴承状态的最佳模态分量,分别提取MPE值和MFE值。4种轴承状态的前20个时间尺度下的MPE值和MFE值分布情况如图5和图6所示。

图5 各种轴承状态下的MPE值分布情况

图6 各种轴承状态下的MFE值分布情况

由图5和图6对比可得,每种轴承状态所对应的最佳模态分量的MFE值相比MPE值按类别分层的现象更为明显。同时,针对4种轴承状态在时间尺度较大时呈现交叉无序且数值相差不大的现象,选取前6个尺度的MPE值和MFE值作为故障特征向量进行对比试验。

采样点数设置为4 096个,将每种轴承状态下的数据通过改变划分起点将其分为60份,共计240份样本数据,再将其按照2∶1的比例划分为160组训练集和80组测试集。在训练集和测试集构成的Excel表格中前6列表示每个样本前6个尺度下的MPE值或MFE值(PE值、FE值为单一时间尺度的熵值,仅对应Excel表格的第1列),第7列(第2列)表示每个样本所对应的轴承状态(1表示正常状态,2表示内圈故障,3表示滚动体故障,4表示外圈故障)。然后将其输入到PNN诊断模型中进行训练与测试,测试结果如图7、图8所示。

图7 VMD-MPE-PNN测试结果图

图8 VMD-MFE-PNN测试结果图

由图7、图8可知,以MPE值作为特征向量时,在滚动体故障和外圈故障均出现识别错误时,对应识别准确率为95%,整体故障识别率为97.5%。而以MFE值作为特征向量时,在滚动体故障测试样本中仅1组样本判断错误,轴承滚动体故障测试准确率为95%,其他轴承状态类型均判断无误,测试集整体识别故障准确率为98.75%。同时,结合单一尺度下的VMD-PE-PNN、VMD-FE-PNN诊断方法的准确率进行对比,不同诊断方法的准确率对比结果如表2所示。

表2 不同诊断方法的准确率对比

经上述分析可得,相较于在单一尺度下提取熵值作为故障特征向量,在多尺度下对滚动轴承故障信号进行特征提取的识别准确率明显提高。同时,以MFE作为故障特征向量的准确率最高。

3 结 语

提出一种基于VMD-MFE-PNN的电机轴承故障诊断方法。在信号分解环节采用VMD算法对各式轴承信号进行分解,并通过退火式选择遗传算法完成对该算法重要参数的寻优。在特征提取和故障识别环节,通过峭度-相关准则选取信号分解后的最佳模态分量,并提取该分量的MFE值作为特征向量输入到PNN诊断模型中完成故障识别。通过结合VMD与PE,FE和MPE的不同特征提取方法的对比试验可得,提出的基于VMD-MFE的特征提取方法在处理电机轴承诊断过程中具有更强的稳定性和更高的准确率。