发掘隐含条件,巧设辅助元素
——初中代数中运用换元法解题的思路与方法探索
刘晓燕
⦿江苏省苏州市吴中区城西中学
在初中代数中,换元法是一种能够灵活运用、十分重要且有效的解题方法.换元法,即变量替换,是把某个代数式看成一个新的未知数(元)来实施替换,其本质还是转化.通过这种转化能够达到“化繁为简、化难为易、化陌生为熟悉、事半功倍”的效果[1].换元法被广泛地应用于解方程(组)、因式分解、代数式变形、化简求值、等式证明等各类数学问题的解答之中,现针对其常见的解题思路与方法作如下探讨.
1 代数式变形后换元
在初中数学中,学生已经学习了方程(组)的最基本的解法,而换元法是其中最方便、快捷且最具优越性的一种解法.它能够把高次降为低次、无理式化为有理式、分式化为整式,将复杂的方程化为简单的、最基本的方程,从而使方程(组)顺利得解.运用换元法解方程(组),关键是观察分析出能够换元的整式或分式,有时需要对方程(组)进行整理变形(如因式分解、配方、添拆项等)才能观察出如何换元[2].
例1解方程:(x+1)(x+3)(x+5)(x+7)+15=0.
解:把原方程变形为(x2+8x+7)(x2+8x+15)+15=0.
设y=x2+8x+11,则原方程为(y-4)(y+4)+15=0,即y2-1=0,解得y1=1,或y2=-1.
所以得到方程x2+8x+11=1,或x2+8x+11=-1.
思路与方法:本题如果按照常规解题思路,即先把左边的括号全部展开,然后再分解,运算非常繁琐.所以需要换个思路,尝试将左边的四个因式分成两组,变成[(x+1)(x+7)][(x+3)(x+5)]+15=0的形式,分别利用整式的乘法展开,再设辅助变量,用换元法求解.
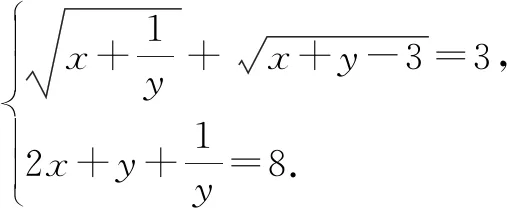

由 [①2-②]÷2,得uv=2.
所以u,v可以看作是方程z2-3z+2=0的两根.因此可得u=1,v=2;或u=2,v=1.
还原得关于x,y的方程组




由此易得原方程组的解为
经检验知,以上四组解都是原方程组的解.

2 利用原代数式换元
在因式分解时,将相同的代数式换元是最常用的方法.当题目中多处出现相同的代数式时,可以把这个代数式设为一个字母(例如a),从而把整个代数式变为关于a的代数式.
例3分解因式:(x2-4x)2-2(x2-4x)-15.
解:设x2-4x=a,则
(x2-4x)2-2(x2-4x)-15
=a2-2a-15
=(a-5)(a+3)
=(x2-4x-5)(x2-4x+3)
=(x-5)(x+1)(x-3)(x-1).
思路与方法:通过观察发现,原代数式中x2-4x出现了多次,将它设为另一个字母后,既可以做到“设元务尽”(不再出现x),又便于继续分解.
例4分解因式:(b+c-a)(c+a-b)(a+b-c)+a(a-b+c)(a+b-c)+b(a+b-c)(-a+b+c)+c(-a+b+c)(a-b+c).
解:设x=b+c-a,y=c+a-b,z=a+b-c,则

思路与方法:凭经验可知,本题如果用整式的乘法展开、整理将会十分繁琐,需另想办法.通过对原式的观察发现,如果利用原代数式换元,设x=b+c-a,y=c+a-b,z=a+b-c,那么x+y+z=a+b+c,y+z=2a,z+x=2b,x+y=2c,再进行代换就会使原式大为简化.从本题的解题过程中,我们可以再次感受到换元法“以一当多、便于观察、简化运算、开阔思路”的巨大优越性.
3 引进辅助元素换元
代数式的恒等变形是解决有关代数式问题的重要手段,当代数式的形式较复杂时,可以尝试运用换元法,通过引进辅助元素使其形式变得简单.




思路与方法:针对题设条件中的连等,引入辅助变量,将三个变量集中在一个变量上,从而简化了运算过程.

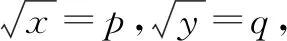

思路与方法:显然,本题如果按照去分母、计算、化简,由左边推出右边的常规方法来证明,将非常困难.但采用引进辅助元素代换的方法,不仅简化了书写,而且更容易发现各量之间的隐含关系,分子与分母不断分解,最终达到简化证明过程的目的.
4 结论
从上述典型例题的思路与方法的分析中可以看出,运用换元法解题具有很强的实用性和灵活性.利用换元法引入辅助元素时,需要根据问题的结构、特点灵活加以运用,只有引元恰当才能使运算过程得到简化;有些问题要经过适当的整理、变形,才便于换元时进一步利用条件中的隐含关系.

