一道三角形中线试题的多角度探究
吴志峰
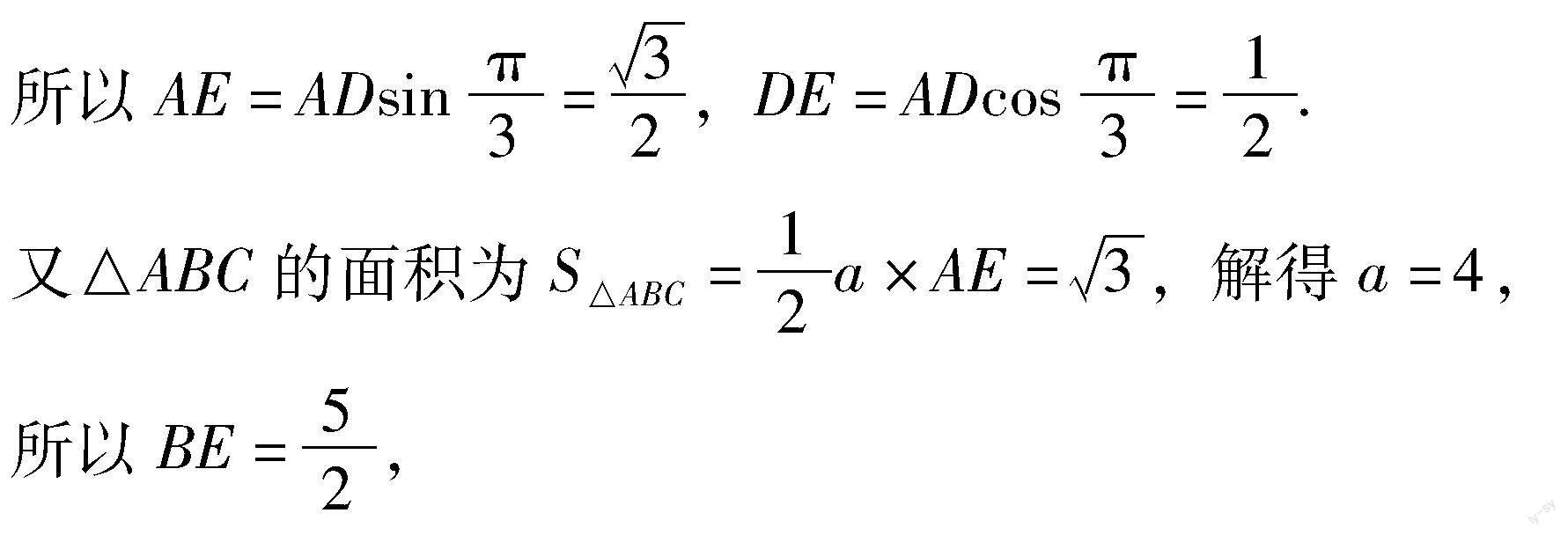
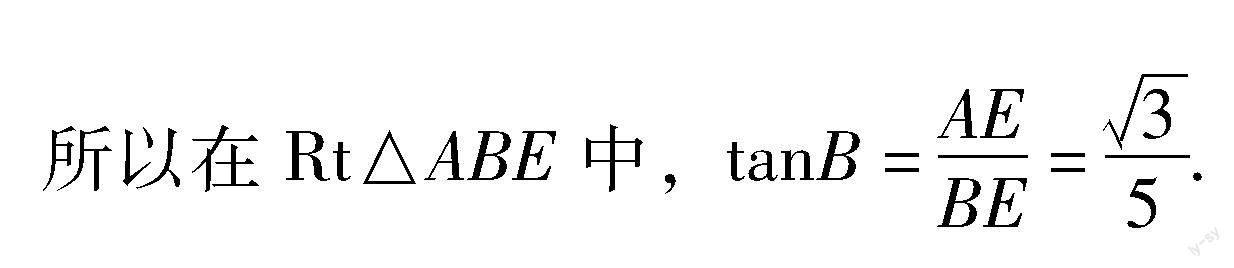
一、真题回放
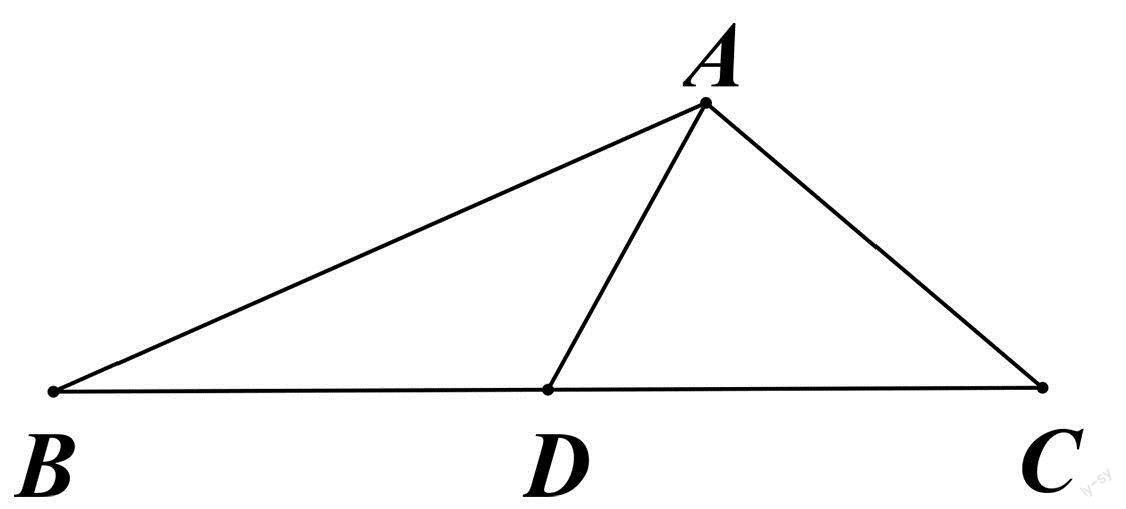
(2023年新高考数学Ⅱ卷第17题)记△ABC的内角A,B,C的对边分别为a,b,c,已知△ABC的面积为3,D为BC中点,且AD=1.
二、试题分析
三、试题解析
第(1)问的求解过程
解法1:利用余弦定理解三角形
解法2:作高法
【评注】在三角形的面积问题中,作高法是一个常见的方法,而且作高的本质也是在构建完全可解的Rt△ADE,而且作高后tanB的值恰好可以在Rt△ABE中利用正切的定义求得,从而使问题得到简化.
第(2)问的求解过程
解法1:利用互补的角构建方程
在△ABD与△ACD中,由余弦定理得:
【评注】本题条件中并没有发现明显的完全可解的三角形,如何利用正余弦定理构建方程组是解题的关键.在本题的几何图形中,有三个三角形,在这类多三角形的几何问题中,往往借助几个三角形的相关联的角(公共角、互补、互余)或公共边来构建方程组.解法1利用了△ABD与△ACD的一对互补的角来构建方程,解法2利用△ABD与△ABC的公共角来构建方程,体现了函数与方程数学思想方法在解题中的应用,这也是利用正、余弦定理解决此类问题的通法.
解法3:利用中线的向量公式
【评注】新教材把解三角形的知识放在了平面向量这一单元中,突出了向量方法在平面几何中的应用,体现了向量的工具性和应用性,也突出了向量法在解三角形问题中的地位.向量法是解三角形问题中的常用方法,向量法在三角形中线问题中有着广泛的应用,利用三角形中线的向量公式或极化恒等式等,通过向量的运算可以快速得到三角形边角之间的联系,为解题提供方便.
解法5:利用中线长公式
在△ABC中,因为D为BC中点,
得a2=2(b2+c2)-4AD2=12,所以a=23.(下同解法1)
【评注】中线长公式来源于人教A版教材必修第二册第六章平面向量及其应用的一道课后习题,在高考解答题中用这个公式需要先进行证明,可以利用余弦定理证明,也可以用向量法证明,上面的解法4、5得到的边的关系就是中线长公式的一个变形.如果能够熟练掌握这个公式,在求解三角形中线的问题中可以事半功倍.
解法6:补形后再解三角形
△ABF中,由余弦定理得:AF2=b2+c2-2bccos∠ABF,
所以2bccos∠ABF=b2+c2-AF2=8-4=4,
所以bc=4,联立b2+c2=8解得b=c=2.
【评注】此解法通过补形,借助平面几何中全等三角形的知识,把问题转化成解△ABF的问题,从而把一个多三角形的问题转化成了单个三角形的求解问题.通过图形转化,使条件更简洁和便于運算,体现了数形结合思想在解题中的应用.这也是解决三角形中线相关问题一种常用的解题思路.
解法7:坐标法
如图,以BC所在直线为x轴,以BC的垂直平分线为y轴建立平面直角坐标系,
设A(x,y),B(-t,0),C(t,0),t>0.
由AD=1得x2+y2=1.
由b2+c2=8得(x-t)2+y2+(x+t)2+y2=8,
【评注】坐标法是解决几何问题的常用解法之一,通过引入坐标系,借助坐标来表示平面几何中的边和角,再进行求解的过程.解三角形问题本身就是一个几何问题,当我们用正余弦定理求解遇到困难时,不妨试试坐标法.
四、解题反思
“横看成岭侧成峰,远近高低各不同”,我们从不同角度对这个高考题进行求解,特别是对第(2)问的解析中,更是有多种构建方程的思路和方法,解法1、2利用正余弦定理构建方程,解法3、4利用向量构建方程,这两个解法是解决解三角形问题的通法,突出考查函数与方程数学思想方法的应用,要求考生能够熟练掌握.解法6、7从几何角度进行求解,巧妙借助平面几何的知识和解析法,使问题得到简化,是解决解三角形问题的特殊解法。了解这些解法有助于同学们了解知识之间的联系,对提升解题能力,提升数学核心素养有很大的帮助.通过以上分析,我们发现,在解决三角形的中线及其相关问题时,以下几个常用的公式给解题带来很大帮助,我们需要牢记.
五、练习题
下面整理几道与三角形中线有关的练习,从求边长、求角度、求面积、求最值、求范围五方面进行整理,供各位考生参考.
1.求边长
2.求角
练习2.在△ABC中,内角A,B,C所对的边分别为a,b,c.已知b2=ac,点D为AC中点,BD=b,求cos∠ABC.
【简析】由中线长公式得4BD2=4b2=2a2+2c2-b2,
又b2=ac,所以2a2+2c2-5ac=0,
解得a=2c或c=2a,
3.求面积
【简析】
设BD=DC=t,t>0,
△ABD中,AB2=AD2+BD2-2AD·BDcos∠ADB=4+t2+2t,
△ACD中,AC2=AD2+CD2-2AD·CDcos∠ADC=4+t2-2t,
5.求范围
【简析】
——书写要点(三)

