二维双层准地转方程的高阶衰减估计
李慧玲,张景军
(1.长沙理工大学 数学与统计学院,湖南长沙 410114;2.嘉兴学院 数据科学学院,浙江嘉兴 314001)
0 引言
本文主要研究如下带有耗散项和摩擦项的准地转方程:
(1)
(2)
(ψ1(x,y,0),ψ2(x,y,0))=(ψ10,ψ20),
(3)
其中ψ1(x,y,t)和ψ2(x,y,t)分别表示描述顶层运动和底层运动的流函数,雅可比算子J定义为J(f,g)=fxgy-fygx,其中F、Re、μ和β分别表示旋转弗劳德数、雷诺数、摩擦系数和科里奥利力数,δ表示上层流和下层流的厚度之比.
双层准地转模型是描述单层正压流运动的二维准地转模型和描述连续分层斜压流运动的三维准地转模型之间的中间模型,在海洋学、大气科学和天体物理学中具有广泛的应用,关于上述相关方程的推导可参考文献[1-4].文献[5]发现,一类标量型2D准地转方程与3D欧拉方程具有高度的相似性,因此这类方程在过去十几年时间里被广泛研究.
文献[6]研究了方程(1)、方程(2)及方程(3)的弱解的存在性和解的衰减估计.文献[7]系统地研究了分数阶双层准地转模型弱解和光滑解的存在性及解的长时间性态等问题.特别是利用Fourier分裂法,文献[6]中得到了两个衰减估计如下:

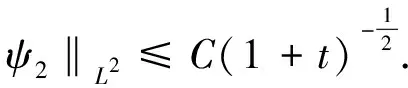

本文的主要结果如下:
定理1:设初值(ψ10,ψ20)∈L1(2)∩H6(2),则方程(1)-(3)存在唯一的整体光滑解(ψ1,ψ2),且满足衰减估计‖Δψ1‖L2+‖Δψ2‖L2+‖∇ψ1-∇ψ2‖L2≤C(1+t)-1,其中常数C与初值范数和方程中的物理系数有关.
定理1中的存在性部分本质上可用文献[7]中的方法获得,此处略去这部分的证明.此外,利用本文的方法,实际上还可以得到更高阶导数的衰减估计,因推导过程类似并限于篇幅,本文省略了这部分内容.以下主要证明定理1中的衰减估计.
1 预备知识
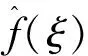
引理1:设ψ∈H3(2),ψ1,ψ2∈H1(2),则雅可比算子J满足


引理2:设初值(ψ10,ψ20)∈L1(2)∩H6(2),则方程(1)-(3)的解(ψ1,ψ2)满足
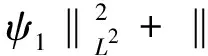
引理1的第一个估计见文献[8],引理1的第二个估计和引理2见文献[6].
引理3:设初值(ψ10,ψ20)∈L1(2)∩H6(2),则方程(1)-(3)的解(ψ1,ψ2)满足
证明:对方程(1)和(2)进行傅里叶变换,得到
(4)
(5)
一方面,将式(4)乘以δ加上式(5),可以得到
(6)
另一方面,将式(4)减去式(5),又可得
(7)
根据式(6)和式(7),再利用引理1和引理2中的估计,有


证毕.
注意到,文献[6]中得到的估计为
由此可见,引理3将关于时间的幂次方增长改进到了对数形式的增长.
2 定理1的证明
利用性质J(f,f)=0,计算(1)×2δΔψ1+(2)×2Δψ2后再积分,可得到
2δF∬[J(ψ1,ψ1-ψ2)Δψ1-J(ψ2,ψ1-ψ2)Δψ2]dxdy.
(8)
利用分部积分和插值不等式,有
2δF|∬[J(ψ1,ψ1-ψ2)Δψ1-J(ψ2,ψ1-ψ2)Δψ2]dxdy|≤
C‖∇ψ1‖L∞‖∇Δψ1‖L2‖ψ1-ψ2‖L2+C‖∇ψ2‖L∞‖∇Δψ2‖L2‖ψ1-ψ2‖L2≤
(9)
将式(9)代入式(8)中,并利用引理2,得到
(10)
利用傅里叶变换,式(10)等价于
(11)
(12)
将式(12)代入式(11),有
(13)
根据引理3和集合S(t)的定义,式(13)右边的积分项有如下估计
(14)
结合式(13)和式(14),得


根据常数c0和c1的定义,有

上式关于时间积分可得
∬(δ|Δψ1|2+|Δψ2|2+2δF|∇(ψ1-ψ2)|2)dxdy≤C(1+t)-2.
证毕.
定理1的证明主要是基于Schonbek的Fourier分裂技术[9],文献[10]对该方法作了改进并得到了相关模型的最优衰减估计.

