分形Cauchy空间到Zygmund型空间的积分型复合算子

艾 钱

(浙江师范大学 数学与计算机科学学院，浙江金华 321004)

0 引言

(0.1)

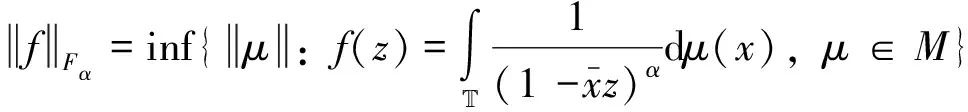
近年来，分形Cauchy空间Fα在复合算子、求导算子和积分算子中有广泛研究.[1-8]特别地，分形Cauchy空间与规范化单叶函数空间E有密切的关系，对α>2，成立E⊆Fα[9].

设β>0，Bloch型空间Bβ定义为全体f∈H()满足

Zygmund型空间Zβ定义为全体f∈H()满足

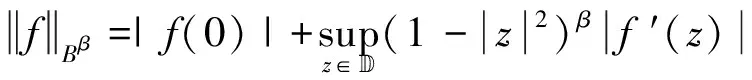
设φ∈S，定义H()上的由φ导出的复合算子Cφ为

Cφf(z)=f(φ(z))，f∈H().

对g∈H()，由g导出的Volterra型积分算子定义如下：

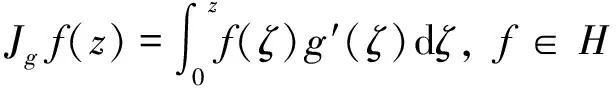
当g(z)=-log(1-z)时，算子Jg与Cesàro算子一致. 另一个由g导出的积分算子Ig定义如下：

由g∈H()导出的乘子算子Mg定义为Mgf(z)=g(z)f(z)，其与积分算子Jg和Ig满足下面的关系：

Jgf+Igf+f(0)g(0)=Mgf.

近40年来，对在不同背景(空间)下的复合算子有了广泛的研究. 经典文献[10]和[11]系统研究了复合算子在解析函数空间的基本理论性质，特别地，对算子理论性质和诱导该算子的函数性质之间的研究尤为深刻. 基于文献[12]对Volterra型算子在解析函数空间中的工作(Volterra型算子在Hardy空间H2中有界当且仅当g∈BMOA等)，对积分算子Jg和Ig在不同函数空间中相继有了广泛的研究，Aleman和Siskakis研究了Hardy空间和Bergman空间上积分算子的有界性和紧性.[13-14]

随着算子理论研究的不断深入，很多学者考虑不同解析函数空间上两个(类)算子的乘积，复合算子与积分算子的乘积在不同函数空间的性质成为近年来研究的热点. Li和Stevic研究了几类不同解析函数空间上复合算子与积分算子乘积的有界性和紧性；[15-17]Hibschweiler研究了从分形Cauchy空间到Bloch型空间复合算子与求导算子乘积的有界性和紧性.[18]引用文献[15-18]中证明所用到的工具和方法，本文考虑分形Cauchy空间到Zygmund型空间复合算子与两类积分算子的乘积

并给出刻画以上乘积算子有界或成为紧的充分条件和必要条件.

1 预备引理

本节，我们回顾一些基本知识和预备引理.

文献[19]中，紧算子的定义如下：

函数空间中算子的紧性有很多等价的条件，根据文献[11]中的定理1.3.3，我们给出积分算子JgCφ(CφJg，IgCφ，CφIg)：Fα→Zβ紧的充要条件.

引理1 设α，β>0，φ∈S，g∈H()，令算子T=JgCφ，CφJg，IgCφ或CφIg. 则算子T：Fα→Zβ是紧的当且仅当对任意Fα中在的紧子集一致收敛于0的有界函数列{fn}(n→∞)，当n→∞时

文献[20]中，Shapiro给出了复合算子紧的必要条件.

文献[21]给出了复合算子在Bloch型空间中有界和紧的等价条件.

引理3 设α，β>0，φ∈S，则下列结论成立：

(1)算子Cφ：Bα→Bβ有界当且仅当

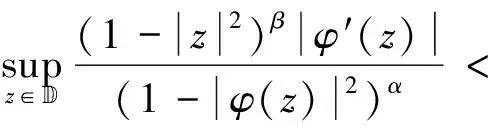
(1.1)

(2)算子Cφ：Bα→Bβ是紧的当且仅当φ∈Bβ且

(1.2)

根据关系式(0.1)，Hibschweiler[9]证明对每个w∈，有且下面的结论成立.

引理4 设α>0，对函数f∈Fα和非负整数n，存在一个与f无关的正常数C使得

(1.3)

引理5[22]设α>0，固定w∈，对任意的非负整数n定义

(1.4)

在本文中，记XY表示存在一个正常数C使得X≤CY.

2 主要结果

2.1 算子JgCφ(CφJg)：Fα→Zβ

本节，我们刻画从分形Cauchy空间到Zygmund型空间的积分型复合算子JgCφ和CφJg的有界性和紧性.

首先，令g=φ，利用引理3对算子JφCφ：Fα→Zβ(0<β<1)的有界性和紧性进行刻画.

定理1 设φ∈S，对α>0和0<β<1，下列结论相互等价：

(1)JφCφ：Fα→Zβ是有界的；

(2)JφCφ：Fα→Zβ是紧的；

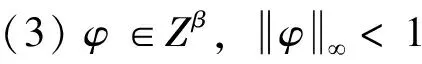
证明：(2)⟹(1)是显然的.

(1)⟹(3)：假设JφCφ：Fα→Zβ有界，则存在一个常数C，对所有的f∈Fα，有

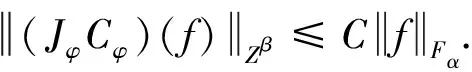
(2.1)

(2.2)

因此，有φ∈Zβ，根据式(2.1)和式(2.2)，又有

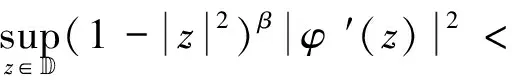
(2.3)

即φ∈Bβ/2.

对固定的w∈，定义函数

(2.4)

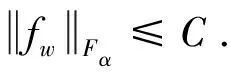
(2.5)

将式(2.5)中的z用w代替，得

(2.6)

因此，有

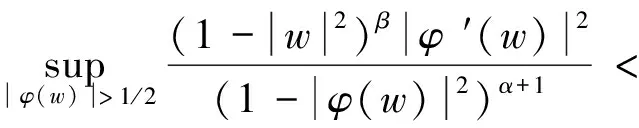
(2.7)

再由式(2.3)，有

(2.8)

根据式(2.7)和式(2.8)，有

(2.9)

因此，可以得到

结合上式和引理3的条件(1)可知：Cφ：Bβ/2→Bβ/2有界.

进一步，通过式(2.9)知，当|φ(w)|→1时，有

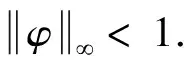
根据引理1，设{fn}为Fα中有界且当n→∞时在的紧子集中一致收敛于0的函数列. 只需证明当n→∞时，有

注意到|(JφCφfn)(0)|=0，又n→∞时{fn}在的紧子集一致收敛于0，所以，当n→∞时，有|(JφCφfn)′(0)|=|fn(φ(0))φ′(0)|→0. 根据式(2.3)，对z∈有

(1-|z|2)β|(JφCφfn)″(z)|=

(1-|z|2)β|fn′(φ(z))(φ′(z))2+fn(φ(z))φ″(z)|

由于{fn′}当n→∞时在的紧子集一致收敛于0，有

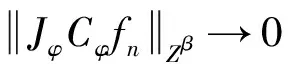
根据定理1及证明，有下面的结论.

推论1 设α，β>0，φ∈S，若α+1>β，则下列的结论相互等价：

(1)JφCφ：Fα→Zβ是有界的；

(2)JφCφ：Fα→Zβ是紧的；

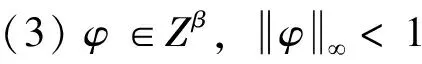
对任意g∈H()，利用符号φ和g刻画乘积算子JgCφ：Fα→Zβ的有界性和紧性.

定理2 设α，β>0，φ∈S，g∈H()，则下面的结论成立.

(1)算子JgCφ：Fα→Zβ有界当且仅当

(2.10)

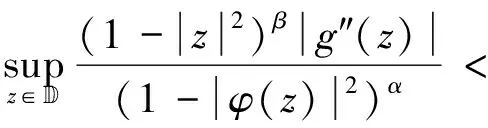
(2.11)

(2)若算子JgCφ：Fα→Zβ有界，则算子JgCφ：Fα→Zβ为紧的当且仅当

(2.12)

(2.13)

证明：(1)充分性. 假设式(2.10)和式(2.11)成立，对任意f∈Fα，根据式(2.10)和引理4，有

(2.14)

同理，根据式(2.11)和引理4，有

(2.15)

结合式(2.14)和式(2.15)，有

必要性. 假设算子JgCφ：Fα→Zβ有界.定理1中(1)⟹(3)的证明相同，再次利用测试函数f(z)=1，z∈Fα和算子JgCφ：Fα→Zβ的有界性可知：

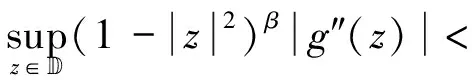
(2.16)

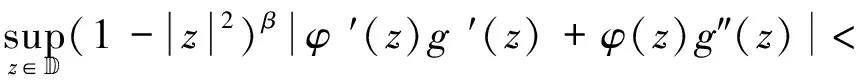
(2.17)

根据式(2.16)和式(2.17)，有

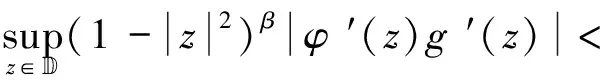
(2.18)

因此，有

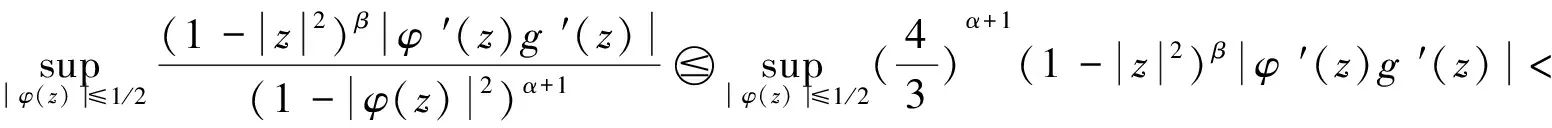
(2.19)

利用算子JgCφ：Fα→Zβ的有界性和定理1证明中的式(2.4)定义的函数fw(z)∈Fα，可得：

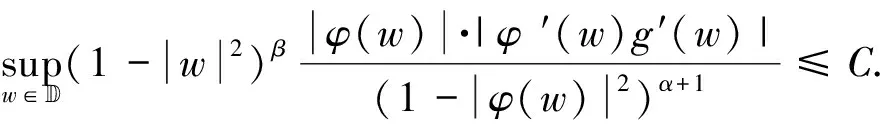
(2.20)

结合式(2.19)和式(2.20)可知，式(2.10)成立.

对每个w∈，定义函数

(2.21)

通过简单计算，可知：

因此，将式(2.21)中的z用w代替，得

(2.22)

因此，式(2.11)成立，(1)证明完毕.

(2)充分性. 假设算子JgCφ：Fα→Zβ有界且式(2.12)和式(2.13)成立，要证算子JgCφ：Fα→Zβ为紧的. 根据引理1，设{fn}为Fα中有界且当n→∞时在的紧子集中一致收敛于0的函数列，只需证明当n→∞时，

根据引理4，存在仅与α有关的正常数C，使对n=1，2，…，和z∈，有

由上式和式(2.12)知，对任意给定ε>0，存在一个r0∈(0，1)，使得

(2.23)

由算子JgCφ：Fα→Zβ的有界性知式(2.18)成立. 因此，有

(1-|z|2)β|fn′(φ(z))φ′(z)g′(z)||fn′(φ(z))|.

又因为{fn′}在的紧子集一致收敛于0，因此，存在N>0，使得当n>N时，有

(2.24)

由式(2.23)和式(2.24)，当n>N时，有

(2.25)

同理，根据式(2.13)和算子JgCφ：Fα→Zβ的有界性(式(2.16)成立)可知，存在N1>0，使得当n>N1时，有

(2.26)

由式(2.25)和式(2.26)，可得

(2.27)

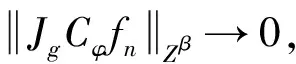
必要性. 假设算子JgCφ：Fα→Zβ是紧的，自然地，算子JgCφ：Fα→Zβ有界，证明式(2.12)和式(2.13)成立.

(2.28)

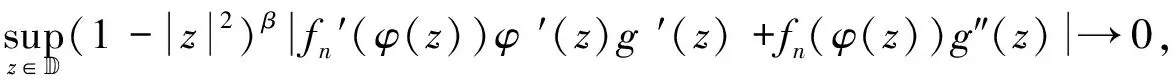
(2.29)

将上述结果带入式(2.29)，有

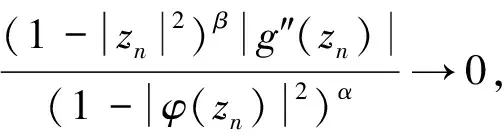
又|φ(zn)|→1，(n→∞)，因此，式(2.12)成立.

同理，定义Fα中的函数如下：

根据算子JgCφ：Fα→Zβ的紧性可得式(2.12)成立，(2)证明完毕.

推论2 设α，β>0，φ∈S，g∈H()，若则下列的结论相互等价：

(1)JgCφ：Fα→Zβ是有界的；

(2)JgCφ：Fα→Zβ是紧的；

对于算子CφJφ：Fα→Zβ(g=φ时)，不能得到与定理1类似的结论.

接下来，对乘积算子CφJg：Fα→Zβ的有界性和紧性进行刻画.

定理3 设α，β>0，φ∈S，g∈H()，则下列结论成立.

(1)算子CφJg：Fα→Zβ有界当且仅当

(2.30)

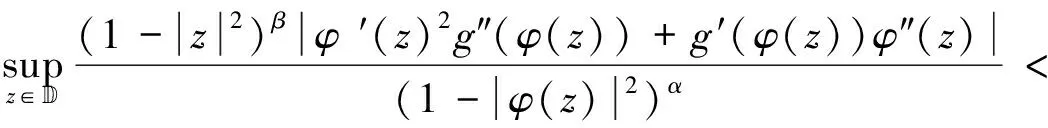
(2.31)

(2)若算子CφJg：Fα→Zβ有界，则算子CφJg：Fα→Zβ为紧的当且仅当

(2.32)

(2.33)

证明：(1)充分性. 假设式(2.30)和式(2.31)成立，对任意f∈Fα，根据引理4

(2.34)

和

(2.35)

必要性. 假设算子CφJg：Fα→Zβ有界，与定理2相同，使用测试函数f(z)=1，z∈Fα，由算子CφJg：Fα→Zβ的有界性可得

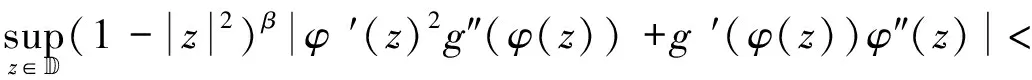
(2.36)

(2.37)

结合式(2.36)和式(2.37)，得

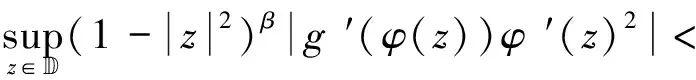
(2.38)

根据式(2.38)，可得

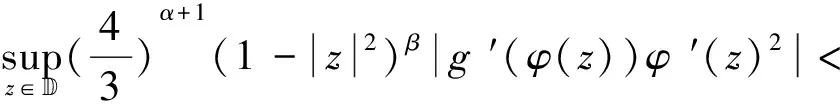
(2.39)

利用算子CφJg：Fα→Zβ的有界性和定理1、定理2的证明所定义的函数fw，hw∈Fα，有

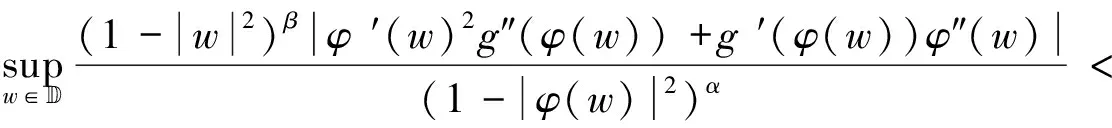
(2.40)

和

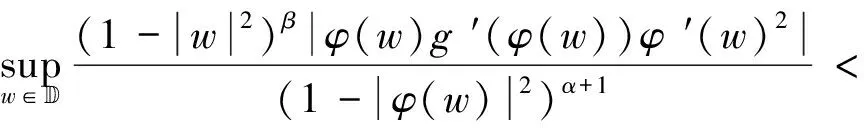
(2.41)

根据式(2.40)可知，式(2.31)成立，根据(2.41)，有

(2.42)

根据式(2.39)和式(2.42)可知，式(2.30)成立，(1)证明完毕.

(2)充分性. 假设算子CφJg：Fα→Zβ有界且式(2.32)和式(2.33)成立，根据引理1，设{fn}为Fα中有界且当n→∞时在的紧子集中一致收敛于0的函数列，只需证明(n→∞)即可.

根据引理4，存在仅与α有关的正常数C，使得对n=1，2，…，和z∈，有

由上式和式(2.33)知，对任意给定ε>0，存在一个r0∈(0，1)，使得

(2.43)

由算子CφJg：Fα→Zβ的有界性可知，式(2.38)成立，因此，有

(1-|z|2)β|fn′(φ(z))g′(φ(z))φ′(z)2||fn′(φ(z))|.

又因为{fn′}在的紧子集一致收敛于0，因此，存在N>0，使得当n>N时，有

(2.44)

由式(2.43)和式(2.44)可知，当n>N时，有

(2.45)

同理，由式(2.32)可知，存在N1>0，使得当n>N1时，有

(2.46)

根据式(2.45)和式(2.46)，有

(2.47)

同理，当n→∞时，|CφJgfn(0)|→0，|CφJgfn′(0)|→0.

必要性. 假设算子CφJg：Fα→Zβ是紧的. 由定理2证明中定义的函数fn和hn，可知

由引理5可知，fn、hn∈Fα且fn、hn在的紧子集中一致收敛于0，且

(2.48)

(2.49)

根据定理2中(2)的证明，结合式(2.48)和式(2.49)，根据引理1及算子CφJg：Fα→Zβ的紧性，可知式(2.32)和式(2.33)成立，证毕.

推论3 设α，β>0，φ∈S，g∈H()，若则下列的结论相互等价：

(1)CφJg：Fα→Zβ是有界的；

(2)CφJg：Fα→Zβ是紧的；

(2.50)

2.2 算子IgCφ(CφIg)：Fα→Zβ

本节，刻画分形Cauchy空间到Zygmund型空间的积分型算子IgCφ和CφIg的有界性和紧性. 与定理1相同，当g=φ时，利用引理3对算子IφCφ：Fα→Zβ(0<β<1)的有界性和紧性进行刻画.

定理4 设φ∈S，对α>0和0<β<1，下列的结论相互等价：

(1)IφCφ：Fα→Zβ是有界的；

(2)IφCφ：Fα→Zβ是紧的；

证明：(2)⟹(1)是显然的.

(2.51)

即φ∈Bβ，且

(2.52)

对固定的w∈，定义函数

(2.53)

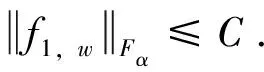
(2.54)

将式(2.54)中的z用w代替，得

(2.55)

因此，有

(2.56)

结合式(2.52)和式(2.56)，有

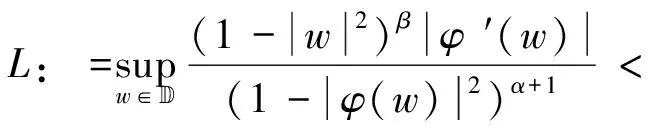
(2.57)

因此，可以得到

结合上式和引理3中的(1)可知，Cφ：Bβ→Bβ有界. 进一步，通过式(2.57)可知，当|φ(w)|→1时，有

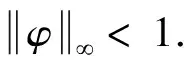
同理，根据引理1，设{fn}为Fα中有界且当n→∞时在的紧子集中一致收敛于0的函数列. 只需证明当n→∞时，有

注意到|IφCφfn(0)|=0和当n→∞时，有|(IφCφfn)′(0)|→0. 根据式(2.51)，对z∈，有

(1-|z|2)β|(IφCφfn)″(z)|=

(1-|z|2)β|fn″(φ(z))φ(z)φ′(z)+fn′(φ(z))φ′(z)|

由于{fn′}，{fn″}当n→∞时在的紧子集一致收敛于0，故有

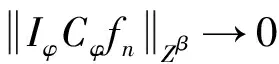
根据定理4的证明，有下面的结论.

推论4 设α，β>0，φ∈S，若α+1>β，则下列的结论相互等价：

(1)IφCφ：Fα→Zβ是有界的；

(2)IφCφ：Fα→Zβ是紧的；

定理5 设α，β>0，φ∈S，g∈H()，则下列结论成立.

(1)算子IgCφ：Fα→Zβ有界当且仅当

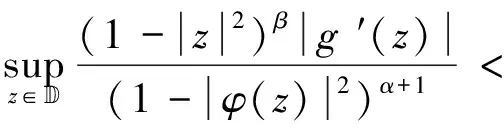
(2.58)

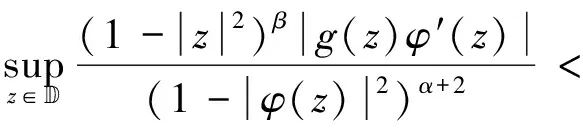
(2.59)

(2)若算子IgCφ：Fα→Zβ有界，则算子IgCφ：Fα→Zβ为紧的当且仅当

(2.60)

(2.61)

证明：(1)充分性. 假设式(2.58)和式(2.59)成立，对任意f∈Fα，根据式(2.58)和引理4，有

(2.62)

同理，根据式(2.59)和引理4，有

(2.63)

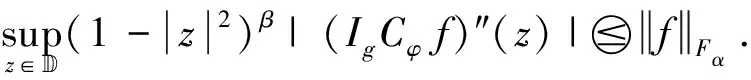
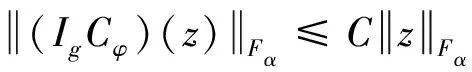
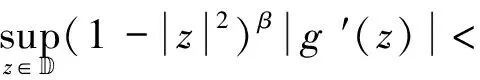
(2.64)

(2.65)

根据式(2.64)和式(2.65)，有

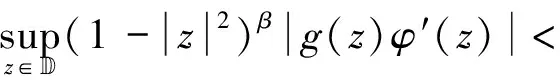
(2.66)

根据式(2.64)和式(2.66)，有

(2.67)

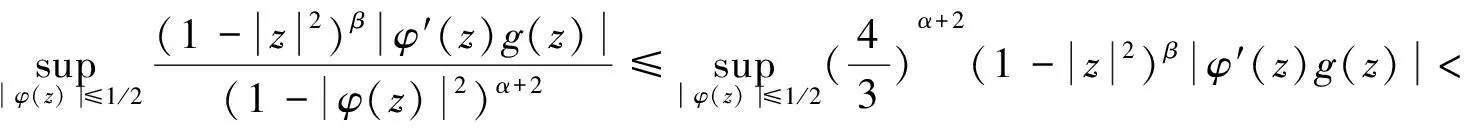
(2.68)

利用算子IgCφ：Fα→Zβ的有界性和定理4证明中的式(2.53)定义的函数f1，w(z)∈Fα，可得

则有

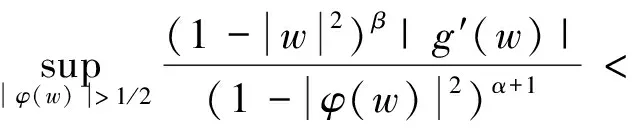
(2.69)

根据式(2.67)和式(2.69)可知，式(2.58)成立.

对每个w∈，定义函数

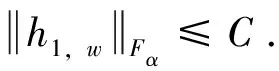
(2.70)

因此，将式(2.70)中的z用w代替，得

因此，有

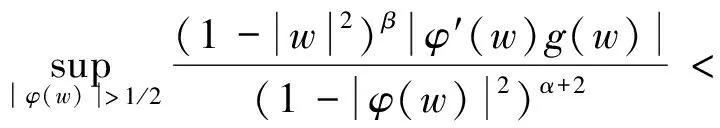
(2.71)

根据式(2.68)和式(2.71)可知，式(2.59)成立，(1)证明完毕.

(2)充分性. 假设算子IgCφ：Fα→Zβ有界且式(2.60)和式(2.61)成立，要证明算子IgCφ：Fα→Zβ为紧的，根据引理1，设{fn}为Fα中有界且当n→∞时在的紧子集中一致收敛于0的函数列，只需证明当n→∞时

根据引理4，存在仅与α有关的正常数C，使得对n=1，2，…，和z∈，有

由上式和式(2.60)可知，对任意给定的ε>0，存在一个r0∈(0，1)，使得

(2.72)

由算子IgCφ：Fα→Zβ的有界性可知，式(2.64)成立. 因此，有

(1-|z|2)β|fn′(φ(z))g′(z)||fn′(φ(z))|.

又因为{fn′}在的紧子集一致收敛于0，因此，存在N>0，使得当n>N时，有

(2.73)

由式(2.72)和式(2.73)，当n>N时，有

(2.74)

同理，根据算子IgCφ：Fα→Zβ的有界性可知，式(2.66)成立，再由式(2.61)可知，存在N1>0，使得当n>N1时，有

(2.75)

根据式(2.74)和式(2.75)

(2.76)

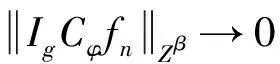
(2.77)

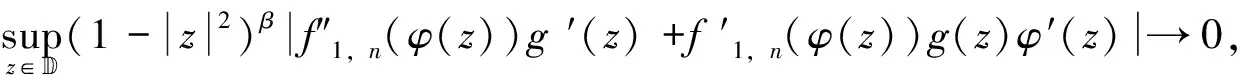
(2.78)

带入式(2.78)，有

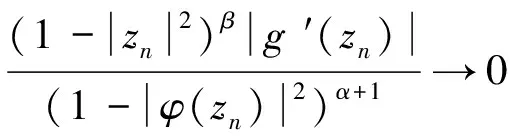
(2.79)

又|φ(zn)|→1，(n→∞)，根据式(2.79)，即可得证式(2.60).

定义函数

推论5 设α，β>0，φ∈S，g∈H()，若则下列的结论相互等价：

(1)IgCφ：Fα→Zβ是有界的；

(2)IgCφ：Fα→Zβ是紧的；

定理6 设α，β>0，φ∈S，g∈H()，则下列结论成立.

(1)算子CφIg：Fα→Zβ有界当且仅当

(2.80)

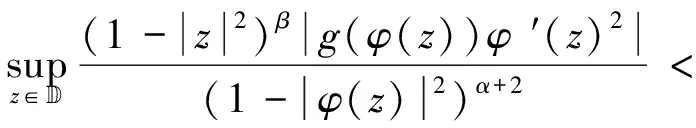
(2.81)

(2)若算子CφIg：Fα→Zβ有界，则算子CφIg：Fα→Zβ为紧的当且仅当

(2.82)

(2.83)

证明：(1)充分性. 假设式(2.80)和式(2.81)成立，对任意f∈Fα，根据引理4、式(2.80)和式(2.81)，存在正常数C，使得

(2.84)

(2.85)

必要性. 假设算子CφIg：Fα→Zβ有界，使用测试函数f(z)=z，z2/2∈Fα，由算子CφIg：Fα→Zβ的有界性，可得

(2.86)

(2.87)

根据式(2.86)和式(2.87)，可得

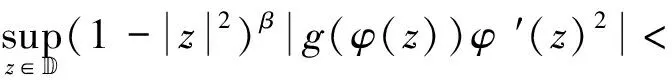
(2.88)

根据式(2.86)和式(2.88)，可得

(2.89)

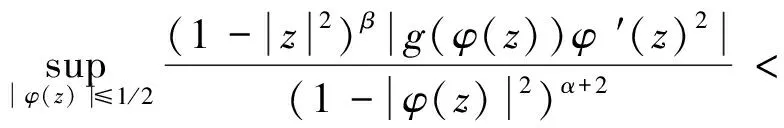
(2.90)

根据定理4、定理5的证明所定义的函数f1，w，h1，w∈Fα，利用算子CφIg：Fα→Zβ的有界性，有

(2.91)

(2.92)

根据式(2.91)和式(2.92)，有

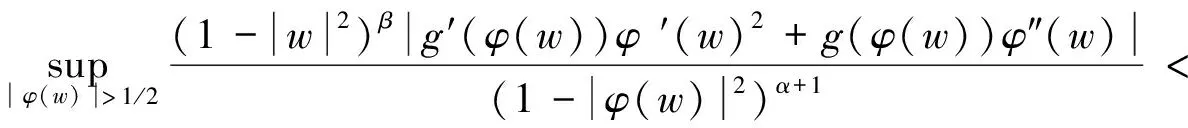
(2.93)

(2.94)

结合式(2.89)、式(2.90)、式(2.93)和式(2.94)可知，式(2.80)、式(2.81)成立.

(2)充分性. 根据引理1，使用与定理5中(2)的证明相同的方法可直接得到.

必要性. 根据定理5的证明及其定义的函数f1，n，h1，n∈Fα，再由引理1和算子CφIg：Fα→Zβ的紧性，可知式(2.82)和式(2.83)成立，证明完毕.

推论6 设α，β>0，φ∈S，g∈H()，若则下列的结论相互等价：

(1)CφIg：Fα→Zβ是有界的；

(2)CφIg：Fα→Zβ是紧的；

致谢：衷心感谢导师胡俊云教授对论文的悉心指导！