分形Cauchy空间到Bloch型空间的复合算子与微分算子乘积的范数估计

祁燕茹

(浙江师范大学 数学与计算机科学学院，浙江金华 321004)

0 引言

设X和Y是Banach空间，有界线性算子T：X→Y的本性范数是它与将X映射为Y的紧算子集K的距离，即：

其中‖‖X→Y为算子范数.

(1)

构成，其中f∈H()，μ∈M.空间Fα关于范数

(2)

为Banach空间，其中μ∈M为满足式(1)的所有复Borel测度.当α=1时，称F1为Cauchy积分变换空间.分形Cauchy空间与规范化单叶函数空间S有密切的联系，且对α>2，有E⊆Fα成立.[2]近年来，学者在一般分形Cauchy空间Fα上就复合算子、微分算子和乘积算子及其算子差分中有广泛研究.[12-14]

设β>0，Bloch型空间Bβ为上使∞成立的解析函数全体构成，且关于范数为Banach空间.小β-Bloch空间为Bβ的子空间，由所有f∈H()，且使得成立的函数全体组成.B1为Bloch空间，记为B.关于Bloch空间的更多内容及定理见文献[15].

DCφf(z)=φ′(z)f′(φ(z)) ，CφDf(z)=f′(φ(z)).

显然，算子DCφ、CφD为复合算子Cφ和微分算子D的推广.微分算子D在很多熟悉的全纯函数空间上通常是无界的.具体算子(如复合算子、乘法算子、加权复合算子、Toeplitz算子和Hankel算子)的一个主要问题是将算子理论性质与函数理论性质联系起来.

对任意φ∈S()，由Schwarz-Pick引理，得到算子Cφ在Bloch空间上有界.1995年，Madigan和Matheson证明了Cφ：B→B紧当且仅当年，Montes-Rodrieguez得到了Cφ：B→B的本性范数的确切值

近年来，人们对单位圆盘上的一些全纯函数空间上的乘积型算子越来越关注.文献[11]首次刻画了Bergman空间和Hardy空间之间算子DCφ的有界性和紧性.文献[28]研究了加权函数空间和Bloch空间到Zygmund空间算子DCφ的有界性和紧性.文献[29]考虑了Hardy空间H2上算子CφD的有界性和紧性.Ohno对Bloch空间以及小Bloch上的复合算子与微分算子的乘积DCφ和算子CφD的有界性和紧性进行了刻画，相关结果参见文献[9].文献[10]考虑了作用于加权Bergman空间和Bloch型空间之间的算子DCφ和CφD.最近，文献[4]对于算子DCφ和算子CφD在分形Cauchy空间Fα和Bloch型空间Bβ中进行研究，对DCφ：Fα→Bβ和CφD：Fα→Bβ有界性和紧性给出了一些充分必要条件，相关结果如定理1、定理2所示.

定理1 固定α>0，且假设β≥2.设φ∈S()，假设DCφ：Fα→Bβ有界，则下列陈述等价：

(1)DCφ：Fα→Bβ紧；

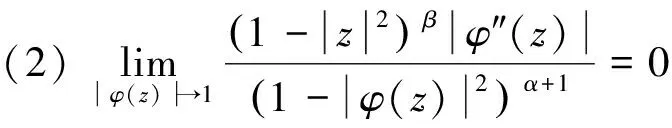
定理2 固定α>0，且假设β≥1.设φ∈S()，假设CφD：Fα→Bβ有界，则下列陈述等价：

(1)CφD：Fα→Bβ紧；

对于算子的本性范数估计，学者在文献[24-26]中给出了新的估计方法，并利用加权复合算子在加权函数空间的相关结论给出算子有界性、紧性以及本性范数的新的刻画.

受定理1、定理2以及上述方法启发，本文的目的是对算子DCφ：Fα→Bβ、CφD：Fα→Bβ的本性范数进行估计.此外，对于算子DCφ：Fα→Bβ及CφD：Fα→Bβ的有界性、紧性和本性范数，我们在文中给出了一个新的刻画.

在本文中，关系a≈b意为ab且ba，即存在正整数C1和C2，使得a≤C1b且b≤C2a.

1 预备知识

后续讨论所需的基本知识和相关引理均在相关文献中给出并证明.

对每个w∈，有成立.[2]

引理1[2]固定α>0，对固定的z∈，f∈Fα和非负整数n，由关系式(1)知，存在一个与f无关的正常数C(只与n有关)，使得

(3)

引理2[1]设α>0，固定w∈，对任意的非负整数n，定义

(4)

则有fw(z)∈Fα，且对所有的w∈，存在一常数C，使得

引理3[1]设α>0，固定w∈，对任意的非负整数n，定义

(5)

则有gw(z)∈Fα，且对所有的w∈，存在一常数C，使得

引理2和引理3将用于构造Fα中的测试函数，证明见文献[6].

引理4[5]设X，Y为单位圆盘上解析函数组成的Banach空间，假设：

(1)Y上的点值泛函连续；

(2)在紧集一致收敛拓扑中，X的闭单位球是X的紧子集；

(3)当X和Y给定紧集上一致收敛的拓扑时，T：X→Y是连续的；

则T为一紧算子当且仅当给定X中一有界序列{fn}，使得在紧集上有fn一致收敛到0，则在Y范数下，序列{Tfn}收敛到0.

2 DCφ：Fα→Bβ的本性范数

在本节，我们就分形Cauchy空间到Bloch型空间的复合算子Cφ与微分算子乘积DCφ的本性范数给出估计.

令a∈，定义；.

定理3 固定α>0，且假设β≥2.设φ∈S()，假设DCφ：Fα→Bβ有界，则

(6)

由于DCφ：Fα→Bβ有界，有

因此，由本性范数的定义，得：

即式(6)成立.

接下来，证明

(7)

成立.设{zj}j∈为中一序列，当j→∞时，使|φ(zj)|→1.定义

由引理可知，kj、lj均属于空间Fα，且均在的紧子集上一致收敛到0.此外，有以及成立，而对任意紧算子K：Fα→Bβ，有：

以及

由本性范数定义，又有

以及

现在，证明

(8)

对r∈[0，1)，设Kr：H()→H()有如下定义

(Krf)(z)=fr(z)=f(rz)，f∈H().

很显然，当r→1时，在的紧子集上有fr一致收敛到f.此外，算子Kr在空间Fα上紧，且有设{rj}⊂(0，1)为一序列，且当j→∞时，有rj→1成立.对正整数j，算子DCφKrj：Fα→Bβ紧.由本性范数定义，有

(9)

为了证明式(8)成立，仅需证明

(10)

和

(11)

(12)

很显然，有：

(13)

现在，考虑

(14)

其中N∈足够大，使对所有j≥N，有且

由于DCφ：Fα→Bβ有界，由文献[4]中的定理3，我们有

(15)

当j→∞时，在的紧子集上，rjfrj′一致收敛到f′，则有

(16)

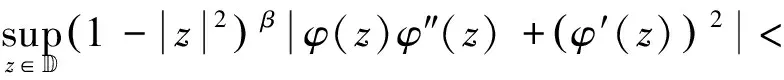
结合式(14)，得

(17)

同样，当j→∞时，在的紧子集上有rj2frj″一致收敛到f″，故有

(18)

对上式取极限N→∞，得

因此，

(19)

对上式取极限N→∞，得

因此，

(20)

由式(12)～式(20)，可得

(21)

3 CφD：Fα→Bβ的本性范数

在本节，对分形Cauchy空间到Bloch型空间的复合算子Cφ与微分算子乘积CφD的本性范数给出估计.

令a∈，定义.

定理4 固定α>0，且假设β≥1.设φ∈S()，假设DCφ：Fα→Bβ有界，则其中

(22)

由于CφD：Fα→Bβ有界，故有

接下来证明

(23)

设{zj}j∈为中一序列，当j→∞时，使得|φ(zj)|→1.

由引理知，mj属于空间Fα，且在的紧子集上一致收敛到0.此外，有则对任意紧算子K：Fα→Bβ，有

由本性范数定义，有

现在证明

(24)

类似于定理3的证明，同样对r∈[0，1)，定义Kr：H()→H() ，(Krf)(z)=fr(z)=f(rz)，f∈H().

对紧算子Kr，设{rj}⊂(0，1)为一序列，且当j→∞时，有rj→1，对正整数j，算子DCφKrj：Fα→Bβ紧.由本性范数定义，有

(25)

为了证明式(24)，仅需证明

(26)

和

(27)

(28)

很显然，有：

(29)

现在，考虑

(30)

其中N∈足够大，使得对所有j≥N，有且：

由于CφD：Fα→Bβ有界，由文献[4]中的定理3，有φ=CφD(z2/2)∈Bβ，且

(31)

当j→∞时，在的紧子集上有rj2frj″一致收敛到f″，则有

(32)

对上式取极限N→∞，得

因此，

P2GC

(33)

由式(28)～式(30)及式(32)、式(33)，可得

(34)

4 DCφ：Fα→Bβ的新刻画

本节给出了算子DCφ：Fα→Bβ的有界性、紧性和本性范数的一个新刻画.在证明相关定理之前，先给出一些定义以及后续定理证明中将要用到的一些引理.

设v：→R+是一个连续、严格正且有界的函数，加权空间为所有满足∞的解析函数(f∈H())组成.在范数下为一Banach空间.若对所有的z∈，有v(z)=v(|z|)，此时权v称为径向的.v的关联权重定义如下：[7]

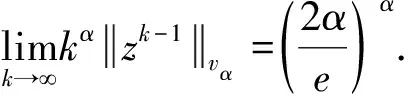
引理6[8]设v和w是径向的，是在的边界处趋于零的非递增权重，则下列陈述成立：

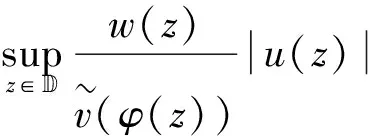
引理7[7]设v和w是径向的，是在的边界处趋于零的非递增权重，则下列陈述成立：

定理5 设α为一正整数，β≥2，且φ∈S()，则算子DCφ：Fα→Bβ有界当且仅当

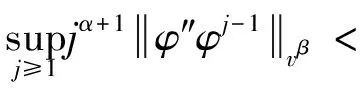
(35)

证明：由文献[4]，算子DCφ：Fα→Bβ有界当且仅当

(36)

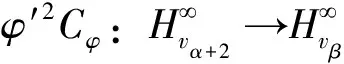
由引理5，有DCφ：Fα→Bβ有界当且仅当

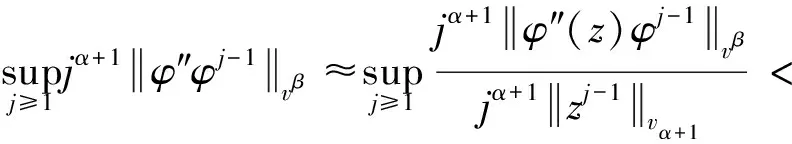
定理5证明完成.

定理6 设α为一正整数，β≥2，且φ∈S()，假设算子DCφ：Fα→Bβ有界，则其中

本性范数的上限估计由(DCφf)′(z)=f″(φ(z))(φ′(z))2+f′(φ(z))φ″(z).很容易有

对于本性范数的下限估计.由定理3、引理5以及引理6，有

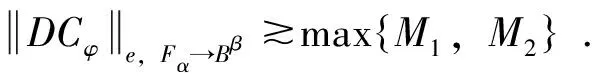
定理7 设α为一正整数，β≥2，且φ∈S()，假设算子DCφ：Fα→Bβ有界，则算子DCφ：Fα→Bβ紧当且仅当和

5 CφD：Fα→Bβ的新刻画

定理8 设α为一正整数，β≥1，且φ∈S()，则算子CφD：Fα→Bβ有界当且仅当

(37)

证明：由文献[4]，算子CφD：Fα→Bβ有界当且仅当

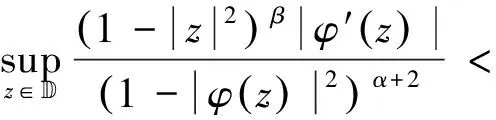
(38)

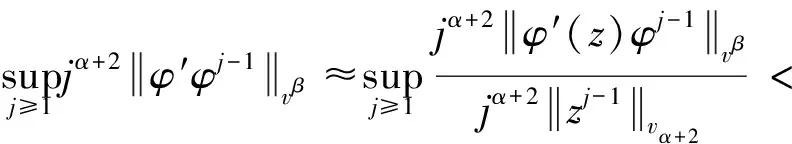
定理8证明完成.

定理9 设α为一正整数，β≥1，且φ∈S()，假设算子CφD：Fα→Bβ有界，则

本性范数的上限估计由(CφDf)′(z)=f″(φ(z))φ′(z)确定.很容易有

对于本性范数的下限估计，同样，由定理4、引理5以及引理6，有

定理10 设α为一正整数，β≥1，且φ∈S().假设算子CφD：Fα→Bβ有界，则算子CφD：Fα→Bβ紧当且仅当

致谢：衷心感谢导师胡俊云教授的悉心指导.