一种基于维数缩减的单变元Coppersmith 算法*

赵春智，曹金政，程庆丰

信息工程大学网络空间安全学院，郑州450001

1 引言

1977 年，麻省理工学院的三名学者Rivest、Shamir 和Adleman[1]提出了著名的RSA 方案.RSA是世界上第一个完整的公钥加密(public key encryption，PKE) 方案，它不仅可以用于加密，还可以用于数字签名，并且简单易实现.如今RSA 公钥加密方案被广泛应用于信息行业.1982 年，Lenstra 等人[2]提出了求解最短向量问题(shortest vector problem，SVP) 的LLL 算法.该算法是高斯算法在高维上的拓展，实际上是一个附加条件的整系数Gram-Schmidt 正交化过程，并且可以在多项式时间内得到一个较短的格向量.利用格的相关理论攻击RSA 的思路起源于Coppersmith[3]在1996 年发表的一篇论文，该论文针对RSA 部分明文泄露的情况将恢复全部明文等价于求解一个单变元模方程，然后构造相应的格并通过LLL 算法求解格中较短向量来将该模方程转化为整数环上的方程，最后利用整数环上求解多项式方程的一般方法进行高效求解.这篇论文的发表引发了国际密码学界研究利用格基约化技术攻击公钥密码系统的浪潮.随后，Coppersmith[4]于1997 年对利用LLL 算法求解模多项式方程小根的方法进行了总结和完善.1999 年，Coupé[5]等人通过对针对低指数RSA 的Coppersmith 算法进行大量实验，发现实验中未知量上界接近于理论上界，进一步验证了Coppersmith 算法的实用性.同时他们证实了当模数的大小超过未知量大小的e倍时，明文能够通过Coppersmith 算法被有效恢复.2000 年，Boneh 和Durfee[6]在Coppersmith 算法的基础上改善了Wiener 的低解密指数攻击的效果，他们将解密指数d的上界提高到N0.292，即当d ＜N0.292时，攻击者可以在多项式时间内获得私钥d.2003 年，Blömer 和May[7]基于Coppersmith 算法提出了一种新的算法，他们表明对于已知的最高有效位，公钥[N0.5，N0.725] 时，或对于已知的最低有效位，公钥e ＜N7/8时，RSA 系统就能被攻破.2006 年，Jochemsz 和May[8]针对一般的多变元模多项式方程和多变元整系数多项式方程，给出了“基础策略”(basic strategy)和“拓展策略”(extended strategy)，进一步完善了Coppersmith 算法中格的构造方法.2009 年，Coron 等人[9]利用寻找多变元模方程小根的Coppersmith 算法将RSA 的故障攻击扩展到一大类已知部分消息的情况.他们成功地攻击了ISO/IEC9796-2 编码标准的几个随机版本，验证了新方法的有效性.实验表明，如果已知一个包含160 位未知消息摘要的错误签名，此方法能在很短的时间内分解一个2048 位模数.2010 年，Cohn 和Heninger[10]提出了一种用于多项式时间内寻找模代数数域上理想的多项式方程小解的Coppersmith 算法，并给出了类似于原Coppersmith 算法的平行证明.2013 年，Coron 等人[11]通过对原始Coppersmith算法中格矩阵进行整系数线性变换，减小了格矩阵的系数，同时将算法的渐进复杂度由O(log8+ϵN) 降为O(log6+ϵN).此外，他们设计了一种可以加速穷举的方法，使得未知量的实验上界有效接近于理论上界.同年，Aono[12]提出了一种针对模方程组的Coppersmith 算法，该算法中的格是由求解单个模方程的格组成的.他们证实，在模数N固定、私钥d ＜N(9l-5)/(12l+4)的情况下，已知l对公钥就可以分解模数N.2014 年，Bi 等人[13]提出了Coppersmith 算法的两个加速技巧，首先他们通过对格矩阵的系数进行舍入来减少算法的运算时间，其次他们使用链接的技巧加速了在穷举未知量高位比特情况下Coppersmith算法的效率，同时他们对Coppersmith 算法的小根上界进行了推广证明.2016 年，Chinburg 等人[14]将Coppersmith 寻找多项式小根的方法同模整数和代数曲线的adelic 子集的容量理论建立了新的联系，并利用相应的容量理论证明了求解单变元方程的Coppersmith 算法中界的最优性.在2017 年CCS 上，Nemec 等人[15]利用RSALib 库中参数的特征以及求解单变元线性方程的Coppersmith 算法提出了一种新的启发式整数分解算法，由于RSALib 库应用广泛，该攻击的实用性很强.2019 年，孙哲蕾等人[16]利用Coppersmith 算法改进了Bunder 等人的分析结果，扩大了可以实现的三种变型RSA 方案小解密指数攻击的参数范围.此外，他们通过设置额外的参数尽可能优化格的结构，提高了算法的可用性.2021年，王云飞等人[17]提出了一种基于行公因子提取的Coppersmith 算法，他们首先用预处理算法降低矩阵系数，然后对矩阵进行分块提取公因子再使用LLL 算法约化的处理，提高了Coppersmith 算法的运行效率，在实验中效率最高可提升22.64%.同年，Nitaj 等人[18]利用Coppersmith 算法攻击了基于三次Pell方程的RSA 密码系统的变体，其中公钥(N，e) 和私钥(N，d) 满足ed ≡mod(p2+p+1)(q2+q+1).与此同时，Moussaid 等人[19]提出了一种新的Coppersmith 算法的实现方式，主要是通过实验找到大小合适的格来提高运行效率.2022 年，May 等人[20]利用Coppersmith 算法提出了一种新的CRT 指数泄露攻击，该攻击分为两个步骤: 首先利用Coppersmith 算法求解系数k和l，然后利用k和l以及多变元Coppersmith 算法分解模数N.同时，他们通过实验验证了新方法在e ≈N1/12时有效.同年，Shi 等人[21]对RSA 的B型变体进行了进一步的密码分析，他们表明，对于针对RSA 的几种常见的攻击，RSA的B型变体不如标准RSA 安全性高.

格是n维空间Rn的离散子群，格的一组格基是由Rn中n个线性无关的向量构成的.格基约化就是将格中给定的一组格基向量进行一系列整数线性变换，得到一组新的基向量，使其模长较短或两两几乎正交.目前格的研究涉及代数、几何等许多数学领域，格在物理学、信息安全、密码学等领域中有着非常重要的应用.Coppersmith 算法的核心是解决格中一类经典困难问题—最短向量问题，该问题的解决依赖于格基约化算法性能的优劣.现阶段Coppersmith 算法应用的格基约化算法为LLL 算法，该算法可以在多项式时间内求得格中近似最短向量.理论上，格基约化算法约化效果越好，Coppersmith 算法的运行效率越高.但事实上，由于Coppersmith 算法中的格矩阵系数很大，一些需要枚举的格基约化算法并不适用于Coppersmith 算法.

原有的基于小根问题的单变元Coppersmith 算法构造的格矩阵维数偏大，这就导致原算法存在求解效率低等问题.实验表明，在实际求解过程中，较小维数的格矩阵也能成功求解方程.本文研究了基于小根问题的单变元Coppersmith 算法，并在原算法的基础上做了一些改进，主要是通过一些技术手段降低了原有Coppersmith 算法中构造的格矩阵的维数，同时还能在实际求解过程中以较大概率求解方程.具体改进有以下三点:

(1) 采用缩减格矩阵维数的启发式算法.根据Nguyen 等人的工作成果，令格矩阵从一个较小维数开始并依次增加e维来进行约化，直至成功求解方程.

(2) 利用概率统计的方法对起始维数进行优化.由于Coppersmith 格不是随机格，改进1 可以进一步加强针对性.本文通过概率统计的方法获得了关于LLL 算法在Coppersmith 格上的约化效果的新估计，依据此估计，本文对格矩阵约化的起始维数进行了优化.

(3) 利用已知的未知明文比特位数对原来的未知量进行变量代换，使得新未知量的比特数较小，求解复杂度减少约2 比特.

2 预备知识

本节将介绍格、最短向量问题、Gram-Schmidt 正交化的基本定义，同时也会给出LLL 算法的伪代码及相关性质.本节内容主要来自于文献[13] 与文献[22].

2.1 格的基础知识

定义1(格) 设给出一组线性无关的向量b1，b2，···，bn Rm，则由b1，b2，···，bn的整系数线性组合构成的集合称为格L，即L{z1b1+z2b2+···+znbn|z1，z2，···，zn Z}.称b1，b2，···，bn是格L的基，其中n为格的秩，m为格的维数(n ≤m).

定义2(最短向量问题) 求解格L中模长最短的非零向量v，其中v满足‖v‖ ≤‖vi‖，对任意的vi L{0}.

定义3(Gram-Schmidt 正交化) 给定一组格基v1，v2，···，vn，令

其中μi，j＜vi，＞/，i2，3，···，n，则，···，正交，该过程被称为Gram-Schmidt 正交化.

2.2 LLL 算法

一个格有无数组格基，而格基约化算法就是将格中给定的一组格基进行一系列整数线性变换，使得到的新格基满足格基向量模长较短或两两几乎正交.Lenstra 等人[2]在1982 年提出LLL 算法来分解有理数域上的非零多项式，作为最著名的格基约化算法之一，该算法可以在多项式时间内求得格中近似最短向量，见算法1.LLL 算法在求解整数线性规划、在整数上分解多项式以及现代密码分析中起着重要作用.

LLL 算法输出的约减基有如下性质.

引理1设v1，v2，···，vn是LLL 算法输出的约减基，则v1，v2，···，vn满足

关于LLL 算法的约化效果，有以下定理.

定理1设L为维数为n的格，δ是LLL 算法的参数，β1/(δ-1/4)，则LLL 算法输出的首向量v1满足:

证明:对于1＜i ≤n，由引理1 可得

根据Nguyen 等人[23]的工作，有如下假设:

假设1设δ接近1.给定一个维数n足够大(n ＞40) 的随机格L作为输入，则参数为δ的LLL 算法输出的第一个基向量v1满足

2.3 小根问题和单变元Coppersmith 算法

在1996 年的欧密会上，Coppersmith 描述了如何使用格基约化技术来寻找多项式方程的小根，即求解“小根问题”.基于部分明文泄露的“小根问题” 是指: 对于RSA 系统，已知一部分明文消息m0，即密文c(m0+x)e(modN)，现尝试恢复出未知的部分明文x.这里明文泄露指已知明文m的若干连续高比特位.此时，我们有

其中mH和mL分别是已知高比特位和未知低比特位的十进制表示，i是未知低比特位数.由于明文比特位数M ≤，不妨设M，此时我们有iM-l(l是已知高比特位数).由此，可以得到模方程

1996 年，Coppersmith[3]提出了利用LLL 算法求解模多项式方程小根的方法.该方法将未知明文作为求解模方程的未知量，然后利用LLL 算法对格基进行约化，找到模长足够短的格向量，最后求解出未知明文.一般来说直接求解模方程是比较困难的，但求解整数环Z上的方程是较为容易的，常见的方法有Gröbner 基[24]等.Coppersmith 通过利用LLL 格基约化算法和Howgrave-Graham 定理，成功地将模方程转化为整数环Z上的方程，极大简化了求解难度.下面是Howgrave-Graham 定理.

定理2设g(x) 是一个n次单变元多项式.此外，令t为正整数.假设g(x0)0 (modNt)，其中

那么g(x0)0.

下面给出基于小根问题的单变元Coppersmith 算法(算法2).

3 改进Coppersmith 算法

原始Coppersmith 算法中格矩阵是根据LLL 算法约化效果达到定理1 中上界构造的.大多数情况下，LLL 算法的实际约化效果要比理论上界好得多，所以实际情况下求解问题所需的格矩阵维数要比估计的小得多.格矩阵的维数越大，LLL 算法运行时间越长.因此原Coppersmith 算法求解效率较低，尤其是在未知比特数较大时，LLL 算法运行效率极低.为优化上述问题，本文从以下方面对Coppersmith 算法进行改进:

· 采用缩减格矩阵维数的启发式算法.根据Nguyen 等人的工作成果，令格矩阵从一个较小维数开始并依次增加e维来进行约化，直至成功求解方程.

· 利用概率统计的方法对起始维数进行优化.由于Coppersmith 格不是随机格，将LLL 算法对随机格的约化效果直接应用到Coppersmith 格会导致一定的误差.因此，本文通过概率统计的方法获得了关于LLL 算法在Coppersmith 格上的约化效果的估计.利用此估计，本文对格矩阵开始约化的维数进行了优化，提高了改进算法的成功率.

· 采用变量代换的技巧.利用已知的高比特位信息对原来的未知量进行替换，使得新未知量的比特数下降，进而降低求解复杂度.

下面将详细介绍这三点改进.

3.1 维数缩减

实际情况中，LLL 算法的约化效果往往要比定理1 中所给的上界好得多.本节尝试从可能的较低维数开始，之后依次增加e维对矩阵进行约化，直至成功求解方程.实验表明这个启发式算法在大多数情况下是有效的.根据Nguyen 等人[23]的工作，对于随机格，我们可以获得LLL 算法约化效果的较为精确的估计.而Coppersmith 方法中使用的格基和文献[23] 中选取的Ajtai 类型的格基具有一定的相似性，因此我们认为可以用假设1 来大致描述随机选取的Coppersmith 格的约化效果.本节就是从假设1 着手，获得一个平均意义上的可能成功求解方程所需的较低维数，并以此维数为起点，逐次增加e维进行约化，直至成功求解方程.

根据(4)式，两个Coppersmith 格的维数差约为

可以验证，当e3、β4/3、n ＞115 时，维数差n1-n ＞3.

在实际求解中，可令格矩阵维数从n1-「(h1-h)开始，依次增加e约化求解，直至成功求解方程.实际上，由于上界X略大于未知量，实际求解所需的矩阵维数可能比n1-「(h1-h)还要小.因此，当矩阵维数为n1-「(h1-h)时，方程有较大概率能够得到解.

3.2 维数优化

由于随机选取的Coppersmith 格严格意义上来说不是随机格，将Nguyen 等人的工作[23]直接应用到Coppersmith 格会导致一定的误差.因此，本节通过引入概率统计的方法获得了以高概率成立的LLL算法在Coppersmith 格上约化效果的新估计，并由此提出新的未知量上界，优化了起始维数.值得一提的是，对于随机格，Nguyen 等人[23]认为μi+1，i’s 是独立同分布的，进一步我们通过大量实验统计了平均意义下Coppersmith 格的μi+1，i’s 的分布情况以及μi+1，i和μj+1，j(1≤j ＜i ≤n-1) 的相关系数(见图1).我们发现除了首尾个别μi+1，i’s 外，其他μi+1，i’s 几乎同分布.对于首尾的μi+1，i’s，通过观察可知其取值都偏小，对我们的估计没有负面影响.此外，我们发现μi+1，i和μj+1，j(1≤j ＜i ≤n-1) 的相关系数几乎都处于区间[-0.05，0.05] 内，所以我们认为μi+1，i’s 两两相互独立.下面给出假设2.

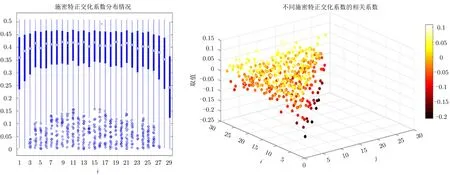
图1 μi+1，i 的分布情况以及μi+1，i 和μj+1，j 的相关系数Figure 1 Distribution of μi+1，i and correlation coefficients of μi+1，i and μj+1，j

假设2将Coppersmith 格的Gram-Schmidt 正交化系数μi+1，i(1≤i ≤n-1) 视为随机变量，则μi+1，i’s 独立同分布.

根据假设2，随机变量Yi+1，i:1/(δ-) 也独立同分布.同时根据(1)式，我们有

当i-j很大时，ηi，j近似服从标准正态分布.通过上面的推导，我们有

3.3 变量代换

本文利用了变量替换技巧，有效降低了算法求解的复杂度.首先已知部分明文信息m0，其次明文m的比特数也是已知的，此时就可以利用这些信息来降低算法的求解复杂度.鉴于m0和m的比特数l和M都已知，未知明文信息x的比特数k是很容易得到:kM-l.现令

综合以上几点，给出改进后的基于小根问题的Coppersmith 算法(算法3).

4 性能分析

本文使用SageMath 9.2 实现Coppersmith 算法以及相关改进算法.测试计算机使用1.80 GHz Intel Core i7 处理器和8 GB 内存，操作系统为win 10.实验中模数N均为1024 比特数，公钥e3，LLL参数设置为δ0.99.本文随机选取5 组1024 比特模数N，并对322、325、327、329、332 未知比特数分别进行10 次实验，并记录相应的Gram-Schmidt 正交化系数μi+1，i’s 的频数分布情况.对于每组数据{a1，a2，···，am}，我们发现a，σ分别稳定于1.2 和0.1.在进行改进2 时，对于322、325、327、329、332 五组未知比特数，我们分别取z2.57，2.75，2.85，2.96，3.11，t30，对应概率分别为0.955，0.956，0.955，0.956，0.955.图2 是t30 时U(t+1)1的频率分布图，图中的曲线是均值为1.2、标准差为0.018正态分布曲线.从图中可以了解到U(t+1)1是近似服从参数为(a，σ/) 的正态分布的.可以预测，当t的值更大时，U(t+1)1的分布和参数为(a，σ/) 的正态分布更加契合，这反映了我们改进2 的有效性.

图2 U(31)1 的频数分布直方图Figure 2 Frequency of U(31)1

首先通过比较几种算法在未知比特数分别为322、325、327、329、332 的情况下的所消耗的时间，我们发现I-Coppersmith 算法较Coppersmith 算法效率有较大提升.总的来说，I-Coppersmith 算法运行时间较Coppersmith 算法减少约50%.理论上讲，未知比特数越大，改进效果越好，效率提升越明显.具体结果如表1 所示(单位: s).在成功求解方程的条件下，各算法的所需格维数如表2 所示.由于改进1 和改进2 是启发性的，本文还考虑了实验中两种算法在起始维数d成功的概率，结果如表3 所示.由表2—3 可知虽然改进2 较改进1 降低的维数少，但其成功率较改进1 有大幅提升.

表1 4 种算法运行用时比较Table 1 Running times of four algorithms

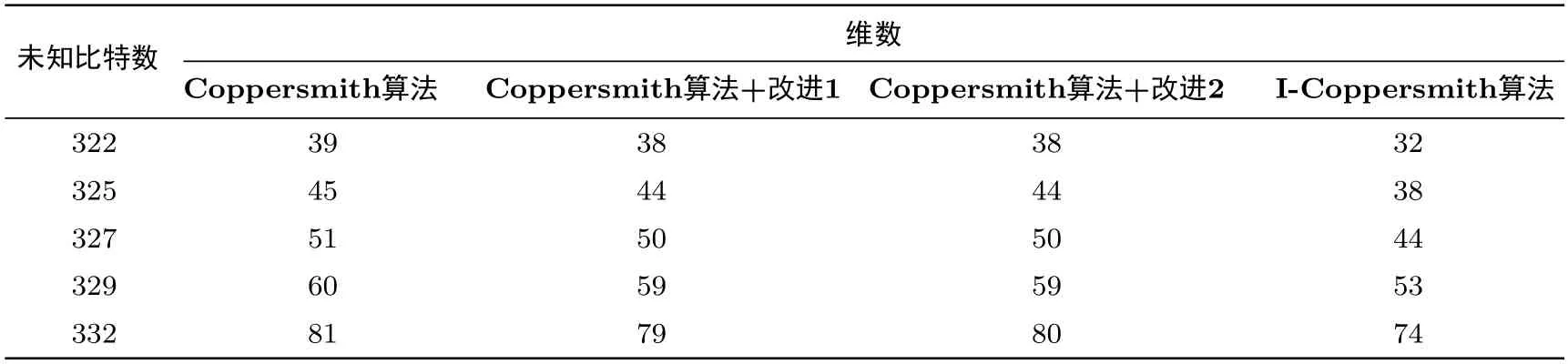
表2 4 种算法的格维数比较Table 2 Lattice dimensions of four algorithms

表3 两种算法成功率比较Table 3 Probabilities of two algorithms

本文利用概率统计的方法优化了定理1 中的LLL 约减基首向量模长的上界，之后比较了优化后LLL约化上界和原始上界的大小.在不同未知比特数下，新约化上界与原始约化上界的比值如表4 所示.

表4 新上界与原始上界在不同维数下的比值Table 4 Ratios of new upper bound to original upper bound in different dimensions

由表4 可知，随着格维数增大，LLL 算法的新约化上界与原始约化上界的比值呈现减小的趋势，这说明在较大未知比特数的情况下，新上界的改进效果更加明显.根据新的约化上界，本文提出了新的变量上界X2.在格维数相同的情况下，X2-X1与X1的比值如表5 所示.

表5 X2 -X1 与X1 的比值Table 5 Ratios of X2 -X1 and X1

由表5 可知，在格维数相同的情况下，未知量上界X2要比上界X1高出1.7%—3.2%.这就意味着采用上界X2的Coppersmith 算法能够求解更大的未知量.虽然未知量上界越大，Coppersmith 算法运行效率越低，但鉴于Coppersmith 算法的效率主要与矩阵维数有关，未知量上界大小对求解效率的影响可以忽略不计.

5 总结

本文围绕小根问题，分析了针对小根问题的单变元Coppersmith 算法，在原Coppersmith 算法的基础上提出了I-Coppersmith 算法.通过在多个不同未知比特数情况下进行实验，比较消耗时间、格矩阵维数等指标，得到的结论为新算法求解效率较原算法有较大提高.总体来说，新算法使用了维数缩减和变量代换的技巧，两者都降低了需约化的格矩阵维数，使得求解效率较原算法有一定的提升，算法的实用性得到了提高.后续工作中将对算法从3 个方面进行完善和优化: (1) 进一步优化实验参数;(2) 理论上进一步说明削减维数后算法仍然成功的鲁棒性;(3) 将概率统计分析的方法应用到更大模数的RSA 系统中.