适用于云存储的可更新签密算法*

原毓婧，刘振华，2，王保仓

1.西安电子科技大学 数学与统计学院，西安710071

2.密码科学技术全国重点实验室，北京100878

3.西安电子科技大学 通信工程学院，西安710071

1 引言

随着云计算技术的广泛应用，人们更倾向于将数据外包存储到云数据存储中心，以此达到减少本地服务器的存储压力、便于后续各类计算等目的.然而，云存储在为人们带来便利的同时，也带来了数据安全问题.为了确保外包数据的机密性，需要考虑数据本身的安全性，常用的解决办法是将数据进行加密后再上传到云数据存储中心.但在实际应用中，经常存在掌握云端数据密钥的用户离开系统、密钥泄露不可避免导致数据泄露等情况，这些都需要对加密系统设计有效的机制来保证系统的安全，特别是密钥的安全.

在这种情况下，可更新加密算法(updatable encryption，UE) 应运而生，它支持定期更改或轮换用于保护数据的加密密钥，以降低密钥随着时间推移而泄露的风险和影响.在可更新加密算法中，由一个(或两个) 用户密钥加密生成的密文存储在服务器端，随后服务器可以通过使用客户端提供的更新令牌将密文从旧密钥更新到新密钥下，并且该过程不需要解密密文，这样重加密所有密文的操作可以外包给云服务提供商.可更新加密算法由Boneh 等人[1]在CRYPTO 2013 会议上正式提出，其从代理重加密中获得灵感，使用密钥同态伪随机函数构造了一个对称可更新加密算法.

然而，Boneh 等人提出的算法仅仅解决了相对较弱的保密目标，没有考虑到数据的完整性.实际上可更新加密本身并不能完全保证数据的完整性，当数据外包给不完全可信的云服务提供商时，它可能会随意篡改或插入密文.为解决上述问题，Everspaugh 等人[2]提出了一个可更新的认证加密算法，实现了完整性和更高的机密性，但他们的工作仅适用于较小或非常有价值的数据，当明文数据较大时，该算法会造成巨大的开销，这是因为可更新加密有两种不同的形式.根据更新令牌是由特定密文生成的还是与密文无关的，将可更新加密分为两种类型，前者称为密文相关(ciphertext-dependent) 的可更新加密[3]，后者称为密文独立(ciphertext-independent) 的可更新加密，密文相关的算法允许细粒度地控制哪些密文应该针对新的密钥重新加密[4]，但远没有密文独立的算法高效和方便.在密文独立的算法中，更新令牌只依赖于新密钥和旧密钥，并允许使用一个令牌对所有密文重新加密，与密文相关的令牌相比，这样一个令牌的腐败可能赋予敌手更强的能力，Everspaugh 等人[2]提出的正是一种密文相关的可更新加密算法.当需要对大量密文进行密钥轮换时，密文独立算法在效率和易用性方面明显优于密文相关算法，因此Lehmann 等人[5]在2018 年提出了一个基于ElGamal 的密文独立可更新加密算法RISE，该算法使用一个令牌更新所有密文，可以清晰体现选择攻击下的后向和前向安全，但该算法没有考虑完整性，且仍然只考虑了对称密码体制.

为满足不同的需求，需要考虑非对称密码体制的更新功能.2021 年，Cini 等人[6]引入了可更新签名(updatable signature，US) 的概念，讨论了几种可作为其他密码算法构建模块的密码原语，提出了几种不同的可更新签名算法，取得了在选择消息攻击下具有存在不可伪造性和更新不可链接性.另外，2015 年郑玉良等人[7]首次提出了签密的概念.签密技术不仅可以在一个逻辑步骤内完成签名和加密两项功能，同时有效地实现保密性和认证性，而且在计算量和通信成本方面都优于传统的“先签名后加密” 算法.

在诸如云邮箱(cloudmail) 等场景中，接收方由于各种原因未能及时查看或下载邮箱中的文件，而存储在云服务提供商处的文件中可能包含隐私或敏感信息，因此云服务提供商需要定期对存储在邮箱中的文件进行更新，同时，接收方在之后下载时需要确保文件的机密性和完整性，并且确认该邮件正是发送方发出的.Everspaugh 等人提出的可更新认证加密算法[2]仅在对称场景下实现了完整性和机密性，而具有可更新功能的签密算法可以在非对称场景下同时达到完整性和机密性，并且能够对大量密文进行密钥轮换，满足上述需求，但据我们所知目前没有对可更新签密算法的研究.基于此，本文将研究云存储环境[8]下非对称场景中用户数据的完整性和机密性相关的问题，设计一个基于ElGamal 加密和BLS 签名的可更新签密算法，并建立可更新签密的系统模型、形式化定义和安全模型，最后运用归约等方法证明可更新签密算法(updatable sign(en)cryption，USE) 具有密文不可区分性、更新不可链接性和数据完整性.

2 预备知识

2.1 双线性映射

假设G、GT是阶为素数p的循环群，g为G的生成元，则称ˆe:G×G →GT为一个映射.如果它满足下列条件，则称为双线性映射:

(1) 双线性: 对于任意g，，a，，有(ga，hb)(g，h)ab;

(2) 非退化性: 存在生成元，使得(g，g)/1;

(3) 可计算性: 对于任意g，，a，，都存在一种概率多项式时间(PPT) 算法可以计算(ga，hb)，并且群G上的运算是高效的.

2.2 CDH 问题

p是一个λ比特的素数，G表示一个p阶的循环群G〈g〉，g为群G的一个生成元.计算Diffie-Hellman 问题(computational Diffie-Hellman problem，CDH 问题) 定义如下:

给敌手A一个元组(G，p，g，ga，gb)，其中a，是随机选择的，CDH 问题为计算gab G.CDH假设定义为，对任何概率多项式时间(PPT) 敌手A，其解决CDH 问题的概率是可忽略的，即

2.3 DDH 问题

p是一个λ比特的素数，G表示一个p阶的循环群G〈g〉，g为群G的一个生成元.判定Diffie-Hellman 问题(decisional Diffie-Hellman problem，DDH 问题) 定义如下:

给敌手A两个元组(G，p，g，ga，gb，gab) 和(G，p，g，ga，gb，gc)，其中a，b，是随机选择的，DDH问题为从这两个元组中判定哪个是gab.DDH 假设定义为，对任何概率多项式时间(PPT) 敌手A，其解决DDH 问题的概率是可忽略的，即

3 可更新的签密算法

3.1 算法框架

3.1.1 系统模型

一个可更新的签密算法主要由以下3 个参与方组成，其系统模型如图1 所示:

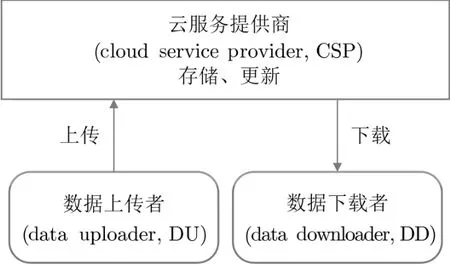
图1 系统模型Figure 1 System model

(1) 数据上传者(data uploader，DU): 数据上传者是想要分享自己数据的实体，他/她可以根据接收者的公钥和自身的私钥签密数据后上传至云端.

(2) 数据下载者(data downloader，DD): 数据下载者是数据上传者想要分享数据的对象，他/她不仅可以访问数据上传者存储在云服务提供商处的数据，而且还可以成功下载、验证和解密密文.

(3) 云服务提供商(cloud service provider，CSP): 云服务提供商拥有对云数据的管理权限，主要负责数据的存储和更新.云服务提供商不一定是完全可信的，即它会执行每个请求，但试图从过程和结果中获得尽可能多的信息，甚至随意篡改或插入密文.

3.1.2 形式化定义

一个可更新的签密算法的形式化定义如下，主要包含5 个概率多项式时间算法(用S代表发方，R代表收方):

· 密钥生成(KeyGen): 输入参数λ，数据上传者DU 和数据下载者DD 分别运行该算法生成初始时期密钥kS，0(skS，0，pkS，0) 和kR，0(skR，0，pkR，0);

· 令牌生成(Next): 输入kS，e，DU 运行该算法生成更新令牌ΔS，e+1;输入kR，e，DD 运行该算法生成更新令牌ΔR，e+1;

· 数据签密(SignCrypt): 输入消息m，skS，e和pkR，e，DU 运行该算法生成签密文Ce;

· 数据解签密(Unsigncrypt): 输入签密文Ce，pkS，e和skR，e，DD 运行该算法，输出消息m或⊥;

· 签密文更新(Upd): 输入签密文Ce以及更新令牌ΔS，e+1，ΔR，e+1，云服务提供商CSP 运行该算法输出更新后的签密文Ce+1.

3.1.3 安全模型

Lehmann 等人[5]考虑到可更新加密算法通过两种方式产生密文，一种是直接加密，另一种是对之前的密文进行更新，他们要求上述两种方法都必须具有以下安全性质:

(1) 令牌安全: 更新密文的特性不应降低加密算法的标准IND-CPA 安全性，即更新的密文泄露甚至所有令牌的暴露都不会增加敌手破坏加密算法的优势[9].

(2) 前向安全: 在某个时期e*腐败密钥的敌手在解密他在该腐败之前在时期e ＜e*中获得的密文方面没有任何优势[10].

(3) 后向安全: 在某个时期e*腐败密钥的敌手在解密他在该腐败之后在时期e ＞e*中获得的密文方面没有任何优势[11].

(4) 选择安全: 一个敌手可以自适应地腐败当前和所有之前的密钥及令牌.

本文基于郑玉良等人[7]的理论，延续并改进之前Lehmann 等人[5]和Cini 等人[6]的工作，在存在临时密钥和令牌腐败的情况下保证密文机密性和数据完整性，包括上述令牌安全、选择安全以及前向和后向安全性.设表示挑战时期，eend表示游戏的最后时期.

定义1 集合L，，C，K，T，S，Q用于跟踪生成和更新的签密文与签名，以及敌手A腐败密钥或令牌、学习挑战签密文的时期，其定义如下:

·L: 通过调用签密谕言机OSigncrypt或更新谕言机OUpd生成的非挑战签密文(Ce，e) 集合;更新谕言机OUpd仅更新L中包含的签密文.

·C: 敌手A学习挑战签密文新版本的所有时期e的集合.

·K: 敌手A腐败密钥ke的所有时期e的集合.

·T: 敌手A腐败更新令牌Δe的所有时期e的集合.

·S: 敌手A在时期e查询签名谕言机Oσ或在时期e-1 查询更新谕言机OUpd(σ)得到的所有(e，m，σe) 的集合.

·Q: 敌手A通过签密谕言机OSigncrypt，更新谕言机OUpd或解签密谕言机OUnsigncrypt获得的诚实明文的集合.

定义2在和挑战者交互期间，敌手可能会拥有对一些谕言机的访问权，其定义如下[5]:

(1)OSigncrypt(m，e): 输入一个消息和时期e，计算θe ←Enc(pkR，e，m) 和σe ←Sig(skS，e，θe)，输出签密文Ce(θe，σe)，添加Ce到密文列表L ←L ∪{(Ce，e)}中并返回签密文Ce给敌手.

(3)OUpd(Ce-1): 输入一个签密文Ce-1，检查它是否是前一个时期诚实生成的，然后计算Ce ←Upd(Δe，Ce-1)，并将(Ce，e) 添加到L，最后输出Ce给敌手.

(4)OCorrupt({token，key}，e*): 该谕言机分别模拟CSP 和DU 的自适应腐败，敌手可以请求当前或

任何以前时期的密钥或更新令牌.

— 在输入token 时，e*≤e，谕言机返回Δe*，即更新令牌被泄露.在这种模式下调用谕言机使T ←T ∪{e*}.

— 在输入key 时，e*≤e，谕言机返回ke*，即密钥被泄露.在这种模式下调用谕言机使K ←K ∪{e*}.

(6)OUnsigncrypt(Ce): 输入一个签密文Ce，返回m ←Unsigncrypt(ke，Ce) 或错误符号⊥.

(7)Oσ(m): 输入一个密文，计算σe，添加σe到签名列表S ←S ∪{(e，m，σe)}中并返回签名给敌手.

(8)OUpdσ(σe-1): 输入时期e-1 的签名σe-1，计算←Σ.Adapt，返回σe给敌手.

定义3(泄露集合) 密文独立的可更新加密算法的主要优势在于可以使用单个令牌将所有密文从一个时期更新到下一个时期.然而，在敌手腐败许多密钥、令牌和更新后的挑战签密文后，令牌的通用性也带来了许多问题.实际的算法使敌手能够获得更多的信息，比如一个令牌可能不仅允许更新密文，还允许将密文“退化” 到前一时期，即更新是双向的，甚至允许仅通过一个令牌来更新和退化密钥.

一般通过定义扩展集K*，T*，C*来捕获不能通过谕言机直接捕获的密钥、令牌的“泄露”，即捕获敌手从直接获得的令牌、密文或密钥中推断出的信息[12].

在许多算法中，更新令牌不仅允许更新密文，还允许更新密钥本身，换言之，如果敌手已经获得了e时期的密钥ke和更新令牌Δe+1，那么也能得到新的密钥ke+1.如果这是唯一可能得到的密钥，称之为单向密钥更新;如果额外还有可能的密钥退化，即密钥ke可以从ke+1和Δe+1中获得，称之为双向密钥更新.

单向密钥更新: 若()∨(Corrupt-key(e-1))，则

双向密钥更新: 若()∨(Corrupt-key(e-1))∨(Corrupt-key(e+1)∧e+1)，则

敌手可以从两个随后的密钥ke和ke+1中准确地推导出一个更新令牌Δe+1，那么定义一个扩展集T*，它包含敌手直接获得的或从腐败的密钥中派生出来的所有更新令牌.

为了捕获敌手知道挑战签密文的所有时期，接下来定义包含所有挑战等价时期的集合C*，挑战等价时期是敌手知道挑战签密文当前版本的每个时期.这可以通过直接调用挑战签密文谕言机或者由敌手通过(一系列) 更新计算来获得，根据更新是单向的还是双向的来区分这两种情况.

最优泄露集合只捕获执行密文独立的更新所需的最少推论，即T*T，K*K，C*也即没有令牌推断，密钥不能通过一个令牌更新并且密文更新只是单向的.

S*通过被腐败的签名集合S，T*，K*中的信息以及递归谓词Corrupt-Sig 定义以捕获由签名更新可推导出的信息.

定义4(密文不可区分模型) 如果对所有概率多项式时间敌手A都有

关于可忽略函数ϵ成立，那么一个可更新的密码算法是具有密文不可区分性(IND-ENC) 的.

该模型遵循典型的IND-CPA 模型[13]，但额外授予敌手对谕言机ONext，OUpd，OCorrupt，OUpd～C的访问权.“挑战等价” 时期是敌手知道挑战签密文当前版本的每一个时期，为了排除平凡的胜利，A在任何挑战等价的时期都不能腐败密钥.这可以通过直接调用挑战签密文谕言机来获得，也可以由敌手自己通过(一系列) 更新来计算.敌手已知的挑战等价时期(C*) 和密钥(K*) 的确切集合取决于泄露集合，在证明安全性时必须指定这些集合，对于本文算法的安全性证明，已在定义3 中说明了泄露集合.

进一步地，密文不可区分模型并不要求更新后的密文看起来像全新的密文，特别是不要求它们跨时期不可链接.虽然密文之间的可链接性并不一定会泄露底层明文的信息，但在考虑上下文时，它可能会泄露大量信息.这样一来，它与人们期待从可更新加密获得的直观的安全保证相违背: 即在更新之后，所有之前被泄露的消息对攻击者来说是无用的.因此，本文提出了第二个模型要求更新具有不可链接性.

定义5(更新不可链接模型) 如果对所有概率多项式时间敌手A都有

关于可忽略函数ϵ成立，那么一个可更新的密码算法是具有更新不可链接性(IND-UPD) 的.

该模型中敌手提供两个签密文C0和C1，并返回其中一个为更新的而他的任务是猜测哪个密文被更新了.我们允许敌手腐败密钥并且该实验排除了敌手获得挑战等价时期密钥的平凡的胜利.此外，即便更新算法是确定的，也不允许敌手自己将两个挑战签密文中的任何一个更新到挑战时期.

由于本文使用概率的重加密算法，密文的完整性不再能得到保证: 当敌手腐败更新令牌时，它可以通过将旧的密文更新到新的时期来生成各种有效的密文.而前两个模型并没有提供任何完整性保护.因此，需要建立数据完整性(INT-PTXT) 的安全模型.

如果敌手仅靠自己就能伪造出一条“新” 消息的有效签密文，即他成功地伪造出一个签密文，该签密文可以被有效地解密为一个他以前没有查询过签密谕言机的明文，那么敌手获胜.我们必须捕获所有的明文，因为敌手可以根据他通过谕言机得到的信息，并利用他所了解的某些密钥和更新令牌，轻松地为这些明文伪造出密文.INT-PTXT 安全模型排除了从那时起腐败了密钥和所有令牌的敌手，因为这允许为所有明文加密得到有效的密文.

定义6如果对所有概率多项式时间敌手A都有可忽略的优势

那么一个可更新的签密算法是具有数据完整性(INT-PTXT) 的.

3.2 具体算法

基于可更新加密算法RISE[5]和短签名算法BLS[14]，本节设计一个新的可更新签密算法.该签密算法基于双用户场合并采用“加密再签名” (EtS) 的方法，发送方和接收方的密钥生成算法分别是签名和加密算法的密钥生成算法.

假设现在有一个数据上传者Alice、一个数据下载者Bob 和一个云服务提供商CSP，Alice 将自己已经处理好的数据上传到CSP 处存储，由于CSP 不一定完全可信，当Bob 从CSP 处下载Alice 之前存储的数据后，他不仅可以确认该数据是否是Alice 上传的，而且可以验证数据是否完整.考虑这样一个场景，一位教师发送了许多学习资料到学生的云邮箱(cloudmail)，但学生由于种种原因没能立即接收，直到过了一段时间后他的学生才接收并下载资料来学习，那么利用本文的算法，该学生不仅可以确认这些学习资料是他的老师所上传的，而且可以验证这些学习资料的完整性以保证他可以学习到正确的知识.

设(G，g，p) 是系统参数，满足关于λ的DDH 问题和CDH 问题是困难的，p是一个λ比特的素数，hash 函数H:G →G，本文的可更新签密算法(以下简记为USE) 构造如下.

3.3 安全证明

3.3.1 密文不可区分性

定理1(USE 是IND-ENC 安全的) 可更新的签密算法USE 在DDH 假设下具有密文不可区分性.

证明:本文通过归约来证明该定理，对每个攻击USE 安全性的敌手A来说，总有一个敌手B攻击DDH 假设.

首先定义一系列游戏G0，G1，···，G˙e，其中Gi表现的和直到i-1 时期的实验完全相同，而从时期i开始，挑战签密文由三个随机群元素构成.IND-ENC 游戏可以视为G˙e+1，并且没有敌手可以在G0中获得非平凡的胜利，因为整个视角独立于挑战比特.还有待证明的是，对于所有0，1，···，˙e}，Gi和Gi+1之间的区分优势可以忽略不计，我们通过归约到DDH 来表明后续游戏的不可区分性.

3.3.2 更新不可链接性

定理2(USE 是IND-UPD 安全的) 可更新的签密算法USE 在DDH 假设下具有更新不可链接性.

证明:下面通过三个游戏来证明更新不可链接性，其中在最后一个游戏归约B到DDH 假设上.

Game0:B通过运行可更新签密的正确算法模拟所有对A的谕言机.

Game1: 当回复OUpd和谕言机查询时，B改变自己的操作，他重加密捕获到的底层消息，而不是更新提供的密文，为了能够这样做，B扩展了列表L来存储包括消息m的元组(Ce，m，e)，无论何时一个加密查询被生成.

当收到一个查询OUpd(Ce′) 时，B在L中查找相关m，返回USE.Signcrypt(skS，e′，pkR，e′，m).类似地，对于的查询，返回挑战签密文的更新版本，B在当前时期密钥下简单加密md.由于USE 中的签密文在每次更新时都是全新随机的，敌手不能区分更新后的签密文和一个全新生成的签密文，因此他不能注意到这个改变.

对所有连续的时期e和e+1，敌手不知道链接的令牌Δe+1，签密文在完全独立密钥下是全新签密，换言之，即使A腐败从时期e开始的密钥，这也不会帮助他从时期e+1 腐败的签密文中获得信息，反之亦然.

3.3.3 数据完整性

引理1如果一个签密算法的导出签名算法SIG 是INT-PTXT 安全的，那么用EtS 方式构造的签密算法在上述安全模型中是INT-PTXT 安全的.

证明:该引理的证明由Dent 等人[7]所给出，本文在这里不再赘述，因此可以将USIGE 的INTPTXT 安全性归约到导出签名算法SIG 的INT-PTXT 安全性.

定义7导出签名算法SIG 定义如下:

并将区间[e-，e+]定义为一个窗口，集合E[1，e*]|e/*∪K*∧e′/*，e′*，∀e ＜e′≤e*}是空集(如果它不是空集，那么它有一个最大值元素).

命题2设A是一个能够在INT-PTXT 实验中于时期0＜e*≤emax产生一个伪造的有效敌手，那么存在一个最大整数0＜e-≤e*和一个最小整数e*＜e+≤emax使得A从向谕言机发出的查询中:

· 不能获得令牌Δe-和Δe+，

· 不能获得时期e-≤e ＜e+的私钥ske，

· 可以获得时期e-＜e ＜e+的所有令牌Δe.

通常称区间[e-，e+] 为窗口，显然上述两个命题为真命题，那么很容易可以得到下面这个命题.

命题3令Σ 是一个基于BLS 签名的消息独立可更新签名算法，那么有:

· 对每个(sk，pk)←SIG.Setup(λ)，sk·Δ(Δ←Qp) 和由(sk′，pk′)←SIG.Setup(λ) 得到的sk′分布相同.

· 对每个(sk，pk)←SIG.Setup(λ) 和Δ，有(sk·Δ，pkΔ)SIG.Setup(λ).[6]

引理2 令Σ(KeyGen，Sign，Adapt，Verify) 是一个BLS 签名算法，其中Adapt 算法被定义为(pkΔ，σΔ)←Adapt(pk，θ，σ，Δ)，如果Σ 是INT-PTXT 安全的，那么可更新的签名算法S 是INT-PTXT安全的.

证明:由上述三个命题可知，将可更新签名算法S 的INT-PTXT 安全性归约于Σ 的INT-PTXT安全性时，挑战者将会归属于时期e-.由于在时期e-使用挑战者的签名谕言机Oσ，我们必须回应时期e*和邻近时期的签名查询，以及从旧时期到e*和从e*到新时期的更新查询，此外，必须为敌手的腐败查询提供密钥和令牌.通过命题2 我们知道为使敌手是有效的并排除平凡的伪造，需要有A没有查询令牌Δe-和Δe+并且未腐败任何密钥但腐败所有窗口时期令牌的最大时期1≤e-≤e*和最小时期e*＜e+≤emax.借助Klooβ 等人[15]的技术进行优化，因此与其猜测挑战时期e*和窗口的左右端，不如只用猜测e-和e+的边界，仅仅将挑战者和该区间里的某时期联系起来，这样可以降低归约损失.

在窗口之外，即对于直到e--1 和e+之后的时期，我们将在模拟中表现得像在原始游戏中一样，特别是选择和腐败所有密钥和更新令牌(Δe+除外).对于窗口内的所有时期，策略如下: 我们不知道与这些时期相关的密钥，但它们是通过为窗口中的每个时期ei选择一个随机令牌Δei设置的，就像在真正的Next 算法中一样.然后，对从e-开始的窗口中每个时期ei，设置相应的公钥为pkei(对所有e-＜ei ＜e+).现在，对于窗口内消息m和时期ei的任何签名查询，我们向和时期e-相关的Σ 挑战者查询m，并在之后使用Σ.Adapt 算法以获得窗口内时期ei对消息m的签名.值得注意的是，由于Σ 的自适应属性，因此来自SIG.Sign 和Σ.Adapt 的签名分布相同，这对A来说是无法区分的.对于那些更新令牌被腐败的时期，谕言机OUpdσ会像在原始游戏中一样;对于其余的时期，即e-和e+，当被要求更新(m，σe--1) (或(m，σe+-1)) 时，我们向与e-相关的Σ 挑战者查询m(或使用ske+生成一个新的签名)，并将其返回给敌手.同样，由于Σ 的自适应属性，以及新生成的签名和更新后签名的分布相同，这是无法区分的.现在，如果A输出时期e*的一个有效伪造(m*，)，如果e*e-我们可以直接输出它;否则使用Σ.Adapt 调整伪造使其倒退到时代e-并输出它.

考虑下面一系列游戏:

引理3BLS 签名算法Σ 在CDH 假设下是INT-PTXT 安全的[14].

引理3 的证明由Boneh 等人[14]给出，本文这里不再赘述.

综上，可以得到定理3.

定理3(USE 是INT-PTXT 安全的) 可更新的签密算法USE 在CDH 假设下具有数据完整性.

4 性能分析

表1 给出了本文所设计可更新签密算法USE 在计算开销方面和存储开销方面的性能分析，计算开销主要考虑指数运算和配对运算，它们是算法中的主要运算.用texp、tpair和thash分别表示指数运算、双线性对运算和计算hash 函数的时间，|G| 表示群G中元素的长度，表示群中元素的长度.

表1 计算和存储开销等性能分析Table 1 Performance analysis of computational and storage overheads

5 总结与展望

本文主要围绕如何同时解决公钥场景下云数据存储的机密性和完整性问题展开研究，提出了可更新签密的概念，为其搭建了安全模型，并基于BLS 短签名和ElGamal 加密构造出一个双用户模型下的密文独立的可更新签密算法.该算法采用“加密后签名” (EtS) 的方法，继承了导出签名算法的认证性.其中加密部分基于ElGamal 加密算法，利用了代数结构的底层群运算，而非使用密钥同态伪随机函数[16];签名部分则是基于BLS 短签名算法，相比于ECDSA 签名或Schnorr 签名，BLS 签名不仅可以解决前面两者存在的问题(如难以进行签名聚合、通信开销较大等)，而且相比于签名长度为320 比特的ECDSA 签名和512 比特的Schnorr 签名，签名长度更短，仅为160 比特，性能更优良.同时，该算法不仅支持签密文的更新，以降低密钥泄露的风险和影响，而且还提供数据完整性，以防止云服务提供商随意篡改或插入密文.此外，还额外增添了认证性，以确保数据的确是由发方上传的.最后，基于计算Diffie-Hellman 假设和判定Diffie-Hellman 假设，在安全模型下证明了该算法具有良好的密文不可区分性、更新不可链接性以及数据完整性.

虽然本文提出的可更新签密算法同时达到了云存储数据的机密性和完整性，但仍有进一步探索和改进的空间.首先，本文仅在双用户模型下考虑可更新的签密算法，并没有考虑当多用户[17，18]存在时的情况.其次，本文的机密性仅实现了CPA 安全，并未能实现CCA 安全[4，19]，而Klooβ 等人[15]虽然已经提出了具有(R)CCA 安全性的算法，但其算法过于冗杂，从而效率相对较低，因此如何构造一个既高效又安全的算法仍是未来的一个研究方向.最后，本文分析的所有算法都允许从密钥中推断令牌，并允许对密文和密钥进行双向更新，而理想的可更新加密算法应该只允许对密文进行单向更新.Nishimaki[20]和Jiang等人[21]的研究都表明密钥更新的方向性对可更新密码算法安全性具有深刻影响，如何构建一个密钥无向或后向泄露单向更新[22]、密文单向更新的可更新签密算法也是一个值得深入研究的问题.