一种基于同态签名的可验证联邦学习方案*

赵家雪，苏 铓，侯金鹏，付安民，

1.南京理工大学 网络空间安全学院，江阴214443

2.南京理工大学 计算机科学与工程学院，南京210094

1 引言

深度学习技术已经被广泛应用于计算机视觉[1]、语音识别[2]、医疗预测[3]、自动驾驶[4]等多个领域并取得了重大突破.深度学习需要收集不同来源的大量数据，然而这些数据可能包含用户的敏感信息，例如医疗系统中患者的用药情况和诊断结果.由于患者关注自己的隐私安全，拒绝向第三方服务提供商共享自己的医疗数据，进而阻碍数据收集和深度学习过程.近年来，个人数据泄露事件层出不穷，各个国家都开始出台数据隐私保护相关的法律法规，如欧盟2018 年5 月25 日出台的《通用数据保护条例》(General Data Protection Regulation，GDPR)[5].个人隐私保护意识和严格的法律法规导致训练数据的收集愈发困难，致使深度学习面临着巨大的挑战.

联邦学习[6]作为一种新兴的分布式训练系统受到越来越多的关注，它由一个服务器和多个用户组成，用户终端可以是手机、传感器、笔记本电脑.在联邦学习中，这些用户使用私有数据集训练本地模型，在每次本地训练结束时将模型参数上传到服务器.服务器接收到在线用户的模型参数后，聚合所有用户的本地模型参数并对聚合结果进行广播.每个用户根据接收到的聚合结果更新本地模型，这样的训练过程一直持续到模型收敛为止.这种分布式训练方式避免用户将自己的数据暴露给其他参与方，可以保护用户参与训练时的隐私.同时多用户的协同训练，增大了训练数据量和样本多样性，有助于提高用户训练的模型精度.

联邦学习虽然可以解决隐私直接泄露问题，但研究表明，攻击者仍然可以利用用户上传的模型参数间接获取标签、成员等敏感信息[7-10].为了解决这类问题，一些专注于隐私保护联邦学习的方案被提出.Ma等人[11]提出了一种具有高计算和通信效率的差分私有拜占庭鲁棒联邦学习方案，有效地防止拜占庭参与者发起的对抗性攻击，并通过shuffle 模型中的一种新的聚合协议实现了不同的隐私保护.Fang 等人[12]基于改进的ElGamal 同态加密保护模型参数，同时利用秘密共享技术将加密密钥拆分给不同用户保存.服务器只有勾结多个恶意用户，才能恢复密钥，获取模型参数.方案提高了服务器的攻击难度，保障了用户模型的安全性.Bonawitz 等人[13]通过密钥协商和秘密共享，设计了一种高效的双掩码协议来实现高维数据的安全聚合.方案允许用户在训练过程中动态退出，从而避免用户离线导致的解密错误，确保聚合结果的正确性.

上述具有隐私保护的方案均不支持验证从服务器返回结果的正确性.在某些非法利益的驱使下，恶意的服务器会向用户返回不正确的聚合结果，例如服务器会采用简单不准确的模型来压缩原始模型，以降低自己的计算成本.另外，恶意服务器还可以分析用户上传数据的统计特征，精心伪造聚合结果[14]，诱导用户发布更多额外的敏感信息.因此，在保护用户数据隐私的同时，有效地验证服务器聚合结果的正确性是十分重要的.Xu 等人[15]提出了第一个在神经网络训练过程中支持验证的隐私保护方案VerifyNet.方案采用同态哈希函数和伪随机函数，实现用户对聚合结果的验证.然而验证协议是基于零知识证明设计的，用户需要为每个维度的参数计算验证信息，导致验证通信开销和计算成本太大，无法应用于移动设备数量庞大的联邦学习.Guo 等人[16]将线性同态哈希与承诺方案结合起来，提出了一种快速验证的联邦学习可验证聚合协议.该方案实现了聚合结果正确性验证的通信开销与模型参数的维度无关.然而为确保在部分用户退出训练时在线用户仍能进行验证，该方案将同态哈希结果进行秘密共享，增加了用户验证的通信开销.Zhou 等人[17]利用同态哈希和签名设计了一种不可追溯的、低通信的验证方案.该方案实现了验证通信开销与模型参数维度和用户数量无关，然而由于用户在验证时首先要验证其他用户的签名，由此增加了验证的计算开销.此外，文献[16，17] 中用户都需要在服务器聚合前向其他用户提供承诺或签名，如果有新用户加入训练，由于新用户并没获得上一轮参与训练用户的承诺或签名，则无法对聚合结果进行验证.Zhang 等人[18]利用中国剩余定理和Paillier 同态加密来保护数据隐私，并引入双线性聚合签名技术来实现对聚合梯度的验证.在Fu 等人[19]提出的方案中，使用基于拉格朗日插值的精心设置的插值点来验证聚合梯度的正确性，该方案可以有效防止模型参数的泄漏.

联邦学习面临隐私泄露和聚合结果伪造等问题，尽管部分研究已经实现了联邦学习的隐私保护，同时允许用户对聚合结果进行正确性验证.但目前可用的验证方案不能同时实现快速且低通信的验证，并且无法支持动态用户对上一轮聚合结果的验证，很难应用到用户数量庞大、动态参与训练的实际场景.为此，本文提出了一种可验证的联邦学习方案，既保护了数据在聚合阶段的隐私，也实现了高效的、低通信的验证协议.本文首先使用密钥协商和公开可验证秘密共享协议保护用户本地模型的隐私，并解决用户动态退出的问题.然后基于非对称可编程哈希函数和同态签名实现可验证方案，支持任意持有公钥的用户对聚合结果正确性的验证.

本文的主要贡献如下:

(1) 本文利用密钥协商和公开可验证秘密共享协议实现了一种双掩码安全聚合协议，以此保护联邦学习过程中用户本地模型参数，防止用户隐私泄露.该协议允许训练过程中超过半数的用户退出，避免用户离线导致服务器解密失败.同时服务器可以公开验证用户分发的共享和用于重构的共享是否有效，确保用户共享行为诚实，进一步提升解密结果的正确性.

(2) 本文首次将同态签名引入联邦学习，实现了一种高效、低通信的可验证的联邦学习方案.同态签名方案可以极大化地降低验证阶段的通信开销，同时支持新用户对聚合结果的验证.此外，方案采用由非对称可编程哈希函数构建的同态签名，使得该验证方案具有更短的验证公钥长度，减少了用户的存储开销，更适用于联邦学习中资源受限的移动设备.

(3) 本文从理论上全面分析了方案的安全性，即使多个恶意用户合谋，恶意用户也无法获得诚实用户本地模型的任何有用信息.此外，服务器在没有签名私钥的情况下无法伪造同态签名，方案确保了用户可以验证聚合结果的正确性.本文在实际数据上进行了实验，结果表明本文方案验证时的计算开销和通信开销均处于较低水平，实现了快速且低通信的验证.整体开销结果也表明完整方案并未对用户本地训练产生显著影响，证明本文方案是一种高效可行的联邦学习方案.

本文其余部分结构: 第2 节介绍方案所需的预备知识.第3 节介绍方案中的符号定义、系统框架和威胁模型.第4 节给出方案的具体细节.第5 节对方案进行安全性分析.第6 节对实验结果进行分析.第7 节进行总结和讨论.

2 预备知识

2.1 公开可验证秘密共享

与Shamir 门限秘密共享[20]相比，公开可验证秘密共享(publicly verifiable secret sharing，PVSS)是一种安全性更高的密码学协议，可以保证任何人均能公开地验证共享正确性.文献[21] 基于非交互零知识证明和里德-所罗门码构建了一种PVSS 协议，具体包含以下算法:

(1) PVSS.Gen(bgp)→(sk，pk): 输入非对称双线性群组bgp(q，G1，G2，GT，g，h，e)，g和h分别是群G1和G2的生成元.设置加密私钥sk←Zq，计算公钥pkhsk，返回加密密钥对(sk，pk).

2.2 非对称可编程哈希函数

本文使用非对称可编程哈希函数(asymmetric programmable hash functions，APHF)[22]生成较短的公钥，构造适用于联邦学习的同态签名方案.设bgp(q，G1，G2，GT，g，h，e) 是非对称双线性群组，g和h分别是群G1和G2的生成元.[X] 表示集合{1，2，···，X}，令x非对称可编程哈希函数H:[X]→G1由三个多项式时间算法(H.Gen，H.PriEval，H.PubEval) 组成:

(1) H.Gen(bgp)→(sek，pek): 输入非对称双线性群组bgp，对于i1，2，···，x，随机采样αi，βi ←Zq，计算Aigαi，Bihβi.设置sek，pek，返回(sek，pek).

(2) H.PriEval(sek，n)→Y: 输入sek 和变量[X]，n可以由一对整数(i，j)[x]×[x] 表示，计算并返回Y1.

(3) H.PubEval(pek，n)→ˆY: 输入pek 和变量[X]，且n(i，j)，计算并返回e(Ai，Bj)e(H(n)，h).

3 形式化定义

3.1 符号定义

本文方案中使用的部分符号定义如表1 所示.

表1 相关符号定义Table 1 Definition of symbles

表2 威胁模型实体定义Table 2 Definitions of threat model entity

3.2 联邦学习系统框架

联邦学习要求多个用户使用本地数据合作训练一个共享的全局模型参数ω*.如图1 所示，本文的联邦学习系统由可信机构、服务器和N个用户组成，其中每个用户n都存在一个独立同分布(independently identical distribution，IID) 或者non-IID 数据集Dn，则|D|具体地，可信机构为每个用户创建密钥后就下线.用户n使用损失函数Ln(Dn;ωn) 训练数据集Dn，其中ωnRL表示模型可训练的参数.服务器上的全局模型的损失函数为L(D;ω)，联邦学习所面临的优化问题为:

图1 系统框架Figure 1 System architecture

为了最小化上述目标，服务器和用户需要执行以下步骤:

(1) 初始化: 服务器向每个用户发送初始化的全局模型参数ω0.

(2) 本地训练: 用户n在本地数据集Dn上使用优化器(如SGD) 对全局模型进行本地训练.训练结束后，用户n向服务器上传本地模型参数

(3) 全局聚合: 服务器收集用户上传的本地模型参数并使用聚合方法聚合生成一个新的全局模型，即wk+1之后服务器将更新的全局模型参数wk+1发送给下一轮参与训练的用户.

3.3 威胁模型

以往方案[14-16]定义了一种诚实但好奇的威胁模型.服务器和用户诚实执行聚合协议，同时允许服务器与多个用户合谋推断用户隐私，但不允许服务器与用户合谋伪造聚合结果.然而，用户也可以与服务器合谋伪造聚合结果，进一步推断用户隐私，那么上述方案定义的限制实际并不可行.为此本文定义了一个新的威胁模型，该威胁模型具有可信机构、诚实用户、恶意用户和恶意服务器.具体来说，可信机构是完全可信的，不会泄露任何用户的密钥.诚实用户按照商定的协议，遵循完整的方案流程进行操作.恶意用户试图独立或与其他恶意用户合谋推断诚实用户隐私，甚至偏离聚合协议，上传虚假的共享破坏服务器解密结果的正确性.恶意服务器可以按照商定好的聚合协议获得正确的聚合结果，但会独立推断用户隐私，并伪造聚合结果以欺骗用户.与以往方案相比，本文定义的恶意威胁模型允许恶意用户破坏解密结果，更加贴切实际场景，能够提供更高的安全保障.此外，在以往方案定义的威胁模型下，本文方案同样安全.

4 隐私保护可验证联邦学习

正如前文所述，在联邦学习中面临着两个重要问题.第一个问题是如何保护用户的本地模型，防止攻击者利用本地模型参数间接获取用户的隐私信息.另一个问题则是如何验证服务器返回全局模型参数的正确性，防止服务器伪造聚合结果.为了解决这两大挑战，本文采用双掩码安全聚合协议，对本地模型参数进行加密处理，提升数据机密性，防止用户隐私信息的泄露.另外采用同态签名方案，实现用户对全局模型参数的验证，保证聚合结果的正确性.通过以上解决方案，可以在联邦学习中克服隐私泄露和数据伪造等潜在威胁，确保数据的安全性和可靠性.

4.1 双掩码安全聚合协议

文献[15] 提出了一种双掩码聚合协议保护用户本地模型参数，同时支持用户在训练过程中的动态退出.假设系统中用户是有序的，且使用同样大小的数据集进行本地训练，用户n可以对本地模型参数ωn进行如下形式的加密:

如果一个用户在上传公钥后退出协议，或没有及时上传加密参数，由于其他用户在加密时添加了与该用户相关的随机数，导致服务器在聚合时不能抵消掩码，从而无法计算正确的聚合结果.为此每个用户n采用Shamir 门限秘密共享，将协商私钥rskn共享给其他用户.当用户n的掩码无法抵消时，服务器要求超过阈值数量的用户提交rskn的秘密共享.在重构出rskn后，可以恢复用户n与其他用户m的随机数PRG(sn，m)，并最终在聚合结果中移除用户n的掩码.

用户n额外添加一个噪声的随机掩码PRG(βn) 保护本地参数ωn.这是因为在某些情况下，用户n会延迟将数据上传到服务器，这将导致服务器错误地判定用户n退出训练，从而要求其他在线用户上传rskn共享以删除掩码.然而当用户n成功将ˆωn上传到服务器时，由于服务器可以重构rskn、删除掩码来获得用户本地模型参数ωn，恶意的服务器也可以通过谎报用户退出进而学习用户本地模型参数ωn，βn也需在上传ˆωn前共享给其他用户，使得服务器可以在聚合时消除掩码PRG(βn).

然而该方案不能应对恶意用户的主动攻击.由于用户共享时输入和输出是不可见的，Shamir 门限秘密共享无法确保用户上传了正确的共享，如果存在一些恶意用户故意偏离协议，将影响秘密的正确性和安全性.为此本文采用PVSS 提升秘密共享的安全性和可靠性，根据2.1 节中的算法，用户n使用PVSS.share将rskn和βn进行共享，服务器可以通过PVSS.Verify 验证用户n生成共享的有效性.此外，在用户m解密用户n的共享后，服务器可以验证用户m提交的解密共享的正确性，确保秘密可以被正确重构，有效避免恶意用户的影响.

其中U2是提交共享的用户集合，且U2⊆U1.

服务器计算的聚合结果为:

其中U3是提交加密参数的用户集合，且U3⊆U2⊆U1.U2U3是在U2中但不在U3中的用户集合.

服务器在解密阶段需要重构U2U3中用户的私钥和U3U4中用户的噪声，其中U4是提交解密共享和自身噪声的用户集合，U3U4是在U3中但不在U4中的用户集合.诚实的用户永远不会泄露同一用户的两种共享.服务器可以删除退出用户的掩码和在线用户的噪声，得到正确的聚合结果，但始终无法获取用户原始的本地模型参数.单轮双掩码安全聚合协议框架如图2，该协议实现了在训练过程中保护用户的数据隐私，并支持用户在训练过程中因某种原因退出.然而该聚合协议并不支持用户验证服务器的聚合结果，为此本文利用同态签名技术，与双掩码安全聚合协议兼容，允许每个用户在可接受的开销下验证服务器聚合结果的正确性.

图2 单轮双掩码安全聚合协议框架Figure 2 Singl-round double-mask secure aggregation protocol framework

4.2 同态签名验证方案

本文使用基于APHF 并结合BLS 签名[26]的同态签名算法，实现了公钥更短的联邦学习高效验证方案.已知 BLS 签名包含三个多项式算法 BLS=(BLS.Gen，BLS.Sign，BLS.Verify)，F:K×{0，1}*→Zq是一个密钥空间为K的伪随机函数.该同态签名方案支持N个用户对L维消息签名，同时可以进行部分离线计算实现有效验证.设H(H.Gen，H.PriEval，H.PubEval) 和H′(H.Gen′，H.PriEval′，H.PubEval′) 是两个APHF，使得H: [N]→G1，H′: [L]→G1.完整的同态签名方案包含以下算法:

(1) HS.Gen(bgp)→(hsk，hpk):输入非对称双线性群组bgp.创建BLS 算法签名密钥对(sk′，pk′)←BLS.Gen(bgp).在伪随机函数F:K×{0，1}*→Zq密钥空间中选择两个随机种子K，←K.生成两组APHF 的密钥对(sek，pek)←H.Gen(bgp) 和(sek′，pek′)←H.Gen′(bgp).设置hsk(sk′，K，，sek，sek′) 和hpk(pk′，bgp，pek，pek′)，返回同态签名密钥(hsk，hpk).

(2) HS.Sign(hsk，ω，n，Δ)→σn: 输入签名私钥hsk、模型参数ω、用户标识n和标识符Δ，生成同态签名具体包含以下几个步骤:

· 利用伪随机函数推导出z ←FK(Δ)，计算Zhz.

· 将Z与标识符Δ 绑定，计算σΔ←BLS.Sign(sk′，Δ|Z).

· 推导r ←FˆK(Δ|n)，设置Rgr并计算

· 返回同态签名σ(σΔ，Z，R，S).

(3) HS.Eval(Σ，U)→σ: 输入一组签名Σ{σm}m∈U，其中σm(σΔ，m，Zm，Rm，Sm)，以及用户集合U.随机选择一个，设置σΔσΔ，m，ZZm.计算

返回同态签名σ(σΔ，Z，R，S).

(4) HS.Verify(hpk，ω，σ，U，Δ)→Bool: 输入验证公钥hpk、模型参数ω、同态签名σ、用户集合U和标识符Δ.首先运行BLS.Verify(pk′，Δ|Z，σΔ)，验证σΔ是否为标识符Δ 和Z的有效签名.如果无效，停止并返回False.否则，当且仅当满足下列等式返回True:

为实现高效验证，我们观察到H.PubEval 和H.PubEval′可以预先计算出结果后被重复使用.为此HS.Verify 算法可分为离线阶段和在线阶段.

(1) HS.VerPre(H，H′，hpk，U，L)→输入非对称可编程哈希函数H，H′，验证公钥hpk、用户集合U和消息维度L.对于，计算HmH.PubEval(pek，m)，H{Hm}m∈U对于，计算H.PubEval′(pek′，l)，H′，返回hpkp(pk′，bgp，H，H′).

(2) HS.EffVer(hpkp，ω，σ，U，Δ)→Bool: 该算法和HS.Verify 相同，只是公式(3)计算修改为:

结合双掩码安全聚合协议，使用同态签名算法进聚合结果正确性验证的流程如图3.用户n可以在阶段1 之前通过HS.VerPre 算法离线预处理部分结果.在训练得到本地模型参数ωn后，使用HS.Sign 算法对ωn签名，并将签名σn和加密参数一起发送至服务器.服务器聚合所有签名，并在解密聚合参数后，将聚合签名σ和全局参数ω发送给用户.用户使用HS.EffVer 算法就可以快速验证服务器返回的聚合结果是否正确.

图3 单轮同态签名验证方案框架Figure 3 Single-round homomorphic signatures verification scheme framework

5 安全分析

在本文的威胁模型中，允许恶意用户偏离协议上传虚假共享，但它们无法破坏服务器解密结果的正确性.同时允许t-1 个恶意用户合谋攻击诚实用户隐私，但它们仍对诚实用户的本地模型一无所知.为证明聚合协议的安全性，给定一个由多方组成的子集W ⊆U，W中各方的联合视图可以表示为一个随机变量证明涉及的其他符号与上文定义相同.

首先定理1 和定理2 保证PVSS 的可验证性，使得服务器可以验证用户的共享是否合法和正确，有效地避免恶意用户的虚假共享对解密结果的产生影响.

定理2如果V中的用户m在PVSS.Dec 阶段通信了错误的解密共享服务器在PVSS.Recon 阶段将以1-ϵ的概率检测到这一情况，其中ϵ是证明DELQ 的完备性误差.

上述定理证明与文献[21] 中定理2 和定理3 的证明相同.通过PVSS 的共享验证可以筛选掉恶意用户上传的共享，确保解密结果的正确性.再通过定理3 证明方案可以防御t-1 个恶意用户(不包括服务器)的合谋攻击.

定理3对于所有的t，λ，ωU，W ⊆U，|U|≥t，且U4⊆U3⊆U2⊆U1⊆U，存在一个PPT 模拟器SIM，其输出与的输出无法区分，即

证明:由于排除了服务器的参与，集合W中各方的联合视图不依赖于不在W中的其他用户的输入.因此，模拟器SIM 可以使用恶意用户的真实输入来生成完美的模拟，但将诚实用户的输入替换为假数据(例如随机生成的数字).本文强调在W中用户的模拟视图与真实视图的输出是无法区分的.更具体说，在阶段3 中，模拟器SIM 通过使用随机数(例如0) 而不是使用真正的模型参数，为所有诚实的用户(不在W中) 生成加密参数此外，我们注意到服务器在阶段3 中只发送所有在线用户的集合，而不是特定的的实际值，这意味着恶意用户无法识别服务器返回的聚合结果是否基于诚实用户的真实模型参数.因此，W中用户的模拟视图与真实视图的输出是无法区分的.

定理4设BLS 方案是一个不可伪造的签名方案，F是一个伪随机函数，G是一个双线性群生成器，使得H具有(1，γ，ϵ)-可编程伪随机性，且H′是(poly，0，1，γ′，δ′)-可编程的[22].由于FDHI 的假设成立，同态签名是不可伪造的.

证明:通过游戏证明定理4，定义一个PPT 的敌手A和一个PPT 的挑战者C，如果A能够以ϵ的优势赢得游戏，那么C可以使用A以ϵ的优势解决FDHI 问题.C接收到一个FDHI 实例并按如下方式工作:

初始化:挑战者C选择一个随机索引[Q]，Q是敌手A查询的不同用户集合数量.其次，C运行可编程伪随机函数H的陷门生成算法(td，pek)←H.TrapGen(1λ，bgp，g，g，h，hz)，(poly，0，1)-可编程函数H′的陷门生成算法(td′，pek′)←H′.TrapGen(1λ，bgp，g，g，h，hz).

C最终生成BLS 方案的(sk′，pk′)，设置hpk(pk′，pek，pek′)，保存sk′，td，td′，将hpk 发送至A.

签名查询:设k ←1 是A查询的用户集合数量的计数器.对于每一个新查询的用户集U，C创建一个(n，ω，σ) 的列表TU，它收集A在用户集合U中查询的所有用户标识/消息以及生成的相应签名.

每当查询第k个用户集合Uk时，C做以下操作:如果kμ，则随机采样ξμ ←Zq，计算Zμ(hz)ξμ并保存Zμ，ξμ;如果k/μ，C随机采样ξk ←Zq，计算Zk(hv)ξk并保存Zk，ξk.所有{Zk}k∈[Q]都是G2中随机的，它们与通过伪随机函数F计算得到的结果分布完全相同.

给定一个签名查询(U，n，ω)，使得UUk是第k个用户集合.C首先计算←BLS.Sign(sk′，Uk，n)，然后执行以下操作:

返回签名σ(σUk，Zk，Rn，Sn) 至A.该签名满足真实的分布，因为Rn是均匀分布的G1元素，并且

返回签名σ(σUμ，Zμ，Rn，Sn) 至A.对于Sn我们有

返回(W，W′) 作为FDHI 假设的解，即W′W1/z，可以观察到

综上所述，如果A赢得了游戏，那么C就可以解决FDHI 假设，从而证明该同态签名不可伪造.

6 性能分析

本文方案基于双线性映射的开源库pypbc，使用Python 语言实现.实验环境为Intel(R) Core(TM)i7-6700 CPU @3.40 GHz 上的VMware 虚拟机，分配2 个CPU 核心和4 GB 内存，操作系统为Ubuntu22.04.实验模拟一个服务器和500 个用户，对10 000 维的神经网络模型进行联邦学习训练.

6.1 功能对比

如表3 所示，将本文方案的功能和文献[14—17] 进行比较.具体来说，文献[14—17] 和本文方案均实现了对用户数据的隐私保护，且支持训练过程中用户的动态退出.与文献[14—16] 相比，本文方案进一步提升了隐私保护共享阶段的安全性，抵抗恶意用户的主动攻击.文献[17] 采用差分隐私实现隐私保护，不涉及秘密共享的安全性.此外，文献[14] 不支持用户对聚合结果的验证功能，文献[15—17] 均支持用户对聚合结果的验证功能，然而文献[16，17] 无法支持动态用户对上一轮聚合结果的验证.与这些方案相比，本文方案不仅可以保护数据隐私，同时支持任意持有公钥的动态用户对聚合结果进行验证.

表3 功能对比Table 3 Comparison of functions

6.2 用户验证开销对比

文献[16，17]在验证聚合结果时均需要为每一参数维度分配验证公钥，由此增加了用户的存储开销.本文方案采用APHF 构建的同态签名对聚合结果进行验证，可以将公钥长度从O(N+L) 降低到其中N和L分别是用户数量和参数维度.

在本文方案中，用户验证聚合结果时需要执行多次哈希查询和双线性映射，从而增加计算开销.为了提高验证效率，本文方案可以将验证过程分为离线的预处理和在线的单轮验证两个阶段.表4 给出了500个用户训练不同维度的模型参数、每个用户验证时各阶段的计算开销和完整验证的总计算开销.可以看出，随着参数维度的增长，用户验证时的计算开销呈明显的线性增长趋势.此外，两个阶段几乎各占完整验证计算开销的一半.为此用户可以在训练正式开始前，离线进行预处理计算，并在每轮训练中重复利用预处理结果进行验证，有效降低用户单轮验证的计算开销.

表4 用户验证计算开销Table 4 Computation overhead for user verification

由于文献[14] 不具有验证功能，文献[15] 的验证开销很大程度依赖于参数维度，不适用于规模庞大的联邦学习.为此，本文仅与文献[16，17] 对比用户单轮验证的计算开销，同时还针对不同的参数维度和用户数量进行了单轮验证计算开销的测量.如图4 所示，随着参数维度和用户数量的增长，三个方案中用户验证时的计算开销均呈现出线性增长趋势.值得注意的是，用户数量对文献[17] 中用户验证时的计算开销有着显著影响，这是因为用户需要验证所有在线用户的签名，从而增加了计算开销.而文献[16] 和本文方案受用户数量影响较小.在同一参数维度下，本文方案用户验证时仅比文献[16] 慢100 ms 左右.通过采用离线预处理的方法，本文方案在降低验证公钥长度的前提下，实现了与文献[16] 近乎相当的单轮验证计算效率.

图4 用户单轮验证计算开销对比Figure 4 Comparison of communication overhead for user verification per round

图5 给出了本文方案与文献[16，17] 用户单轮验证通信开销的对比结果.

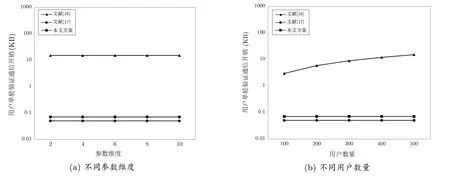
图5 用户单轮验证通信开销对比Figure 5 Comparison of communication overhead for user verification per round

从图5(a)可以看出，三个方案用于验证的通信开销都与参数维度无关.从图5(b)可以看出，文献[16]用于验证的通信开销受用户数量的影响.这是因为用户需要将哈希计算结果秘密共享给其他用户，确保用户退出时在线用户仍能进行验证.因此用户数量越多，用于验证的通信开销也越大.在文献[17] 和本文方案中，用户只需要向服务器通信一次签名，无需额外的通信开销，为此将文献[16] 中的验证通信开销降低了两个数量级.与文献[17] 相比，同态签名的长度大于普通签名，所以本文方案用于验证的通信开销略高，但几乎不会对用户的整体通信产生影响.

6.3 整体方案对比

本文还与文献[16，17] 对比了单轮训练时的整体开销.从表5 可以看出，文献[17] 的整体开销要优于文献[16] 和本文方案，这是因为该方案使用差分隐私实现隐私保护，避免了秘密共享所需的开销.但从图6 可以看出，随着用户退出率的增大，文献[17] 的全局模型精度逐渐下降.这是因为在用户退出后，服务器计算聚合结果没有完全消除噪声，从而影响了全局模型精度.而文献[16] 和本文方案均使用双掩码和秘密共享实现隐私保护，完全消除掩码对聚合结果的影响，确保全局模型的精度.

图6 全局模型精度Figure 6 Global model accuracy

表5 单轮整体开销Table 5 Total overhead per round

相较于文献[16]，本文方案使用PVSS 实现了双掩码安全聚合协议，用户计算开销略高，表明PVSS和同态签名不会对用户计算开销产生显著影响.此外，尽管PVSS 会增加用户的通信开销，但是本文同态签名方案大大降低了用于验证的通信开销，使得本文方案整体的通信开销低于文献[16].

文献[16] 中，服务器还需额外通信哈希计算结果的秘密共享，为此通信开销高于本文方案.然而本文方案中服务器的计算开销远高于文献[16]，这是因为方案采用PVSS 提升共享数据的安全性，服务器需要验证用户提交共享数据的正确性，产生了额外的计算开销.在本文实验环境中，服务器依次验证每个用户的共享，严重影响了计算效率.在实际应用场景中，可以采用异步并行的训练方法，对多个用户的共享同时验证，提高服务器的处理能力，缩短验证时间.

综上所述，本文方案对服务器提出了更高的要求，但也进一步提升了联邦学习的安全性.本文方案不会显著影响用户的整体开销，在确保全局模型高精度的前提下，实现了更安全的数据聚合和高效的聚合结果验证，适用于移动设备数量庞大、资源受限的联邦学习系统.

7 总结

本文构建了一种可验证的联邦学习方案，首先采用双掩码协议对用户模型参数进行加密，同时使用公开可验证秘密共享构建双掩码安全聚合协议，提高了数据共享的安全性，确保解密结果的正确性.其次，使用非对称可编程哈希函数构造的同态签名方案，降低了用于验证的公钥长度，确保任意持有公钥的动态用户可以对聚合结果进行正确性验证.本文在理论上全面分析了方案的安全性，同时在实际数据上进行了实验，证明了方案的高效可行性.通过对用户单轮训练时的验证开销和整体开销进行分析，证明本文方案可以快速进行聚合结果验证，同时对验证的通信开销进行了有效的优化，完整的聚合和可验证方案也不会显著影响联邦学习中用户的训练过程.本文方案的实现提高了联邦学习训练的安全性，同时保证了用户隐私和数据共享的安全性.在未来的工作中，可以权衡方案整体开销和模型精度，研究将差分隐私和同态签名相结合的可验证联邦学习方案.