一种基于不可区分混淆的侧信道防护方案设计*

刘国升，王伟嘉，郁 昱，姚 立，梁浩飞

1.山东大学 网络空间安全学院，青岛266237

2.泉城省实验室，济南250103

3.山东大学 密码技术与信息安全教育部重点实验室，青岛266237

4.上海交通大学 电子信息与电气工程学院，上海200240

1 引言

自从二十世纪九十年代Kocher 等人提出侧信道攻击(side-channel attack)[1]以来，这种技术就一直被认为是密码系统实现过程中的重大安全威胁.侧信道攻击主要利用系统设备在执行过程中产生的功耗等行为信息恢复秘密数据，因此即使是在可证明安全模型下的密码系统也会受到侧信道攻击的威胁[2].当系统设备处理密码算法相关数据与侧信道泄漏(如运行时间、功耗、电磁辐射、故障信息等) 之间存在数据依赖性时，攻击者就可以利用这些泄漏信息恢复密钥等秘密数据[2].侧信道攻击往往给用户或系统带来灾难性的后果，因此需要抵御这种攻击，抵御这类攻击的软硬件措施称为侧信道防护.

侧信道防护的核心是消除或减少攻击者能够利用的具有数据依赖性的侧信息.针对单一侧信道攻击的防护方法有两类思路: 第一类是消除侧信息的数据依赖性，例如在进行有关秘密信息的计算时，使用在各个步骤时间恒定的算法，或使用掩码方案将重要的中间变量随机化，从而难以利用物理设备运行密码算法时产生的能量消耗;第二类是通过掩盖侧信息的某些特征使攻击者无法加以利用，例如使用吸收材料消除声、光、热等侧信息的泄漏，或是引入频率接近的随机干扰源，与密码运行设备同时释放相同类型的侧信息，从而达到侧信道防御的目的.抵抗侧信道攻击还需从系统级层面综合应用多种侧信道防护措施以达到最佳效果.

为了抵抗侧信道攻击，量化密码算法执行过程中的侧信道泄漏以及合理评估密码系统的安全性，密码学家提出了一个重要的研究方向—抗泄漏密码学.在其考虑的场景中，攻击者可以获得有关内部状态的物理泄漏，密码学家需要在此条件下构造出抗泄漏的密码方案，一些满足抗泄漏安全性的方案也随之产生.抗泄漏是指在一定泄漏模型下(计算模型、有界泄漏模型、无界泄漏模型和连续泄漏模型等)，假设攻击者得到部分信息，设备仍然是安全的.在此框架下，许多抗泄漏密码方案相继被提出.例如在公钥加密与数字签名方面，Dachman-Soled 等人[3]用不可区分混淆构造了抗泄漏的公钥加密方案.

不可区分混淆(indistinguishability obfuscation，iO) 是指拥有同样功能性的一类程序被混淆之后变得不可区分的特性.这一理论研究是由Barak 等人[4]发起的，他论证了虚拟黑盒(virtual black-box) 混淆的概念是不可能对所有电路实现的.当Garg 等人[5]给出了第一个不可区分性混淆的候选构造，并在后续的工作[6]中展示了如何在众多密码学上有用的方式中使用这个构造时，iO才被真正重视起来.事实上，今天的iO被广泛认为是“完整的密码学”，能够基本上实现任何密码学任务.

几年前Bartusek 等人[7]提出了一种特殊的候选混淆器，它用于混淆仿射行列式程序.仿射行列式程序(affine determinant program，ADP):{0，1}n →{0，1}是由一个有限域Fq上的方形矩阵元组(A，B1，B2，···，Bn) 和一个评估函数Eval: Fq → {0，1}来描述的，并通过计算Eval(det(A+来对进行0，1}n评估.基于ADP 的候选混淆方案是独一无二的，因为它是迄今为止唯一不依赖任何传统密码学假设(如离散对数或LWE) 的未被打破的候选方案.该候选者的描述也相对简单.此外，目前的量子技术在破解基于ADP 的候选方案方面似乎没有显示出特殊优势.因此，如果LWE在未来被量子算法打破，ADP 的混淆候选方案可能是唯一对抗量子计算机的iO候选方案.

使用ADP 程序模型进行混淆的想法也被用于Bartusek 等人的早期论文中[8]，他们实现了基于可证明的安全性.他们可以实现基于标准密码学假设的可证明的安全性，然而混淆通用程序需要明显不同的想法.所以Yao 等人[9]针对Bartusek 等人的iO候选方案[8]进行了密码分析攻击.他们利用算法中一个随机化步骤的弱点进行攻击，该攻击适用于相当普遍的一类程序，最后还提出了抵抗攻击的合理对策.

本文对这种基于ADP 的iO方案进行了改善.将整体密码算法的ADP 编码拆解成多个部分运算再利用掩码方案进行组合，大大降低了对ADP 进行iO时的运算成本;另外结合侧信道安全性定义，对iO过程进行改善，删除了小偶数噪声和对角矩阵块的构造，加入了ADP 更新算法.改善后的防护方案可以在真实场景中进行应用，然后通过FPGA 功耗测试采集了足够的曲线进行Welch’s t-test，没有明显泄漏，实现了针对侧信道攻击的防护.

2 预备知识

2.1 符号

本文应用到的符号: 使用PPT 表示概率多项式时间;使用粗体大写字母表示矩阵;使用det(A) 表示求矩阵A的行列式;使用|A|表示矩阵A的阶数;使用λ表示安全参数;使用[n]表示集合{1，2，···，n};使用· 表示数乘;使用⊕表示按位异或运算;使用∧表示按位与运算;使用⋙表示循环右移;使用¯x表示二进制对x取反.

2.2 SHA-2

安全散列算法2 (secure hash algorithm 2，SHA-2) 是美国国家安全局研发[10]的密码散列函数算法标准，由美国国家标准与技术研究院(NIST) 在2001 年发布，属于SHA 算法之一，是SHA-1 的后继者.其下又可再分为六个不同的算法标准，包括了: SHA-224、SHA-256、SHA-384、SHA-512、SHA-512/224、SHA-512/256.

NIST 发布了三个额外的SHA 变体，这三个函数都将消息对应到更长的消息摘要.以它们的摘要长度(以比特计算) 加在原名后面来命名: SHA-256、SHA-384 和SHA-512.它们发布于2001 年的FIPS PUB 180-2 草稿中，随即通过审查和评论.包含SHA-1 的FIPS PUB 180-2，于2002 年以官方标准发布.2004年2 月，发布了一次FIPS PUB 180-2 的变更通知，加入了一个额外的变种SHA-224，这是为了符合双密钥3DES 所需的密钥长度而定义[11].

SHA-256 和SHA-512 是很新的散列函数，前者定义一个word 为32 位，后者则定义一个word 为64 位.它们分别使用了不同的偏移量，或用不同的常量，然而，实际上二者结构是相同的，只在循环执行的次数上有所差异.SHA-224 以及SHA-384 则是前述二种散列函数的截短版，利用不同的初始值做计算.

2.3 仿射行列式程序

定义1(分支程序)[9]分支程序(branching programs，BP) 由一个有向无环图G(V，E)、两个特殊顶点s，和一个标记函数φ表示，该函数给E中的每条边分配一个标签(即xi或) 或常数1.其大小表示|V|-1.每个输入分配x(x1，x2，···，xn) 会自然生成出一个无标签的子图Gx，其中每条边，使x满足φ(e).输入x的可达路径是图Gx中的一条有向s-t路径.如果对于每一个x，Gx的顶点出度最多为1，则BP 被称为确定性的.因此，一个确定性的分支程序会计算出函数f:{0，1}n →{0，1}，当且仅当x上可达路径的数量为1 时，f(x)1.

在该定义的基础上可以定义一类新的分支程序，看作是确定性BP 的延展，其每个顶点的出度对所有x都不受1 的限制.这个新概念在混淆ADP 时很有帮助.

定义2(仿射行列式程序)[4]仿射行列式程序(affine determinant program，ADP) 由输入长度n、阶数k和有限域Fq三个参数定义.它由仿射函数M:{0，1}n →和评估函数Eval : Fq →{0，1}组成.其中仿射函数M是在有限域Fq上的n+1 个k×k的矩阵元组M(A，B1，B2，···，Bn)，使得:

对于输入0，1}n，计算ADPM，Eval(x)等价于计算Eval(det(M(x))).

评估函数Eval 一般有以下三种，通常会使用其中一个.

ADP 需要由BP 编码得到.假设有一个大小为l的分支程序，其中每个输入最多有一条可达路径.我们可以将该分支程序表示为一个大小为(l+1)×(l+1)的邻接矩阵.该矩阵用M(x)来表示，其中的每个值都是0、1 或者一些变量(xi或¯xi).由于BP 可以被看做DAG，那么矩阵M(x)中主对角线及以下的值均为0.因此可以将M(x)的主对角线元素修改为-1，并删除最左边一行和最下边一列，得到一个l×l的新矩阵，称之为L(x).对于所有0，1}n，就有det(L(x))f(x).然后定义AL(0)，BiL(1i)-A，其中，0 是指所有输入全为0，1i是指第i位输入为1 而其他位全为0.对于所有的0，1}n，有

从而完成了ADP 的编码，其中使用的评估函数是Eval0.Ishai 等人[12]详细介绍了BP 到ADP 的编码过程.

2.4 不可区分混淆

不可区分混淆 (indistinguishability obfuscation，iO) 是一种概率多项式时间 (probabilistic polynomial-time，PPT) 算法，在保留原功能的同时，将电路C转化成混淆后的电路C′iO(C)，而且对于任何大小相同和功能相等的电路C1和C2，iO(C1) 和iO(C2) 在计算上是不可区分的.严格定义如下:

定义3(不可区分混淆器) 如果满足以下条件，均匀PPT 工具iO就是电路{Cλ}的无差别混淆器:

· (保持强功能性) 对于所有的安全参数N+及所有的，有

· (不可区分性) 对于任意非均匀PPT 区分器D，存在一个可忽略的函数α使以下情况成立: 对于所有的N+，所有的电路对C0，C1，我们有，对于所有的输入x，并且|C0||C1| (其中|C| 表示电路的大小)，如果C0(x)C1(x)，那么

iO是一类强大的密码学原语，在密码学和复杂性理论中有着广泛的应用.过去十年里，有许多iO候选方案被提出，可以分为以下四类:

· 基于多重线性映射(multilinear maps) 的候选方案.最初的iO方案是基于多重线性映射[13-15]建立的，由Garg 等人[5]进行构造.到目前为止，源于Garg 方案的一些变体依旧可以保持安全，但不是可证明安全也没有使用强理论模型.

· 基于简要函数加密(functional encryption，FE) 的候选方案.一些优秀的工作致力于从简洁FE方案中构造iO，这些构造都是基于有根据的假设，包括LPN 假设、配对密码学中的DLIN 假设和NC0中的PRG 假设[16-26].这些构造通过一系列的减法构造出iO，并且利用了基于属性的加密、全同态加密、基于二次函数的FE、同态秘密共享和通用电路等密码学原理.这些方案整体结构复杂，且效率低下.

· 基于非标准格假设的候选方案.Brakerski 等人[27-29]构造了基于强循环安全假设的候选方案，Wee 等人[30]给出了一个基于类循环假设的方案，但Hopkins 等人[31]提供了这两个假设的反例.除此之外，一些工作尝试基于噪声线性FE 构造iO.Devadas 等人[32]在Wee 等人[30]的基础上进行了改进，在简洁的LWE 采样基础上构造iO.这是一个较弱的概念，它提出了一个候选者，其安全性与解多项式方程组的难度有关.这些候选方案的安全性都依赖于非标准的假设.

· 基于仿射行列式程序的候选方案.Bartusek 等人[8]提出了一种特殊的候选混淆方案，它用于混淆仿射行列式程序.仿射行列式程序(affine determinant program，ADP):{0，1}n →{0，1}是由一个有限域Fq上的方形矩阵元组(A，B1，B2，···，Bn) 和一个评估函数Eval: Fq →{0，1}来描述的，并通过计算Eval(det(A+∑i∈[n]xiBi)) 来对0，1}n进行评估.非统一对数空间的计算(用L/poly 表示) 可以转化为多项式大小的ADP.因为NC1⊆L/poly，所以这种ADP 混淆器可以混淆NC1电路，这意味着可以构造出通用的iO.

2.5 掩码技术

掩码技术[33]是指随机化密码设备所处理的中间值来实现侧信道防护的一类技术.在掩码技术中，每个中间值v都基于一个称为“掩码” 的随机数m进行变换，即vmv*m，运算* 通常根据密码算法所使用的操作进行定义，多为布尔异或运算⊕、模加运算+或模乘运算×.在模加和模乘运算的情况下，根据密码算法选择不同的模数.采用多个掩码的秘密共享是一种通用的掩码实现方法，即将多个掩码作用于同一个中间值，采用n个掩码可以抵御n阶DPA 攻击[34].

在布尔掩码中，中间值与掩码进行异或运算，即vmv ⊕m.在算术掩码中，中间值与掩码进行加法或乘法运算，即vmv+mmodn或vmv×mmodn.有些算法会同时基于布尔运算和算术运算，因此需要同时采用两种类型的掩码技术，这将会带来额外的计算开销.

另外，密码算法会使用线性和非线性函数.线性函数可以通过上述掩码技术来解决，而非线性函数一般采用查找表来实现，因此需要构造对应的掩码型查找表Tm:Tm(v ⊕m)T(v)⊕m.这种表的生成非常简单，但是必须穷举所有的掩码m和输入v，然后对应记录的结果.因此随着查找表使用掩码数量的增加，计算所占内存也相应增加.在降低计算开销和提高效率方面，学术界相继提出了一系列的改进方法[35-37].

掩码技术是一种被广泛关注的防御对策，近年来已有大量文章提出了不同类型的掩码方案、安全性证明及相关的元件级应用.

3 基于ADP 的iO 方案

基于ADP 的候选方案是独一无二的，因为它是迄今为止唯一不依赖任何传统密码学假设(如离散对数或LWE) 且未被打破的候选方案.此外，目前的量子技术在破解基于ADP 的iO方面似乎没有显示出特殊优势.因此，如果LWE 在未来被量子算法打破，ADP 的混淆候选方案可能是唯一对抗量子计算机的iO候选方案.该方案通过四个构造来混淆ADP[7]，每一个构造都是在前一个的基础上进行改善，因此本节将按顺序详细介绍Bartusek 等人提出的iO方案[8]，本文后续内容将会在这种iO方案的基础上进行改善及应用.

3.1 随机局部替换

随机局部替换(random local substitutions，RLS) 的目标是通过增加一些顶点和以某种随机的方式修改边来增加BP 的熵，我们用M′(x) 来表示修改后的BP.具体来说就是在每一个顶点对(vi，vj) 上添加一个中间节点vi，j.用M′(x) 的2×2 子矩阵表示该矩阵) 来举例，所在行用vi和vi，j表示，所在列用vi，j和vj表示.

如果顶点vi，vj之间边的标签值为1，那么有4 种随机替换方法:

如果顶点vi，vj之间边的标签值为0，那么有3 种替换方法:

如果顶点vi，vj之间边的标签值为xi，那么有12 种替换方法:

此时ADP 的计算为:

3.2 添加小偶数噪声

首先给出一个结论，对于任意多项式g:Zn →Z 及任意噪声{eiZ}i∈[n]，有

因此，当把ADP 作为输入时，我们可以利用这个结论，向{A，{Bi}i∈[n]}中的每一项添加独立随机偶数作为噪声.然后将加入噪声后的矩阵定义为{A+2E0，Bi+2Ei}i∈[n].评估函数Eval 也需要改变，用Eval/=0代替Evalparity.

此时ADP 的计算为:

3.3 对角矩阵块构造

理想情况下，在混淆ADP 的时候，需要强制对手用预计的方式来计算程序.这个目标可以通过增加矩阵随机性来实现，只有按照固定的方式进行计算才能消除随机性，以其他方式组合矩阵将会使矩阵随机性保持不变，从而隐藏原始ADP 的有效信息.通过采样2n个行列式为1 的随机矩阵{Gi，Hi}i∈[n]，然后将每个Gi沿对角线按矩阵块的方式添加到矩阵A中，同时在Bi中对应的第i个添加Hi-Gi.将处理后的矩阵定义为{diag(A，G1，G2，···，Gn)，{diag(Bi，0，···，0，Hi-Gi，0，···，0)}i∈[n]}.

此时ADP 的计算为:

3.4 矩阵重随机化

重随机化在整个混淆过程中应用了两次，第一次是在加入噪声后，第二次是在构造对角矩阵块后.在这两个步骤中，分别使用均匀的随机矩阵U，V对每个矩阵进行左乘和右乘，来实现ADP 的不可区分性，其中随机矩阵需要满足det(U)·det(V)1.Applebaum 等人[38]给出了详细证明，这里简述一下思路:

假设存在M，M′，其中rank(M)M′r，det(M)det(M′)d.然后对两个矩阵进行矩阵的行变换和列变换，即左右各乘一个矩阵，使得

这就说明集合SQ和的大小是相同的，可以理解为M与M′变成某一个其他矩阵的概率是一样大的，也就是两个矩阵具有不可区分性.

综合上述四个小节，最后ADP 的总计算过程为:

4 侧信道防护方案设计

为了将上述混淆ADP 的候选方案应用于侧信道防护中，本文对上述方案进行了改进.上述方案中使用的ADP 编码过程是对整个程序进行整体ADP 编码，导致生成的ADP 矩阵占用内存过大，而后续使用的混淆方案本身就需要大量的内存消耗，所以对这些矩阵进行混淆时，一旦矩阵规模稍大就会占用数GB甚至几十GB 的内存，这种防护方案的代价太大，无法在真实场景中实施，因此需要对这种方案进行改进.本节利用了抗侧信道的安全性定义弱于传统不可区分混淆的安全性这一特性，对上述方案进行了改进，在实现侧信道安全防护的同时使混淆程序的内存占用大大减小，既能保证安全性又能提高效率，使其能够在真实场景中进行应用.

4.1 总方案设计

ADP 需要满足{0，1}n →{0，1}的映射，本文方案也同样基于这个映射.方案分为两部分: 线性操作和非线性操作.

线性操作就是简单的比特异或操作，将线性映射定义为f，则f(x1，x2，···，xn)x1⊕x2⊕···⊕xn，其中输入xi {0，1}.

而非线性操作是基于查找表的一类ADP 设计，通过查找表画出对应的DAG，然后将DAG 转化成BP，BP 编码成ADP 从而实现非线性操作的ADP 编码，这种做法可以将任意的非线性操作编码为ADP.将非线性映射定义为g，即

其中输入xi {0，1}，°表示非线性操作.而为了抵抗侧信道攻击，我们对这两类操作加入了一阶掩码，能够隐藏真实输入并且更新ADP 矩阵，达到抗泄漏的效果.

原做法[7]中提到的ADP 主要是针对整体的密码算法进行ADP 编码，而ADP 的特性是每多编码一个变量，矩阵的规模就会以O(n2) 的速度增长，这样生成的矩阵占用内存会很大，而经过我们改良后的ADP 可以对这种规模较大的ADP 进行拆分，也就是将整体的密码算法拆解成多个部分的运算再通过掩码方案进行组合，例如对x1⊕x2⊕···⊕xn进行ADP 编码，先进行拆分，对其中的每一个运算xi-1⊕xi(可以是一个运算也可以是n个运算)进行独立的ADP 编码，通过掩码方案产生一个隐蔽后的中间值xm，再进行xm ⊕xi+1的编码，最后将一个大规模的ADP 拆解成n-1 个小规模的ADP 从而降低对ADP进行iO时的运算成本，然后可以分别对这些拆分后的ADP 进行iO构造.

在对ADP 进行混淆构造时，我们采取了第3 节Bartusek 等人[8]提出的候选混淆方案.为了与本文的侧信道防护方案进行结合，对第3 节提出的方案进行了改进.我们保留了3.1 节和3.4 节的构造，去除了3.2 和3.3 节的构造，原因如下:

由于本文方案设计用于侧信道防护方向，而侧信道攻击本身就会产生大量的噪声，这些噪声对矩阵数据的影响比3.2 节添加的小偶数噪声效果更好，因此无需生成大量随机数来模拟噪声，去掉这一构造既能降低随机数的消耗又不会导致安全性的降低.3.3 节对角矩阵块是一种防护密码分析攻击(如多项式拓展攻击) 的构造，这类攻击需要在模拟白盒的条件下进行，即需要知道所有的输入和输出值，而我们的方案设计是针对侧信道攻击进行防护，侧信道防护的安全性定义弱于传统密码分析防护的定义，更远达不到白盒的条件，攻击者并不能通过这个构造的有无获取任何有价值的信息，而且构造对角矩阵块会使得计算成本以O(n2) 的速度提高，是整个方案中内存占用最大的部分，所以去掉这一构造后既不会降低防护的安全性，又能大大降低资源消耗.

综上所述，本文用到的iO方案为:

混淆ADP 方案的整体流程如算法1 所示.

4.2 ADP 更新

上述提及的一阶掩码，放入线性操作中即为

其中输入xi {0，1}，随机数mi {0，1}.想要得出正确结果，只需要将所有随机数异或之后与计算结果进行异或.非线性操作的隐藏过程与之相仿:

其中输入xi {0，1}，随机数mi {0，1}，°表示非线性操作.想恢复正确结果，需要对非线性操作对应的查找表进行分析，然后将所有随机数进行合适的处理后才能恢复正确结果，下一节中将举例说明如何对非线性操作的结果进行恢复.

从函数f，g中可以看出，由于mi是随机生成的，每进行一次计算，mi就会发生一次变化，ADP 也会随之更新，从而达到抗泄漏的效果，保证了ADP 的安全性.ADP 更新算法如算法2 所示.

本文设计的ADP 更新算法可以对ADP 矩阵进行更新，即在每次运行ADP 时生成的ADP 矩阵都不相同，这样被混淆的程序进行ADP 编码后生成的矩阵具有不确定性，从而可以有效防止敌手进行侧信道攻击恢复出原始ADP 矩阵，提高了该侧信道防护方案的安全性.

5 侧信道应用

本节将第4 节提出的侧信道防护方法针对具体的算法进行应用.

5.1 加法应用

将上一节提到的防护方法用于加法中，首先给出一个基于不可区分混淆的ADP 加法器电路结构.加法器由两部分组成: 本位和进位.由于加法器是二进制加法实现，所以本位只需对输入进行异或即可，而进位函数如下:

其中x，y为加法的两个输入值，c为加法的进位值，初始为0，c′为输出结果，c′为输出的进位值，另有随机数mx，my，mc，作为掩码，隐藏输入和输出的值，其中mx，my，mc用于隐藏混淆ADP 加法器的输入值，用于隐藏混淆ADP 加法器的中间输出值且mx ⊕my ⊕mz.通过这个简易的加法器函数可以实现任意比特的加法操作.下面就要针对该函数编码出对应的ADP 并进行混淆.

想要编码ADP 需要对函数进行分析后画出对应的DAG，然后将DAG 分解成BP，对BP 进行编码.函数g(x，y，c) 的运算存在掩码，那对于过程中随机生成的掩码(mx，my，mc) 会编码出不同的ADP.

当(mx，my，mc)(0，0，0) 时，有0，这种情况下掩码并不会影响计算过程和结果(等同于无掩码)，所以输出为1 的情况有4 种:

当(mx，my，mc)(0，1，1) 时，有0，这种情况下输入值被掩码隐藏，如果按照上述情况生成ADP 的话结果显然是不正确的，因为输出为1 的情况有:

而当(mx，my，mc)(0，0，1) 时，有1，这种情况下输入和输出值都被掩码隐藏，其输出结果为1 的情况有:

可以看出，对于不同的掩码组合，相同的输入并不会得到同样的结果，因此针对不同的掩码组合需要编码不同的ADP，这里列出编码ADP 所需的查找表:

因此对于这八种情况只需4 个DAG 即可表示全部情况.以(mx，my，mc)(0，1，1) 为例来介绍编码ADP 及混淆ADP 的全过程.

首先画出(mx，my，mc)(0，1，1) 对应的DAG，如图1 所示:

图1 有向无环实例图Figure 1 Example of directed acyclic graph

然后根据DAG 生成对应的邻接矩阵并对矩阵进行初步处理(处理方法为减去最左一列和最下一行).

再将上述处理后的矩阵分解为仿射函数中的矩阵元组(A，B1，B2，···，Bn).

根据矩阵元组可以计算出ADP 的值:

接着对ADP 进行混淆操作.混淆按照第4 节改进后的iO方案进行操作.第一步按照3.1 节随机局部替换的做法对原始矩阵进行RLS 操作，第二步进行矩阵重随机化操作，随机生成两个矩阵U、V，矩阵需满足det(U)·det(V)1，利用这两个矩阵可以实现det(UMV)det(UM′V) 从而实现矩阵的不可区分.

通过以上步骤实现对ADP 的iO操作从而实现完整的加法应用.

5.2 SHA-2 及BIP-0032 应用

传统非确定性钱包是通过随机数生成多个互不相关的私钥.但是区块链中的用户为了保证自己的安全性往往会生成多个私钥，以保证每次交易不会被追踪，此时非确定性钱包会生成多个公私钥对，这些密钥需要反复备份.

为了解决传统非确定性钱包每当一批私钥用完后必须重新生成一批私钥并且及时备份的问题，分层确定性钱包的定义被提出.分层确定性钱包通过支持从单个根派生出多个密钥对链.BIP-0032 定义了分层确定性钱包，系统会产生一个随机种子，根据种子通过分层确定性推导的方式得到n个私钥，这样保存的时候，只需要保存一个种子就可以，私钥可以推导出来.

BIP-0032 整体流程如下:

首先系统会使用椭圆曲线私钥签名算法SECP256K1 加密算法，利用熵(entropy) 函数产生一个随机的128 比特种子S，然后将S通过HMAC-SHA512 哈希算法产生一组256 比特的父扩展私钥m和一组256 比特的链码c，而m可以通过SECP256K1 生成父扩展公钥M.即

然后就可以使用到子密钥派生(CKD) 函数，通过父扩展私钥求出下一级父私钥，通过父扩展公钥生成下一级父私钥，即

而上述都要用到HMAC-SHA512 哈希算法，算法3 给出SHA512 算法的主压缩循环函数.可以看到算法中除了非线性计算外，还存在7 个64 比特的加法，可以对这些64 比特加法进行混淆从而抵抗侧信道攻击.

6 实验测试与分析

6.1 安全性测试

为了验证本算法的安全性，在ChipWhisperer STM32F4 目标板上进行泄漏评估.使用Picoscope 5244D 示波器，采样率为20.8 MS/s，采集在线计算部分的功耗.首先对功耗曲线进行简单的预处理，即进行滑动窗口平均，以减少噪音数据.

这里采用的滑动窗口平均是简单滑动平均(simple moving average，SMA)，它是取前n个数据点的非加权平均值，而在工程领域，均值通常取自中心值两侧数量相等的数据，这样可以确保平均值的变化与数据的变化保持一致，而不是随着时间的推移而变化.然后参考了测试向量泄露评估(test vector leakage assessment，TVLA) 评估方法，TVLA 将泄漏评估与不断发展的能量分析攻击技术分离开来，将复杂的泄漏检测问题转化为简洁的数理统计步骤，使用固定的统计步骤来捕获能量信息泄漏，且可以通过修改测试向量等方法来捕捉能量信息泄漏，并根据所需的安全要求调整阈值，具有简单高效等优势.

把功耗曲线分为固定输入组和随机输入组，两组曲线间或采集，每组共采集25 000 条曲线.对预处理后的曲线，进行Welch’s t-test 检测[39].在统计学上，Welch’s t-test 是一种双样本位置检验，用于检验两个总体均值相等的假设.Welch’s t-test 是对Student’s t-test 的一种改编，当两个样本的方差和样本大小不相等时，其可靠性更高.当比较的两个样本的统计单位不重叠时，通常会应用这些检验.

将安全阈值设置为4.5，阈值所对应的置信度为99.99%.4 bit 加法运算时的评估结果如图2 所示:

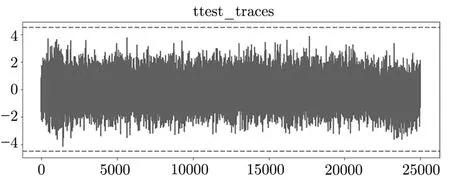
图2 Welch’s t-test 结果Figure 2 Result of Welch’s t-test

可以看出t-test 结果并没有尖端毛刺，均处于红色虚线以内，说明该算法并未产生侧信道泄漏，算法的安全性可以得到验证.

6.2 效率分析

为了测试本算法的效率，对改进后的混淆ADP 方案进行了测试，测试的硬件环境为11th Gen Intel(R) Core(TM) i7-11700 @ 2.50 GHz 处理器.

首先测试利用该防护方案单独实现64 比特加法的速度与在SHA512 上应用该方案的运行速度，测试结果如表1 所示.

表1 防护方案在不同场景下的运行速度Table 1 Operational speed of protection solutions in different scenarios

然后对混淆ADP 占用的内存进行分析，对比分析混淆单ADP 占用内存以及混淆ADP 加法器与编码ADP 变量大小的关系，结果如图3 所示:

图3 ADP 占用内存与变量大小的关系Figure 3 ADP memory usage vs.variable size

通过对比可以看出，采用加法器实现多比特加法所占用内存(增长速度O(n)) 远比直接进行多比特加法编码ADP 占用内存(增长速度O(n2)) 小得多.

最后测试混淆ADP 方案在ARM Cortex M4 处理器上执行的数据，主要测试了不同加法位数在实现时的资源占用，测试说明该方案的计算成本及运行速度都满足实际应用的条件.测试结果如表2 所示.

表2 混淆加法的空间占用Table 2 Memory usage of obfuscated addition

7 结语

本文提出了一种基于不可区分混淆的侧信道防护方案，改进基于ADP 的混淆方法，在保障侧信道安全性的前提下大幅度提高运行效率，从而给出可以执行在嵌入式设备的侧信道防护方法.通过功耗曲线采集对算法进了泄漏评估，并未发现明显泄漏，验证了工作的有效性.对比于传统的侧信道防护方案，该方案将不可区分混淆这一密码学理论与侧信道防护相结合，且抵抗侧信道攻击能力较好.

本方案的研究属于侧信道防护的范畴，而侧信道的攻击与防御技术在不断交替发展，所以进一步的研究可以围绕如何在不降低运行速度的前提下增强算法的安全性以及将iO与侧信道防护深度结合等方面展开.