内容整合突本质 单元促学显素养
王学先 邓印升

《义务教育数学课程标准》(2022年版)明确提出课程内容组织的重点是“对内容进行结构化整合,探索发展学生核心素养的路径”.单元教学设计在促进学生理解和整合知识、建构完善知识体系、发展数学思维能力等方面都有重要作用.学生的数学核心素养是在教学过程中借助教学设计逐渐培养出来的,因此基于核心素养的单元教学设计也应被重视.笔者以“鸡兔同笼”的单元教学設计(章节起始课)为例,阐述在教学中如何提升学生的数学核心素养.
一、教学内容解析
1.内容
本节课选自人教版数学教科书七年级下册第八章.
2.内容解析
本节课内容是以“鸡兔同笼”经典问题为背景,把算术法、一元一次方程、二元一次方程三者进行有机结合,形成系统的单元结构化的教学内容.通过分析问题中的数量关系、让学生脑洞大开,从不同的角度去思考“鸡兔同笼”问题,用逆向思维列出算式去解决问题,通过设未知数,建立方程模型,从正向思维的角度去解决实际问题.建立方程模型是数学常用的一种思想,从实际问题中提取有效信息进行整合,转化为数学问题进行求解,再将数学问题的解进行适当整理来解答实际问题,这是数学上很经典的建模思想,具有很强的应用价值.所以本节课的教学重点:结合实际问题背景构建二元一次方程组,并能正确地解方程组.
二、教学目标解析
1.目标
(1)能够由实际问题列出二元一次方程组,并正确地解答.
(2)会从算术法中对应迁移出解二元一次方程组的不同方法,悟出解二元一次方程组的核心思想是“消元”,从而体会化归的思想.
(3)初步认识用方程解决实际问题的基本架构,体会利用二元一次方程组解决实际问题的优越性.
2.目标解析
达成目标(1)的标志:学生能够从实际问题中提取有效信息,找到已知量和未知量,能正确处理等量关系,并根据等量关系建立方程组,用“消元”的思想来解方程组.
达成目标(2)的标志:学生由“算术法”的启发,得出解二元一次方程组的多种方法,这些方法的核心思想是“消元”,通过转化的方法将二元一次方程组转化为一元一次方程进行求解.
达成目标(3)的标志:学生知晓用二元一次方程组解决实际问题的过程,能在脑海中初步形成本章知识的基本结构,体会用二元一次方程组解决实际问题的优越性,感知数学来源于生活并应用于生活.
三、学情分析
“鸡兔同笼”问题,学生在小学的时候就已经有所接触了.小学主要是通过算术的方法去解决该问题的,且七年级上学期已经学习过一元一次方程,学生已经会用一元一次方程去解决这个问题,而建立二元一次方程组去解决这个问题,是学生之前没有接触过的内容.本节课就是将学生已有的知识经验巧妙地迁移到即将学习的二元一次方程组中去,特别是将算术法中的解题经验迁移到解二元一次方程组中去.所以,本节课的教学难点是通过不同的“算术法”对应迁移出解二元一次方程组的几种方法,并掌握解二元一次方程组的思想是“消元”.
四、教学设计过程
环节1:情境引入,提出问题
《孙子算经》是我国古代一部较为普及的算书,许多问题浅显有趣,其中下卷第31题“雉兔同笼”流传尤为广泛.“雉”是外形像鸡的一种鸟,通称野鸡,“雉兔同笼”后也称“鸡兔同笼”.“鸡兔同笼”是中国古代的数学名题之一.“鸡兔同笼”原题:今有鸡兔同笼,上有三十五头,下有九十四足,问鸡兔各几何?
设计意图:教师以中国经典的“鸡兔同笼”问题引入课题,为“算术法”和二元一次方程组之间的微妙关系埋下伏笔.同时,这样的设计可以提高学生的学习积极性,增强学生的文化自信.
问题1:你能用自己的话说出“上有三十五头”和“下有九十四足”是什么意思吗?
设计意图:教师引导学生进行思考,并分析题目.此问题是本节课的第一个问题,问题设置相对简单,学生不难回答.由浅入深的设问可提升学生回答问题的积极性,从而以高度集中、自信的状态进入课堂.
环节2:善用假设,思考发现
问题2:如何求鸡兔各有几只?你能想到几种算术方法可以来解决这个问题呢?
(1)最帅的方法——“耍兔法”.给这群小动物喊口令:鸡不动,兔子,耍酷!
兔子就全体起立了(兔子两只脚站立)!
兔子起立后脚的总数量:2×35=70(脚)
抬起的兔脚的数量:94-70=24(脚)
兔的数量:24÷2=12(只)
鸡的数量:35-12=23(只)
(2)最神奇的方法——“添脚法”.变变变,把鸡的翅膀变成脚!
脚和鸡翅膀的总数量:35×4=140(只)
鸡翅膀的数量:140-94=46(只)
鸡的数量:46÷2=23(只)
兔的数量:35-23=12(只)
(3)最酷的方法——“金鸡独立法”.让每只鸡都一只脚站立着,每只兔都用两只后脚站立着.
站立后脚的总数量:94÷2=47(只)
兔的数量:47-35=12(只)
鸡的数量:35-12=23(只)
(4)最逗的方法——“吹哨法”.吹一声哨,抬起一只脚,再吹一声哨,又抬起一只脚,这时鸡都一屁股坐地上了,兔子还有两只脚立着.
第一声哨后脚的总数量:94-35=59(只)
第二声哨后脚的总数量:59-35=24(只)
兔的数量:24÷2=12(只)
鸡的数量:35-12=23(只)
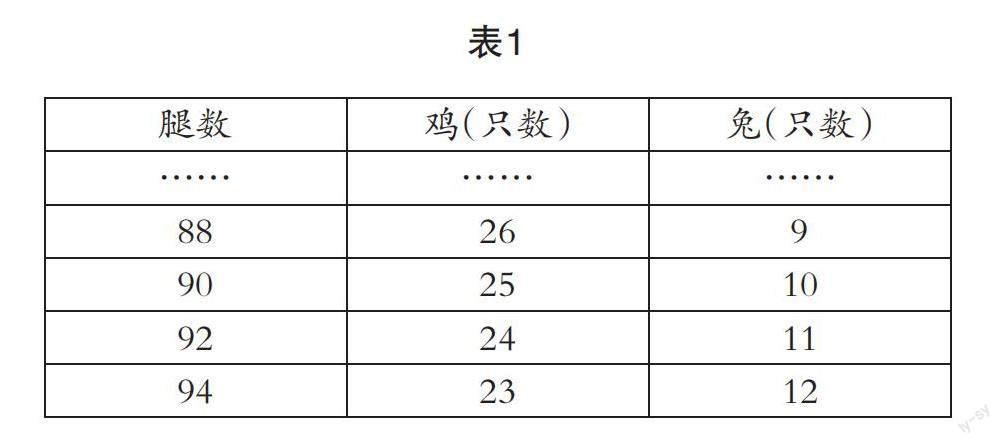
(5)人见人爱的——“列表法”,如表1.
兔的数量:12只;鸡的数量:23只.
设计意图:教师引导学生从不同的角度去思考问题,得到不同的方法去解决问题,激发学生探究问题的兴趣,培养学生的发散性思维.这几种不同的算术方法也为后续用加减消元法解二元一次方程组作铺垫.
环节3:自主探究,数学建模
问题3:如果设鸡有x只,如何解决这个问题?
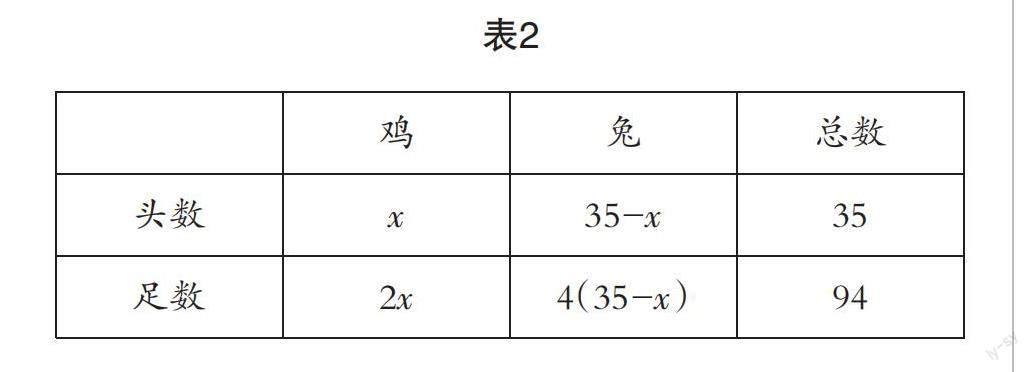
等量关系:鸡头数+兔头数=35,鸡脚数+兔脚数=94.
由表2,得到一元一次方程:2x+4(35-x)=94.
设计意图:学生在用算式解决问题之后,对“鸡兔同笼”问题的数量关系有了一定的理解.教师引导学生运用一元一次方程去解决问题,让学生充分感受算术方法与一元一次方程的异同,也为后面的二元一次方程组进行类比,比较两种方法的优劣.
问题4:如果设兔有x只,怎样解答这个问题?
设计意图:教师从一元一次方程的角度,另设未知数,得到另一种新的方法解决问题,发散学生的思维.
问题5:如果设鸡有x只,兔有y只,怎样列出二元一次方程组?
等量关系:鸡头数+兔头数=35,鸡脚数+兔脚数=94.
设计意图:由一元一次方程自然过渡到本节课的新知,教师引导学生设两个未知数,建立新的方程模型,从二元一次方程组的角度去分析问题、解决问题,引出本节课的新知——二元一次方程组.
问题6:怎样解这个二元一次方程组?
由①得x=35-y③,
把③代入②得2(35-y)+4y=94,y=12.
把y=12代入③得x=23.
答:鸡有23只,兔有12只.
设计意图:教师在解方程组的过程中运用了代入消元法,让学生感知解决二元一次方程组的思想是“消元”——消去其中一个未知数,将“二元”转化成“一元”进行求解.
环节四:思考问题,整合知识
问题7:根据“耍兔法”,怎样解这个二元一次方程组呢?
由①×2得2x+2y=70③.
②-③得(2x+4y)-(2x+2y)=94-70,
化简得2y=24,即y=12.
把y=12代入①得x=23.
答:鸡有23只,兔有12只.
设计意图:受“耍兔法”的启发,教师引导学生将该算术方法的思想迁移到解二元一次方程组中——扩大①式未知数x的系数,使得两式中未知数x的系数相同,两式相减消去x,將“二元”转化成“一元”进行求解.
问题8:根据“添脚法”,怎样解这个二元一次方程组呢?
由①×4得4x+4y=140③.
③-②得(4x+4y)-(2x+4y)=140-94,
化简得2x=46,x=23.
把x=23代入①得y=12.
答:鸡有23只,兔有12只.
设计意图:受“添脚法”的启发,教师引导学生将该算术方法的思想迁移到解二元一次方程组中——扩大①式未知数y的系数,使得两式中未知数y的系数相同,两式相减消去y,同样也可以将“二元”转化成“一元”进行求解.
问题9:根据“金鸡独立法”,怎样解这个二元一次方程组呢?
由②÷2得x+2y=47③.
③-①得(x+2y)-(x+y)=47-35,
化简得y=12.
把y=12代入①得x=23.
答:鸡有23只,兔有12只.
设计意图:受“金鸡独立法”的启发,教师引导学生将该算术方法的思想迁移到解二元一次方程组中——利用等式的性质缩小②式中未知数x的系数,使得两式中未知数x的系数相同,两式相减消去x,同样也可以达到“消元”的目的.
问题10:根据“吹哨法”,怎样解这个二元一次方程组呢?
由②-①得x+3y=59③
③-①得(x+3y)-(x+y)=59-35,
化简得y=12,
把y=12代入①得x=23.
答:鸡有23只,兔有12只.
设计意图:受“吹哨法”的启发,教师引导学生将该算术方法的思想迁移到解二元一次方程组中,两次相减也可达到消元的目的来解二元一次方程组.
环节五:理解方法,内化知识
①算术法:计算简单,分析有难度.
②一元一次方程:容易理解,计算相对简单.
③二元一次方程组:比一元一次方程还容易理解,能更清晰、直接地表示等量关系.
设计意图:通过师生共同探究,教师让学生比较三类解决“鸡兔同笼”问题方法的优点和缺点,让学生进一步体会这三种方法各自的特点.
环节六:学以致用,巩固新知
练习1:有若干只鸡和兔子,它们共有88个头,244只脚,鸡和兔各有多少只?
练习2:1个停车场一共停了15辆车,有三轮车和轿车,共有52个轮子,求三轮车和轿车各有多少辆?
提示:(1)算术法可以用“添轮法”“减轮法”或“独轮法”等;(2)方程建模,万能解题.
设计意图:通过不同类型的练习,教师带领学生巩固本节课的内容和基本思想,抓住该类问题的本质特征来解决实际问题.
环节七:课堂小结,分享收获
(1)从知识点的角度谈谈你有哪些收获?
(2)从数学思想的角度谈谈你有哪些收获?
设计意图:教师让学生从不同的角度谈本节课学习的主要内容,引发学生更深层次的思考,增强学生对实际问题的应用意识,促进学生数学思维品质的提高,形成系统的单元结构化的知识框架.
五、基于单元教学设计提升学生数学核心素养的几点思考
1.确定核心素养导向的教学目标
核心素养导向的教学目标对教学过程有着很强的指导作用,整个教学内容应围绕教学目标来进行设计,所以确定核心素养导向的教学目标就显得尤为重要.确定核心素养导向的教学目标时,教师应确保对每一个单元课时内容的关联及层次性有更清晰的认识,要站在整体知识结构化的视角上来考虑数学核心素养在教学中的达成来制定符合学生学情的单元整体目标,再依据单元整体目标制定具体的课时目标,并且确保制定出来的教学目标是结构化的、能操作的、可评价的.教师应围绕教学目标和学生核心素养的落实来精心设计教学,加强学生知识的连续性和结构化,从而提高课堂效率.
2.將教学内容进行有效整合
单元教学设计既要关注知识的整体性,又要关注不同部分的关联性;本节课以解决实际问题为主线,将算术法、一元一次方程与二元一次方程组进行有机结合,同时将四种算术方法分别巧妙地迁移到二元一次方程组的解法上去,用不同的方法均可达到“消元”的目的,从而将二元一次方程组转化成一元一次方程来进行求解.这样的教学设计将本章的知识进行合理整合,形成了系统的知识结构,避免了将碎片化的知识呈现给学生,让学生形成对本章内容相对整体的认知结构.
3.用“问题驱动”的方式推动教学
用问题串的形式来进行教学是常用的一种教学方式,能引起学生的注意和思考,可以充分发挥学生的主动性,所以教师要在问题的设置上下功夫.问题设置要围绕本节课的教学目标和想要落实的核心素养循序渐进地进行.同时,问题串的设置还应该简洁明了,指向性要强,由浅入深,达到让学生深度学习和深度参与的教学目的.本节课用了10个设问,将学生已有的知识经验与新课内容紧密结合,用层层递进的方式,驱动学生去分析问题和解决问题,引导学生对知识点进行分析、归纳,感受数学思想方法,从而培养学生解决问题的能力.
4.始终“以学生为中心”设计教学
学生始终是学习的主人,教师在进行教学设计时要围绕学生进行合理设计,要能充分发挥学生学习的积极性和主动性;根据教学内容联系实际生活,巧妙设计教学情境,营造一种相对融洽的教学氛围引起学生的情感共鸣,提升学生学习数学的信心,激发学生的学习兴趣.同时,教师应采用多种教学方式,让每一个学生都能深度参与到课堂中去,从“学会”到“会学”,教会学生用数学的眼光去观察现实世界,用数学的思维去思考现实世界,用数学的语言去表达现实世界.
学生数学核心素养的提升需要教师用心设计好每一节课,让数学核心素养在课堂上润物细无声地落地.
◇责任编辑 邱 艳◇

