一种具有机动目标加速度补偿的制导律设计
王重阳,王敏,李慧,许振领,苏振强
(中国人民解放军63892 部队,河南 洛阳 471003)
现代战争中,巡航导弹、反舰导弹等精确制导武器的大量应用使地面与海面目标所受到的威胁日益严重。目前主要通过防空导弹对巡航导弹、反舰导弹进行有效拦截,而采取大机动突防是巡航导弹、反舰导弹突破防空导弹防御区的有效手段。防空导弹普遍采用比例导引等传统的制导律,其制导指令在拦截点附近都存在过载指令较大的现象,特别是拦截大机动目标,比例导引往往存在滞后性,在即将拦截的时刻需用过载指令大而造成脱靶量较大。
文献[1-11]主要采用微分几何、最优控制、滑模变结构控制等控制理论针对机动目标进行制导律设计,与比例导引相比面对机动目标制导效果有了较好的改善,但用到控制理论较深,制导律形式较为复杂。文献[12-18]这些经典的末制导律设计思想主要采用各种滤波算法对机动目标的加速度进行估计,根据估计的目标机动加速度对制导律进行补偿,但其滤波算法计算过程较为复杂。
采用经典的PID 控制方法推导出对固定目标与机动目标的零化视线角速率制导律[19-20],并采用经典的扩展卡尔曼滤波方法估计出机动目标的机动加速度,对所设计的制导律进行目标机动加速度补偿。并通过计算机仿真验证了目标机动加速度的估计精度,提高了拦截机动目标的制导性能。
1 具有目标机动加速度补偿的末制导律设计
经典的PID 控制器最主要的优点是根据目标状态与实际状态之间的误差去实时消除这个误差,而并不是依靠输入与输出之间的关系。所以,这也是经典的PID 控制器被广泛采用的主要原因。
基于经典PID 控制器的误差反馈控制思想可以设计零化视线角速率的制导律。首先,针对固定目标设计,如图1 所示,以纵向平面为例,建立导弹打击固定目标的相对运动方程。
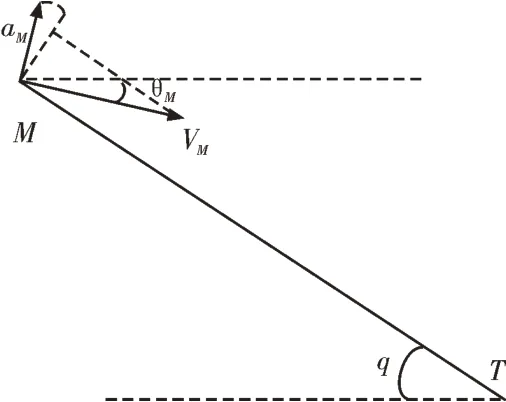
图1 导弹打击固定目标弹目相对运动关系
对式(1)弹目相对运动方程中第二式求导并化简可得:
从而,设输入量u=-aMq,输出量y=,得出系统的传递函数即为被控对象的传递函数,如式(4)所示:
零化视线角速率控制思想是在拦截目标时刻弹目视线角速率为零,设定目标初速值v0=0,利用误差反馈控制的方法,设定的目标值与系统实际状态之间的误差e=v0-y,根据该误差来决定控制力u,系统在该控制力的作用下,最终输出达到设定值v0=0。反馈控制过程如图2 所示。

图2 经典误差反馈控制
系统闭环传递函数为:
由y=,u=-aMq,v0=0,可得:
式(7)表明,拦截固定目标的零化视线角速率制导律就是比例导引制导律。
同理,对于大机动目标,也可以采用基于经典的PID 控制器误差反馈控制的思想,设计零化视线角速率的制导律。以纵向平面为例,如图3 所示,建立导弹拦截大机动目标的相对运动方程。
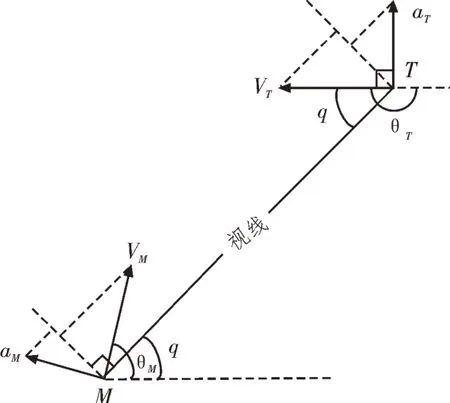
图3 导弹拦截机动目标弹目相对运动关系
对式(8)弹目相对运动方程中第二式求导,并按照前面理论将导弹轴向加速度与侧向加速度和目标轴向加速度与侧向加速度都投影到垂直与弹目视线方向,化简可得:
式(9)与式(3)相比多了目标垂直于弹目视线上的加速度,根据针对固定目标的零化视线角速率制导律的设计方法,设输入量u=aTq-aMq,输出量y=设定期望值v0=0,可以将输入控制量表示为u=ke=k(v0-y),与式(6)相同。从而,拦截大机动目标的零化视线角速率制导律为:
由于大机动目标在末段巡航速度VT变化不大,所以目标垂直于视线方向上的加速度可简化为aTq=aTcos(θT-q),所示式(10)可写为:
从式(11)可以看到,目标侧向加速度aT为导引头无法提供的信息量,所以需要准确估计aT,如果可以将aT估计得较为准确,该制导律拦截大机动目标就相当于比例导引制导律拦截固定目标。
2 目标机动加速度估计
机动目标跟踪的最基本问题是建立机动目标模型。而建立机动目标模型一般既需要满足实际机动情况又要便于数学计算处理。近些年来,许多学者根据机动模型不同特点,采用不同的方法建立了多种机动目标的数学模型。其中常见的有:常速与常加速模型、时间相关模型、半马尔科夫模型、“当前”统计模型等。
“当前”统计模型的主要思想:当目标正以某一加速度进行机动时,下一时刻的加速度取值是有限的,且只能在“当前”加速度的邻域内。由于“当前”统计模型对机动目标加速描述更为准确并且模型描述也不复杂,因此对目标机动加速度信息的估计采用“当前”统计模型[6]。当目标“当前”加速度为正时,概率密度函数为:
由瑞利分布的统计特性可知,只需得到参数μ就可以确定其分布特性,从而得出机动目标加速度方差为:
纵向平面的设计与航向平面的设计过程相同,故以一个平面为例展开设计,建立导弹拦截目标的系统模型:
建立导引头观测模型:
设状态变量为X=[R,q,θT,αT,θM]Τ,导引头观测值为Y=,将系统模型改写为状态空间描述的形式,如下:
为了便于计算机处理,要将系统方程与观测方程进行离散化,首先将X(t)与Y(t)进行泰勒展开,假定卡尔曼滤波的一次计算周期时间为Δt,令t=k,t+Δt=k+1 代入式(16)并整理即可得到离散化后的系统状态方程。
扩展卡尔曼滤波(Extended Kalman Filtering,EKF)是将非线性函数φ(·)围绕标称状态滤波值(k/k)进行泰勒展开,并略去二次及以上高阶项后得到非线性系统的线性化模型。
利用扩展卡尔曼滤波对离散化后的系统状态方程进行线性化得到式(17)。
有了离散化与线性化后的系统方程,就可以采用卡尔曼滤波对目标机动加速度aT进行估计。
其中,式(18)第四步估计的状态向量X(k+1/k+1)的第四个分量即为目标机动加速度aT。通过计算机程序即可解算出目标机动加速度aT用于具有机动目标加速度估计的制导律式(11)中。
3 计算机仿真分析
以防空导弹拦截机动目标为例验证该制导律的性能。防空导弹末制导初始速度800 m/s,末制导初始时刻位置坐标(0,100,0)。目标为速度300 m/s 的亚音速空面导弹,初始位置坐标为(8 000,500,900),目标机动方式为空间螺旋机动,机动角频率为0.5π rad/s,仿真步长10 ms。
采用比例导引制导律对机动目标进行拦截,仿真结果如图4、图5 所示。
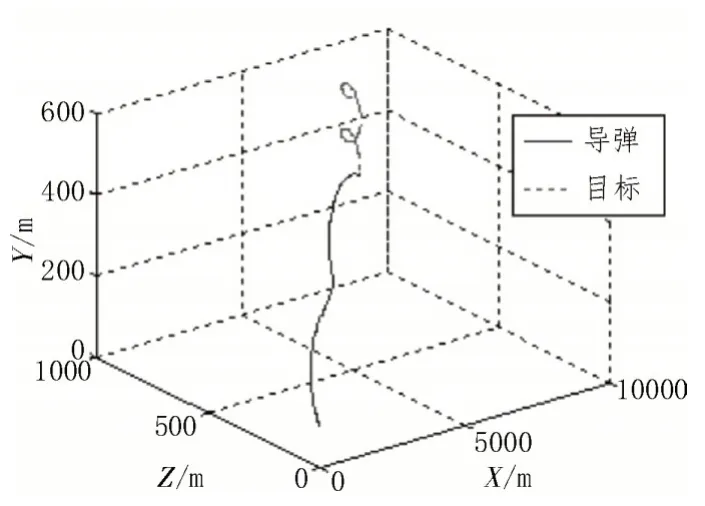
图4 比例导引三维弹道
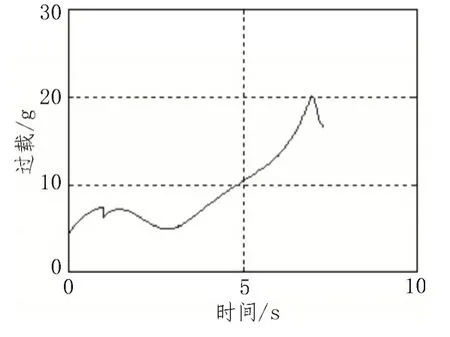
图5 比例导引下导弹的复合过载
采用具有目标机动加速度补偿的制导律对机动目标进行拦截,仿真结果如图6-9 所示。
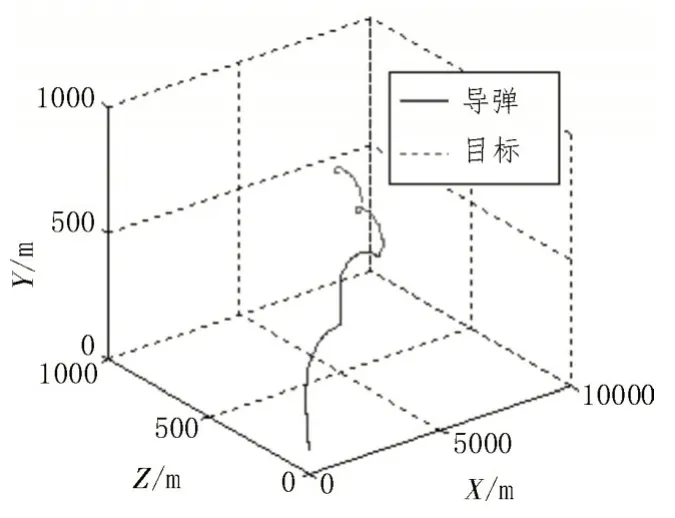
图6 设计的制导律的三维弹道
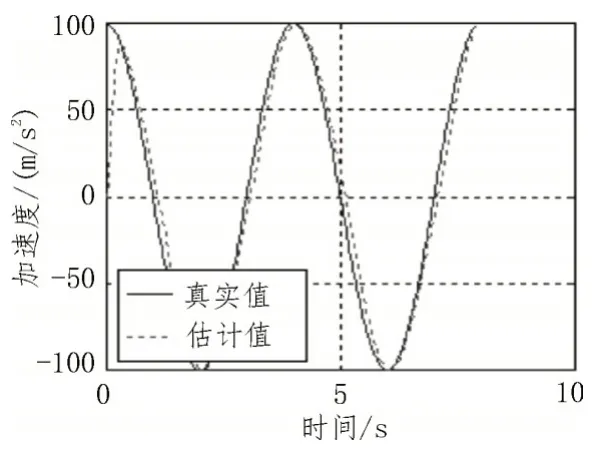
图7 铅垂方向目标加速度估计
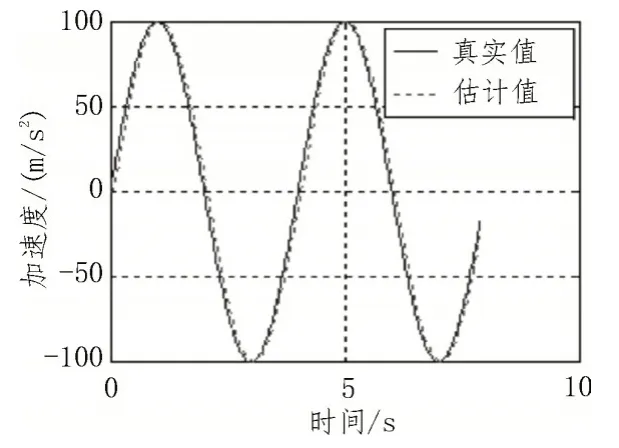
图8 水平方向目标加速度估计
在仿真过程中,比例导引的制导方式仿真时间为7.52 s,脱靶量为8.41 m;具有目标机动加速度补偿的制导律仿真时间为7.74 s,脱靶量为1.72 m。
对比图5 与图9 结果表明,采用比例导引制导律防空导弹拦截末段过载接近20 g,而采用具有目标机动加速度补偿的制导律前段过载大末端过载收敛到11 g,这样给导弹末段留有较大的机动能力,从而致使脱靶量要小于比例导引。
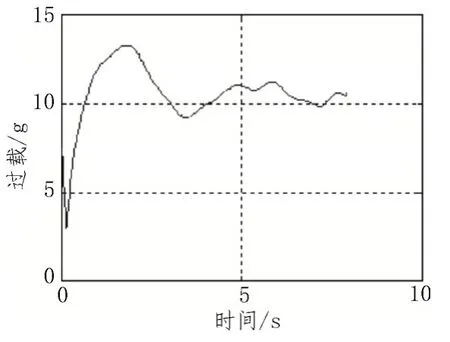
图9 采用所设计制导律情况下导弹的复合过载
由图7 与图8 结果表明,采用扩展卡尔曼滤波的方法对目标机动加速度的估计最大误差为6%,估计精度较高。验证了具有目标机动加速度补偿的制导律对大机动目标的有效性。
4 结论
基于反馈控制的思想设计了可拦截大机动目标末制导律,设计采用经典PID 控制中误差反馈的方法推导出了结构简单实用的拦截大机动目标末制导律。这种制导律需要已知目标机动加速度,通过建立机动目标的“当前”统计模型与弹目相对运动方程,并且对模型进行离散化、线性化,利用扩展卡尔曼滤波的方法估计出目标机动加速度信息。在目标机动加速估计精确度较高的情况下,这种具有目标机动信息补偿的末制导律对大机动目标的拦截相当于比例导引制导律对固定目标拦截。通过计算机仿真证明,该制导律能比较有效解决拦截大机动目标脱靶量较大的问题。

