交流电机驱动弹性连杆式振动机械的Sommerfeld 效应分析

陈晓哲，刘俊岐，钟 山，李凌轩

（东北大学秦皇岛分校控制工程学院，河北 秦皇岛 066004）

引言

在人类生产活动中所应用的机械设备都是由各式各样的内燃机和电动机等原动机来提供动力输出的。受能量守恒限制，所有的原动机能够提供的动力都是有限的，统称这类提供有限动力的原动机为非理想原动机［1］。在一般机械系统研究中，因电机部分与机械部分无运动耦合关系，往往不考虑机械部分的运动对原动机的影响。但是在振动系统中，由于系统振动运动的变化速度与原动机转速同频，系统的振动运动会显著影响原动机的旋转运动，进而形成一种机电耦合作用［2］。特别是在近共振区工作的振动机械，由于系统运动振幅较大，需要输入更多的外部能量，这就会造成原动机的动力不足，最终导致原动机无法升高转速。当继续增加能量输入时，就会出现原电机转速的跳跃现象，即从共振前直接跳到共振后，这种非线性跳跃现象被称为Sommerfeld 效应，此类系统也被称为非理想振动系统［1-2］。因此，在非理想振动系统的研究过程中，需要考虑Sommerfeld 效应。

国外学者在不同机构中对Sommerfeld 效应展开了一定的研究，但是采用的原动机多为直流电机模型。针对单盘转子系统，Bharti 等［3］研究了转子二阶共振处的Sommerfeld 效应。对于转子系统中存在Sommerfeld 效应而导致转速不能升高的问题，Jha 等［4］利用主动磁轴承来衰减系统内阻尼进而控制Sommerfeld 效应的发生。在悬臂梁系统中，Jiang等［5］采用模态法对梁进行离散，研究了弹性质体的Sommerfeld 效应。在曲柄滑块模型中，Sinha 等［6］对往复机构产生的Sommerfeld 效应进行了分析。显然一个非理想源可以产生跳跃现象，两个非理想源有可能会产生自同步现象。基于单质体模型，Kovriguine 等［7］对比了一个偏心转子和两个偏心转子的Sommerfeld 效应。Djanan 等［8］采用两台直流偏心电机对弹性矩形板系统的Sommerfeld 效应进行了研究，采用偏心转子自同步的方式减小了弹性板的振动。针对两个偏心转子系统，Zhang 等［9］研究了一类双质体振动系统中的转子自同步和Sommerfeld 效应。在动力吸振器模型中，Felix 等［10］基于Sommerfeld 效应研究了能量回收。考虑弹簧非线性，González-Carbajal 等［11］研究了电机机械特性曲线的斜率对Sommerfeld 现象的影响，并且发现了非线性系统中存在霍普分岔。目前，国内学者对Sommerfeld 效应研究较少。孔祥希等［12］对一个质量偏心单盘转子系统的Sommerfeld 效应及不平衡响应进行了分析。姜娇等［13］考虑一个偏心转子作激励源的单质体振动系统，应用线性系统的解研究了该机构的Sommerfeld 效应。

考虑到弹簧连杆式振动机械在各工业部门应用比较广泛，并且其采用交流电机作为原动机，有必要对该类型的振动机械进行Sommerfeld 效应的研究。在上述研究基础上，本文引入交流电机的数学模型，建立该类振动系统的动力学模型，通过理论分析和数值仿真为该类振动系统的设计提供理论依据。

1 机电耦合动力学模型

如图1 所示，为一类交流电机驱动的连杆式振动机械。交流电机驱动偏心机构使弹性连杆往复运动，弹性连杆上的传动弹簧（刚度为k1）使振动台产生振动。振动台（质量为m）与底座之间采用主振弹簧（刚度为k0）连接。由于有导向杆的限制作用，振动台只能在垂直于导向杆x方向上运动。其中，r为偏心半径，φ为偏心轴转角，c为主振弹簧阻尼系数。

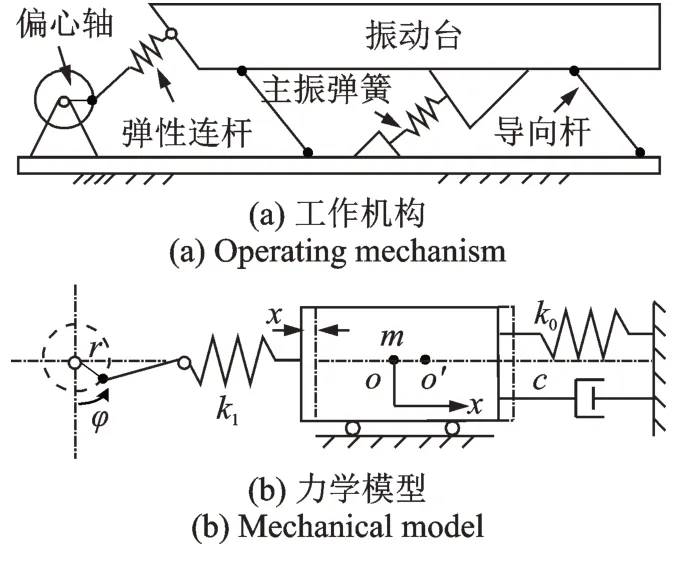
图1 弹性连杆式振动机械Fig.1 The elastic connecting rod vibration machine

综合考虑振动系统的机电耦合作用，引入交流电机数学模型［14］，基于拉格朗日方程建立机电耦合系统的动力学数学模型为：

其中，ωs=2πf为定子角频率，ω为转子角频率；k=k0+k1，“•”表示d(•)/dt，“••”表示=d2(•)/dt2，Te为电机电磁力矩，其他电机参数详见表1。

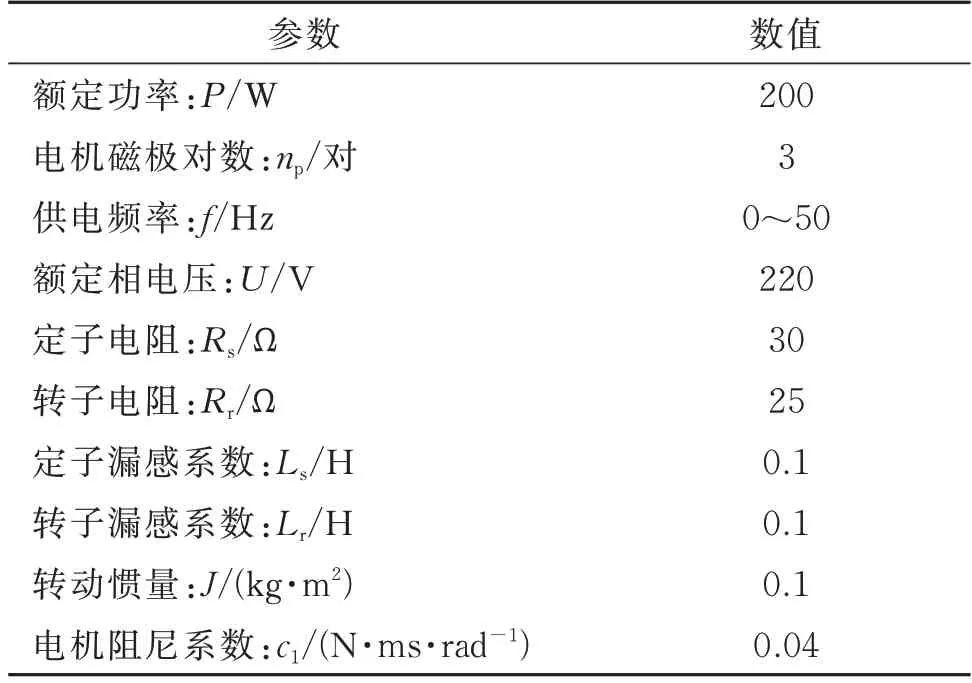
表1 电机参数表Tab.1 Parameters of motor

2 理论分析

2.1 理论推导

对比电机运动方程［14］，可知式（2）中等号右端第二项为负载力矩，其中k1rxcosφ为机电耦合项。根据非理想源特性［1］，需要研究x为最大时，是否会使原动机无法提供足够的动力。众所周知，只有当系统运动处于共振区时，系统响应x接近最大。因此，接下来将研究系统共振时的情况。

系统运动在共振区时，阻尼项和外部激励项均可以认为是小项［15］。通过引入小参数ε，将式（1）进行无量纲化，得：

如果系统处于稳态运动，即ε=0 时，系统的振幅A和相角Θ应为常数，可以设式（3）的解为：

如果ε≠0 时，A和Θ都将随着时间t缓慢变化，此时系统频率为=Ω，因此应为：

所以，x对时间t的二次导数可化简为：

将式（4）和（7）代入式（3），得：

式中εχ2=k1r/J，εσ1=ωn-Ω。

根据dφ=Ωdt，对上述方程组进行换元表达：

式中εTm(Ω)=[Te(Ω)-c1Ω)]/J；•'=d(•)/dφ。

虽然Ω，A和Θ是t或φ的函数，但是它们是随时间缓变的，仍可以看作平均变化量与小的振动变化量叠加而成，所以可以设成如下形式［15］：

式中fΩ，fa和fθ为小的振动项。

因此，可取在周期2π 内Ω，A和Θ的平均值来作平均变化量部分：

式中εσ2=ωn-ω。

整理式（16）～（18），可得一次近似解：

当振动系统处于稳态运动时，响应的状态量应为常量，可以得到如下条件［15］：

将式（22）代入式（12）～（14），得：

联立式（24）和（25），可得振动系统一次近似的振幅和相角：

将式（26）和（27）代入式（23），得系统稳态运动时，电机的运动方程：

式中TL(ω)=c1ω+cωna2/2 为电机总负载力矩。

值得注意的是式（28）是关于角速度ω的超越方程，本文在第3 节的讨论中采用了数值方法。

2.2 稳定性分析

接下来研究振动系统运动的稳定性。将式（12），（13）和（14）表达成如下形式：

根据一次近似稳定性判别法，求式（29）的Jacobi 矩阵［15］，得：

式（30）的特征方程为：

根据Routh-Hurwitz 定理，得到振动系统稳定性条件：

根据式（32），可得第一稳定性条件：

从式（33）中可以看出，由于实际机械系统参数均为正值，所以第一项和第三项必为正值。如果满足dTe(ω)/dω<0，第一稳定性条件就必然得到满足。显然，根据交流电机机械特性曲线［1］，此条件很容易得到满足。

根据式（32），可得第二稳定性条件：

由于式（34）中括号内项均为平方项，因此可以得到进一步简化后的第二稳定性条件：

根据式（32），可得第三稳定性条件：

观察式（36）可知，除中括号项外，其余项均为正值。如果满足Tn=d(Te-c1ω)/dω<0，只须要求ωn>ω，第三稳定性条件也一定满足。

3 数值分析

本节将通过数值法对所研究的对象进行定量的分析，其中振动参数为m=20 kg，k=30 kN/m，c=54.22 N·s/m，r=0.1 m，k1=1 kN/m，其余相关电机参数如表1 所示。

图2 为不同供电频率下，电磁力矩Te与负载力矩TL随电机转速的变化曲线。从图中可以看出，交流电机的机械特性曲线具有非线性特征，Te随着电机输出角速度ω先升后降，这点是不同于直流电机的。两种力矩的交点代表着可以满足式（28）的平衡状态，即可以保证系统实现稳态运动。同时也能看出交点都处于Te的下降区，这正好符合第一稳定性条件要求的dTe(ω)/dω<0。由于TL曲线在共振区会出现非线性变化，即出现波峰状态。这就会导致两种力矩曲线在共振区内可能存在三个交点。图中五条曲线，21 Hz 和26.3 Hz 的Te与TL只有一个交点，这说明并非所有频率都存在Sommerfeld 效应，该现象在共振区工作的频率有可能出现。22.3 Hz 和25 Hz 的两条曲线给出该电机参数可能会存在该现象的频率界线。根据第三稳定性条件，两种力矩的交点在共振前，即ω<ωn，就是稳定的点。

图2 角速度-力矩Fig.2 Angular velocity-torque

为了更一步分析Sommerfeld 效应的产生机理，将两种力矩做差后绘图，如图3 所示。根据能量守恒，当Te=TL时，系统达到稳态。因此，曲线的0 点所对应的角速度就是系统最终稳态对应的角速度。值得注意的是，23.6 Hz 曲线存在三处等于0 的点。根据第二稳定性条件，两种力矩差的导数应为负值才能保证点是稳态点。23.6 Hz 曲线中间0 点处的导数为正值，所以该点是不稳定的点。

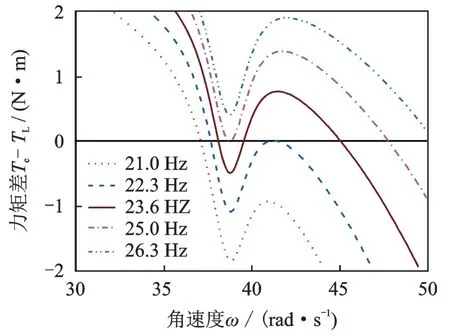
图3 角速度-力矩差Fig.3 Angular velocity-torque difference

通过上述分析解释了Sommerfeld 效应的产生机理，接下来将针对Sommerfeld 效应对系统稳态运动的影响进行讨论。

图4 给出了系统的一次近似振幅a和角速度ω在不同供电频率f下的变化规律。在图4（a）中，a的曲线在共振区出现了波峰，但是不同于线性系统，a的曲线出现了硬式非线性特征。随着f的增加，a由p1点跳到p2点；随着f的减小，a由q1点跳到q2点。上述现象产生的原因可见图4（b）所示，ω随f的增大而升高，但是在共振区却出现非线性变化，即频率俘获。从能量守恒的角度来分析，系统共振时需要更多的能量来维持运动，这就增加了电机的总负载力矩。电机在升速过程中得到的外部能量几乎全部用于维持系统共振运动。因此，电机输出的角速度即使增加，供电频率也不会提升，出现了一种角速度被俘获的现象。当电机获得足够的能量后，可以克服共振时负载力矩需要的能量，根据电机运动方程，电机的角速度得到了增加。由于角速度产生了变化，系统外部激振频率也相应跟着变化，并且远离了共振点。这样就会导致系统不再需要这么多的能量来维持共振运动，而已经获得的这部分能量由共振运动再次传递回电机的升速运动。最后，大量的能量全部用于角速度的提升，就会造成其曲线产生跳跃现象。同理当减小供电频率，系统的共振运动出现滞后现象，即经过升频的跳跃点时，也没有产生共振。当再次降低到一定频率时，由于系统产生共振运动，瞬间需要较大的能量。因此，原先用于维持电机旋转运动的能量再次被转移至共振运动，就会造成电机转速的突然下降。上述分析从能量转换的角度再次解释了Sommerfeld 效应。图4（c）为第二稳定性条件，从图中可以看出只有p1～q1段是大于0的，因此该段内的所有运动均是不稳定的。接下来为验证理论解的正确性，对式（1）和式（2）进行数值仿真。

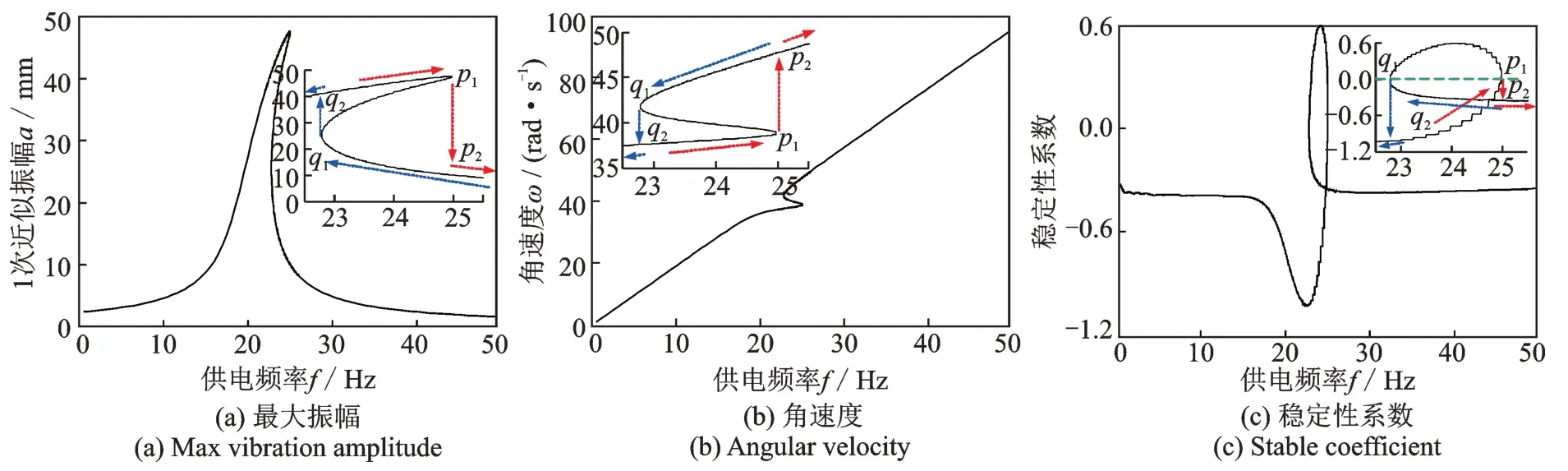
图4 供电频率-不同参数Fig.4 Power frequency-different parameters

图5 选用23 Hz 作为电机的供电频率进行数值仿真。考虑到22.3 Hz 和25 Hz 为频率界线，为了方便对比，本例选用3 Hz作为调节频率步长。如图5（a）所示，电机在增频过程中，因23 Hz<25 Hz，仍处于共振前阶段，对应角速度约为38 rad/s。当增频至26 Hz，大于共振点，角速度产生很大的跳变，约为45 rad/s。为了验证硬式非线性特征，将频率下调回23 Hz，而角速度却下降得很少，约为44 rad/s。这说明了相同供电频率下，系统存在两个稳定工作点，共振点前后各存在一个，这个现象也可以从图5（b）中发现。最后，再次将频率下降至20 Hz。由于离开了Sommerfeld效应区间，角速度跃至约37.5 rad/s，再次回到共振点前。本例展示了角速度的跳跃、系统频率俘获和系统响应的迟滞共振等现象，同时也验证了本文所采用的解析方法的有效性和准确性。

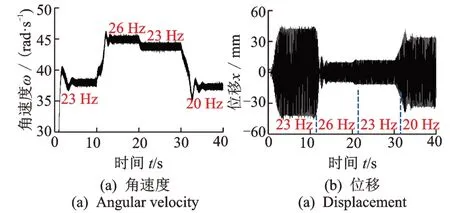
图5 时域响应Fig.5 Time domain response

通过前面关于Sommerfeld 效应的研究可知，角速度跳变的最终状态是由电机提供的能量在转子旋转运动和系统振动运动之间互相传递来决定的。下面，将结合不同的振动参数对Sommerfeld 效应进行定量的研究，从而给相关机械系统参数设计提供理论支持。如图6 所示，图6（a）为不同参振质量m下，电机负载力矩TL的变化情况。从图中可以看出，随着参振质量增大，TL的波峰逐渐左移，并且波峰变窄。这些变化均是由于固有频率变小导致的。但值得注意的是，仅改变参振质量对避免发生Sommerfeld效应影响规律不一。虽然m=30 kg 处于中间位置，可是不存在Sommerfeld 效应。图6（b）为不同主振刚度k条件下，电机负载力矩TL的变化情况。因为改变主振刚度也会导致系统固有频率的变化，进而可以避免Sommerfeld 效应的发生。因此，选择工作在近共振区的机构，需要慎重选择电机型号，从而避免主振刚度变化引起Sommerfeld 效应发生。图6（c）为不同偏心半径r条件下，电机负载力矩TL的变化情况。因为偏心半径影响激振力，从而影响系统振幅的峰值，从图中可以看出，适当减小r的数值，可以避免Sommerfeld 效应的发生。图6（d）为不同传动刚度k1条件下，电机负载力矩TL的变化情况。同r变化一致，k1也影响着激振力。但是过小的k1会影响激振力的传递。图6（e）为不同电机阻尼系数c1条件下，电机负载力矩TL的变化情况。电机阻尼系数本质上不同于其他振动参数。该系数过大会影响系统的有效功率，应尽可能地减小。从图中也可以看到，如果减小该参数后，也会避免Sommerfeld 效应的发生。

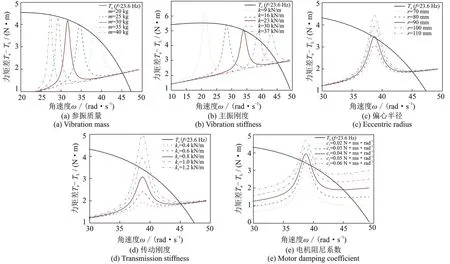
图6 不同参数情况下负载力矩曲线Fig.6 The load torque curves with different parameters

4 结论

本文以一类弹性连杆式振动机械为研究对象，考虑其为非理想振动系统，引入交流电机模型，建立了该系统的机电耦合动力学模型，通过解析和数值仿真两种方法定量地研究了该振动系统的Sommerfeld 效应。相关结论如下：

（1）验证了交流电机驱动的弹性连杆式振动机械也存在Sommerfeld 现象，即电机转速呈现跳跃式突变现象，并且振动系统的幅频特性曲线也呈现出硬式非线性特征。

（2）证明了Sommerfeld 效应的本质是由于稳态电机运动方程的多根特征导致的。由于该方程是超越方程，当接近共振区时，方程会存在三个解，其中一个解对应着不稳定状态。

（3）针对关键性系统参数进行了定量分析发现，参振质量对Sommerfeld 效应影响规律不统一；偏心半径、传动刚度及电机阻尼对Sommerfeld 效应影响较大，且变化特征基本一致；而系统刚度因其变化影响系统固有频率，所以对Sommerfeld 效应影响最大。