MEMS三轴加速度计误差标定与补偿方法研究

刘有彬，闫 欢，彭根斋，白 雪，杨 勤

（中国电子科技集团公司第九研究所，四川 绵阳 621000）

0 引 言

微机电系统（MEMS）三轴加速度计［1］是电子罗盘倾斜角测量与补偿的核心器件，其测量精度直接影响电子罗盘的整体性能［2］。在实际应用中，MEMS 三轴加速度计存在较大的测量噪声，甚至可达数百mgn，必须对输出的原始数据进行滤波，尽可能减小测量噪声；另外，MEMS 三轴加速度计受自身制造误差和安装误差的影响，也会产生较大的加速度测量误差，严重影响电子罗盘的倾斜角测量与补偿精度。因此，使用前必须对MEMS 三轴加速度计的相关误差进行标定与补偿，提高其测量精度。因材料、设计、工艺等原因，MEMS三轴加速度计每个轴的参数并不一致，从而表现出不一致的零偏、刻度因子、正交性误差。另外，安装过程中还会引入安装误差，由于正交性误差和安装误差的引入，MEMS三轴加速度计的标定方法相较于单轴的标定更加复杂。针对MEMS 三轴加速度计的制造误差和安装误差，常用的标定方法有静态24 位置法、静态12 位置法、静态9位置法、重力场静态翻滚法及6 位置法等［3～7］。针对以上问题，且考虑到实际标定的复杂程度，本文基于六位置法研究了MEMS三轴加速度计误差标定与补偿方法，通过卡尔曼滤波（Kalman filtering，KF）算法减小测量噪声，根据MEMS三轴加速度计的输入输出误差模型，建立基于六位置法的误差补偿数学模型及补偿参数求解方法。

1 MEMS三轴加速度计KF算法与误差补偿数学模型

1.1 KF算法

对于无外部输入控制量的线性离散动态系统，系统状态方程和观测方程分别为［8］

式中Xk为系统在k时刻的状态向量，Ak为系统从k时刻到k+1时刻的状态转移矩阵，Wk为系统在k时刻的动态噪声；Zk为系统在k时刻的观测向量，Hk为系统在k时刻的观测矩阵，Vk为系统在k时刻的观测噪声；Wk，Vk为互不相关的均值为0 的高斯白噪声，其在k时刻的协方差矩阵分别为Qk，Rk。

系统状态转移矩阵、观测矩阵、动态噪声、观测噪声均可认为是固定值（即Ak＝A，Hk＝H，Wk＝W，Vk＝V），因此可得到MEMS三轴加速度计的KF 方程为：1）状态向量预测方程为＝；2）状态向量协方差矩阵预测方程为Pk｜k+1＝APk-1AT+Q；3）KF 增益方程为Kk＝Pk｜k-1HT（HPk｜k-1HT+Rk）-1；4）状态向量更新方程为+Kk（Zk-）；5）状态向量协方差矩阵更新方程为Pk＝（I-KkH）Pk｜k-1。其中，为根据k-1 时刻的三轴状态估计向量预测得到的k时刻的三轴状态预测向量，为k-1时刻的三轴状态估计向量，Pk｜k-1为由k-1 时刻到k时刻的三轴状态预测误差协方差，Pk-1为k-1 时刻的三轴状态估计误差协方差。

1.2 误差补偿数学模型

根据MEMS三轴加速度计的主要误差来源及特点，可将MEMS三轴加速度计的输出误差数学模型表示为［6～12］

式中Gx，Gy，Gz为MEMS三轴加速度计的测量值，gn；gx0，gy0，gz0为MEMS 三轴加速度计的零偏值，gn；gx，gy，gz为MEMS三轴加速度计的理论值，gn；Sgxx，Sgyy，Sgzz为MEMS三轴加速度计的刻度因子系数；Kgxy，Kgxz，Kgyx，Kgyz，Kgzx，Kgzy为MEMS三轴加速度计的安装误差系数（含三轴非正交误差系数）；Kgx2，Kgy2，Kgz2为MEMS三轴加速度计二阶非线性误差系数。

对于大部分MEMS三轴加速度计，其二阶非线性误差系数很小，标定与补偿时可忽略不计［13］。因此，不考虑MEMS三轴加速度计二阶非线性误差，可由式（2）得到简化后的MEMS三轴加速度计输出误差数学模型为

为了便于计算误差补偿参数，将式（3）变换为

K3×3为MEMS三轴加速度计的综合误差系数矩阵，为3阶满秩方阵，可逆，则有

不考虑温度变化影响，其综合误差系数矩阵K3×3及零偏误差可视为固定值，因此，式（5）可变换为

式中Gx0，Gy0，Gz0为待求取的MEMS三轴加速度计的零偏误差值，gn；Sxx，Syy，Szz为待求取的MEMS 三轴加速度计的刻度因子系数；Kxy，Kxz，Kyx，Kyz，Kzx，Kzy为待求取的MEMS三轴加速度计的安装误差系数（含三轴非正交误差系数）。

为便于求解误差补偿参数，由式（6）可得MEMS 三轴加速度计误差补偿数学模型为

采用向量、矩阵表示方法，则为

2 MEMS三轴加速度计的六位置标定与补偿

2.1 六位置标定方向与步骤

本文采用自主研发的三维电子罗盘辅助开展MEMS三轴加速度计的标定与补偿研究。实验时，采集经过KF输出的MEMS三轴加速度计数据，在重力场下采用6 位置翻滚完成对MEMS三轴加速度计的标定，根据MEMS三轴加速度计的误差数学模型，以及标定测量得到的6 个位置下的三轴重力分量值，求解误差数学模型中的误差补偿参数矩阵。MEMS三轴加速度计理论输出与6 个位置的对应关系如图1所示。

图1 MEMS三轴加速度计理论输出与6 个位置的对应关系

六位置标定方法的具体标定步骤如下：1）先将电子罗盘安装在三轴无磁转台上，保证电子罗盘各敏感轴方向与三轴无磁转台一致，调整三轴无磁转台处于水平状态；2）接通电子罗盘电源，预热3 min后，开始对MEMS三轴加速度计进行标定；3）调整转台，保证MEMS 三轴加速度计分别处于如图1 中的位置1，2，…，6；4）标定过程中，调整到每个位置后保持静止30 s，然后在静止状态下采集MEMS三轴加速度计的三轴输出数据，数据采集持续30 s。

2.2 六位置标定误差补偿数学模型

根据式（8）及六位置标定数据，可推导得出MEMS三轴加速度计的六位置标定误差补偿参数矩阵求取模型为

3 实验结果与分析

3.1 KF算法验证

从图2实验结果中可以得出，经过KF 后，MEMS 三轴加速度计的输出数据噪声标准差由0. 005 3gn减少为0.001 4gn，输出数据噪声减小了74%，满足标定实验对输出数据噪声的要求。

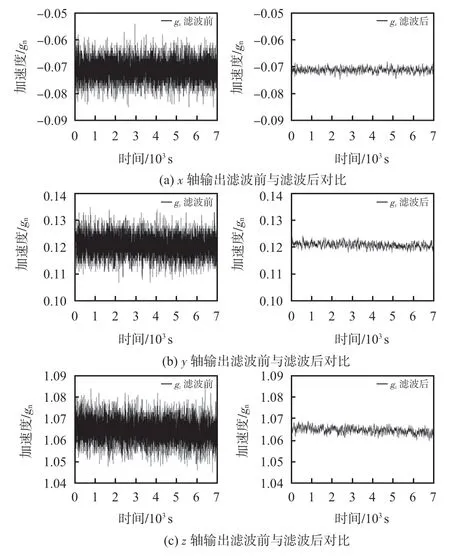
图2 MEMS三轴加速度计滤波前与滤波后对比

3.2 标定实验分析

按照2.1节中的标定步骤对MEMS三轴加速度计进行标定实验，并采集经过KF输出的实验数据，再根据式（10）计算MEMS三轴加速度计的六位置标定误差补偿参数矩阵A4×3。MEMS 三轴加速度计的六位置标定数据如表1所示。

由式（10）可得，MEMS三轴加速度计的六位置标定误差补偿参数矩阵为

从而可求得式（6）中的综合误差补偿系数矩阵和零偏误差补偿值，则有

由表1及式（12）可知，MEMS三轴加速度计存在较大的零偏及灵敏度误差，且三轴灵敏度均偏大，其中，y轴与理论值1相差最大，差值为0.039 0，约3.9%；各轴灵敏度相差最大值为0.030 7，约3.1%；零偏最大值-0.117 6gn；位置3姿态下，y轴偏差达到了0.165 0gn。

由图3可知，标定后六位置下的误差明显减小，标定后位置3和位置4偏差最大，偏差值为0.003 5gn。相较于标定前的0.165 0gn，测量精度提升了将近2个数量级。

图3 六位置标定补偿前与补偿后MEMS加速度计误差对比

3.3 标定结果验证

当进行俯仰角多位置验证时，保持转台横滚角处于0°刻度位置，同时从-90°～+90°以10°步长调整转台俯仰角刻度位置，记为姿态位置1～19；当进行横滚角多位置验证时，保持转台俯仰角处于0°刻度位置，同时从-90°～+90°以10°步长调整转台横滚角刻度位置，记为姿态位置20～38。

俯仰角多位置验证实验加速度计的三轴分量理论值为

横滚角多位置验证实验加速度计的三轴分量理论值为

求解得到电子罗盘的俯仰角α和横滚角β分别为

根据图4可以看出，标定前y轴的零偏误差及灵敏度误差最大，x轴次之，z轴最小，与3.2 节中标定实验分析一致；标定前y轴正负方向测量的灵敏度存在明显偏差，x轴次之，z轴最小；经过六位置标定后，MEMS三轴加速度计的三轴输出值几乎与理论值一致。

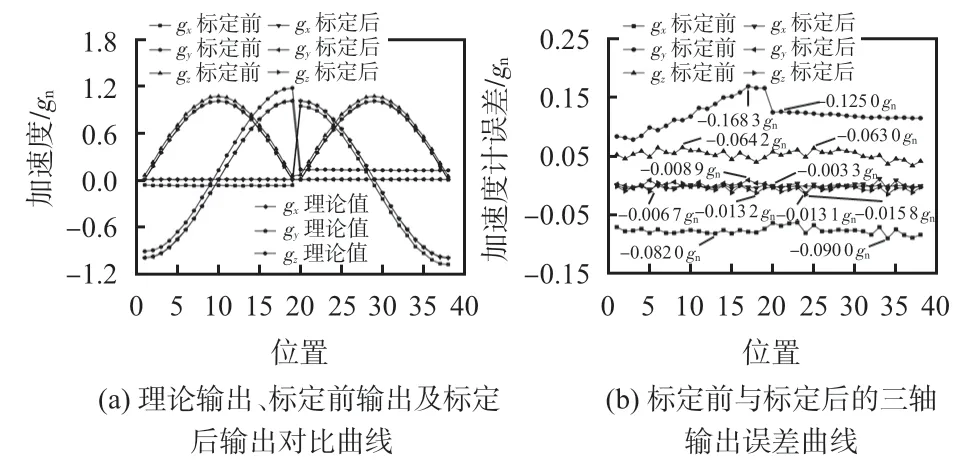
图4 多位置下MEMS三轴加速度计的输出及误差曲线

根据图4（b）可知，标定后的MEMS三轴加速度计误差明显减小，其中，x轴的误差由标定前的-0.0900gn减小为-0.0131gn，y轴的误差由标定前的0. 168 3gn减小为0.008 9gn，z轴的误差由标定前的0. 064 2gn减小为-0.015 8gn，标定后的测量精度提升了1 个数量级。另外，在零偏误差补偿方面，x轴的零偏误差标定前约为-0.082 0gn，标定后约为-0. 006 7gn，标定后减小了91.8%；y轴的零偏误差标定前约为0.125 0gn，标定后约为0.0033gn，标定后减小了97.4%；z轴的零偏误差标定前约为0.057gn，标定后约为0.0042gn，标定后减小了92.6%。

图5 可以看出，在倾斜角度为-90°～+90°，倾斜角精度由标定前的5.9°RMS提高为0.3°RMS，倾斜角精度提升了1个数量级；标定前俯仰角测量最大误差为7.55°，标定后为0.78°；标定前横滚角测量最大误差为8.30°，标定后为0.92°；标定前俯仰角和横滚角均存在明显的零偏误差，其中俯仰角零偏误差由6.35°减小为0.12°，误差减小了98.2%，横滚角零偏误差由4.14°减小为0.05°，误差减小了98.8%。

图5 MEMS三轴加速度计标定前与标定后的倾斜角误差

此外，根据图5可以得知，由于三轴非正交误差和安装误差的影响，在标定前，随着俯仰角或横滚角的变化，横滚角或俯仰角存在漂移误差，其中，当俯仰角由-90°变化为90°时，横滚角由-4.73°变化为-3.74°，变化了1.00°，标定后横滚角变化缩小为0.08°；当横滚角由-90°变化为90°时，俯仰角由7.71°变化为5.94°，变化了1.77°，且此时的二次项系数不可忽略，标定后俯仰角变化缩小为0.04°。

4 结 论

本文方法不仅能减小数据输出噪声，还能有效地补偿MEMS加速度计自身零偏、刻度因子、非正交及安装误差。实验结果表明，经过KF后，MEMS三轴加速度计数据输出噪声减小了74%；经过六位置法标定后，MEMS 三轴加速度计的测量精度提升了1 个数量级，解算得到的倾斜角精度由5.9°RMS提高到了0.3°RMS。该方法补偿精度较高，操作简单，易于实现，具有重要的工程实用价值。