山地微型桩单桩抗压承载机理及数值模拟

温永亮, 黄大志, 陈 朔, 陈 盟, 雍文涛

(1.国网安徽省电力有限公司黄山供电公司,安徽 黄山 245241;2.合肥工业大学 土木与水利工程学院,安徽 合肥 230009)

0 引 言

微型桩是一种新型的直径较小的钻孔灌注桩,是基于树根桩而发展形成的[1],其直径通常小于400 mm,但长细比较大(一般大于30)。微型桩的一般施工步骤是:①首先使用小型的钻机在地面进行钻孔作业;②之后将设计所需的钢筋笼和注浆管放置到孔位之中;③最后采用压力注浆或者灌注细石混凝土的方法成桩。与传统的灌注桩基础相比,微型桩基础的优点主要是施工机具轻便、施工周期较短,施工过程中节省材料、泥浆排放较少、更加环保等。作为一种新型、环保的小型桩基础,微型桩具有很高的研究和应用价值。目前,微型桩在许多领域都有广泛应用[2],例如:①成为基础托换加固的重要手段[3];②旧房改造,房屋加层工程[4];③古建筑物加固纠偏,如利用微型桩对受到破坏的历史建筑物和古迹进行加固[5];④建(构)筑物加固防震工程;⑤水池抗浮,堤岸加固工程;⑥基坑开挖工程。

近年来,很多学者对微型桩基础进行了理论研究和试验研究,包括研究微型桩的抗压、抗拔、水平承载特性,以及群桩效应和动力响应等问题。Das[6]通过试验进行分析,得到桩-土摩阻力随着上层深度的增加呈现出线性增长的趋势,推出桩的临界埋深率(L/d)cr的大小与上体的相对密度Dr有关。Brown Dan A等[7]利用三维有限元模型对某一行或两行的横向荷载作用下的近间隔桩进行了分析,并利用该模型对一排桩之间的距离对桩间弯曲应力产生的p-y曲线的影响进行了分析,分析结果为桩体周围塑性变形区域的变形规律和发展提供了深入的认识。Shin等[8]对微型桩进行了相关的试验,以此分析长细比对微型桩抗拔承载力的影响,提出了微型桩在饱和黏土中的抗拔承载力的经验公式。黄锋等[9]进行了渗水力土工模型试验,对竖向承载桩在桩顶下压、桩顶上拔及桩底上托等承载情况下的桩侧摩阻力的发展规律进行了试验研究,得到了摩阻力与位移的关系、摩阻力强度沿桩身的分布以及摩阻力强度和相应截面位移之间的关系。Liew S S等[10]总结了微型桩的分类、设计理念,以及常见的安装方法等问题;同时也讨论了微型桩的施工控制、系统性能,以及高强度工作荷载下钢筋与砂浆的应变协调性问题;还介绍了微型桩试桩的静载试验结果。一般来说,微型桩相比其他打桩系统的残余沉降更小。龚健[11]将室内试验和现场的施工实践进行结合,总结出了一套适用于实际工程的施工技术;并通过在现场进行原型试验,对单桩和群桩的受力性能进行了描述,表明微型桩在承受荷载时能够有比较好的承载能力;推导出单桩在承受上拔荷载时的变形特性,同时在单桩的基础上研究了多根桩的情况下的群桩效率和其承载性能。吕凡任等[12]在施工现场开展了微型桩群的抗压和抗拔试验,研究了其Q-S曲线关系、群桩效应以及施工技术等,为微型桩的设计和施工提供参考和依据;同时分析上拔和下压荷载下微型桩的受力机制,初步总结出可用位移为20 mm时所受承载力为抗拔和抗压的极限承载力,斜桩可以更好地承担上拔荷载。

目前,随着微型桩基础相关的施工技术的不断完善和发展,微型桩基础的工程应用已经不再局限于传统的边坡治理和基础加固等领域,微型桩的应用范围也已经被扩展到软土地基的杆塔基础施工中。然而,目前微型桩基础被应用于输电线路工程中的案例还比较少,更多的是进行现场真型试验,没有具体的相关设计方法。同时,在施工过程中桩体的几何参数也无具体的标准,这导致现场施工随机性较大。同时,考虑到输电线路工程的施工场地多位于山地,地质条件表现为“上土下岩”的特征,而目前对于微型桩的研究多集中在单一土层的地质条件下。在山地“上土下岩”的特殊地质条件下,确定微型桩的极限承载能力是较为困难的,目前这方面的研究也较少,对于微型桩的变形特性、承载性能、影响因素等方面还没有充分的认识,同时缺乏成熟的系统性的计算理论总结。

综上所述,有必要对应用于输电线路工程施工的微型桩基础进行进一步的分析研究,为类似工况下的微型桩基础的工程设计和应用提供相关的理论依据。因此,本文对山地“上土下岩”的特殊地质条件下,微型桩的极限承载能力开展进一步研究,对微型桩单独承受下压荷载的极限承载能力进行了理论推导,提出了极限承载力和极限变形的计算方法。同时,本文使用ANSYS有限元软件,对一个具体的微型桩模型进行了数值模拟,与理论计算结果进行了对比。

1 下压荷载作用下微型桩极限状态计算

当微型桩的顶部受到下压荷载的作用时,桩身的压应力首先产生在桩顶,桩体与土体之间产生相对位移。因此,微型桩受到的下压荷载会通过桩身与土体之间的剪应力传递到土体中去,从而以桩侧摩阻力的形式表现出来,其传递方向为从上到下。[1]由于微型桩长细比较大,属于摩擦型桩,因此可以忽略桩底土体对桩身的作用力。随着下压荷载的逐渐增大,上部桩身与土层之间的接触面的摩阻力首先达到极限。之后,上部的摩阻力将保持在极限值不再增大,下部桩身与土层的接触面的摩阻力逐渐增大并达到极限。最终,桩侧各处摩阻力都达到极限,使微型桩处于受压极限状态。

1.1 基本假定

对于微型桩的桩身,假定其为线弹性材料,并忽略径向的变形,认为其仅存在轴向的压缩变形。

如图1所示,微型桩位于上土下岩的地层中,其形状为圆柱体,桩径为d,桩长为h,位于土层中的长度为h1,位于岩石层中的长度为h2,下压力作用于微型桩顶部,下压力大小为P,微型桩自重为G,总的摩阻力为f,土层中的摩阻力为f1,岩石层中的摩阻力为f2。

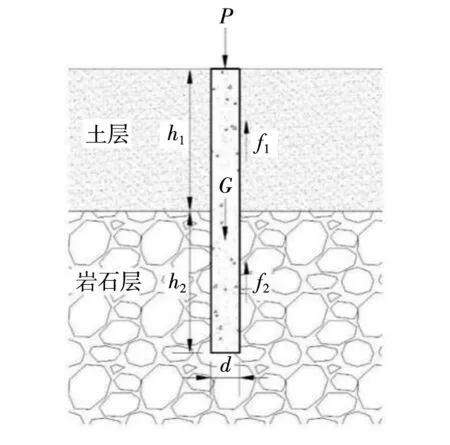
图1 微型桩受压剖面图

对桩侧的土体(岩石),这里参考任珊等[32]采取的方法,有如下假定:①假设桩侧的土体(岩石)是各向同性、质量均匀的,将其视为半空间的理想弹性体;②桩侧土体的固结状态为正常固结;③桩侧土体(岩石)的物理力学性质不会因为微型桩的存在而发生变化。对于抗压微型桩,其在下压荷载、竖直向上的桩侧摩阻力和竖直向下的重力三者共同作用下达到平衡状态。

对于桩侧土与桩身的接触面,其上的切应力τ是一个与桩的轴向位移ω有关的函数。对此,假定其为线弹性全塑性传递函数,土层中的τ-ω图像如图2(a)所示,岩石层中的τ-ω图像如图2(b)所示。

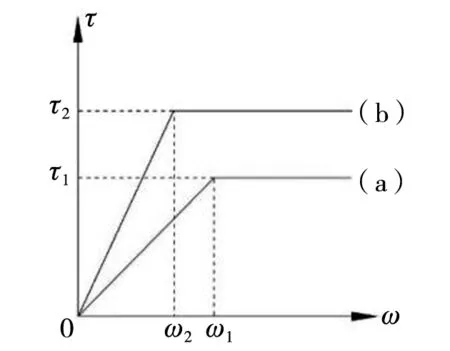
图2 土层和岩石层中的τ-ω图像

τ与ω的函数关系式为:

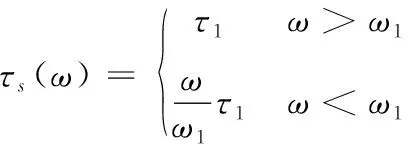
(1)

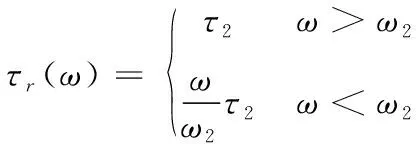
(2)

式中:τs(ω)为土层中τ与ω的函数关系;τr(ω)为岩石层中τ与ω的函数关系;τ1为土层中的最大切应力;τ2为岩石层中的最大切应力;ω1为土层中的最大切应力对应的最小变形量;ω2为岩石层中的最大切应力对应的最小变形量。

对于土层,其最大切应力与土层参数有如下关系:

τ1(z)=c+kszγstanφ

(3)

式中:τ1(z)为土层中最大切应力沿深度z变化的函数;z为深度;c为土的黏聚力;ks为土的侧压系数;γs为土的重度;φ为土的内摩擦角。

实际计算中取土层的平均最大切应力为:

(4)

式中:h1为微型桩在土层中的长度。

对于岩石层,其切应力不会超过岩石的抗剪强度,则岩石层中的最大切应力可以取岩石的抗剪强度,可通过试验进行测定。

1.2 极限抗压承载力计算

在计算微型桩的抗压承载力时,需要根据桩侧摩阻力沿深度变化的函数,通过积分计算出总的桩侧摩阻力

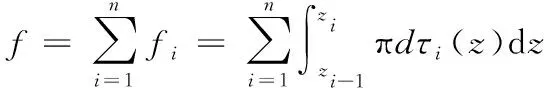
(5)

式中:n为土(岩)层总数;fi为第i层土(岩)中的桩侧摩阻力(i=1,2,3,…);d为桩径;zi为第i层土(岩)底部的计算深度(z0=0,zn为桩底的深度);z为深度;τi(z)为第i层土(岩)中桩侧摩阻力沿深度z变化的函数。

桩侧摩阻力沿深度的分布状况,随着下压力的增大而不断变化。但τ沿深度z变化的函数表达式未知,可认为τ先沿深度z线性变化[5],增大到极限值后保持不变。对于上土下岩地质状况下的微型桩,当下压力P增大到一定程度时,桩侧表面各处的切应力都会达到极限值,此时总的桩侧摩阻力也达到极限值,可得:

fu=πd(h1τ1+h2τ2)

(6)

从而得出微型桩的极限抗压承载力为:

(7)

式中:Pu为微型桩的极限抗压承载力;fu为微型桩的极限摩阻力;G为微型桩的自重;d为微型桩的直径;h1为微型桩位于土层中的长度;h2为微型桩位于岩石层中的长度;τ1为土层中的极限切应力;τ2为岩石层中的极限切应力;γ为微型桩的平均重度。

1.3 极限压缩变形计算

当微型桩的下压荷载达到极限时,微型桩桩身轴力图如图3所示。

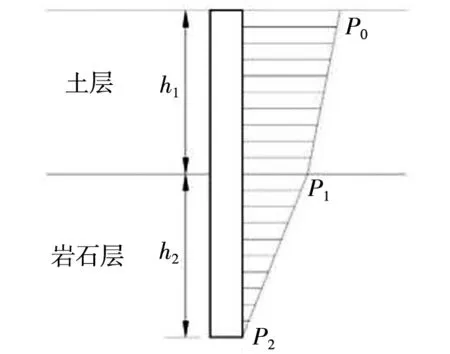
图3 微型桩受压轴力图

其中,桩顶处的轴力大小为:

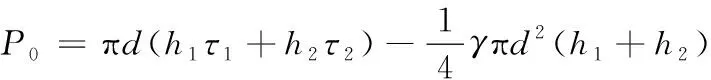
(8)

岩土分界面处的轴力大小为:

(9)

桩底处的轴力大小为:

P2=0

(10)

根据材料力学,有:

(11)

式中:Δl为轴向变形;F为轴力;l为长度;E为弹性模量;A为横截面积。

对于微型桩的压缩变形,使用微分法,得:

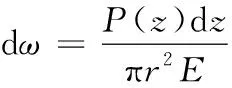
(12)

式中:ω为微型桩的轴向压缩变形;P(z)为轴力沿深度变化的函数;z为深度;r为微型桩的半径;E为微型桩的弹性模量。

求积分,可得微型桩的极限压缩变形为:

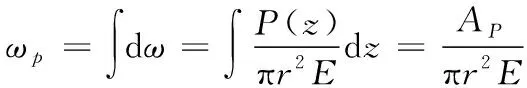
(13)

式中:ωp为微型桩的极限压缩变形;AP为受压轴力图的面积。

根据图3计算轴力图面积得:

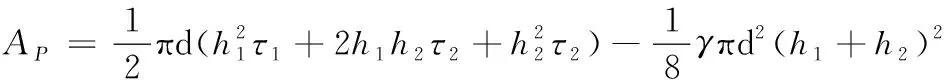
(14)

则微型桩的极限压缩变形为:

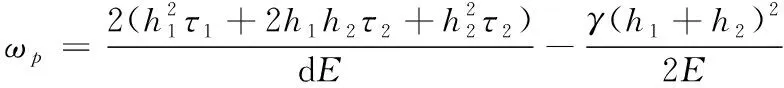
(15)

2 理论计算与数值模拟对比

某工程的微型桩位于上土下岩的地层中,相关参数如表1所示,需要计算此微型桩的极限抗压承载力及变形。

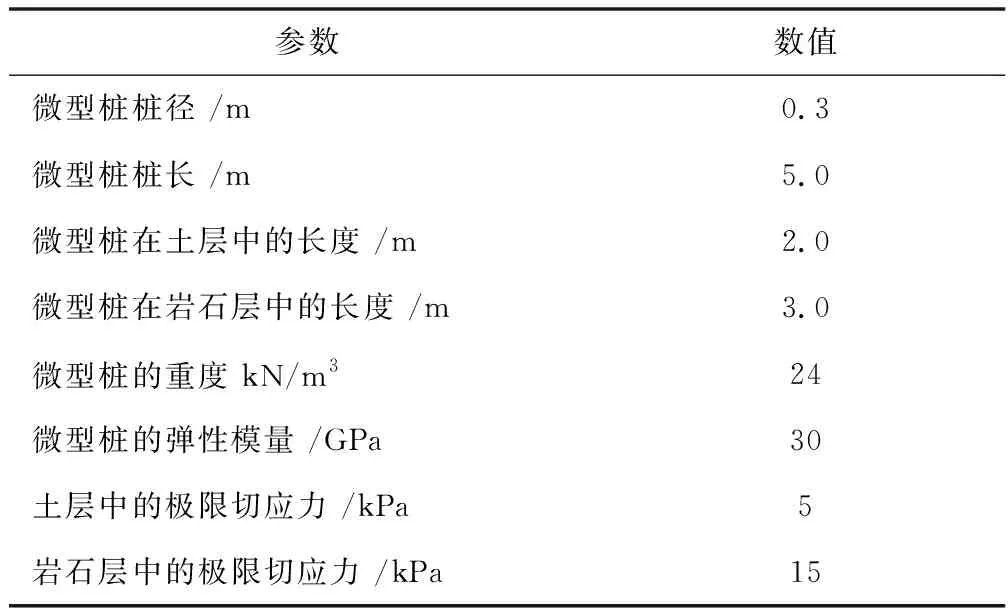
表1 某工程相关参数

2.1 理论计算

根据式(7)、式(15),代入数据,计算得此微型桩的极限抗压承载力为43.35 kN,极限压缩变形为7.34×10-4,则可得最大压应力为613.33 kPa,最大压缩应变为1.47×10-4。

2.2 基于ANSYS的数值模拟

利用ANSYS有限元软件模拟微型桩的受力情况,桩身单元类型选择concret65单元,采用四边形网格划分,最大单元边长为0.1 m,设置混凝土材料的弹性模量为E=30 GPa,泊松比为μ=0.2。微型桩的边界条件选取顶部固定的形式,模型假设微型桩桩身材料各向同性、均质、密实。土层与微型桩的作用,采用表面效应单元进行模拟,单元类型选择surf154单元,采用四边形网格划分,最大单元边长为0.1 m,对其施加5 kPa的切应力用来模拟桩侧摩阻力。岩石层与微型桩的作用,同样采用表面效应单元进行模拟,单元类型选择surf154单元,采用四边形网格划分,最大单元边长为0.1 m,对其施加15 kPa的切应力用来模拟桩侧摩阻力。从而得到微型桩极限受压状态的应力云图如图4(a)所示,应变云图如图4(b)所示。

图4 微型桩极限状态的应力应变云图

由图4(a)、图4(b)可知:在极限受压状态下,微型桩所受最大压应力大小为627.88 kPa,最大压缩应变为1.49×10-4。数值模拟结果与理论计算结果相近,见表2。

表2 理论计算与数值模拟数据对比

3 理论计算与试验数据对比

根据董梅等[13]完成的微型桩下压承载力特性的模型试验,该试验所用的微型桩参数如表3所示,该试验的土层仅有一层,极限摩阻力为13 kPa。

表3 下压试验的数据对比

根据式(7),代入数据,计算该试验的两根微型桩的极限抗压承载力,并与该研究的试验与计算值进行对比,见表3。

从表3可以看出,使用本文所提出的计算方法,计算结果更为接近试验值。

4 结 论

本文考虑了微型桩自重、桩身的压缩变形、桩侧摩阻力,对山地“上土下岩”特殊地质条件下微型桩的抗压承载能力进行了研究,推导得出了微型桩的极限抗压承载力和变形的理论公式,结果表明:

(1) 微型桩处于受压极限状态时,桩侧土和岩石对桩身的摩阻力达到最大值。

(2) 微型桩的极限抗压承载力与土层中的极限摩阻力、岩石层中的极限摩阻力、桩在土层中的长度、桩在岩石层中的长度、桩径、桩的重量有关。

(3) 微型桩的极限压缩变形不仅与上述因素有关,还与桩身的弹性模量有关。