大型高层建筑结构构件可靠度综合评估模型构建

何卓应

(广东诚实建设工程设计有限公司,广东 梅州 514000)

0 引 言

大型高层建筑结构由于其复杂性和特殊性,面临着多种潜在的风险和挑战。质量问题、自然灾害、设计和施工缺陷等都可能导致结构的失效或损坏。对于大型高层建筑而言,其稳定性在很大程度上取决于建筑结构构件的可靠性。[1]在对该指标进行评估时,考虑到不同建筑结构自身构成的特殊性[2],要实现对其的综合评价首先需要对构件的属性以及结构特点进行分析[3],在此基础上,结合构件的目标应用环境,对其可靠性作出全面分析。[4]通过构件可靠度的综合评估,可以准确识别结构中的薄弱环节和潜在风险,从而采取相应的措施来提高结构的可靠性和安全性。因此,对于大型高层建筑结构的可靠性综合评估成了一个重要的研究方向。

许多研究人员对该方面进行研究,如:文献[5]以FRP筋混凝土为研究对象,分析了受弯构件在裂缝控制作用下的可靠度,分析结果具有一定的准确性,但是其在具体的应用过程中对基础结构构成的要求较高,因此应用范围相对有限。文献[6]以内置型钢钢管混凝土轴压构件为研究对象,在对其进行设计的基础上,对相应可靠度分析方法进行研究,大大提高了分析结果的准确性,但是同样地,其在应用阶段的局限性相对较强。文献[7]将贝叶斯更新融入在役钢筋混凝土桥梁构件可靠度的分析研究综合,并通过与逆高斯过程进行有机结合,实现了随着时间的推进,对构件可靠度的动态预测,并且预测结果具有较高的准确性,但是值得关注的是,由于在运行过程中构件受到的外力作用并非恒定不变,因此该方法对突变情况下的可靠性分析结果存在优化空间。通过对上述关于建筑构件可靠性分析方法的研究可以看出,加深对该问题的研究仍然对于现实施工具有重要的指导价值。

在上述研究的基础上,本文以大型高层建筑结构构件为研究对象,构建了以可靠度综合评估为目标的模型,并通过试验测试的方式分析验证了设计模型在实际应用中的价值。借助本文构建的模型,希望可以为实际的工程建设提供有价值的参考,最大限度保障建筑结构的稳定性和安全性。

1 建筑结构构件可靠度综合评估模型设计

1.1 建筑结构构件可靠度评价指标构建

要确保构建的大型高层建筑结构构件可靠度综合评估模型能够真实准确地反馈构件的实际情况[8],首先需要对构件具体的可靠度评级指标进行合理设计。一般情况下,建筑结构构件的可靠性是不能够直接应用的。作为一个相对定性化的指标参量,需要借助可靠度这一指标实现对其的度量[9,10]。在此基础上,本文将构件在规定时间和条件下完成设计功能的概率作为结构可靠度的评价指标。那么对应地,结构在规定时间和条件下,不能完成设计功能的概率即为结构的失效概率。根据可靠度分析理论可知,建筑结构构件的状态可以表示为“可靠-失效”的二级化模式,可靠度代表了构件在给定使用条件下,不发生失效的能力。而失效概率则是衡量构件在给定时间内发生失效的可能性。可靠度和失效概率是互为补充的概念,失效概率是可靠度的补数。构件的安全状态和失效状态是以独立对立的形式存在的,这种互不相容的关系使得构件的可靠度和失效概率之间的存在以下关系:

Kw+Pl=1

(1)

式中:Kw为构件能够在规定时间和条件下完成设计功能的概率值,Pl为构件无法在规定时间和条件下完成设计功能的概率值。以此为基础,构件整体的可靠度就可以用上述两个参数进行表述。但是需要注意的是,虽然从整体上分析影响建筑结构构件可靠度的因素仅分为上述两个指标,但是在实际的施工过程中,上述两个因素是以相对宏观的形式表现的。这就意味着Kw和Pl均是由相关施工条件、构件加工条件以及构件应用条件等因素共同作用形成的。针对该问题,为了进一步提高建筑结构构件可靠度评价指标的应用价值,需要对其进行进一步细化。

为此,本文假设影响建筑结构构件可靠度的因素为随机变量,以构件为目标对象的环境中,各影响因素的联合概率密度函数可以表示为:

f(X)=f(x1,x2,…,xn)

(2)

式中:f(X)为建筑结构构件各影响因素的联合概率密度函数,xn表示任意影响建筑结构构件可靠度的因素,通过式(2)可以看出,存在X={x1,x2,…,xn},那么对应地,建筑结构构件的可靠度评价指标可以表示为:

∑Kw(xn)+∑Pl(xn)=n

(3)

式中:n为参与建筑结构构件的可靠度评估的影响因素总量。

按照这样的方式,即可实现对建筑结构构件可靠度评价指标的构建,为后续评估模型的设计提供基础。

1.2 建筑结构构件可靠度评估模型构建

在确定具体的评价指标后,本文在建筑结构构件可靠度评估模型构建阶段的主要任务就是明确Kw和Pl对构件可靠度影响权重的大小。需要注意的是,不同建筑构件无论是在基础材料组成上,还是具体的应用设计上都存在对应的差异性,也正是因为这种差异性,直接以定量化的参数对其可靠度影响权重进行计算难以计算得到准确的可靠度结果。为此,本文采用二阶弹性分析设计法实现对其可靠度评价指标权重的计算。

对建筑结构构件可靠性进行计算的最终目标是提高分析结果的准确性,本文通过在各层柱顶附加假想水平荷载的方式得到各个影响因素在二阶弹性分析设计法下的影响程度。在此基础上,再综合考虑构件结构中存在的整体几何缺陷对可靠度的作用强度。不仅如此,为了避免由于构件长度差异对验算结果的影响,本文以1.0作为统一长度系数。这样也可以在一定程度上简化对构件可靠性评价因素权重计算的复杂性。具体的二阶弹性分析设计法计算结果可以表示为:

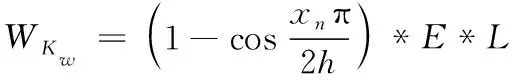
(4)

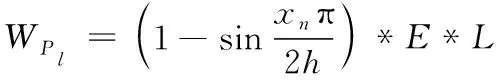
(5)

式中:WKw为Kw在建筑结构构件可靠度评估中的权重系数,WPl为Pl在建筑结构构件可靠度评估中的权重系数,L为构件长度。根据上述的设置,式(4)和式(5)中的L均取1.0。E表示施加在建筑结构构件各层的水平荷载强度,考虑到构件失效是一个逐渐发展的过程中,当作用与构件的荷载强度小于临界荷载力时,构件是以相对稳态的形式存在的,对应的形变量以及内力的变化都是均匀发展的。当作用与构件的荷载强度大于临界荷载力时,构件是以非稳态的形式存在的,对应的形变量以及内力的变化也将呈现出跃进式的发展特点。为此,本文在对E值进行设置时,将其初始变异系数设置为0.2,得到初始临界荷载力阈值范围后,设置E的变异系数为0.1。通过这样的方式,确保最终计算得到的构件可靠性评价因素权重系数无限接近实际值。

按照上述方式计算得到的权重系数,本文构建的建筑结构构件可靠度评估可以表示为:

K=∑WKwKw(xn)-WPl∑Pl(xn)

(6)

式中:K为构件的可靠度评估模型。按照式(6)所示的方式,根据构件的实际应用需求,将对应的影响因素指标输入到模型中,模型输出的结果即为构件对应的可靠度评估结果。

通过这样的方式,实现对构件可靠度的准确计算。

2 实例分析

本文在上述理论设计的基础上,以实际施工案例为基础进行了实例分析,考虑到直接对构件的可靠度进行测量难度较大。因此,本文采用现阶段工程验收中应用的蒙特卡罗法计算得到的结果作为基准。在此基础上,分别采用文献[5]和文献[6]提出的方法作为对照组,通过比较不同方法计算结果与蒙特卡罗法计算对应结果之间的误差,分析本文设计综合评估模型的应用价值。

2.1 建筑结构构架基础参数

本文进行测试的建筑结构构件为平面桁架多构件体系,弹塑性平面桁架的具体施工设计如图1所示。

图1 平面桁架结构示意图

从图1中可以看出,进行测试的弹塑性平面桁架构件由10个基础构件组成,结构整体形态规则,并且平行构件之间设置了加固结构确保其稳定性。按照图1所示,对构件各组成部分的具体性能参数进行分析,其中,各杆件截面屈服强度一致,均为200.0 MPa,单元截面面积均为0.5 m×0.5 m,构件受到的水平荷载力均值为12 500 kN,变异系数为0.35。构件水平和垂直组成部分之间的跨度均为 4 000.0 mm,结构对应的弹性模量为2.0×105N/mm2,挠度不确定性系数为1.07,对应的变异系数为0.02。对构件的施工设计情况进行分析,对应的混凝土强度等级和施工厚度分别为 C30和25.0 mm。

2.2 实验指标

按照上述所示的方式,计算构件的可靠度。可靠度结果误差是评估方法和模型的精确度和准确性的一种度量。较小的误差表示评估方法和模型的可靠度较高,结果更接近真实情况。可靠度结果误差的计算表达式为:

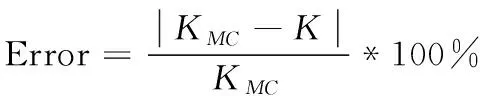
(7)

式中:Error为计算结果的误差,KMC为蒙特卡罗法计算得到的构件可靠度标准解。

2.3 计算结果与分析

在上述测试的基础上,本文统计了不同方法对构件可靠度计算结果,并按照式(7)所示的方式对各个方法对应结果与标准解之间的误差进行计算,得到的数据信息见表1。

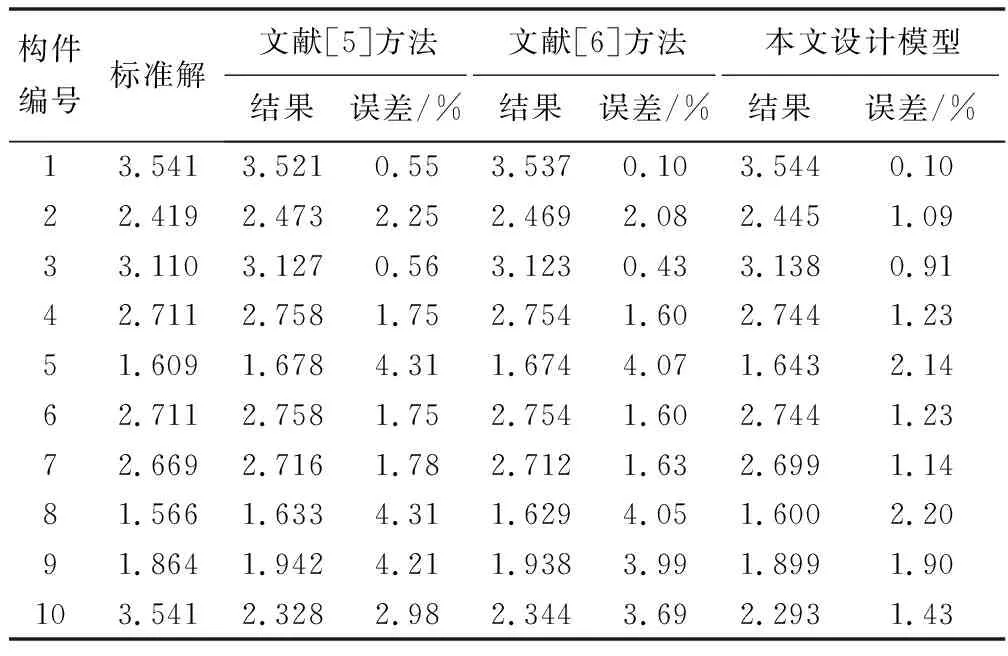
表1 不同方法建筑结构构件可靠度计算结果统计表

通过观察表1中的数据可以看出,对比不同方法对施工构件可靠度的分析结果可以看出,其中,文献[5]方法计算结果与标准解之间的误差表现出了较为明显的不稳定性,其中,最小值仅为0.55%,但是最大值达到了4.31%。文献[6]方法的计算结果与标准解之间的拟合度有所提升,其中,最小误差仅为0.10%,但是最大误差也达到了4.07%,虽然与文献[5]方法相比虽然表现出了一定的优势,但是其仍存在一定的提升空间。相比之下,本文设计模型对测试建筑施工构件可靠度的计算结果与标准解之间的误差始终稳定在2.50%以内,最大值仅为2.20%,最小值仅为0.10%。测试结果表明,本文设计的大型高层建筑结构构件可靠度综合评估模型可以实现对构件应用状态的准确分析,能够为实际的建筑施工提供可靠的数据支撑。

为进一步验证设计方法的实效性,进行建筑结构构件可靠度评估时间测试,测试结果见表2。

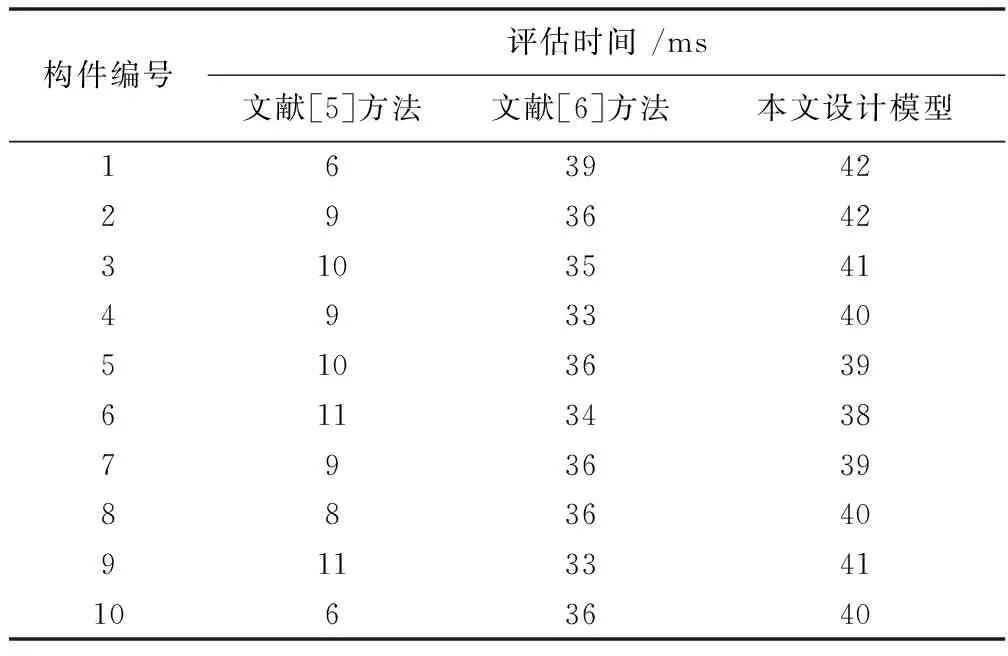
表2 测试结果

根据表2可以看出,本文方法的建筑结构构件可靠度评估时间最高为11 ms;而对比方法的建筑结构构件可靠度评估时间明显高于本文方法,文献[5]方法的建筑结构构件可靠度评估时间最高达到了39 ms,文献[6]方法的建筑结构构件可靠度评估时间最高达到了42 ms。由此可见,本文方法的评估效率较高,具有实用性。

3 结束语

为了最大限度地降低由构件可靠度无法满足建筑需求导致的安全问题,对构件的可靠度进行准确评估分析是十分必要的。考虑到影响其可靠度的因素不仅涉及其自身构成,同时也与其实际应用环境的应力需求之间相关,因此,综合考虑构件的各指标参数与应力能力是保障可靠度计算结果准确性的关键。本文设计了一种大型高层建筑结构构件可靠度综合评估模型,实例结果表明,设计模型对构件可靠度的评估结果与标准解之间的误差最大值为2.20%,最小值仅为0.10%,可靠度评估时间最高为11 ms,说明设计模型实现了对建筑结构构件可靠度准确高效的计算。通过本文的研究,希望可以为相关建筑施工提供有价值的帮助,保障建筑施工的稳定性和安全性。