中外规范基于静力触探的管桩承载力计算方法对比研究

吴磊磊, 唐国喜, 胡胜来

(1.安徽省交通规划设计研究总院股份有限公司,安徽 合肥 230088;2.公路交通节能环保技术交通运输行业研发中心,安徽 合肥 230088)

0 引 言

桩基础是目前广泛采用的一种基础形式,桩基承载力的确定相比浅基础承载力的确定更为复杂和困难,如何将静力触探测试成果应用于桩基工程的勘察和设计中,一直是工程界关注的问题。

确定单桩承载力的方法通常包括以下五种:①静载荷试验;②动力试验;③静力理论公式计算;④根据规范查表;⑤根据原位测试成果计算。其中,静载荷试验法是公认的确定单桩承载力最可靠的方法,是评价其他间接方式的标准,但其费用高、耗费时间较长。在设计阶段尚没有进行静载荷试验的情况下,如何根据勘察成果较准确地确定桩的承载力,是对工程的安全性和经济性均具有重要意义的课题。

目前,国内大多采用查规范表格取得经验参数计算桩基承载力的方法,而国外通常采用原位测试成果进行计算。国内行业规范中的经验参数为全国范围的试验数据经统计分析得到,而我国幅员辽阔,各地区地层分布及性质复杂多变,单纯依靠规范中的经验参数往往与实际存在较大偏差;地方标准中的经验参数也仅来自收集的有限样本,单纯依靠经验参数法也难免不够准确。因此,在设计阶段确定桩基承载力时,同时重视多种勘察手段以及地区经验的作用是很有必要的。

对于管桩而言,静力触探的贯入过程与其成桩过程具有较高的相似性。较多学者尝试采用静力触探成果确定管桩的承载力,均取得了较好的效果。本文试图通过现场试验,对中外规范基于静力触探参数估算管桩单桩极限承载力的经验公式的准确性进行对比分析。

1 规范经验公式

1.1 《铁路工程地质原位测试规程》(TB 10018—2018)

该标准中按下式计算打入式混凝土桩的极限承载力:

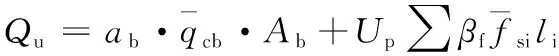
(1)

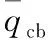
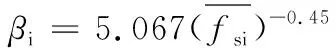
(2)

α=3.975(qcp)-0.25

(3)

(4)

α=12.064(qcp)-0.35

(5)

1.2 “法国LCPC”方法

Bustamante和Gianeslli(1982)对1972年制定的用静力触探估算单桩承载力的方法作了修正,称为“法国方法”,又称“LCPC”法。该方法是Bustamante和Gianeselli基于对不同地基上和不同类型桩的197组载荷试验结果的分析而提出的,其中静力触探测得的侧壁摩阻力fs被忽略,单位端阻和侧阻均从平均锥尖阻力qc得到。

极限桩侧摩阻力qs和极限桩端阻力qp按下式计算:

qs=qc/α

(6)

qp=kcqca

(7)

式中:α和kc分别为摩擦系数和端承系数,根据桩的类型和地基土类确定;qca为等价平均锥尖阻力。

该方法用等价平均锥尖阻力qca来计算单位桩端阻力qp,它是取桩端上、下1.5D(D为管桩的直径)范围内的锥尖阻力qc的平均值。Bustamante &Gianeselli建议分三步来计算qca,首先计算桩端上、下1.5D范围内的qc平均值q′ca;第二步,在桩端上、下1.5D范围内舍弃大于1.3q′ca和桩端以上1.5D范围内低于0.7q′ca的qc值;最后计算剩下的qc平均值,即得到qca。

图1 等价平均锥尖阻力计算简图

打入式预制桩、预应力管桩被归类为第Ⅱ组的A类,其kc值、α值分别按表1、表2取用,其中表2括号内数值为施工质量较好时采用。

表1 打入式预制桩、预应力管桩的kc值

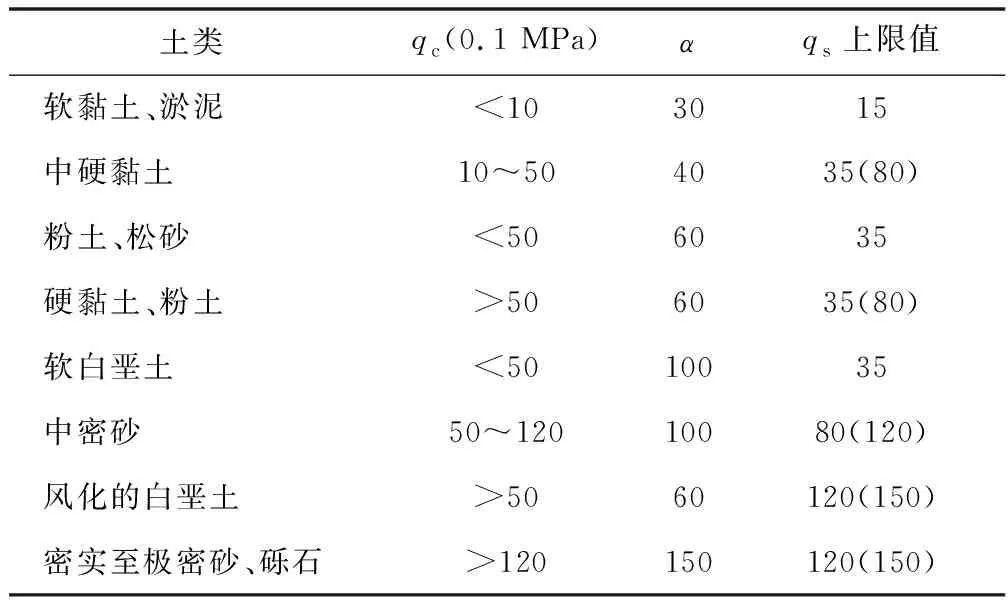
表2 打入式预制桩、预应力管桩的α值及qs上限值

1.3 《建筑桩基技术规范》(JGJ 94—2008)

该标准中按下式计算黏性土、粉土和砂土地层中混凝土预制桩单桩竖向极限承载力标准值:

Quk=u∑liβifsi+αqcAp

(8)

式中:u为桩身周长;li为桩穿越的第i层土的厚度;fsi为第i层土的探头平均阻力;Ap为桩端面积;qc为桩端平面上、下探头阻力,取桩端平面以上4D(D为管桩的直径)范围内按土层厚度的探头平均阻力加权平均值,然后再和桩端平面以下1D范围内的探头阻力进行平均;α为桩端阻力修正系数,对黏性土、粉土取2/3,对饱和砂土取1/2;βi为第i层土桩侧阻力修正系数,按下列公式计算:

对黏性土、粉土:

βi=10.04(fsi)-0.55

(9)

对砂土:

βi=5.05(fsi)-0.45

(10)

1.4 《公路桥涵地基与基础设计规范》(JTG 3363—2019)

该标准中的计算公式与《铁路工程地质原位测试规程》完全一致,区别在于对侧摩阻力设置了限值,即当βfs>100 kPa时,取βfs为100 kPa。

2 现场试验

某管桩工程场地为河流冲积地层,主要土层分布情况及静力触探测试参数平均值见表3。

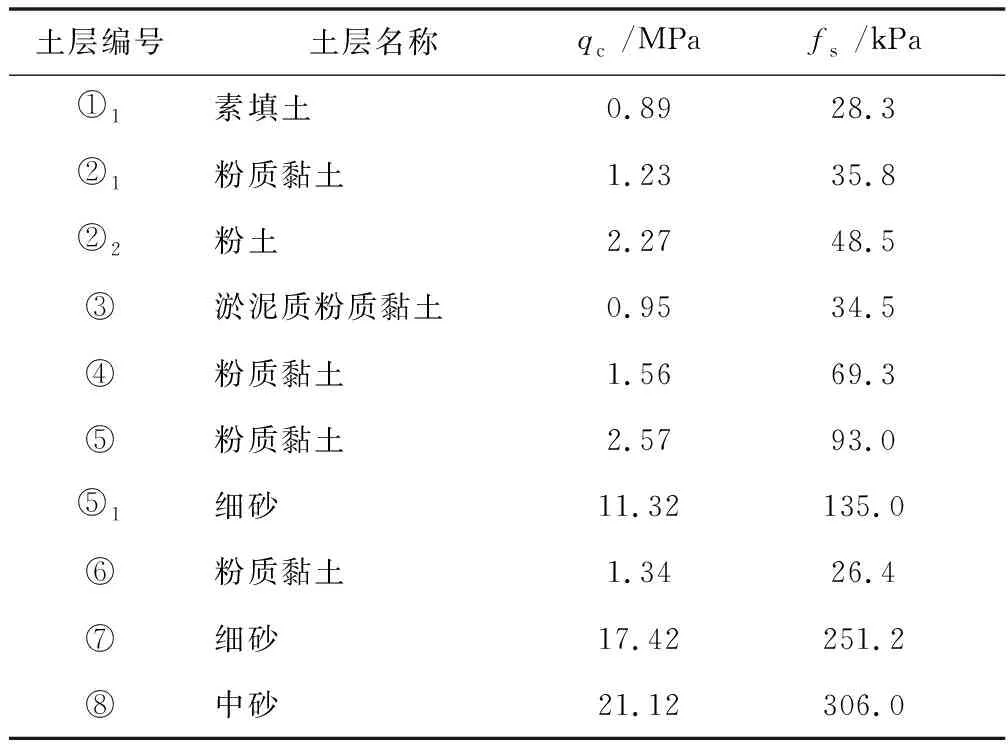
表3 场地土层分布情况及各土层静力触探参数统计值

在该工程场地的9个静力触探孔位置设置了12根管桩试验桩,编号为SZ1～SZ12,管桩型号为PHC500AB(100),除SZ9、SZ10设计桩长为15 m外,其他试验桩的设计桩长均为12 m。试验桩均以⑦层细砂或⑧层中砂为持力层,⑦层细砂、⑧层中砂均为密实状态,桩端进入持力层不小于2 m。

现场施工时,为便于测试工作开展,管桩桩顶预留0.5 m左右在地面以上,SZ9、SZ12因贯入度小或桩顶损伤而终止施工。其中,9根试验桩采用堆载法载荷试验测试管桩单桩极限承载力,另3根桩作为对比试验桩,采用自平衡法测试管桩单桩极限承载力,测试结果见表4。

表4 管桩单桩极限承载力静载荷试验结果

由载荷试验数据可知,本工程上述试验桩的单桩极限承载力均不小于3 000 kN,表中所列承载力的差异为受加载方式、加载荷载值的影响。

3 对比分析

选取该工程场地实施的42份双桥静力触探数据,基于国内《铁路工程地质原位测试规程》TB 10018—2018、《建筑桩基技术规范》JGJ 94—2008、《公路桥涵地基基础设计规范》JTG 3363—2019,以及国外常用的法国LCPC法(《孔压静力触探测试技术规程》T/CCES 1—2017引用该方法)等(以下分别简称为“铁路规程”、“建筑桩规”、“公路桥规”和“法国LCPC”)给出的经验公式,分别计算了各静力触探孔位置的打入桩单桩极限承载力,如图2所示。

图2 不同规范方法的管桩单桩极限承载力计算值

参与计算的样本沿线路方向顺次编号,因此,图中曲线的变化可以近似视为管桩单桩极限承载力沿路线纵向的空间变化。

由图2可知,36例样本根据“建筑桩规”法预测的管桩单桩极限承载力最高,占比达85.71%;34例样本根据“铁路规程”法预测结果最低,占比达76.19%;25例样本根据“法国LCPC”法预测结果居第2位,占比达59.52%。

总体而言,在该工程中,根据“建筑桩规”法预测的管桩单桩极限承载力最大,根据“铁路规程”法预测的最小。

随着路线方向地层的变化,上述四种经验公式方法估算的管桩单桩极限承载力的变化趋势总体上是一致的。

需要注意的是,在样本1、样本31、样本32、样本33处,“法国LCPC”法预测结果均显著低于其他方法,主要和桩端位置等效平均锥尖阻力的计算方法和取值差异有关。

此外,样本31、样本32处管桩单桩极限承载力计算值较其他位置偏低,主要原因在于上部分布有淤泥质粉质黏土层降低了侧摩阻力,以及设定的桩端位置以下一定范围内存在黏性土透镜体,导致端阻力降低。

根据上述标准的经验公式方法计算所得的管桩单桩极限承载力,与现场静载荷试验结果对比情况见表5。

表5 管桩单桩极限承载力计算值与试验值对比

SZ1～SZ12按照“铁路规程”法的单桩极限承载力计试比分布情况如图3所示。

图3 “铁路规程”法的管桩极限承载力计试比频数分布直方图

由图3可知,铁路规程法计算结果75%分布在测试值±10%偏差范围内,83.3%分布在测试值±20%偏差范围内。因此,就测试值而言,“铁路规程”法计算结果准确性高。此外,负偏差比例为75%,其中58.3%的偏差位于-10%以内,且3例正偏差样本均受加载值的限制,实际未达极限状态,因此采用铁路规程法计算管桩单桩极限承载力具有较高的安全度。

SZ1～SZ12按照“法国LCPC”法的单桩极限承载力计试比分布情况如图4所示。

图4 “法国LCPC”法的管桩极限承载力计试比频数分布直方图

由图4可知,“法国LCPC”法计算结果41.7%的偏差位于±10%以内,83.3%分布在测试值±20%偏差范围内。因此,就测试值而言,“法国LCPC”法计算结果准确性较高。此外,正偏差比例为66.7%,该方法总体偏于高估管桩单桩极限承载力。然而,考虑到较多试验桩均受加载值的限制,实际未达极限状态,因此采用铁路规程法计算管桩单桩极限承载力预计具有较高的安全度。

SZ1～SZ12按照“建筑桩规”法的单桩极限承载力计试比分布情况如图5所示。

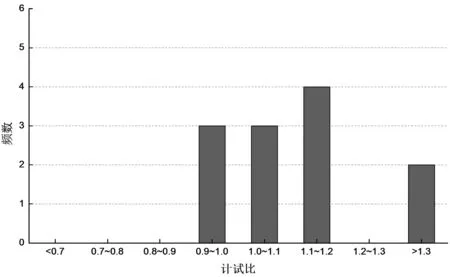
图5 “建筑桩规”法的管桩极限承载力计试比频数分布直方图

由图可5知,建筑桩规法计算结果50%分布在测试值±10%偏差范围内,83.3%分布在测试值±20%偏差范围内。因此,就测试值而言,法国LCPC法计算结果准确性较高。此外,因75%的偏差为正,故该方法总体偏于高估管桩单桩极限承载力。

SZ1～SZ12按照“公路桥规”法的单桩极限承载力计试比分布情况如图6所示。

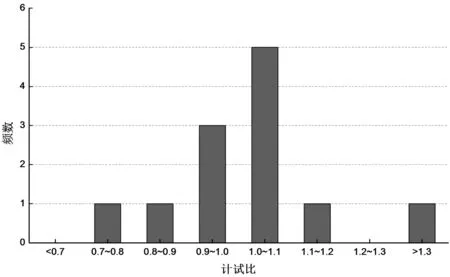
图6 “公路桥规”法的管桩极限承载力计试比频数分布直方图

由图6可知,公路桥规法计算结果呈近似正态分布,66.7%位于测试值±10%偏差范围内,83.3%分布在测试值±20%偏差范围内。就测试值而言,公路桥规法计算结果准确度高。

因此,就实际测试值而言,按偏差分布情况对计算的准确性进行排序为:铁路规程法>公路桥规法>建筑桩规法>法国LCPC法。

需要注意的是,本工程管桩的现场静载荷试验中,其中9根桩未加载至极限状态,因此所列出的单桩极限承载力仍可能是偏于保守的。

此外,试验桩的桩端持力层为密实砂层,桩长也相对较短,端阻力占比较大,因此桩端土层的端阻力、桩侧土层的侧摩阻力均能得到较好的发挥。对于长桩以及桩端持力层非密实砂的情况,荷载传递机制以及土层的承载力发挥作用会存在差异,采用上述规范方法基于静力触探参数估算管桩单桩承载力的准确程度需要另行分析评价。

4 结束语

本文结合现场试验,对中外规范基于静力触探参数估算管桩单桩极限承载力的准确性进行了验证和分析,得到如下结论:

(1) “铁路规程”“法国LCPC”“建筑桩规”“公路桥规”法预测管桩单桩极限承载力均具有较高的准确度,偏差总体在±20%范围内。

(2) 根据本次对比试验的结果,“铁路规程”法的预测精度最高,但因多数试验桩并未加载至极限状态,故“铁路规程”法预测结果偏于安全。

(3) 上述不同方法预测结果的差异主要来源于等效桩端阻力的计算方法的不同,以及侧摩阻力是否设置限值。

(4) 对比分析结果适用于桩端持力层为密实砂层且桩长较短的情况,其他条件下仍需进一步开展研究工作。