一种改进的混合三端输电线路故障定位算法研究

王振杰,姚善化

安徽理工大学 电气与信息工程学院,安徽 淮南 232063

1 引 言

随着城市化进程的发展,输电线路的布局在不断发生着变化。单一的架空线路越来越不适应城市建设的协调,电缆线路能凭借其占地面积小等优点,充分利用城市的空间和土地。因此在城市内大多已经采用电缆线路,而在城市外采用架空线路,逐渐形成架空线-电缆的混合线路分布格局[1-2]。对于架空线路,大多数都是瞬时性故障。而电缆线路深埋在城市地下,故障的概率远远小于架空线。在长期的运行下,由于外部因素会引起绝缘老化而造成永久性故障,因此这将对混合线路故障定位准确性的要求更高[3-4]。

目前国内外对于单一均匀线路的研究达到了很高的水平[5-8],然而架空线和电缆线路的混合线路改变了线路阻抗特性,造成电缆和架空线的波速不一致。在架空线和电缆连接点使得波阻抗不再均匀,行波将产生更加复杂的折反射现象,传统的测距方法也无法直接应用于此[9]。对于混合线路的故障测距仍需要深入研究,文献[10]采用了一种基于小波变换的双端混合线路故障定位,通过采集故障电流行波信号实现精确定位,但定位精度会受到同步时钟的精度和电流传感器采集精度的影响,并且存在小波变换选择小波基函数和分解尺度的难题。文献[11]将传统的波速归一化理论应用于混合线路中,再利用波速和时间差值计算出故障距离,但实际的混合线路参数具有时变特性,因此故障定位的准确性会受到波速的影响。文献[12]和文献[13]均采用了利用CEEMDAN对故障电压行波进行分解并能精确识别行波波头到达检测点时间,但CEEMDAN算法由于存在随机分量,会导致每次分解的数据有偏差。文献[14]提出了一种基于非同步电流测量的故障定位方法,利用第二次行波到达检测端判断故障线段,通过连接在故障线段的检测端计算出故障距离,降低了采集成本,但该方法需要精确的线路参数值,否则会影响定位精度。

现有混合线路的故障检测方法有行波法、故障分析法、人工智能法等。行波法测距的关键问题是能否有效提取波头到达检测端的时间,常用的方法有小波分析法、希尔伯特黄变换等。小波分析法[15]需要选择合适的基函数,不同基函数的选取对最后分析结果的准确性造成影响,不存在哪一种基函数适用于所有场合。希尔伯特黄变换[16]吸取了小波分析的优势、克服了小波分析需要选择小波基的困难,但希尔伯特黄变换存在过包络和欠包络现象,影响整个数据序列。

由于上述算法缺点,本文提出了基于CEEMDAN和Teager-Kaiser能量算子(TKEO)的故障行波定位改进算法。改进CEEMDAN算法有较强的完备性,具有更快的计算速度,能够得到更好的模态分解结果;TKEO算法可以增强信号中存在的高频瞬态并有效地提取信号能量值。将所提改进算法对混合三端线路的故障电压行波进行分解,提取故障行波到达4个检测端的时间,根据零模线模分量的时间差判断出故障区间,推导了基于零模线模分量的双端混合线路行波测距方法并求出故障距离。

2 改进CEEMDAN和TKEO算法

2.1 改进CEEMDAN算法

输电线路在发生故障后的信号具有非平稳性和非线性特征,传统的经验模态分解算法虽能将故障信号分解为单一的固有模态(IMF)分量,但容易出现虚假IMF分量和模态混叠等问题,失去了原有的物理意义。CEEMNAN算法有效地解决了EEMD算法在分解过程中造成每个IMF数量不同的问题[17],但是CEEMDAN算法在分解的早期会出现一些虚假分量造成真实分量出现得较晚。因此,Colominas等学者[18]提出了改进的CEEMDAN(ICEEMDAN),可以将信号的每个分量都提取出来,不会出现虚假分量。然而不论是CEEMDAN或ICEEMDAN,在每一次信号分解的过程中,都是添加了随机分量,这会导致最终提取每次故障行波到达检测点的时间不同,为了增强故障行波信号的突变特性,因此本文在文献[18]研究的基础上,提出一种改进的混合三端输电线路故障定位算法,具体分解步骤如下:

1) 使用EMD计算I个混合信号xi(t)=x(t)+βk-1Ek(ωi(t)),(i=1, 2…,I)的局部均值,以获得第一个残余分量,如式(1)所示:

r1(t)=〈M(xi(t))〉

(1)

其中,x(t)为原信号,βk-1是标准噪声偏差,ωi(t)是遵循N(0,1)分布的高斯白噪声,Ek(·)是定义由EMD分解获得的第k个IMF分量,M(·)是计算局部均值的算子,〈·〉是求平均值的算子。

2) 根据公式(1)求出第一个IMF分量d1(t):

d1(t)=x1(t)-r1(t)

3) 计算第二个残余分量以实现r1(t)+β1E2(ωi(t))局部均值的平均值,并获得第二个IMF分量:

d2(t)=r1(t)-r2(t)=r1(t)-〈M(r1(t)+β1E2(ωi(t)))〉

4) 当k=3,…,I时,计算第k个残余分量:

rk(t)=〈M(rk-1(t)+βk-1Ek(ωi(t)))〉

5) 计算第k个IMF分量:

dk(t)=rk-1(t)-rk(t)

6) 重复步骤4)和5),计算得到所有的IMF分量。

7) 设IMF分量数据为a[i],对各个IMF分量做如下操作:

其中,b[i]是IMF分量a[i]进行一阶差分的结果。

离散信号的一阶差分类同于连续信号的一阶微分。连续函数在奇异点处的微分值常有剧烈波动。离散信号处理中正是根据这一特点利用差分实现奇异点检测。对IMF分量进行差分运算,可以减轻数据之间的不规律波动,使其波动曲线更平稳,增强IMF分量的突变特性,消除CEEMDAN算法引起的随机性问题。

2.2 Teager-Kaiser能量算子

Teager-Kaiser能量算子[19]由Teager和Kaiser提出,是一种非线性的高通能量跟踪算子。它在抑制低频信号的同时增强信号中存在的高频瞬态,因此可以有效地提取信号的瞬时能量。

对于离散信号s(n),TKEO可表示为

ψ[s(n)]=[s(n)]2-s(n-1)s(n+1)

TEKO能量算子的主要特点是其几乎是瞬时的,因为它在每个时刻只需要三个样本来计算能量,这使得TKEO适合应用于故障行波瞬态分量的提取。在本文中,为了便于观察,对TEKO计算得到的瞬时能量进行了归一化处理。

2.3 基于改进CEEMDAN-TKEO算法的故障初始时间提取

基于改进CEEMDAN-TKEO算法提取故障初始时间的流程如下:

1) 采集故障后四个检测端的三相故障暂态电压行波信号。

2) 采用新相模变换,得到故障电压行波信号的线模和零模分量。

3) 使用改进CEEMDAN算法分解对电压行波线模和零模分量进行分解,得到数个由高频到低频的IMF分量。

4) 采用TKEO算法计算IMF1分量的Teager能量值,通过Teager能量谱提取故障初始行波到达检测端的时间。

使用改进CEEMDAN-TKEO算法可以增强故障行波信号的突变特征,减轻数据间的不规律波动,从而实现故障初始时间的精确提取。

3 混合三端线路行波测距方法

3.1 新相模变换

当输电线路发生故障时,由于三相线路之间存在电磁耦合现象,对故障定位产生干扰[20]。为了消除耦合现象,可以采用相模变换进行解耦。传统的相模变换,例如克拉克变换、凯伦贝尔变换,无法用单一的模量涵盖所有的故障类型,需要根据相位配合选择双模量分析,失去了相模变换的意义[21]。文献[22]提出了一种新的相模变换法,用于解耦时可以通过单一模量反映出所有的故障类型。其新相模变换矩阵为

其逆矩阵为:

3.2 故障分支判别

在进行故障定位计算之前,首先需要对故障分支进行判别。

图1为简易的三端架空-电缆混合输电线路模型,F1、F2、F3为3个分支的随机故障点。LAO是架空线路,LBO是电缆线路,LCO是架空-电缆-架空线路,其中OC1段、C2C段是架空线路,C1C2段是电缆线路。

图1 简易三端混合线路模型Fig.1 Simple three-terminal hybrid line model

设故障行波线模和零模分量在架空线路的波速为vol和vo0,故障行波线模和零模分量在电缆线路的波速为vcl和vc0。设LAO的长度为SAO,LBO的长度为SBO,LCO的长度为SCO=SOC1+SC1C2+SC2C。

当O点发生故障时,故障行波线模和零模分量到达各个检测点的时间为

(2)

其中,t1l和t10是行波线模和零模分量到达A端检测点所用时间;t2l和t20是行波线模和零模分量到达B端检测点所用时间;t3l和t30是行波线模和零模分量到达C端检测点所用时间。

根据式(2),可以得到行波线模和零模分量到达各个检测点的时间差:

其中,Δt1是故障初始行波零模和线模分量从O点传播到A端检测点的时间差;Δt2是故障初始行波零模和线模分量从O点传播到B端检测点的时间差;Δt3是故障初始行波零模和线模分量从O点传播到C端检测点的时间差。

当三端混合线路有某处发生故障时,例如F1、F2或F3,假设tAl、tBl、tCl分别为某处故障初始行波线模分量的波头到达A、B、C三端的时间;tA0、tB0、tC0分别为某处故障初始行波零模分量的波头到达A、B、C三端的时间。计算出此时的线模零模分量的时间差:

(3)

其中,ΔtA是故障初始行波零模和线模分量到达A端检测点的时间差;ΔtB是故障初始行波零模和线模分量到达B端检测点的时间差;ΔtC是故障初始行波零模和线模分量到达C端检测点的时间差。

从图1可知,当F1发生故障时,此时故障分支在AO上,此时根据式(3)可以得到三端检测点零模和线模分量的时间差,通过式(4)将其扩展:

(4)

式(4)中,tF1l和tF10分别是故障点F1的行波线模和零模分量到达O端检测点的时间。根据线路参数可知,线模分量波速大于零模分量波速,因而tF1l-tF10是小于零的数。因此当AO区间内发生故障时,可得:

(5)

同理可得,当BO和CO区间内发生故障,根据线模和零模分量时间差,分别具有以下关系,如式(6)和式(7)所示:

(6)

(7)

当故障点发生在O端检测点时,则有:

(8)

因此,当混合三端输电线路发生故障时,根据各个线模和零模分量到达检测点的时间差,结合式(5)—式(8)的判定公式,可以得出故障点所在分支。

3.3 故障路段判别

从图1可知,LCO支路是架空-电缆-架空的混合线路。当LCO支路的F3处发生故障时,传统的定位算法不能直接应用于此,须提前判断出故障点处于架空线路段还是电缆线路段。

(9)

式(9)中tOC1l、tOC10、tC1C2l、tC1C20、tC2Cl和tC2C0分别是故障行波线模和零模分量经过OC1段、C1C2段和C2C段所需时间。

当C1和C2处(电缆和架空线路的连接点)分别发生故障时,故障行波到达C端检测点的零模和线模分量的时间差分别为ΔtC1和ΔtC2,可以根据式(10)计算得出:

(10)

根据式(10)可知,ΔtC1>ΔtC2。

假设LCO支路OC1段发生故障,根据式(4)计算得出的ΔtC,进行如下计算:

ΔtC=tC0-tCl=tC1C20+tC2C0+tF3C10-tC1C2l-tC2Cl-tF3C1=

(tC1C20+tC2C0)-(tC1C2l+tC2Cl)+(tF3C10-tF3C1l)

(11)

其中,tF3C1l和tF3C10是故障行波线模和零模分量从故障点到C1处所用的时间。

根据式(10)和式(11)对比可知,当OC1段发生故障时,ΔtC>ΔtC1。

当C2C段发生故障时,则有:

ΔtC=tC0-tCl=tC2C0-tC2F30-tC2Cl+tC2F3l=(tC2C0-tC2Cl)+

(tC2F3l-tC2F30)

(12)

其中,tC2F3l和tC2F30是故障行波线模和零模分量从故障点到C2处所用的时间。

根据式(10)和式(12)对比可知,当C2C段发生故障时,ΔtC<ΔtC2。

当C1C2段发生故障时,则有:

(13)

根据式(10)和式(13)对比可知,当C1C2段发生故障时,ΔtC2<ΔtC<ΔtC1。

因此,当LCO支路发生故障时,通过C端检测点零模和线模分量的时间差,结合式(10)—式(13),即可判断出故障点所处区间。

3.4 基于线模零模时差的测距算法

文献[23]的基于零模线模时差的行波故障测距算法,具体见式(14):

(14)

式(14)中,v0、vl分别是行波零模和线模的波速;tA0、tAl、tB0、tBl分别行波零模和线模分量到达A端和B端检测点的时间;LAB是A端检测点到B端的距离。

实际应用中无法得到准确的波速值,为消除波速的影响,需对式(14)进行改进。联立方程:

(15)

将式(15)代入式(14),计算得:

(16)

式(16)不受波速的影响,将式(16)引入图1的混合三端输电线路故障定位,当AO区间内发生故障时,可得故障点到O端的距离:

(17)

式(17)中,tO0、tOl分别是故障行波零模和线模分量到达O端的时间。

当BO区间内发生故障:

(18)

当CO区间的OC1区段发生故障:

(19)

当CO区间的C1C2区段发生故障:

(20)

当CO区间的C2C区段发生故障:

(21)

由式(17)—式(21)可知,该测距算法不受波速影响,只需故障行波到达检测点的时间就可以算出精确距离。

4 仿真验证与分析

在Matlab/Simulink中搭建如图1所示的T型110 kV混合输电线路模型。架空线路和电缆线路均采用分布参数模型,架空线路LAO长度为90 km,电缆线路LBO长度为70 km,其中LCO是架空-电缆-架空混合线路,长度分别为60 km、40 km和30 km,总长为130 km。输电线路具体参数如表1所示。

表1 输电线路参数Table 1 Parameters of transmission lines

该系统的仿真时间为0.1 s,采样频率为1 MHz,故障时间是0.035 s,选取故障发生后3 ms的故障分量进行故障定位。下述仿真中,故障距离均指O点到故障点的距离。目前实际情况下,单相接地故障发生概率最高,如若没有特别注释,故障均以单相接地故障为主,过渡电阻为零。

4.1 定位算法对比分析

为了验证本文所提改进CEEMDAN算法的性能,分别通过CEEMDAN和改进CEEMDAN对故障信号进行分解,比较分解结果。

以AO支路为例,在距离O点5 km处发生故障。实验将利用CEEMDAN和改进CEEMDAN对同一故障重复进行十次仿真,结合TKEO提取故障行波到达检测点时间。

为了避免赘述,仅详细给出CEEMDAN-TKEO算法分解其中重复两次的数据,改进CEEMDAN-TKEO算法分解的数据在十次仿真中都是相同的,如图2、图3、图4所示。从图2、图3、图4可知,由于CEEMDAN算法添加了随机的特殊噪声,虽然每次计算得到的IMF分量都有做求均值的处理,但依旧会造成最终提取到的故障时间有一些偏差。

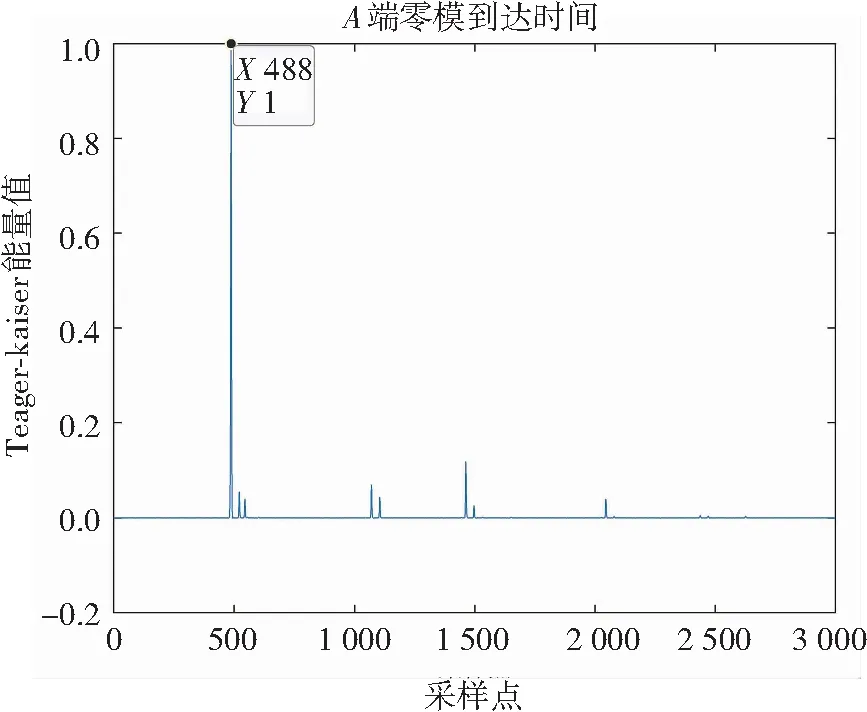
(a) A端零模分量瞬时能量谱

(b) A端线模分量瞬时能量谱

(c) O端零模分量瞬时能量谱

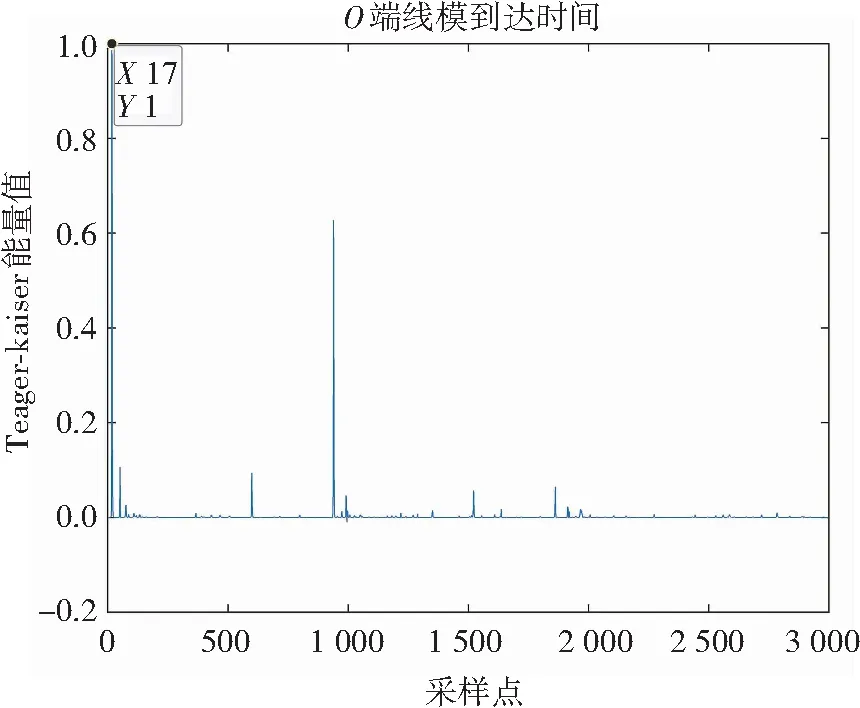
(d) O端线模分量瞬时能量谱图2 使用CEEMDAN的双端瞬时能量谱Fig.2 Two-terminal instantaneous energy spectrum of CEEMDAN

(a) A端零模分量瞬时能量谱

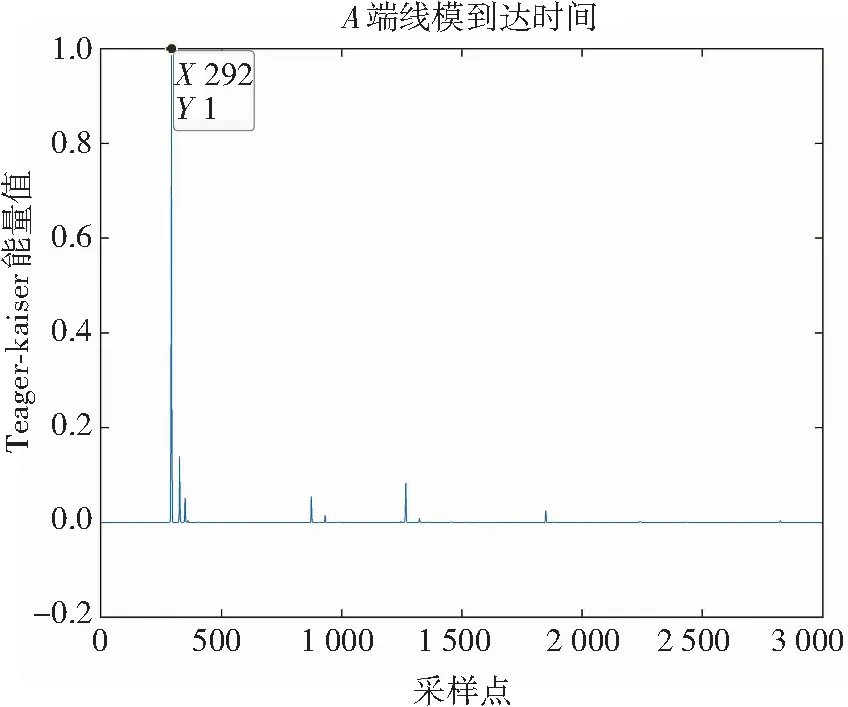
(b) A端线模分量瞬时能量谱

(c) O端零模分量瞬时能量谱

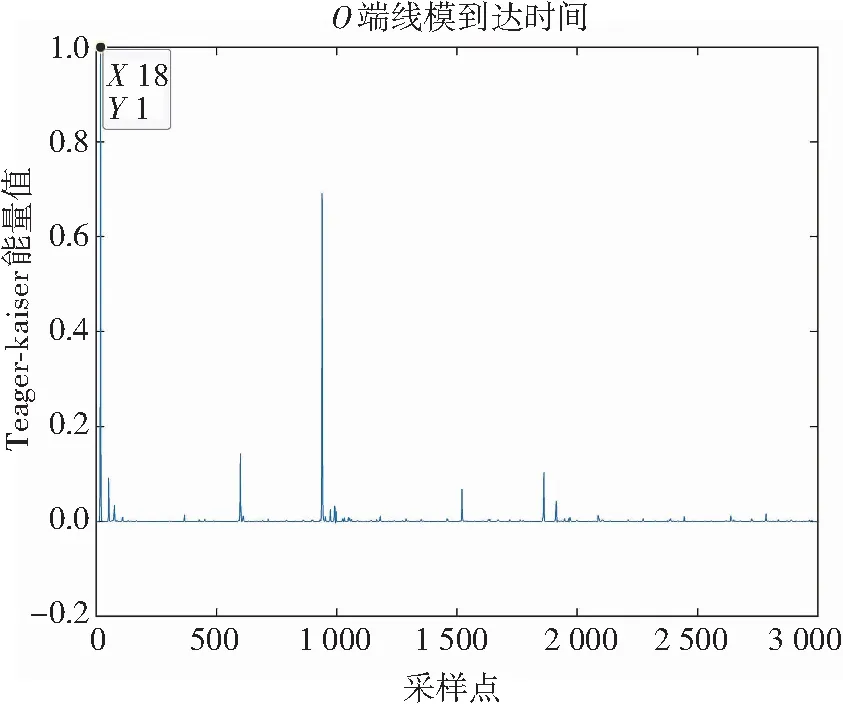
(d) O端线模分量瞬时能量谱图3 使用CEEMDAN的双端瞬时能量谱Fig.3 Two-terminal instantaneous energy spectrum of CEEMDAN

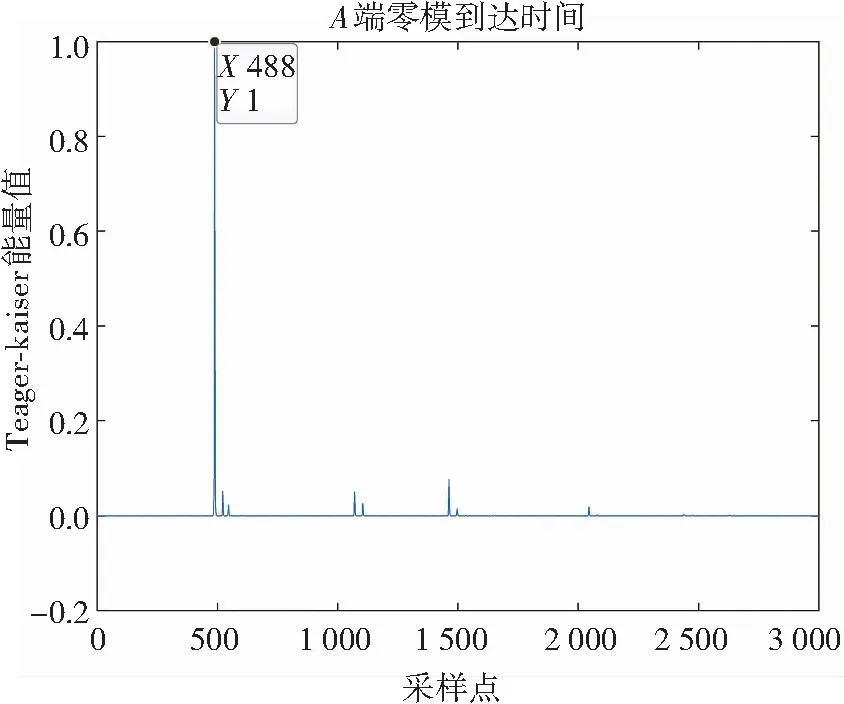
(a) A端零模分量瞬时能量谱

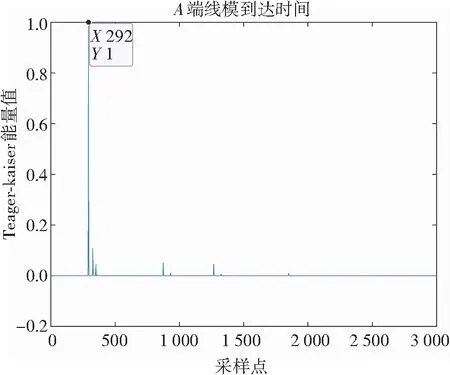
(b) A端线模分量瞬时能量谱

(c) O端零模分量瞬时能量谱

(d) O端线模分量瞬时能量谱图4 使用改进CEEMDAN的双端瞬时能量谱Fig.4 Two-terminal instantaneous energy spectrum of improved CEEMDAN

从图2、图3、图4可得行波线模和零模分量到达各个端点的时间,根据式(17)分别得到故障距离为5.600 km、4.783 km、5.192 km。因此,利用本文所提改进CEEMDAN算法对故障信号进行分解,不仅可以消除随机噪声带来的偏差,而且能提高测距精度。

4.2 故障分支判别分析

由3.2和3.3节可知,通过行波零模和线模分量的时间差,就能得出故障所在分支。为了验证此方法的准确性,在不同支路上的不同距离分别设置故障点,仿真结果如表2和表3所示。

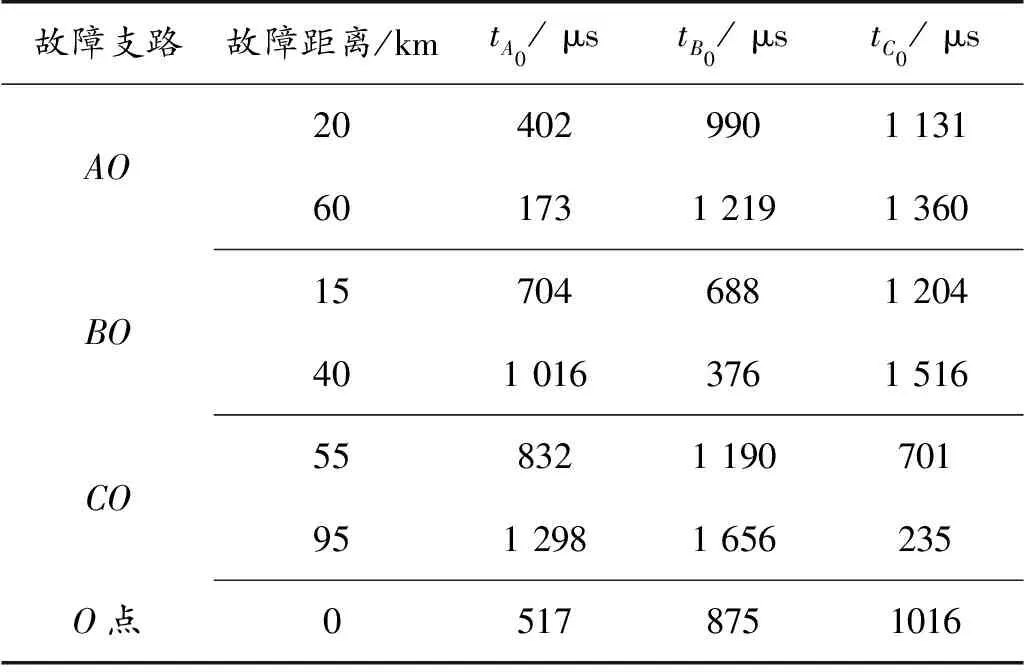
表3 各检测点故障行波零模分量到达时间Table 3 Arrival time of fault traveling wave zero-mode component at each measuring point

从表2和表3可知,所得数据都满足3.2和3.3节的判别公式,可以准确地判断出故障所在支路。

4.3 故障点位置和过渡电阻对故障定位的影响

设置不同的故障点位置和过渡电阻,故障定位仿真结果如表4—表6所示。

表4 AO支路不同故障距离及过渡电阻定位结果Table 4 Location results of different fault distances and transition resistances of AO branch

表5 BO支路不同故障距离及过渡电阻定位结果Table 5 Location results of different fault distances and transition resistances of BO branch

表6 CO支路不同故障距离及过渡电阻定位结果Table 6 Location results of different fault distances and transition resistances of CO branch

从表4—表6可知,本文方法不受过渡电阻的影响,在不同位置的故障点下依旧能准确定位,误差在0.1%以内,可以满足故障定位要求。

4.4 故障类型对故障定位的影响

不同故障类型的故障定位仿真结果如表7所示。从表7可知,本文方法不受故障类型的影响,误差能够控制在0.1%左右。

表7 不同故障类型的定位结果Table 7 Locating results of different fault types

4.5 时间不同步对故障定位的影响

时间不同步对于传统的双端行波测距方法影响较大,目前市面上能接受的时间误差在2 μs。为了验证时间不同步对故障定位的影响,对A、B、C三端检测点分别延时1 μs、2 μs、-2 μs,采用表4—表6部分数据进行仿真验证,结果如表8所示。对比表8和表4—表6的定位结果可知,时间不同步对本文方法不影响。

表8 时间不同步的定位结果Table 8 Locating results of unsynchronized time

5 结 论

针对故障信号在进行CEEMDAN分解后得到的IMF分量出现不规律波动的问题,提出了改进CEEMDAN算法,对IMF分量进行差分运算,可以减少数据的波动,增强数据的突变特征,解决 CEEMDAN算法带来的随机性问题。

针对三端混合线路系统结构复杂以及波阻抗不连续问题,提出了基于零模线模时差的故障分支判别方法。该方法通过三端的零模线模时间差与标准时间差进行对比,确定故障分支线路以及故障所处架空线路或电缆线路,继而利用基于零模线模时差的测距算法得到故障距离。该测距算法不受故障距离、过渡电阻、故障类型、波速的影响,无须对时间同步,兼顾了双端和单端行波测距算法的优点,其中定位误差基本控制在0.1%以内,具有较高精度。

本文所提方法仅在仿真软件上进行试验,有许多理想化的条件。在实际生活中,故障信号会受到周围噪声的干扰。线路的老化、天气的变化等都会影响测距的精度,在实际的工作中,需要考虑各种的外界因素的影响,因此仍需要进行相关研究。