基于KPCA-AGRU神经网络的火电机组NOx排放预测

冯旭刚,文作银,章家岩,张泽辰

安徽工业大学 电气与信息工程学院,安徽 马鞍山 243002

1 引 言

NOx作为火电机组燃烧过程所排出气体的主要污染物之一,极大地影响着生态环境及人类健康[1]。为了防止发电过程中NOx过度排放使得生态环境进一步恶化,我国对其制定了严格的排放标准[2],这使得火电厂在正常生产的同时需控制NOx的排放量。现阶段火电机组降低烟气中NOx浓度以达到烟气排放标准的有效控制技术手段之一为选择性催化还原法(SCR),以低成本、高效率等优点被很多电站采用[3]。这种烟气处理手段的高效性主要依赖对SCR设备入口烟气中NOx的精准实时测量,以改变脱硝过程中的喷氨量。但是电厂现场工况复杂多变,干扰较大,SCR设备入口的NOx浓度频繁多变,这极大影响着SCR的脱硝功效及锅炉燃烧设备。SCR设备入口处NOx预测技术的精准与否对火电机组能否节能减排有着重要的作用[4]。

火电机组NOx排放预测方法是智能发电技术领域的研究难点,有部分学者基于NOx的生成机理和过程进行机理建模。高明明等[5]通过对NOx生成机理分析,以循环流化床锅炉燃烧产生的燃料型NOx为主体,结合应用数学和仿真方案,在以给煤量、风量等作为输入的炉膛出口一氧化碳浓度预测模型的基础上结合即燃碳模型建立了炉膛出口NOx浓度预测模型,仿真表明模型具有较好的精确度;Zhang等[6]通过对增压锅炉的工艺分析对锅炉进行了合理简化,通过炉膛结构、工艺参数搭建炉膛几何模型并利用应用数学知识建立稳态三维湍流模型,完成了锅炉在3种不同负荷下NOx排放的数值模拟。事实上,锅炉燃烧过程中排放的NOx浓度受多种因素影响,且锅炉变量之间存在着强耦合,很难通过机理建模建立满足现代工业生产所需求的准确性及可靠性。

相较于机理建模,现技术成熟的数据建模因不需太关注系统内部结构及良好的非线性拟合能力等优点被大量地使用。郭建民等[7]利用火焰诊断系统对炉膛温度场进行多次测量以研究温度与NOx生成机理的关联,应用支持向量机(SVM)模型通过两者间的关联建立了锅炉NOx排放特性模型;Ahmed等[8]在之前研究最小二乘支持向量机(LSSVM) NOx排放预测模型的基础上融入实时更新技术建立实时NOx排放预测模型,实验结果表明新方案在较长时间内的鲁棒性预测具有更高的准确度;Lyu等[9]提出软模糊c均值聚类算法,对原始数据进行分解并应用偏最小二乘(PLS)消除模型的冗余变量,建立最小二乘支持向量机(LSSVM) NOx排放预测模型。人工神经网络(ANN)是另一种对非线性函数有良好拟合能力的人工智能技术。Wang等[10]采用主成分分析(PCA)处理原始数据,消除冗余变量建立以遗传算法优化网络参数的BP神经网络,实验表明PCA降低了NOx预测模型的复杂度,提高了精准度。以上研究虽有良好的NOx预测效果,但锅炉NOx的产生是由锅炉之前的状态和锅炉各变量此时的输入混合作用而成,上述建模方法难以反映变量数据之间存在着时序联系。

综上所述,考虑NOx排放所具备的非线性和时序性等特点,本文提出一种基于核主成分分析(KPCA)和注意力机制(AM)的门控循环(GRU)神经网络NOx排放预测模型。采用核主成分分析法对采集到的变量数据进行冗余变量去除处理;引入注意力机制,突出与输出变量有强相关因素的影响,降低弱相关因素的影响,实现深层次关键信息的挖掘,提高预测效果,且针对GRU神经网络超参数手动调参的困难,采用网格搜索对其寻优,加快网络的学习效率,提高模型的准确性。

2 门控循环神经网络

循环神经网络(RNN)对时间序列具备强大的特征表征和映射能力,能够有效处理变量数据之间存在的时序联系,其建立的模型也更为精确。然而RNN存在着梯度消失和梯度爆炸的问题,这使得模型无法正常训练[11]。长短期记忆(LSTM)神经网络引入门单元,改进了RNN模型的结构,通过时序记忆可控的能力弥补了RNN模型的缺陷,并在火电机组NOx的排放预测中具备了良好的预测效果[12]。而GRU神经网络是对LSTM神经网络结构进一步改进所得到的产物。

GRU内部结构如图1所示:rt与zt分别是GRU的更新门和重置门,其阈值区间为[0,1]。由图1可知:此时的门控状态信息是由上一时刻的状态与当前时刻输入决定的。相比于采用3个门单元(输入门、遗忘门和输出门)控制输入输出的LSTM神经网络,GRU只存在两个单元门(更新门和重置门),这在继承LSTM神经网络有效处理时序序列能力的同时简化了模型结构,缩减了网络的训练参数,提高了网络计算效率。这使得GRU神经网络具有更好的时序序列处理能力。而火电机组的NOx排放预测需要注意NOx浓度数据的时间相关性。使用GRU神经网络可以充分地利用样本数据中的时序特征,以达到更好的预测效果。

图1 GRU内部结构图Fig.1 Internal structure of GRU

GRU单个隐含层传播过程如下:

(1) 更新门zt逻辑为门控制状态,它的作用是处理上一时刻隐含层输出ht-1和当前时刻输入样本xt。

zt=σ(xtWxz+ht-1Whz+bz)

(1)

(2) 同理,重置门rt逻辑为门控制状态,作用也是处理上一时刻隐含层输出ht-1和当前时刻输入样本xt。

rt=σ(xtWxr+ht-1Whr+br)

(2)

(3)

(4) 当前隐含层输出ht由更新门对上个时刻隐含层输出和当前时刻节点即时信息的选择和遗忘得到。

(4)

3 氮氧化物预测模型构建

3.1 核主成分分析

输入变量的筛选在数据建模中极大地影响着模型的质量。火电机组燃烧过程中产生的NOx与锅炉的众多参数有关,如果将其相关变量都作为模型的输入变量会使模型引入冗余信息,降低模型的质量和预测精度。

KPCA利用核函数映射低维空间数据,当这些数据转换至高维空间后再利用PCA对数据进行简约处理。与传统的PCA相比,经过KPCA处理的数据保留了原始数据的非线性特征,弥补了PCA算法处理非线性数据方面的劣势[13]。

设原始数据集构成原始空间为Rn,输入数据为X,X有m个样本,每个样本具有n维数据。故X=[x1,x2,…,xm],xi=[xi1,xi2,…,xin],i=1,2,…,m。设H为高维特征空间,设定Φ为原始空间数据到高维空间的非线性映射,则任意xi通过映射至高维空间中为

xi→Φ(xi)

(5)

在映射完成后,H空间中映射数据的协方差矩阵CH可表示为

(6)

求解CH的特征值λ和特征向量VH,即

λVH=CHVH

(7)

其中,特征值λ≥0,特征向量VH∈H≠{0}。则有

λ(Φ(xk)VH)=Φ(xk)CHVH

(8)

非零特征值λ对应的特征向量VH是由{Φ(x1),Φ(x2),…,Φ(xm)}张成的空间,则VH可由其线性表示为

(9)

将式(6)、式(8)与式(9)联合整理后得到

(10)

引入核函数k(xi,xj)=Φ(xi)TΦ(xj),本文采用高斯核函数分析,如式(11)所示;核矩阵为K=[k(xi,xj)]m×m。对式(10)进行化简整理可得式(12):

(11)

mλα=Kα

(12)

由此可得K矩阵的特征值与特征向量。

上式中的K矩阵是经过中心化处理的。中心化的计算如式(13):

K-ImK-KIm+ImKIm→K

(13)

K的特征值λ1≥λ2≥…≥λm,其中特征值λi的累计贡献率ηi计算公式为

(14)

依据各主成分贡献率和累计贡献率,设定累计贡献率阈值从而确定数据的主成分和模型的输入变量。

3.2 注意力机制

注意力学习机制是对人脑注意力的仿生,其核心思想是人脑会对重要信息分配更多的注意力,以获得更多的重要信息[14]。AM在模型中的体现是通过模型自主学习出一组权重系数并将其赋予输入数据,以此来突出对结果影响较大的输入,忽略无关信息。本文引入AM,给予输入特征不同权重,突出与NOx浓度相关性较大的输入特征,弱化相关性较小的输入特征来提高模型精度与计算效率。AM结构如图2所示。

图2中,x1,x2,…,xn-1,xn为输入数据;h1,h2,…,hn-1,hn为某一时刻输入数据的状态值。AM的运算步骤主要如下:采用注意力打分函数对将要输入至AM的输入特征进行打分计算;然后利用打分计算结果得到注意力分布,即为权重系数;将不同的权重系数分配给输入特征进行乘积求和得到最终结果。

其计算公式如下:

Scor(et)=vtanh(wht+b)

(15)

(16)

(17)

图2 注意力机制结构图Fig.2 Structure of attention mechanism

式(15)—式(17)中:Scor(et)为注意力打分函数;at为注意力权重;v、w、b分别是计算注意力权重时的多层感知机的权重与偏置参数;ht是隐藏层状态;C是AM加权求和后的输出。

3.3 网络训练

批量梯度下降(BGD)、随机梯度下降(SGD)和小批量梯度下降(MBGD)是常见的网络训练方式,但这3种方法在训练中各有特点[15]。在迭代过程中,BGD需要对所有样本的梯度和权重进行重新计算,这严重拖累了训练过程。SGD通过随机选定一个样本来更新权重参数,这样的随机性会导致样本存在大量噪声。MBGD通过将输入样本小批量化来计算梯度和相应权重参数,从而降低计算量。小批量梯度下降法是本研究采用的训练方式。网络以均方误差(FMSE)为损失函数,其计算公式如式(18):

(18)

采用自适应动量估计(Adam)来优化训练中的学习率,Adam结合了动量法与RMSprop算法的优点,在迭代过程中不仅可以使用动量作为参数更新方向,而且可以自适应调整学习率,提高参数优化精度。Adam的迭代过程如式(19):

(19)

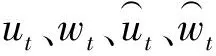
3.4 模型构建

将工业现场采集的原始数据经过数据预处理后先进行核主成分分析,消除冗余变量,然后将其划分数据集,利用训练集训练GRU神经网络,并采用网格搜索对GRU神经网络超参数进行寻优。同时,运用Adam算法对网络内部参数进行优化,最后引入注意力机制计算权值,实现区分输入特征处理,从而建立NOx排放预测模型。图3是基于核主成分分析和注意力机制的门控循环神经网络NOx预测模型。

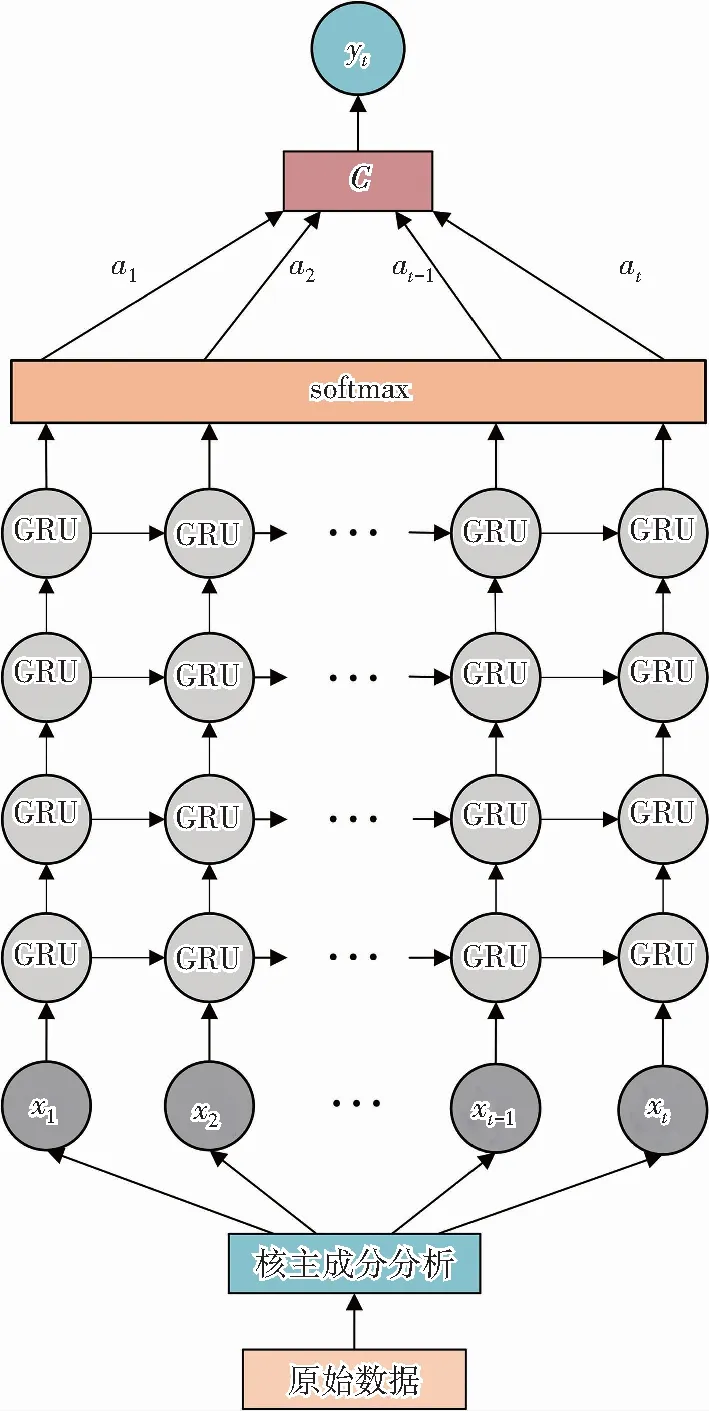
图3 KPCA-AGRU NOx预测模型Fig.3 NOx prediction model based on KPCA-AGRU

4 实验设计与结果分析

实验采用Intel Core i5 12400处理器、32G内存,GPU选用NVDIA RTX2060 12G显卡,操作系统为Windows系统,开发语言是Anaconda集成环境中的Python3.8编写实验代码,开发工具为PyCharm Community Edition。

4.1 输入变量选择

建模数据来自某燃煤电厂330 MW机组DCS系统,锅炉负荷在300 MW上下浮动,采样周期为300 s。燃煤机组工作过程中生产的氮氧化物主要由燃料型、热力型和快速型3种组成。快速型NOx在锅炉正常运行时含量较小可忽略不计,燃料型和热力型NOx为锅炉燃烧产生NOx的主要成分,并且其产生与多种锅炉参数有关[16]。依据氮氧化物生成机理与电厂现场运行工况,初步选定20种参数作为模型的输入变量,分别为锅炉负荷(1组)、烟气含氧量(2组)、空气预热器入口烟温(2组)、给煤量(5组)、一次风量(5组)、一次风温(5组)。

将采集到的变量参数进行数据预处理。首先采用拉以达准则对各参量数据中的异常值进行剔除;接着使用线性插值法按照时间标签对数据中的缺失值和去除的异常值空位进行补位;最后将数据归一化至[0,1]。

选定的变量之间存在着较强的相关性,直接作为模型输入会产生维数灾难。KPCA在保留数据非线性特性的同时消除了冗余变量,减少了输入维数,降低了模型复杂度。对所有输入变量进行编号后经过核主成分分析的结果如图4所示。由图4可知:前9种成分的累计贡献率已达到95.15%,这表示这9种成分已包含原始数据95%的信息,故摒弃其他成分,只选取这9种主成分作为模型的输入。

图4 核主成分分析结果Fig.4 Results of kernel principal component analysis

4.2 参数设置

4.2.1 网络初始化

采集数据有2 000组,训练集与测试集划分比例为8∶2,建立4层GRU神经网络,采用MBGD和训练网络,通过Adam优化学习率。

根据实验和参数设定经验,初步确定模型的初始参数:批量大小为64,时间序列长度为5,学习率为0.01,四层隐含层神经元个数分别为[128,128,64,32],训练总次数为500。

4.2.2 超参数调整

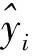
(20)

(21)

表1 GRU网络模型时间序列长度选择对比Table 1 Comparison of time step selection of GRU network model

由表1所示:随着时间步长的增加,模型的精度在总体上得到提升,当时间步长为32时,所得的FRMSE、FMAE最小,网络的预测效果最好。但是当时间步长持续增加时,模型的预测精度在降低。这为下一步GRU的超参数调试做好了准备。

在时间步长得到最优后,为了进一步提高网络模型的预测精度和拟合效果,采用网格搜索对网络的隐含层单元数、批量大小、学习率进行寻优。隐含层单元数的寻优范围为[16,32,64,128,256],批量大小范围为[16,32,64,128,256],学习率寻优范围为[0.01,0.001,0.0001]。参数网格搜索的步骤:初步确定隐含层单元数、批量大小、学习率的选取范围;计算网络模型预测精度;比较不同参数网络的预测精度并选择使网络预测精度达到最大值的参数。经参数寻优后,当各隐含层单元数为[64,128,64,256]、批量大小为16、学习率为0.01时,其均方根误差和平均绝对误差最小,模型的预测精度最好(FRMSE值为3.332 mg·m-3,FMAE值为3.022 mg·m-3)。

4.3 模型预测结果

采用网格搜索对GRU神经网络的超参数进行寻优后,引入注意力机制对经过GRU处理后的信息进行深度挖掘,提高模型的精准度。为了验证KPCA-AGRU网络模型在火电机组SCR系统入口NOx浓度的预测效果,本节在同样输入变量基础上,将AGRU预测模型、GRU预测模型和传统BP神经网络预测模型的测试集预测结果进行对比。这3种NOx预测模型针对测试集的结果见图5。可以看到:融入了AM的GRU模型相比于另外两种模型有着更好的跟随趋势变化能力,尤其在NOx变化幅度较大时,有着更好的预测效果。3种预测模型的评价指标对比见表2。由表2可知:AGRU相比于BP预测模型,其FRMSE值降低了62.79%,FMAPE值降低了63.20%;相比于GRU预测模型,其FRMSE值降低了37.36%,FMAPE值降低了34.14%。对比结果表明:GRU神经网络对时序序列具有较好的处理能力,并且引入注意力机制可以有效减小GRU神经网络预测模型的预测误差,提高整体模型的准确性。

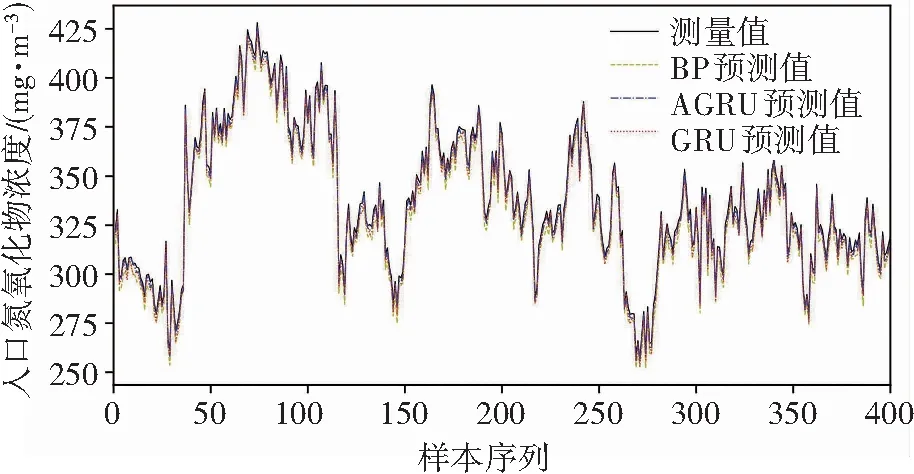
图5 3种模型预测结果Fig.5 Prediction results of three models

表2 不同模型的预测精度Table 2 Prediction accuracy of different models

5 结 论

利用对时序数据有良好处理能力的GRU神经网络建立火电机组氮氧化物排放预测模型有着不错的预测效果。但是使用原始数据直接建模会发现输入维数过高,此外网络处理的结果没有很好地体现对输出变量有较大贡献的输入特征的作用。针对这两点不足,利用KPCA降低模型维数,引入注意力机制增强不同信息的敏感度,突出对输出贡献较高的输入特征,提高模型预测精度。某330 MW机组运行数据对比实验表明:AGRU预测模型的均方根误差和平均绝对误差较BP和GRU模型小,可较为准确地预测NOx浓度。在后续的研究中,可在本研究的基础上探究集成算法在锅炉 NOx浓度预测上的有效性。