Resource Trading and Miner Competition in Wireless Blockchain Networks with Edge Computing

Yuchen Zhou,Jian Chen,Lu Lyu,Bingtao He

The State Key Laboratory of Integrated Service Networks,Xidian University,Xi’an 710071,China

*The corresponding author,email: jianchen@mail.xidian.edu.cn

Abstract: To promote the application of edge computing in wireless blockchain networks,this paper presents a business ecosystem,where edge computing is introduced to assist blockchain users in implementing the mining process.This paper exploits resource trading and miner competition to enable secure and efficient transactions in the presented business ecosystem.The resource trading problem is formulated as a Stackelberg game between miner candidates and edge computing servers,where computing,caching,and communication resources are jointly optimized to maximize the potential profit.Partial offloading is introduced to further enhance the system performance when compared with the existing work.We analyze the existence and uniqueness of the Nash equilibrium and Stackelberg equilibrium.Based on the optimization result,winners are selected from the set of miner candidates by bidding and constitute the mining network.Simulation results demonstrate that the proposal is able to improve the social welfare of blockchain miners,thus stimulating more blockchain users to join the mining network.

Keywords: blockchain;edge computing;miner competition;resource trading;social welfare

I.INTRODUCTION

Recent years have witnessed the rapid development of blockchain technology(BCT),along with lots of great work to exploit the application of BCT [1,2].Essentially,BCT is a Peer-to-Peer(P2P)network,where transactions are recorded in an entirely decentralized,secure,and transparent manner,and any node in the network can participate in transaction recording and block building.When a node is chosen as the miner,it is expected to have some computation ability to generate new and valid blocks by a specific hash function.However,most of the nodes,such as user devices,have limited computation resources to implement such a mining process.Under this background,edge computing technology is introduced to assist the node with limited computation capability by offloading mining tasks to an adjacent computing server instead of relying on a remote cloud[3,4].Therefore,the application of edge computing to wireless blockchain networks attracts great interest from both academia and industry.

The authors in [5] deploy a real mobile blockchain mining experimental environment with Ethereum to demonstrate that the probability of successful mining is improved by edge computing servers.In [6],edge computing is taken as an effective solution for blockchain-based cloud-industrial Internet-of-Things(IoT) to enhance the capabilities of cloud computing and reduce the risk of disclosing raw data of terminal devices.The authors in [7] point out that for blockchain-enabled healthcare IoT,edge computing enables a faster response with efficient usage of bandwidth and power,and it can also optimize the network performance and ensure network security.In addition,edge computing is able to assist blockchain nodes in offering name resolution and edge authentication service [8],which can be widely used in existing intelligent applications (such as smart city,smart home,smart factory,and public security)[8].

With the increase of access devices and network data volume,resource management for wireless blockchain networks with edge computing has become an emerging technology.Most existing studies focus on resource optimization for users in edge computing systems,where blockchain is only used to provide the data management function [9,10].The authors in[11]further propose an adaptive resource allocation and block generation scheme to guarantee the performance of both the overlaid blockchain system and the underlaid edge computing system,where only edge computing servers are utilized as blockchain miners.In edge computing-enabled wireless blockchain networks,users can be viewed as blockchain miners as well as blockchain clients [12].The authors in [12]and[13]propose the computation resource allocation and pricing scheme for users as blockchain miners.To further promote the mining process,the authors in[14]propose that the mining task can be offloaded not only to edge clouds but also to neighbor idle devices.However,these studies focus on maximizing the potential profits of miners or edge servers without the consideration of the limitation of computation capability at edge servers.Besides,these studies aim at computation optimization for edge servers,and the network dynamic nature and communication optimization are not well studied.

This paper focuses on resource trading and miner competition for edge computing-enabled wireless blockchain networks.We maximize the social welfare of miners to stimulate blockchain users to join in the mining process by exploiting multi-resource optimization,resource pricing,and miner competition.Different from the existing work,the joint optimization of computing,caching,and communications is introduced to further promote the mining process [15].Furthermore,with the consideration of the computation capability limitation,partial offloading will be investigated to provide a more flexible solution on the basis of a higher resource utilization compared with local computing and binary offloading.

Specifically,the study we present in this paper poses two challenges as follows:

·Optimization correlation and complexity: Even though edge computing servers and miners determine the resource pricing and resource demands respectively,there exists an optimization correlation between them.The resource demands of miners influence the pricing strategy of the edge computing server,and meanwhile,the pricing strategy of the edge computing server also influences the resource demands of miners.It is necessary to achieve an equilibrium since both of them may want to obtain a higher potential profit.In addition,the introduction of partial offloading increases the problem complexity and makes it hard to verify the uniqueness of game equilibrium.

·Information non-transparency: Since the wireless blockchain network is entirely decentralized,each miner determines the resource demand without the knowledge of others.Besides,in order to join in miner competition,bidding prices given by miners are also based on their individual resource demands without the prior knowledge of the number of winning miners and the resource demands of others.This will also result in difficulties in problem construction and solution.

The distinctive features of this paper are as follows:

·Resource demand and pricing: Since the bidding price is usually based on the number of consumed resources,we first need to determine the resource demands of miner candidates and the resource pricing of edge computing servers.The problem is formulated as a Stackelberg game to maximize potential profit.The Nash equilibrium and Stackelberg equilibrium of the game are verified to be existed and unique.The analysis shows that each miner candidate can decide their resource demands independently.

·Miner competition: Based on the resource demands,a network effect function is introduced to achieve independent bidding during miner competition.To efficiently solve the miner competition problem,we define the individual additional contribution value for each miner when it joins the mining network,and the miners are selected according to the ranking of the defined value.We also verify the convergence of the proposal.The simulation results verify the performance advantages of the proposal.

The rest of this paper is organized as follows.In Section II,we exploit resource trading and miner competition for wireless blockchain networks with edge computing.In Section III,the performance of the proposal is validated via simulations.Finally,we conclude our study in Section IV.

II.RESOURCE TRADING AND MINER COMPETITION

This section presents the scheme of resource trading and miner competition for wireless blockchain networks with edge computing.

2.1 Business Ecosystem

Figure 1 illustrates the business ecosystem for wireless blockchain networks that allow transactions among entities in a verifiable and permanent manner.To overcome the shortcoming of limited resources,edge computing servers are used to assist in implementing the mining process.Users can act as miners or blockchain clients,or both of them.The difference between these two characters is whether they join in the mining process.The client only generates transactions,and the consensus process is implemented by miners.To become a miner,each user can compete with each other,and the winners will constitute a miner network.The miner network matches the transaction pairs and obtains the authority to update and verify the distributed ledger with transaction details,such as timestamp,ownership,and price [16].All transactions during a period of time need to be linked together and stored into a new block by the miner network.The generated new block will be broadcast in the miner network and verified by each miner.They decide together whether to accept the new block through the longestchain rule.The collusive mining strategy is adopted,where the winners mine collaboratively and share the reward once successfully mining a valid block[12].

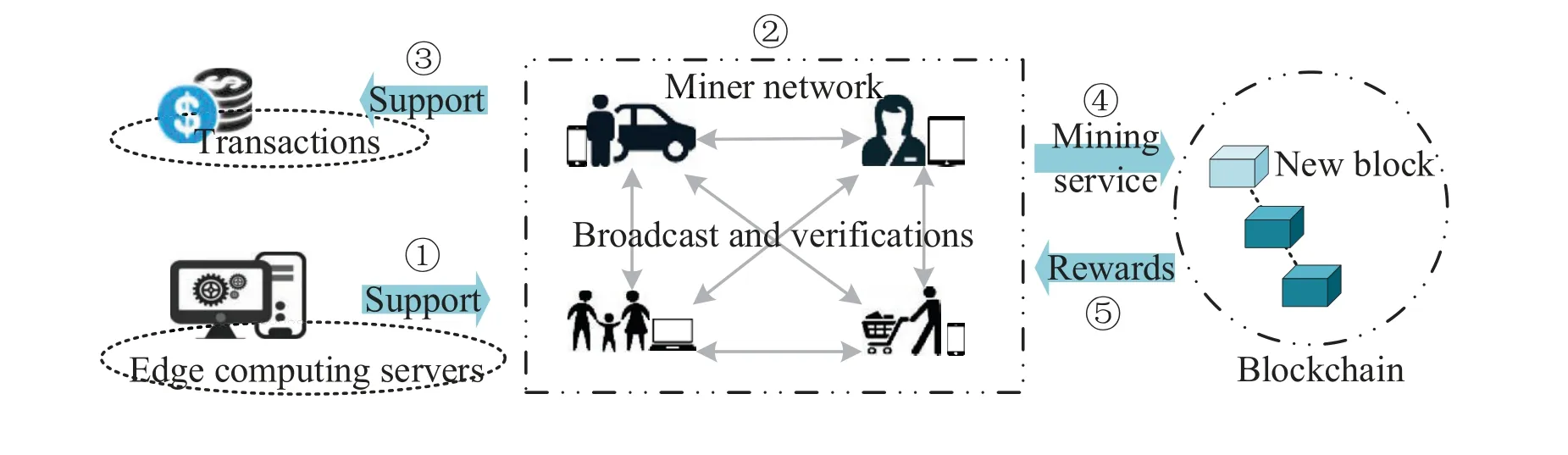
Figure 1. Business ecosystem.

Under this background,if a tampered block is generated by a malicious node,it needs to successfully deceive at least 51% of the miners in order for the tampered block to be accepted.To avoid this severe scenario,we allow the maximum number of users to join the mining network to maximize social welfare under the premise of limited network resources,and strict hashing is adopted.The hash function is a oneway function so that it is easy to be verified but hard to inversely deduce the inputs.As a result,it is almost impossible for malicious nodes to break through the security of blockchain systems.Another suggested approach is to change the rights of miners randomly and ensure that no user can act as miners continuously[7].

2.2 System Model

In this paper,we use a set M={1,2,...,m,...,M}to denote miner candidates,and the set M′ ∈M denotes the winners after the miner competition.Denote E={1,2,...,e,...,E}as the set of edge computing servers.We assume that the proposed framework is based on the classical Proof-of-Work consensus protocol[17],and the resources of miners may be limited for building blocks.In general,edge computing servers can be installed at base stations or access points [18].Therefore,we assume that the selected miners can rent resources from the edge computing servers,including communication bandwidth,computation workload,and caching space.

To compete,each miner candidate needs to give a bidding price.The price is usually based on the estimated value of the consumed resource during the mining process.Therefore,each miner candidate and edge computing servers first predetermine the required resource number and the resource pricing for maximizing their potential profits.Afterward,the winners are selected through bidding,and they make payment and access the edge computing servers to execute the mining process.Once successfully mined a valid block,the miners will share the reward to stimulate them to continue to work for the system and regulate behaviors[19].

2.2.1 Computation and Caching Model

Assume that miners can rent computation resources from edge servers,and the computation consumption of block verification is ignored in this paper.The computation ability of the minermincludes the selfcomputation abilityand rent-computation ability.Here,the computation ability is quantized by the number of CPU cycles per second.After the verification,the valid block needs to be cached at each miner.Since the storage space at each miner is limited,assume that each miner can store a partial blockchain ledger,such as the latest several blocks,and the others are stored at the edge computing servers in a distributed manner[20].The caching space of each miner includes self-cache sizeand rent-cache size.

2.2.2 Communication Model

The miners need to upload the mining task to the edge computing server so that the server can help generate a new valid block.The server can also be used to help with block propagation across the mining network.This paper focuses on the uplink transmission from each miner to its serving base station or access point.The performance analysis and optimization of the downlink broadcast can be performed in a similar manner.

We assume that each miner is associated with its nearest edge computing server [21],and Merepresents the set of miners associated with the servere.The miners need to be assigned enough spectrum to guarantee their communication rates.Assume thatbmis the spectrum resource blocks required by the minermto upload the mining task.The path loss between the minermand its associated edge computing server isg(dm)=,wheredmrepresents the communication distance,Γ is a constant of the path loss,andαis the path loss exponent [21].Meanwhile,the Rayleigh fading is denoted ashmfollowing the exponential distribution with the mean 1/μ.The signal to interference plus noise ratio (SINR)SNRm(hm,dm) can be calculated asSNRm(hm,dm)=Pmhmg(dm)/(σ2+I),where we usePmto represent the transmission power.The additive white Gaussian noise at base stations obeys the independent identical distribution with the mean of 0 and the variance ofσ2,andIdenotes the received interference from the miners associated with other servers[22].

Assume that miner devices and edge computing servers are geographically distributed as the homogeneous Poisson point process with density parametersλdandλb.In this paper,we suppose that each miner connects to the nearest server;thus we need to consider what if it’s not covered.The miner candidates beyond the base station coverage will generate an outage,and thus it cannot be chosen as the winner while miner competition.Once the miner device is located within the coverage,it can adjust its transmission powerPmto guarantee the SINR threshold.Under this background,we first need to derive the probability density function(PDF)of the distancedmbetween the minermand its server.

Proposition 1.The PDF of dm can be calculated as.

Proof.For convenience,Dis used to represent the distance threshold.Note thatdm ＞Drepresents that there is no server for the minerm.Thus,the outage probability can be derived as Pr(dm ＞D)=,and the PDF ofdmis(D)=∂(Pr(dm ≤D))/∂D=∂(1-Pr(dm ＞ D))/∂D=2×.

Proposition 2.Based on Proposition 1,if we further consider the effect of Rayleigh fading on the achievable SINR,the average spectrum efficiency (SE) can be calculated as(1)according to the stochastic geom-etry method.

Here,we assume that the covering radius of each edge computing server is Dth,and the minimum distance between the miner m and its server is Dm.

Proof.The average spectrum efficiency is taken over the fading distribution including the path loss and Rayleigh fading;thus

Therefore,the achievable average communication rate of each minermcan be calculated asRm=bmSEm.

2.2.3 Miner Reward

According to the current researches,we define two kinds of rewards[12,13,19]:

Definition 1.The expected mining reward is an ideal reward that is defined as(3)[12,13].

Here,Qandqrespectively represent the fixed reward and average mining reward for each transaction.Since the collusive mining strategy is adopted,the transaction numberTmfor each miner is equal[12].Pvm=is the possibility to generate a valid block by the minerm,whereλ=1/600 represents the mean value of the Poisson distribution[23],andt=0.005 reflects the impact of the transaction numberTmon the block propagation and verification [12,24].According to [12],define Pnm=as the contribution parameter to enable the reward sharing,which can also be viewed as the probability of successful mining for the minerm.

Definition 2.The actual mining reward defined as(4)is the final reward after successfully mining a valid block.

Different from(3),it further contains a positive feedback function to evaluate the network utility generated by the minerm[19].Here,N(φ) is the network effect function to calculate the value conversion of the miner with the invoked computing resourcerepresents the normalized invoked computing resource of the whole system,andYrepresents the maximum quantity of the computing resource owned by the system and miners.In this paper,we define the network effect function asN(φ)=a1φ-∈[0,1],wherea1,a2,anda3are positive parameters [19].From (4),one can observe that the partis only related to the minerm.Therefore,we define the bidding price Mbmas

This bidding price is given on the assumption that the minermcan generate a valid block.To share the reward,the final payment is the bidding price multiplied by a loss rate that contains two parts: the contribution parameter Pnmand the achievable network effectN(φ).

2.3 Resource Demand and Pricing

According to (5),the bidding price is based on the consumed resource number during the mining process.Therefore,before selecting winners from miner candidates(i.e.,miner competition),it is necessary to determine the miner candidate’s demands for various kinds of resources and the resource pricing of edge computing servers.

2.3.1 Problem Formulation

(1)Miners’ sub-game: Miners’ sub-game is formulated as OP1 to maximize the potential profit of each candidate.

Here,the constraint restricts the minimum computation,caching,and communication requirements,i.e.,,and.ηis the proportionality constant that represents the equivalent price per unit throughput,and{c1,c2,c3}represents the unit cost for each miner to obtain computation,caching,and communication resources.Specifically,the three terms in the objective function can be respectively explained as follows: i) The first term represents the expected reward of each miner candidate before selecting as the winner;ii)The second term indicates the price equivalent of throughput Thmthat is defined as Thm=ln(Rm) +ξ,whereξis a constant [25];iii) The third term indicates the payment to obtain computation,caching and communication resources if it is chosen as the winner.

During resource optimization,the required resource number of each miner candidate is unclear so that the bidding price is still unknown.It is also unclear how many winners will be chosen after the miner competition.Therefore,the expected miner reward is used in the most competitive situation,where all the miner candidates are assumed to be selected as winners.

(2)Servers’ sub-game: Edge computing servers’sub-game is also formulated to maximize its potential profit in OP2.

Here,we assume that uniform pricing for each kind of resource is given for all servers.are the unit cost to provide the resources.Here,we assume the unit pricec{·}is actually composed of the foundation unit pricec0{·}and the floating unit pricei.e.,c{·}=c0{·}+.The former is assumed to be known and used to ensure the basic profitability of the servers.The latter is used to increase the profit margin that is also the key optimization in OP2.

2.3.2 Problem Analysis and Optimization

(1)Miners’ sub-game: Given,each candidate competes to maximize its profit.Denote the optimal solution of the miner candidatemas ˆSm=,and letbe the optimal solutions of other candidates.

Proposition 3.The Nash equilibrium of OP1 exists.

Proof.Obviously,the objective function is linear with,and the strategy space of OP1 is a convex,continuous,and nonempty subset of the Euclidean space.As forandbm,the first and second derivatives are

It proves that the Nash equilibrium exists in OP1.

Proposition 4.The best response function of the miner candidate m,i.e.,,is given by(10).

Proof.From=0,and∂ωm/∂bm=0,we have

Therefore,the optimal solutionis obtained as(10),whereindicates that ifx ＞xmax,we set it to its upper limitxmax.Note that in a decentralized blockchain network,each miner candidate decides the required resource number without knowing others’requirements.However,as shown in (11),the required computation ability of the minermis related to the requirements of other miners.Therefore,to be clarified,we further derive an optimal closed-form expression of.

Proposition 5.The closed-form expression ofcan be further clarified as

where the sum ofcan be viewed as a global known quantity without knowing Am of each miner.

(2)Servers’ sub-game: Obviously,the objective function is linear with.As forand,we have the following propositions:

Proposition 6.If none of the optimal solutions to OP1 violates the constraints,the Nash equilibrium of OP2 exists.

Proof.The first and second derivatives ofare

and

whereIt is obvious that OP2 is convex with.Therefore,the Nash equilibrium exists,which can be derived from=0,and the closed-form expression is

As for,substituting(12)into the objective function in OP2,we will find that the optimal solution ofcan be determined as its upper limit.

Proposition 7.If only some of the optimal solutions to OP1 violate the constraints,the Nash equilibrium exists when＞0,where Cm=.

Proof.Denote M1and M-1as the miner set whose values of(13)satisfy and violate the constraint in OP1,respectively.The first and second derivatives ofcan be derived as

It is obvious that the Nash equilibrium exists in the second case only whenC(1-CCm)＞0.In this case,the Nash equilibrium can be derived from=0,and we have

Third,we prove the scalability.We have(22).

2.4 Miner Competition

After specifying the demand and pricing,the bidding prices can be determined.The focus of the problem shifts to the miner competition.

2.4.1 Problem Formulation

The optimization problem of miner selection is formulated as OP3 to maximize the social welfare of miners.The constraint restricts that the allocated resources cannot exceed the total resource number at each edge computing servere.During miner competition,the required resource number of each miner candidate is already known by the associated edge computing server,and(4)can be used to calculate the value conversion,which can also be viewed as the final reward to the winners if the generated block is verified.Under this background,jointly considering the income and expense,the objective function in OP3 can be defined to indicate social welfare after the miner competition.

2.4.2 Problem Analysis and Optimization

Definition 3.The individual additional contribution value is defined as

which is the social welfare contribution of the miner candidate m if it joins in the winner set.

According to the definition,all the miner candidates are sorted in non-increasing order,and we find the set of winnerscontainingLminers that satisfy≥0 and＜0.Then,the optimal solution of M′is.Note that while determining the winner set,we need to guarantee that the allocated resources cannot exceed the total number of the resources owned by each edge computing server.To prove the convergence,we have the following propo-

sition.

Proposition 9.The function S(M)is submodular,andthe proposal can be efficiently converged.Proof.AssumeSn(M)is defined as(24).

To prove that the functionS(M) in OP3 is submodular is equal to prove thatSn(M) is monotonically decreasing [26].It is apparent that if we expand M,the second term of (24) is monotonically decreasing.Note that while expanding M,is negative and decreasing,and the termis positive and increasing.Therefore,the first term of(24)is also monotonically decreasing.Now,we have proved that the functionS(M) in OP3 is submodular.IfS(M) is submodular,expanding M,Sm′(M′)will be monotonically decreasing,and thus the proposal can be efficiently converged.

2.5 Algorithm Design

In Algorithm 1,all the willing blockchain users can be viewed as miner candidates and independently determine the resource demands of communication bandwidth,computation workload,and caching space.The edge computing server updates the floating unit prices according to each miner candidate’s demands until reaching the Stackelberg equilibrium.After specifying the demand and pricing,all the miner candidates give the bidding prices according to the estimated number of computing resources to be consumed.Afterward,the winning miners are selected in a greedy way based on the social welfare contribution.In order to constitute the miner network,the winning miners need to pay for the communication,computing,and caching services,and utilize the rent/self-resources to execute the mining process.Once the mined block is verified,the winners can share the rewards as (4).The computation complexity of Algorithm 1 is at mostO(MI+M2),whereIis the total iteration number.

III.SIMULATIONS

According to [12] and [18],the well-known Monte Carlo simulation is implemented for evaluating the performance of the proposal,where MATLAB R2016a is used to run the simulations on a WIN7 desktop computer with quad-core CPU(Intel i5-7400)and 8-GB RAM.Assume that the coverage radius of each edge computing server is 150m,and the density of the server is set at 10-4/m2.In each Monte Carlo simulation loop,all users are randomly distributed within the system,and the transaction number,the locally available computation ability,and the locally available cache size of each user are all evenly distributed over a reasonable range as summarized in Table I.After several loops,the average value is calculated to reduce the randomness effects.In addition,the wireless channels between each miner and its nearby server suffer independent and identically distributed Rayleigh fading with mean 1.The path loss constant is assumed to be 1[21],and the path loss exponent is set as 4.The values of key parameters are summarized in Table 1.

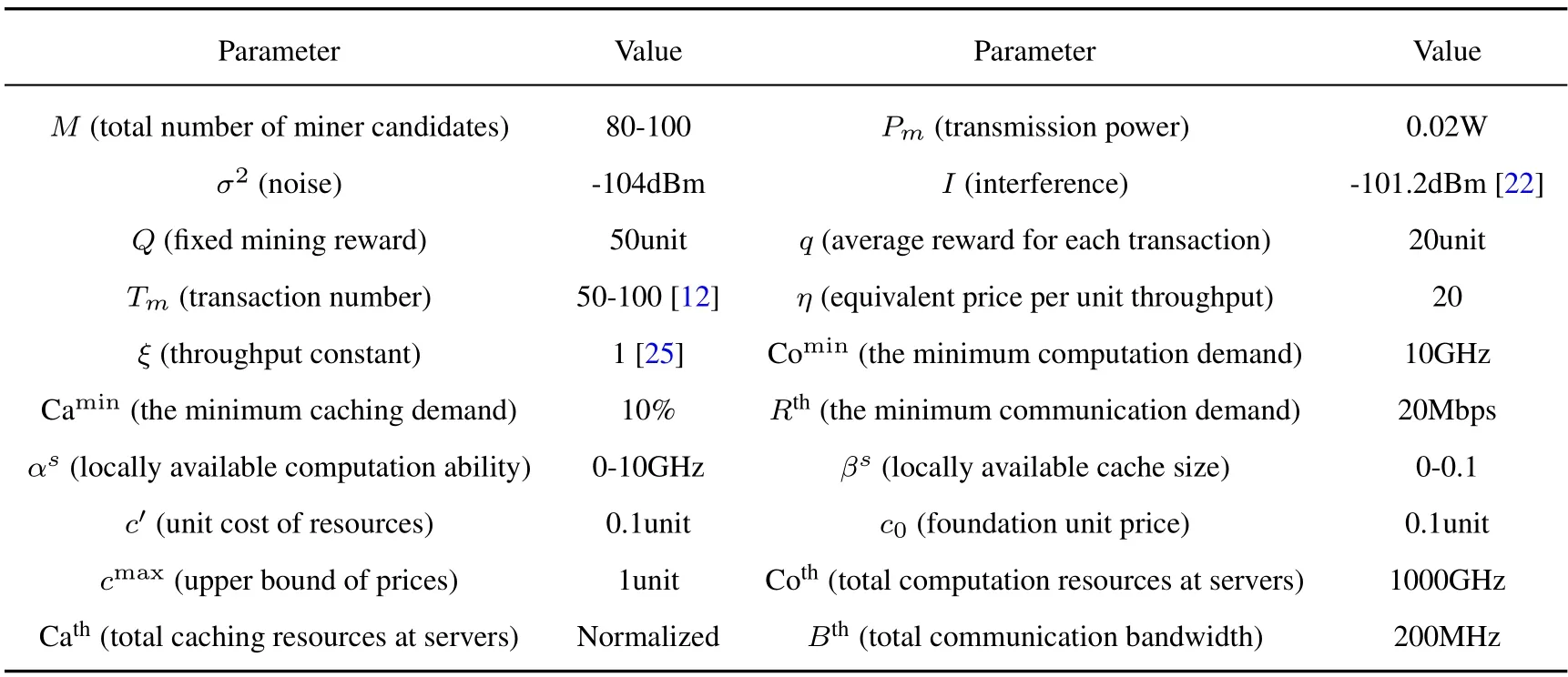
Table 1. System parameters.

We compare the proposal with the following schemes:

· Miner selection: This compared scheme can be viewed as the conservative scheme,where we assume that the winners always purchase a certain amount of the resources[12].

· Computation offloading: All the candidates compete without using their self-computing resources,i.e.,=0,∀m ∈M[13].

· Local computing: All the candidates compete only with their self-computing resources,i.e.,=0,∀m ∈M.

Figure 2 illustrates the performance comparison of different schemes.From Figure 2,we have the following conclusions:

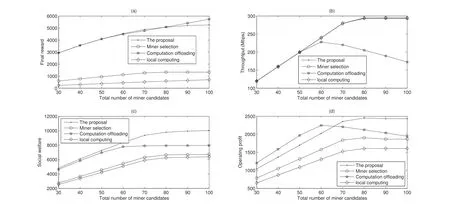
Figure 2. Performance comparison.

First,for the proposal,with the increment of the total number of miner candidates,the final reward,throughput,social welfare,and operating profit of servers show an increasing trend.Since the resources of the system are limited,increasing the number of candidates will not increase the number of winners when the candidate number is large;thus the curves all eventually converge.

Second,the proposal allows more flexible scheduling of resources in general so that it is superior to other schemes.According to the simulation results,compared with the scheme of miner selection,the proposal achieves around 280.07%,47.24%,and 27.96% improvements in terms of the final reward,social welfare,and operating profit,respectively.Compared with the scheme of local computing,the scheme of miner selection can quantitatively schedule computing resources and enhance system performance.Therefore,compared with the scheme of local computing,the proposal achieves around 647.79%,56.47%,and 51.30%improvements in terms of the final reward,social welfare,and operating profit,respectively.

Third,there exists a particular case,i.e.,the scheme of computation offloading.In this compared scheme,the local computing resource is assumed to be zero,which increases the rent-computing resource demands.With the increment of the total number of miner candidates,each of them has a higher standard of computing resources in order to strengthen competitiveness.Therefore,after the miner competition,the scheme of computation offloading may bring an enhanced final reward as shown in Figure 2(a).However,considered that the leasable resources owned by the system are limited,the number of winners in the scheme of computation offloading becomes less than the other schemes.Therefore,one can observe that the throughput begins to decrease when the number of miner candidates increases to a certain number in Figure 2(b).Note that the purpose of miner competition in this paper is to maximize social welfare instead of the final reward.Even though the final reward of this compared scheme may be larger than that of the proposal when the total number of miner candidates is large,its social welfare is still less than the proposal as shown in Figure 2(c).From Figure 2(d),the total profit of the edge computing server is larger than that of the proposal when the number of miner candidates is small.This is because the scheme of computation offloading needs to rent more computing resources,which increases the operating profit.As the number of candidates continues to increase,the number of selected miners is decreased as we discussed before,and the operating profit becomes reduced at the same time.Taking 100 miner candidates as an example,according to the simulation results,the final reward of the proposal is degraded by 8.21%.However,the throughput,social welfare,and operating profit of the proposal are increased by 69.97%,26.08%,and 24.90%,respec-tively.Taking 50 miner candidates as an example,according to the simulation results,the operating profit of the proposal is degraded by 13.88%.However,the final reward and throughput remain the same,and the social welfare of the proposal is increased by 4.32%.

Figure 3 illustrates the impact of the resource number and the minimum demand on system performance.In Figure 3,increasing the number of supplying resources or decreasing the minimum requirement will expand the feasible area of the optimization problem,thus enhancing social welfare and the total operating profit.In Figure 3(a) and 3(b),the lower value of Cominshows a faster rate of convergence.This is because that the lower value of Comindecreases the total requirement of the computation resource so that it increases the probability that the miner is selected and quickly reaches the limitation of the communication resource.According to the simulation results,taking Comin=5GHz as an example,when the percentage of supplying computing resources is increased from 80% to 100%,the social welfare is unchanged,and the operating profit is increased by 0.14% only.In Figure 3(c) and 3(d),taking Camin=0.05 as an example,the social welfare and operating profit are both unchanged with the increment in the percentage of supplying caching resources.The faster convergence of the curves here indicates that the constraints of the total computing resource limitation have more influence on the system than the constraints of the total caching resource limitation due to the parameter settings.

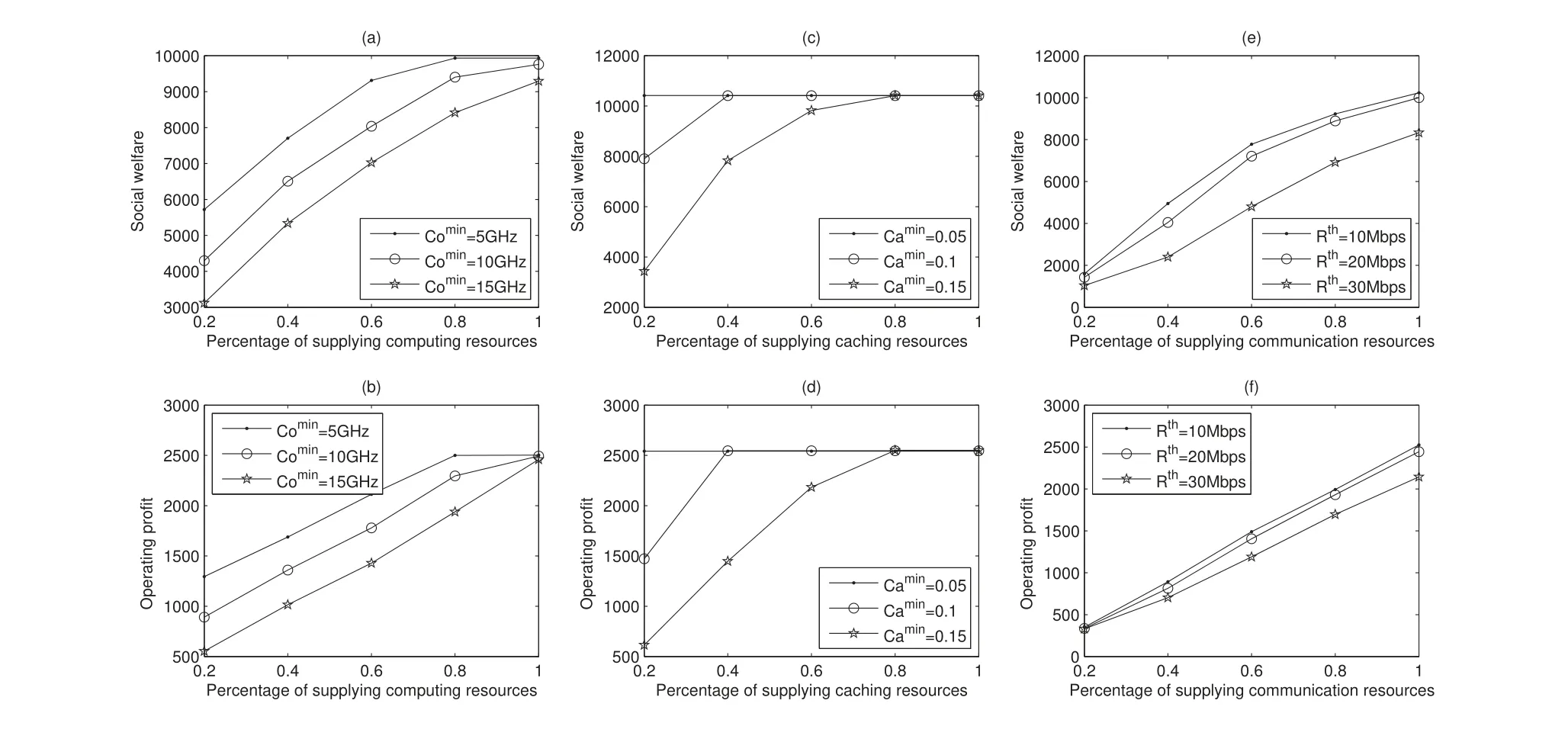
Figure 3. The impact of the resource number and the minimum demand on system performance.

IV.CONCLUSION

This paper presented a business ecosystem based on edge computing technology for blockchain users.Based on the business ecosystem,resource trading and miner competition were exploited to support the mining process in the proposed ecosystem.Simulation results demonstrated the advantages of the proposal compared with other schemes.This paper simplifies the communication scenario by analyzing the average spectrum efficiency of each miner candidate.In future work,we will design new schemes for a more efficient and practical blockchain system.

ACKNOWLEDGEMENT

This work was supported by National Natural Science Foundation of China (No.62271368,No.62201421),National Natural Science Foundation of Shaanxi Province (No.2021JQ-206),Guangdong Basic and Applied Basic Research Foundation (No.2020A1515110084),and China Postdoctoral Science Foundation (No.2018M640960,No.2019T120879).