Privacy-Preserving Deep Learning on Big Data in Cloud

Yongkai Fan ,Wanyu Zhang ,Jianrong Bai ,Xia Lei,* ,Kuanching Li

1 State Key Laboratory of Media Convergence and Communication,Communication University of China,Beijing 100024,China

2 Industrial and Commercial Bank of China Zhuhai Branch,Zhuhai 519000,China

3 Dept.of Computer Science and Information Engineering,Providence University,Taichung 43301,China

*The corresponding author,email: leixia2008530059@163.com

Abstract: In the analysis of big data,deep learning is a crucial technique.Big data analysis tasks are typically carried out on the cloud since it offers strong computer capabilities and storage areas.Nevertheless,there is a contradiction between the open nature of the cloud and the demand that data owners maintain their privacy.To use cloud resources for privacy-preserving data training,a viable method must be found.A privacy-preserving deep learning model (PPDLM) is suggested in this research to address this preserving issue.To preserve data privacy,we first encrypted the data using homomorphic encryption (HE) approach.Moreover,the deep learning algorithm’s activation function–the sigmoid function–uses the least-squares method to process nonaddition and non-multiplication operations that are not allowed by homomorphic.Finally,experimental results show that PPDLM has a significant effect on the protection of data privacy information.Compared with Non-Privacy Preserving Deep Learning Model(NPPDLM),PPDLM has higher computational efficiency.

Keywords: big data;cloud computing;deep learning;homomorphic encryption;privacy-preserving

I.INTRODUCTION

Big data analysis has made extensive use of cloud computing [1,2].The cloud can offer virtually limitless computing power to serve large computing demands and can accommodate the storage space needed for big data processing[3–5].As a result,using the cloud and moving data analysis from a traditional method to the cloud is crucial for big data analysis.Moreover,data owners are not constrained by the existing computational resources but can make use of the enormous resources.Despite these benefits,cloud computing’s openness makes it unsuitable for privacyrelated data processing,which often incorporates and manages sensitive information but is not limited to demographic,health,and financial data.With the evergrowing demand for computing resources,it seems reasonable that find a privacy-preserving-based big data analysis scheme in the cloud[6–9].

Generally,the data is encrypted to ensure privacy,though the use of general encryption methods reduces the data owner’s control over the data.For instance,deep learning methods cannot be used to directly train on encrypted data.The risk of data privacy leaks cannot be completely eliminated if the cloud is capable of holding the decryption key in-house.Big data analysis cannot be performed on the ciphertext appropriately if the data owner does not give the cloud the decryption key.The difficulty in such a situation is how to maintain data owner controllability while maintaining data privacy.

Deep learning,one of the key artificial intelligence techniques,mimics the human brain’s neural network to understand data.Deep learning can give computers equal intelligence and limitless development potential.Also,it represents the cutting edge of contemporary big data processing and analysis and is a crucial instrument in big data research.Therefore,this paper chooses deep learning as a theme based on cloud privacy-preserving.

This paper suggests a Privacy-Preserving Deep Learning Model to address the requirements of privacy-preserving and latent potential of deep learning (PPDLM).Homomorphic Encryption (HE)method is used for data encrypted before data can be uploaded to the cloud for the preservation of privacy consideration,as it allows direct operation on ciphertext without altering the controllability of the data.Also,the majority of processes are shifted to the cloud to improve processing efficiency.The primary attributes of PPDLM are computational effectiveness and data privacy protection are traded off.PPDLM divides data processing into two sections:the encryption portion is kept on the local side for privacy,while the heavy computational work is loaded in the cloud side for efficiency.

The rest of this paper is structured as follows.The related work is discussed in Section II.While Section IV details the PPDLM based HE,Section III offers the necessary background information for PPDLM.Based on the findings of the experiments,Section V shows the effectiveness of PPDLM.PPDLM is thoroughly discussed in Section VI.Section VII brings this paper to a close.

II.RELATED WORKS

There are many privacy-preserving algorithms combined with machine learning,and most of them are used to implement data privacy preserving during data mining.Logistic regression [10],neural networks[11],decision trees[12],k-means clustering[13],and Bayesian [14] are only a few of the machine learning techniques used.Some of these privacy-preserving machine learning algorithms encrypt data to achieve privacy[15,16],while others introduce noise[17,18]to achieve privacy.

The suggested PPDLM achieves privacy preservation via data encryption,which can safeguard data privacy while utilizing the cloud’s prevailing processing capacity.There are numerous neural network-related privacy-preserving algorithms.For instance,M.Abadi et al.[17] created a technique using deep learning and differential privacy to prevent the leakage of the training dataset’s private data.In addition,J.Yuan et al.[19] suggested a privacy-preserving technique that uses multi-party security computation to make sure that all participants learn together but keep each other’s data details a secret.A collision-free double cloud system is used in another privacy-preserving neural network technique investigated by M.Baryalai et al.[20] in an effort to reduce the significant overhead of the HE technology.The privacy-preserving neural network was also mentioned by A.Bansal et al.in[21].Yet,under their plan,the assumption that the data sets are distributed equally among participants serves as the foundation for privacy protection.Despite there appearing to be a difference between the study in this work and the approximation approach of the activation function,the privacy-preserving deep learning strategy proposed by Q.Zhang et al.[22]is identical to that in this paper aside from the aforementioned algorithms.P.Li et al.[23]provided their concept for how to create a multi-key complete HE scheme while taking the security of data encrypted with multiple keys into consideration.A deep learning method that also protects privacy was proposed by L.T.Phong et al.[24].In particular,it does not reveal participant data to the server and permits numerous participants to train all data sets on the neural network.

The primary distinction between the suggested method and the ones mentioned above is that data calculations are carried out in the cloud,utilizing the cloud’s preeminent processing capacity while ensuring that data privacy is maintained.Also,the leastsquares method used in this study to approximate the activation function differs from other methods in a number of ways.

III.PRELIMINARIES

3.1 Deep Learning

Artificial neural networks are the foundation of deep learning.The majority of speech and picture recognition systems are now built using deep learning technology.Deep learning has a hidden layer in addition to the input and output layers.As implied by the name,the output layer produces abstract responses produced by neural network models,whereas the input layer comprises standardized input data.For deep learning,the hidden layer is essential.In terms of model training,which typically uses a BP approach,the hidden layer might have multiple layers.The deep learning algorithm BP,which is based on gradient descent,is the most effective for building deep learning models.The forward propagation phase and the BP process make up the bulk of the BP algorithm’s learning process.(The training values are provided to the network during the forward propagation phase in order to obtain the excitation response.(2)To determine the response error of the hidden layer and the output layer,the excitation response and the target output are compared in the BP process.

Figure 1 depicts the deep learning technique applied in the PPDLM.The network operates as follows:given a sample as input,the feature vector of the sample is retrieved,together with the input value for each sensor according to the weight vector.The output of each sensor is then calculated using the Sigmoid function,and the output is then utilized as the input of the sensors of the following layer,and so on until the output layer.

The specific operations are as follows:

1.Initialize the ownership value randomly.

2.Perform the following steps on each input example:

(a) Calculate to obtain the output of each unit in the output layer.Then the error term of each cell of each layer is calculated reversely from the output layer.

(b) Calculate its error term for each element k of the output layer:

(c) For each hidden unit h in the network,calculate its error term:

where outputs represent a set of output layer nodes.

(d) Update each weight:

wherexjimeans the input from nodeito nodej,andwjiis the corresponding weight.

3.2 Full Homomorphic Encryption

When performing identical operations on the ciphertext using full homomorphic (FHE) [25],the operations only involve addition and multiplication.FHE typically uses four algorithms:

1.The key generation algorithm: It is used to generate the the private keyFH.skand the public keyFH.pk.The input is the security parameterηThe entire process can be expressed asFH.KeyGen(FH.η)→(FH.pk,FH.sk).

2.The encryption algorithm is used to encrypt data.The inputs are plaintextFH.ptand public keyFH.pk,the output result is ciphertextFH.ct.The whole process can be expressed as:FH.Encryption(FH.pt,FH.pk)→(FH.ct).

3.The decryption algorithm is used to decrypt the encrypted data.The inputs areFH.skandFH.ct,and the output isFH.pt.The entire process can be expressed as:FH.Decryption(FH.ct,FH.sk)→(FH.pt).

4.The ciphertext is computed using the evaluation procedure.Its inputs areFH.ctandFH.f,whereFH.frepresents the operation function to be performed.The output is the result of the operationFH.op.The entire process can be expressed as:FH.evaluate(FH.f)→(FH.op).

FHE can enable both addition and multiplication operations simultaneously,which are referred to as addictive homomorphism and multiplicative homomorphism,respectively,in the arithmetic world.The computation of these two procedures in FHE is shown in Figure 2.

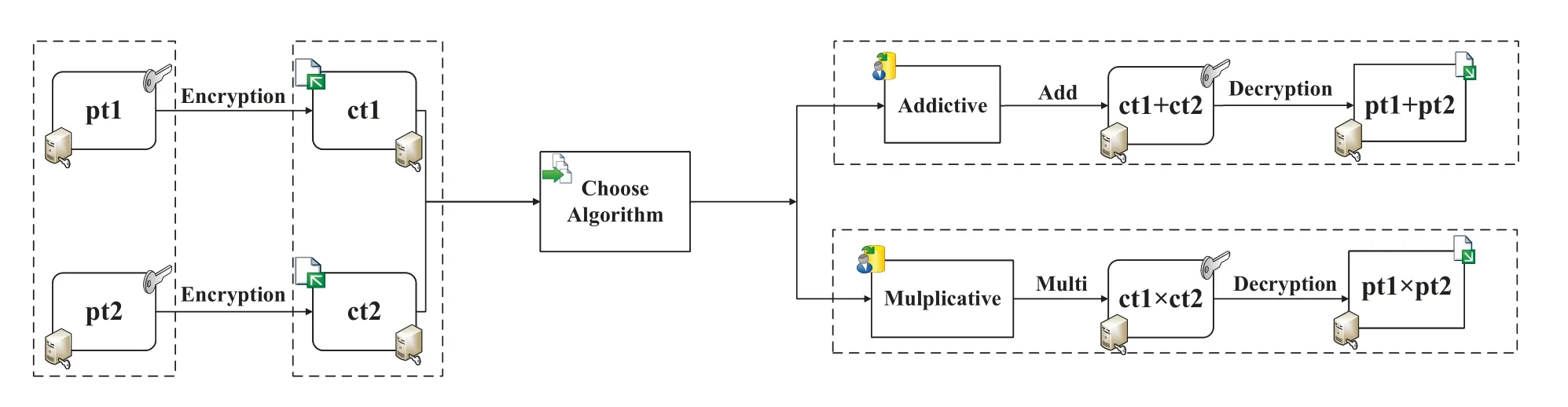
Figure 2. Homomorphic operations.

IV.SYSTEM MODEL

4.1 PPDLM Preview

To preserve the data privacy,PPDLM works as follows:1)encrypt training samples locally,approximate the activation function by the least-squares method;2)upload the ciphertext to the cloud to get the BP algorithm executed,3) send the trained result to the local side,and 4) get the computed ciphertext,decrypt to obtain the ultimate outcome locally.

4.2 Approximation of Activation Function

The activation function for deep learning,which incorporates exponential and divisional operations,is the sigmoid function.Unfortunately,the HE system only allows the operations of addition,subtraction,and multiplication.Because of this,the polynomialsum form of the Sigmoid function is simulated using the least-squares method.The polynomial-sum form operates directly on the ciphertext using only HE-supported operations.

In this paper,the matrix method of the least-squares method is used to fit the Sigmoid function.Under the circumstance that there are many target data pairs and the number of times of fitted function is relatively high,it is comparatively easy to use the matrix method for processing.Let the highest power of the polynomial in the fitting equation bem.Substitutingf(x)=a0+a1x1+a2x2+···+amxmintondata pairs:

A matrix represents the above equations,the vectorXis used to representxnm,the real data is represented by the vectorY,and the parameters are represented by the vectorA.The above equations can be expressed asXA=Y.The matrixXandYare generated according to the polynomial indexnand the sample pointmas follows:

Parameters can be obtained by performing derivation of the sum of squares of the errorG(x)=(XA-Y)T(XA-Y) with respect toA.By letting the derivative be zero,it yieldsXTXA=XTY,from which the parameterA=(XTX)-1XTYis obtained.

Compared with the algebraic method,the matrix method induces and derives the following formula from the complicated calculation of the derivation of data:

This paper fits the activation function through Algorithm 1:

The highest exponent of the fitting function we take isn=3and the number of sample pointsm=30,thus obtaining the final parameters: 0.000896,-0.00015,0.126549,0.499822.

The final fitting result is:

Figure 3 shows that the Sigmoid function is fitted with the least-squares method and Taylor theorem,respectively.As shown in Figure 3,the least-squares method is superior to Taylor theorem for fitting the Sigmoid function approximated by the least-squares method.

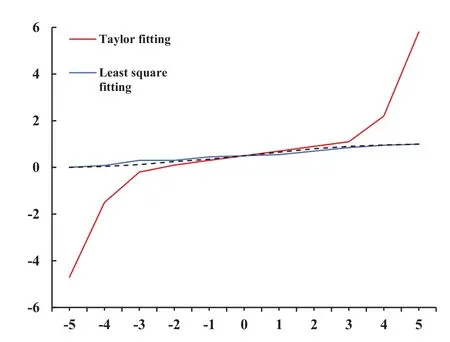
Figure 3. The approximation of the activation function.

4.3 Privacy-Preserving Deep Learning Algorithm

The detailed method is described as Algorithms 2,3,4 in order to display the entire PPDLM.The forward propagation stage and the BP stage are both parts of the BP algorithm.The calculation from the input layer to the hidden layer is the first step in the forward propagation stage.The weighted input sum of the neurons in the first hidden layer is calculated based on the value of the input layer,and the values of the other hidden layers are then calculated sequentially using the same approach.The value of the neurons in the output layer is computed based on the hidden layer’s value in the second step,which is the calculation from the hidden layer to the output layer.The particular procedure is displayed in Algorithm 2.

In the BP stage,firstly,the output layer error is calculated according to the target value,and the value of the output layer is calculated in the forward propagation stage,and then the error of the remaining layers is calculated in sequence.Secondly,weight and bias are calculated according to the error.In the stage of BP,the impulse term is added,which has the effect of increasing the search step size of converging faster,to a certain extent.On the other hand,multi-layer networks tend to cause the loss function to converge to the local minimum,but to some extent,the impulse term can go beyond some narrow local minimum to reach a smaller place.The specific process is shown in Algorithm 3.

Algorithm 4 details the whole process.After the BP algorithm being executed in the cloud,the local side decrypts the returned result from the cloud side.The data trained by the traditional deep learning algorithm(TDLA)is in the plaintext state.In contrast,the training data of PPDLM is in the ciphertext state.TDLA cannot identify the training data in the form of ciphertext,which is the first thing PPDLM needs to do.The adopted method is to use the FHE to encrypt the training data,and then convert all calculations in the BP algorithm for training.

V.IMPLEMENTATION

In this section,we evaluate the performance of PPDLM through experiments.In the local side,we conduct the experiment under such development enviroment: the operating system is CentOS 7.5,the language is C++,and the hardware configuration is a 2.60 GHz Intel 4-core processor and 3.7 GB memory.We simulate the cloud using a server which has a 3.40 GHz Intel Xeon processor and 31.3 GB memory.Section 5.1 provides an analysis of data sets and security.In Section 5.2,the experimental design and data processing are described.Section 5.3 introduces the results of the experiment.

5.1 Security Analysis

Two representative classification datasets,Pima and MNIST,are used in the experiment to assess the performance of PPDLM.Using specific diagnostic readings from the data set,the Pima[26]data set is used to determine whether a patient has diabetes.There are a total of 6,912 sample data in the Pima data collection.10,000 test samples and 60,000 training samples are part of the MNIST[27]data set.The total collection of data is made up of 250 different people’s handwritten numbers,of which 50% are the work of high school students and 50%are contributed by employees of the Census Bureau.This paper encrypts the data set,parameters and weights before training the data,and then uploads the encrypted data to the cloud to execute the back-propagation algorithm.From section 4.2 it can be known that for anyε ＞0,there exists a polynomialf(x)such that

wheres(x)is sigmoid function.Suppose thatPis the deep learning model with the activation functions(x),then on the domainD ⊂Rnthere is

Moreover,there exists a functionφ(x)such that

wherex={x1,x2,...,xn},Enc(x)={Enc(x1),Enc(x2),...,Enc(xn)},Dec(x)={Dec(x1),Dec(x2),...,Dec(xn)}.

On the other hand,the back-propagation algorithmβcan be operated over encrypted data to obtain the encrypted weights which can be decrypted to approximate the result learned on the plaintext.Let{ω1,ω2,...,ωN}be the weights learned fromβ,then for anyε ＞0 there is an algorithmβ′can obtain the weights{Enc(ω′1),Enc(ω′2),...,Enc(ω′N)}such that|ωi-ω′i|＜ε,1≤i ≤N.

The whole process is carried out in an encrypted state,does not involve the disclosure of original data and intermediate results,which can guarantee the privacy of the data.Therefore,PPDLM in this paper can completely ensure the security of the data.

5.2 Experimental Design

5.2.1 Experimental Composition

The experimental design is as follows:

1.Compare the running time between PPDLM and non-privacy privacy-preserving deep learning model (NPPDLM),wherein NPPDLM refers to placing all tasks in the cloud.The comparison highlights the performance of PPDLM clearly.

2.Compare the computing efficiency of PPDLM between the cloud and the local side.

3.Compare predication accuracy between PPDLM and traditional deep learning algorithm under the same iteration number,to show the influence of the Sigmoid function after the least-squares approximation and the non-processing Sigmoid function on the prediction accuracy.

5.2.2 Data Preprocessing

Before the experiment,in order to reduce the number of input neurons in the neural network and save the expense of time,the dimensionality of the MNIST data set is first reduced.The method adopted is as follows:each picture in the MNIST data set is 28*28 pixels,which is converted into a 28*28 number matrix.First,remove the numbers in the 3 circles around the 28*28 matrix and change it into the 22*22 matrix.Next,remove the numbers of three rows and three columns on the periphery of the 28*28 matrix and change it into a 22*22 matrix.Then,in this matrix,take one number every three numbers to form a new 8*8 matrix.Finally,the numbers in the 8*8 matrix are used as input data.

5.3 Findings

5.3.1 Encryption Time Before being uploaded to the cloud,training data,weights,and parameters must first be encrypted on the local side.The length of time required to encrypt Pima and MNIST,respectively,is shown in Figure 4.The encryption time of the weights of these two data sets is shown in Figure 5.As Figure 4 demonstrates,there is a strong correlation between the size of the data sets and the encryption time of the data.The execution time for the Pima training dataset is 93.12 minutes,whereas the MNIST training dataset (2000 bits of data) takes 4271.24 minutes,as shown in Figure 8.According to Figure 4,the Pima’s encryption time is 39.33 seconds,while the MNIST’s encryption time is 7687 seconds.When compared to the whole PPDLM execution time,the encryption time is such a little amount that it can be disregarded.Although encryption in the cloud takes less time than it does locally,this study opts to encrypt the data set and give more weight to the local side due to concerns about data privacy from the perspective of data owners.

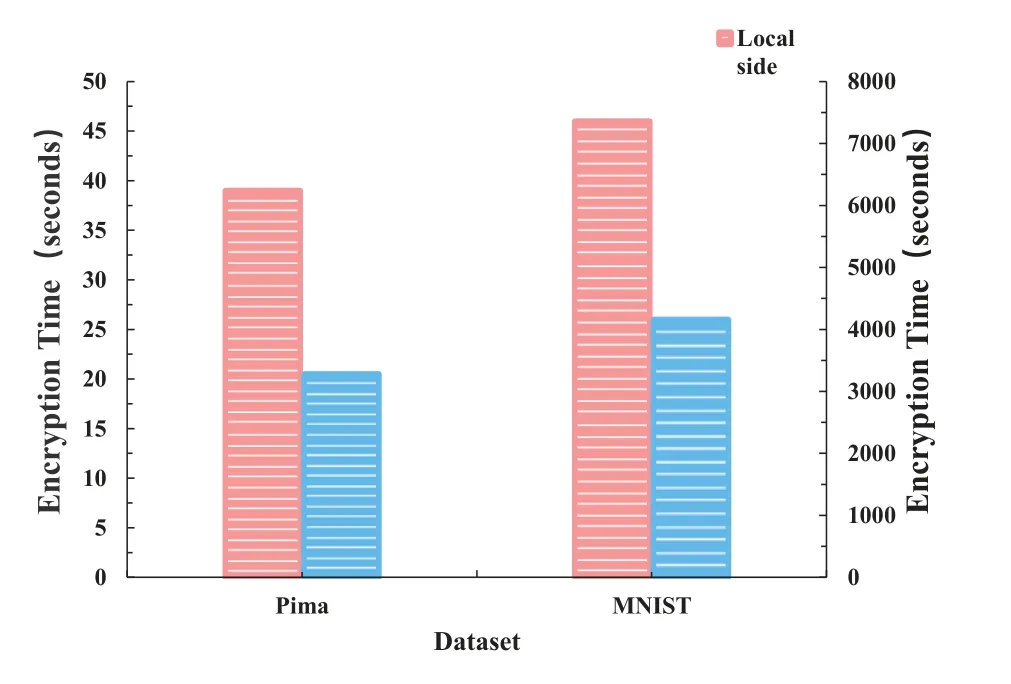
Figure 4. Encryption time of data sets.

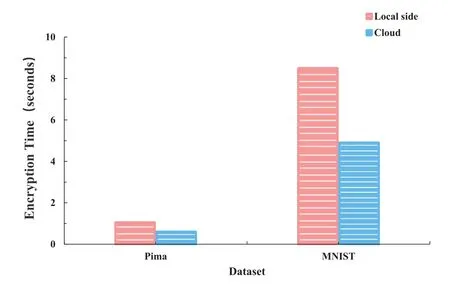
Figure 5. Encryption time of weights.

5.3.2 Computation Cost

In order to prove cloud computing’s advantages in processing big data and to evaluate the performance of PPDLM,two sets of comparative experiments are designed in this paper.The data set selected from these two sets of comparative experiments is MNIST,and iteration=1.The specific experiments are: 1)execution time of PPDLM in different data size.Figure 6 shows the experimental result.2)execution time of PPDLM and NPPDLM in different sizes.The experimental result is shown in Figure 7.

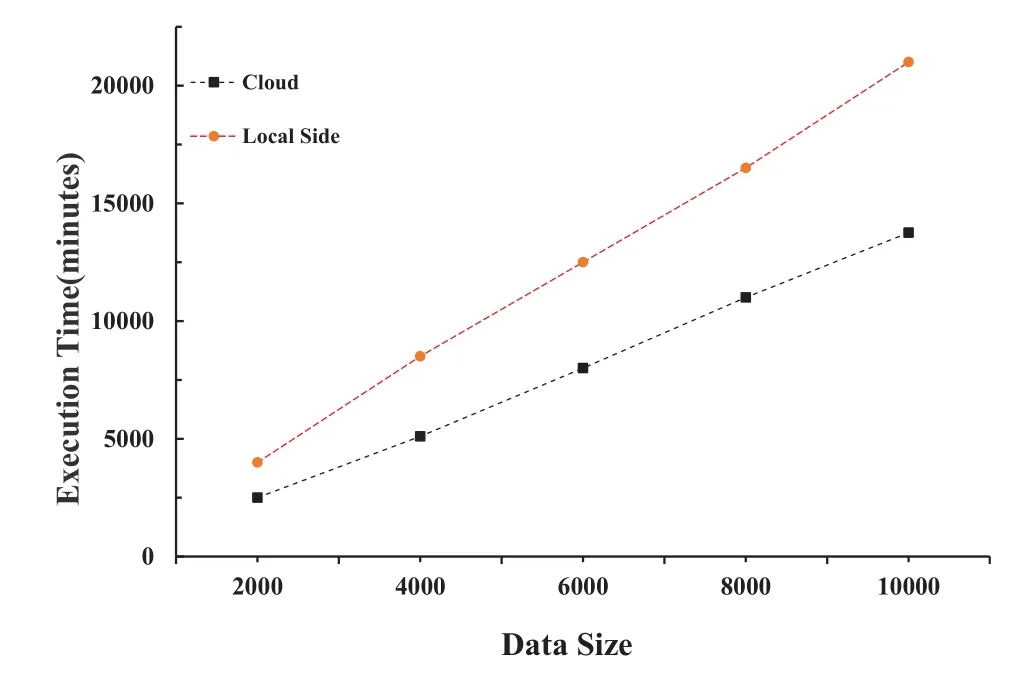
Figure 6. The execution time of MNIST running PPDLM under different data sizes of 2,000,4,000,6,000,8,000,and 10,000 respectively.

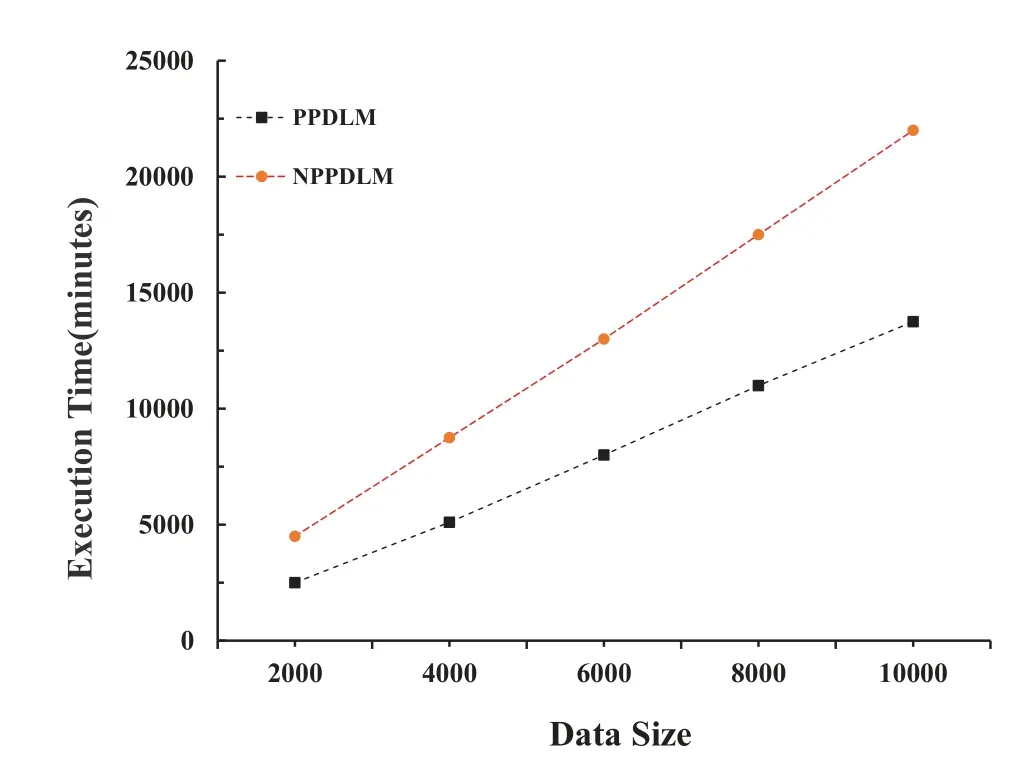
Figure 7. The execution time of MNIST running PPDLM and NPPDLM respectively under different data sizes of 2,000,4,000,6,000,8,000 and 10,000 in the cloud.

The comparison of PPLDM execution times is shown in Figure 6.The training time for a dataset of the same size is shorter on the cloud,as the graphic illustrates.Both the local side and the cloud have longer training times as data volume grows,but the growth rate of the cloud’s execution times is substantially slower.The testing findings unequivocally demonstrate that the cloud offers greater benefits than the local side.

As shown in Figure 7,time cost of PPDLM is shorter than that of NPPDLM for the same amount of data.As the amount of data increases,the training time of PPDLM and NPPDLM will both increase,but the training time of NPPDLM grows faster,which means that PPDLM has a better performance.

Figure 8 presents the execution time of Pima and MNIST respectively.As the figure illustrates,for a small batch of data,there is little difference(6.11 minutes) in the execution time between the two environments,i.e.the cloud and the local side.For large quantities of data,the impact of different operating environments on the execution time of PPDLM is still relatively significant.When training data of the same size,the running time of the MNIST data set in the local side is about 1.55 times as long as that in the cloud.As the amount of data increases,the difference between the running time will continue to increase.This shows that the cloud has significant advantages for training big data.

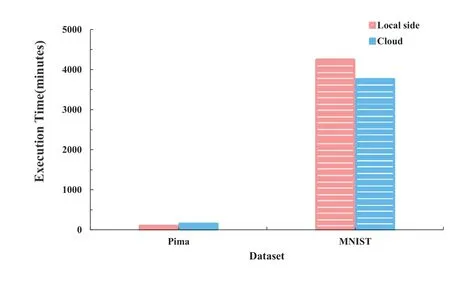
Figure 8. The comparsion of PPDLM execution time.

5.3.3 Accuracy Analysis

Figure 9 shows the variation of prediction accuracy of PPDLM and TDLA with different iterations.As can be seen from the Figure 9,the accuracy of PPDLM and TDLA all increase with the number of iterations.When iteration times increases to a certain degree,the increase in accuracy is not very obvious.The accuracy of PPDLM is lower than that of TDLA if both have the equal iterations.Using the least squares method to approximate the activation function will lead to a decrease in the accuracy of PPDLM.Although the prediction accuracy of PPDLM will be lower than that of TDLA,it is acceptable in feature learning related to big data[22].

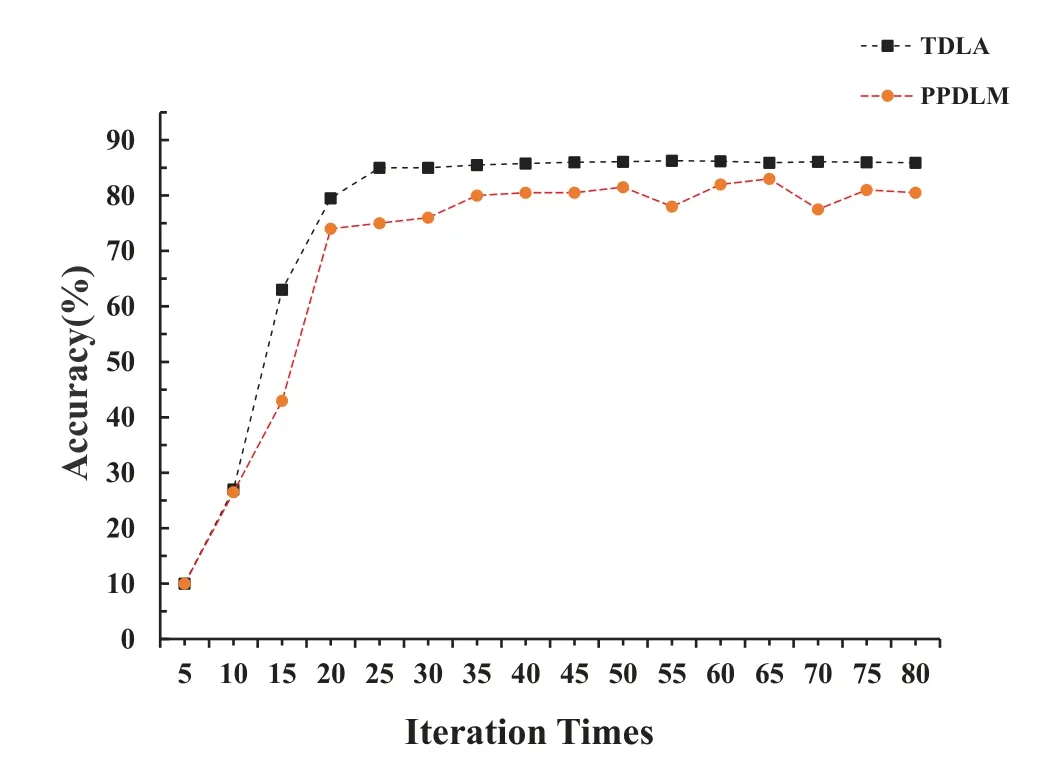
Figure 9. Predication accuracy with different iterations.

VI.DISCUSSION

The cloud’s powerful computing power makes the analysis and computation of big data more efficient and enables cloud users to experience convenient services.However,the data privacy of users in cloud computing cannot be guaranteed precisely,which is the main problem currently faced by cloud computing.To solve this problem,we propose PPDLM for using computing power in the cloud and keeping data privacy.In this paper,FHE is used to encrypt data,and it has strict requirements for data operations,and only supports addition and multiplication operations.The operations it does not support in the BP algorithm are approximated using the least-squares method.

The performance of PPDLM is evaluated through several experiments.To demonstrate the computing capabilities of the cloud,the same data set is employed.Then,in order to compare the algorithm performance of PPDLM and NPPDLM,they are each trained on the same data set on the cloud.To show how the approximation using the least-squares approach has an effect on the accuracy of the final output of PPDLM,the prediction accuracy of PPDLM and TDLA are compared under the same iteration.The least squares method is used to address the issue of the limited mathematical operations offered by HE,yet it still improves the precision of the final prediction findings.

VII.CONCLUSION

As artificial intelligence develops,big data plays a more significant role,so increasing the performance of its processing in a trusted way is particularly important.Cloud is such a place that can provide an efficient computing environment for Big Data processing.However,cloud computing has a limitation that it cannot preserve the privacy of data which is processed and stored in the cloud.For such,this paper proposes PPDLM,where data computation is offloaded to the cloud to improve computation efficiency,and FHE is used to encrypt data aiming to preserve data privacy.For privacy consideration,encryption/decryption does not performed in the cloud side,and data communication will incur additional time overhead,this overhead is acceptable compared with the running time of the entire PPDLM.

Experimental results demonstrate that:

1.PPDLM takes advantage of the strong computing power of the cloud to efficiently process big data while preserving privacy;

2.PPDLM seperates the operations into encryption/decryption and training,which leads to extra communication cost,however,the expense is not very high.In addition,the calculation efficiency can be improved by parallel processing of data by multiple servers;

3.The approximation of activation function will affect the prediction accuracy of PPDLM,but this effect is not very large and is completely acceptable in practical application.

As future work,other approximate processing methods need to be considered,as more efficient data encryption schemes need to be searched and identified to minimize the influence of approximate operations on the accuracy of the prediction result.Since the proposed PPDLM only involves the interaction between a single user and the cloud,the way how to ensure the data privacy of multiple users during the interaction with the cloud will also be investigated next.

ACKNOWLEDGEMENT

This work was partially supported by the Natural Science Foundation of Beijing Municipality (No.4222038),by Open Research Project of the State Key Laboratory of Media Convergence and Communication (Communication University of China),the National Key R&D Program of China(No.2021YFF0307600) and Fundamental Research Funds for the Central Universities.