Low Complexity Detection Algorithms Based on ADMIN for Massive MIMO

Shuchao Mi ,Jianyong Zhang,* ,Fengju Fan ,Baorui Yan ,Muguang Wang

1 Institute of Lightwave Technology,Beijing Jiaotong University,Beijing 100044,China

2 Key Lab of All Optical Network and Advanced Telecommunication of EMC,Beijing Jiaotong University,Beijing 100044,China

*The corresponding author,email: jyzhang@bjtu.edu.cn

Abstract: This paper proposes the alternating direction method of multipliers-based infinity-norm (ADMIN) with threshold (ADMIN-T) and with percentage (ADMIN-P) detection algorithms,which make full use of the distribution of the signal to interference plus noise ratio(SINR)for an uplink massive MIMO system.The ADMIN-T and ADMIN-P detection algorithms are improved visions of the ADMIN detection algorithm,in which an appropriate SINR threshold in the ADMIN-T detection algorithm and a certain percentage in the ADMIN-P detection algorithm are designed to reduce the overall computational complexity.The detected symbols are divided into two parts by the SINR threshold which is based on the cumulative probability density function(CDF)of SINR and a percentage,respectively.The symbols in higher SINR part are detected by MMSE.The interference of these symbols is then cancelled by successive interference cancellation(SIC).Afterwards the remaining symbols with low SINR are iteratively detected by ADMIN.The simulation results show that the ADMIIN-T and the ADMIN-P detection algorithms provide a significant performance gain compared with some recently proposed detection algorithms.In addition,the computational complexity of ADMIN-T and ADMIN-P are significantly reduced.Furthermore,in the case of same number of transceiver antennas,the proposed algorithms have a higher performance compared with the case of asymmetric transceiver antennas.

Keywords: ADMIN;low complexity detection algorithm;massive MIMO;MMSE;SINR

I.INTRODUCTION

The massive multi-input multi-output (MIMO) is a crucial technology of the fifth generation (5G) and even the sixth generation(6G)communication system[1–3].As the number of user terminals increases,the detection problem is more challenging in the uplink[4].This study focuses on the detection algorithms for uplink massive MIMO systems with comparable number of transmitting and receiving antennas.This scenario is important for multi-user(MU)MIMO systems at the base station side.There is no strict limitation on the relation between the numbers of transmitting and receiving antennas and one should avoid specifying a certain ratio in massive MIMO[5].On the other hand,as the number of the base station (BS) antennas increases,the random matrix theory demonstrates that the effects of uncorrelated noise and small-scale fading are diminished,and the number of supported users per cell becomes independent of the cell size.In addition,data detection in the uplink is among the most computationally expensive tasks at the BS side.The complexity of the detection process grows exponentially with the number of antennas at the BS.Thus,the detection problem becomes more challenging under the assumption that the ratio between the number of antennas in the BS and the number of users is small when dealing with MU-MIMO.Furthermore,as various types of mode diversity multiplexing(MDM)fibers with more than 100 spatial modes[6]have been studied on the feasibility of transmission,these detection algorithms developed for wireless communications have potential applications in MDM systems.

The massive MIMO system invokes a large number of antennas at the transmitter or receiver to achieve high spectral efficiency and high energy efficiency[1].However,the computational load of the maximum likelihood (ML) detection algorithm,which has theoretical optimal performance,exponentially increases with the increase of the number of antennas.To reduce the computational complexity of the ML detection algorithm,a sphere decoder (SD) [7,8] and several linear detection algorithms,such as zero forcing (ZF) and minimum mean square error (MMSE)[9,10],have been proposed,allowing to compromise between performance and complexity.However,in the case of high order modulation,the SD detection algorithm still has unbearably computational complexity.Because MMSE and ZF contain matrix inversion,they still have a high computation complexity in massive MIMO systems [11].Several detection algorithms based on approximate matrix inversion are proposed to avoid the complex operations:the Neumann Series (NS),Newton Iteration Method(NI),Gauss-Seidel(GS),Successive Over Relaxation(SOR),Conjugate gradients(CG),Coordinate descent(CD) [12],etc.A detection algorithm based on approximate message passing(AMP)is able to perform individually-optimal data detection given certain conditions on massive MIMO systems [13].Although these detection algorithms perform well compared to linear detection algorithms,there is a significant performance loss when the transmitter and receiver antennas are equal in number[14].Furthermore,the study in[15]demonstrated that there is a significant advantage for the MMSE detector in error performance,and this advantage is remarkable as the number of antennas increases,while it is much less as the difference between the transmitting and receiving antennas increases.However,ADMIN has a high performance when the system has comparable number of transmitting and receiving antennas [16–18].The relationship between transmitting and receiving antennas is not strictly required,and the massive MIMO system has important practical implications in the case of a small proportion of both [5,19],while only few researchers have studied this case.Moreover,this scenario is similar to the MDM in fiber communications,which has a potential application value.

SINR will affect the reliability of the MMSE detector,and a large SINR indicates that the interference and noise are relatively small[20,21].In fact,the distribution of post-processing SINR and the corresponding bit error rate (BER) performance of linear detection indicates that there are many symbols with high SINR,while directly using linear detection can provide a highly reliable solution.Directly using these high SINR symbols as part of the final detection result can reduce the complexity without affecting the detection performance[22,23].

To further decrease the computational complexity of ADMIN,the ADMIN-T and ADMIN-P detection algorithms for uplink massive MIMO systems are proposed.A threshold and an appropriate percentage are also designed to divide the detected symbols into two parts according to the distribution of SINR,respectively.The symbols with higher SINR are detected by MMSE instead of being iterated in ADMIN.The remaining lower SINR symbols are detected by ADMIN.The simulation results show that the proposed detection algorithms outperform MMSE,CG,and ADMIN and have lower complexity for massive MIMO systems which invoke a comparable number of transceiver antennas.

The remainder of this paper is organized as follow.The considered system model and ADMIN detection algorithm are detailed in Section II.The proposed detection schemes are introduced in Section III.In Section IV,the simulation results are presented to verify the performance of the proposed detection algorithms and computational complexity.Finally,Section V concludes the paper.

II.SYSTEM MODEL AND ADMIN DETECTION

2.1 System Model

A massive MIMO system model served withNTtransmitting antennas andNRreceiving antennas,such that(NR ≥ NT),is considered.The baseband signal model is given by

where y=[y1,...,yNR]∈CNR×1is the received signal vector which is corrupted by channel effects and noise,x=[x1,...,xNT]∈CNT×1is the transmitted symbols vector in which each entryxiis independently drawn from a complex constellation set C with zero mean and variance=ES/NT,the noise n∈CNR×1is a circularly symmetric complex white Gaussian noise vector with zero mean and variance=N0,and H∈CNR×NTis an independent and identically distributed(i.i.d.) Gaussian random vector with zero mean and unit variance.It is assumed that the channel state information is perfectly known at the receiver and the signal to noise ratio(SNR)is defined asSNR=ES/N0.

2.2 MMSE Detection

MMSE detection [5] is a linear detection algorithm,which minimizes the mean-square between the transmitted signal x and the estimated signal HHy .The signal is estimated according to the MMSE criterion as:

where G=HHH+ES/N0I denotes the equalizer matrix and=HHy represents the Matched equalization output.In contrast to the ZF detection,the MMSE detection depends on a reduced noise enhancement and requires a knowledge of the SNR.Therefore,the MMSE detection can achieve higher performance in the case of a large noise power [12].However,in massive MIMO systems the MMSE detection algorithm has an extremely higher computational complexity,which brings great challenge to its hardware implementation.

2.3 ADMIN Detection

This study first converts the ML problem into the constrained non-convex problem.The transmitted symbols are detected by minimizing the squared Euclidean distance between the received signal vector y and the hypothesized received signal Hx,while x is constrained to the modulation constellationONt,which can be expressed as

where the finite alphabetx ∈ONtcan be converted into the indicator functionas:

A constrained convex optimization problem can be written as

where z is the least-squares solution of the leastsquares and ˆx is the estimated transmitted symbol.The augmented Lagrangian for Eq.(5)is given by:

whereβ ＞0 is the penalty parameter andλis the scaled dual variable [18].ADMIN is a numerical method for efficiently solving convex optimization problems by decomposing the primal convex problems into smaller sub-problems [20].This problem is decomposed into three sub-problems that are repeated with iterations.The initial solution is=0,λ(0)=0,and the following equation can be used as the n-th iteration of ADMIN:

whereγis an appropriate step size.

The projection is given by:

whereqis closest toωwithin the box andCOis the convex polytope around the constellation set.Please note that the output of the first iteration in Eq.(7) is the solution of MMSE given by

whereβ=.

III.PROPOSED DETECTION SCHEME

3.1 ADMIN-T Detection Algorithm

According to Eq.(11),ADMIN uses the solution of MMSE detection as the starting point to iteratively find.It is shown in [21,22] that the estimated symbols with high SINR inare more reliable than those with low SINR.Thus,we conjectured that the symbols ofwith high SINR are not necessarily iterated in ADMIN.Based on this observation,these detected symbols can be divided into two sets A0and A1by a SINR threshold SINRth.The symbols in A0whose SINR is higher than SINRthare detected by MMSE,and the remaining symbols in A1with lower SINR are iteratively detected by ADMIN after SIC,which can cancelled the interference of A0.Note that A0={i:SINRi ≥SINRth}and A1={j:SINRj ＜SINRth}.

The SINR of thei-thantenna is given by

where Wi,iis the main diagonal element of W=(HHH+βI)-1HH=G-1HH.

LetF(x) be the cumulative probability density function(CDF)of SINR.The SINR threshold is then given by:

whereP0is a parameter uesd to balance the complexity and performance.

As shown in Eq.(13),F(x) should be determined and SINRthshould be calculated in of ine preprocessing.The detailed determination ofF(x)and SINRthis provided in the following section.

The proposed ADMIN-T detection algorithm with the preset threshold SINRthis summarized in Algorithm 1.In line 3 of Algorithm 1,the exact inverse R=G-1is computed to decrease the computational complexity using LDL decomposition [12] that can be performed during the preprocessing.The SINR is also calculated in the preprocessing of Algorithm 1 to lower the computational complexity.In the detection stage,the symbols are divided into two sets A0and A1by SINRthin line 8 of Algorithm 1.The symbols in set A0are directly output by MMSE and not iterated in ADMIN.The interference of these symbols is then canceled using SIC in line 13.After SIC,the remaining symbols in set A1are detected by ADMIN in lines 14-18.Note that WA0={wi:i ∈A0},wherewiis thei-throw of W,and HA0={hi:i ∈A0},wherehiis thei-thcolumn of H.

3.2 ADMIN-P Detection Algorithm

The ADMIN-T detection algorithm needs to collect a large number of SINR samples to calculate the SINRth,which should be determined in of ine preprocessing.There is another criterion that divides the symbols into two parts,without the need for preprocessing of ine.The ADMIN-T detection algorithm sets a threshold to divide the symbols into two parts.In addition,for different SNR values,the number of symbols with high SINR in A0will be different in each time.Based on this observation,an appropriate percentage can be chosen as the criterion.These detected symbols can be divided into two sets A0and A1by a certain percentageP.For example,ifP=0.3,the symbols in A0that are the top 30% of SINR are detected by MMSE,and the remaining symbols in A1are detected by ADMIN after SIC which can cancelled the interference of A0,where the SINR has been already sorted in descending order.Note that A0={SINRi:i ≤PNT}and A1={SINRj:j ＞PNT}.

The proposed ADMIN-P detection algorithm with percentagePis summarized in Algorithm 1.The preprocessing of the ADMIN-P detection algorithm is similar to that of the ADMIN-T detection algorithm.In the detection stage,the detected symbols are divided into two sets A0and A1by the preset percentagePin line 10 of Algorithm 1.The symbols in set A0with high SINR are detected by MMSE.After SIC in line 13 of Algorithm 1,the symbols in set A1are iteratively detected by ADMIN.

IV.SIMULATION RESULTS

4.1 SINR Distribution

Although the exact distribution of SINR for the MMSE MIMO system is investigated in [15] and it is available for the arbitrary number of antennas,it has extremely computational cost in the case of large number of antennas.In a wireless MIMO system,the Gamma or Generalized Gamma[24]distribution is usually used to approximate the distribution of SINR.In this work,more than 106SINR samples were collected for a 128×128 MIMO system with 16QAM to fit the probability density function(PDF)of SINR using Gamma and Generalized Gamma distribution.The PDF of SINR is shown in Figure 1.It can be seen that the Generalized Gamma distribution can perfectly fit the simulation.Therefore,in this paper,Generalized Gamma is used to approximate the PDF of SINR.According to the PDF curve of SINR,the CDF of SINR can be calculated and the SINRthof the ADMIN-T detection algorithm can be determined using Eq.(13).

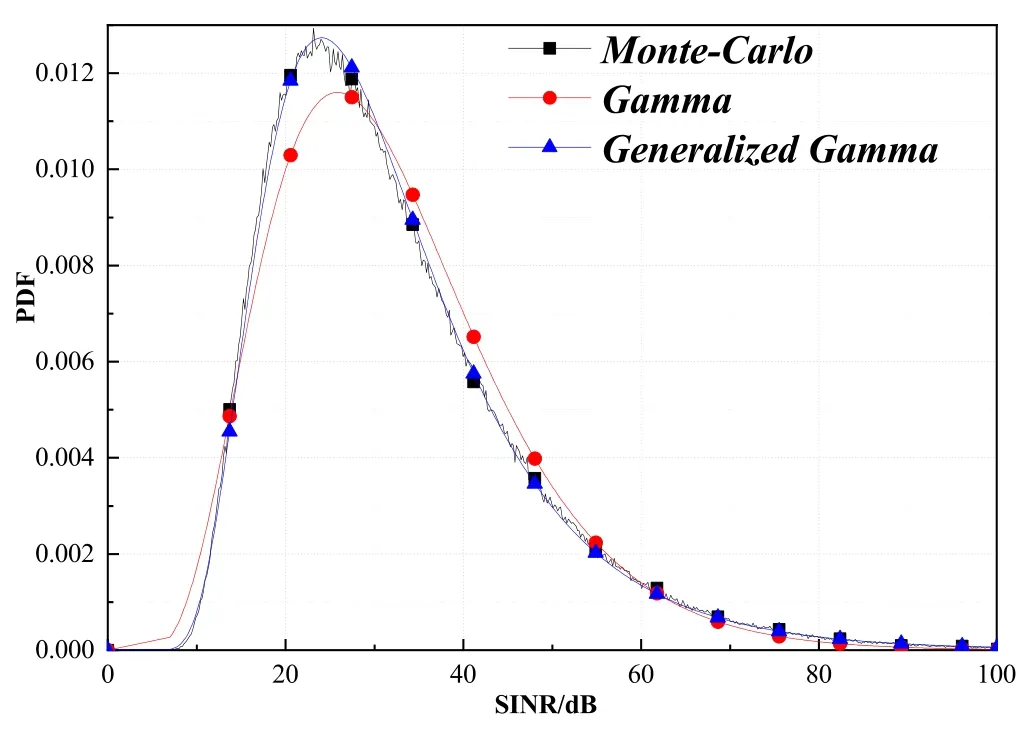
Figure 1. PDF of SINR for a 128×128 MIMO system with 16QAM at SNR=30dB.

4.2 Selection of the Percentage and SINR Threshold

Figure 2 shows the BER performance of the ADMINT detection algorithm with differentP0values for 64×64 with QPSK and 128×128 with 16QAM MIMO systems.It is shown in the figure that the BER performance of the ADMIN-T detection algorithm increases with the increase ofP0whenP0≤0.8 in both the 64×64 and 128×128 MIMO systems.It can also be seen that in the 128×128 MIMO system,the BER performance improvement is not significant when 0.8≤P0≤0.9.Furthermore,ifP0≥0.9,the BER performance decreases withP0.In particular,ifP0=1.0 which is equivalent to ADMIN,the ADMIN-T detection algorithm degenerates into the ADMIN detection algorithm.The BER performance of ADMIN-T starts to deteriorate compared with the otherP0in the 128×128 with 16QAM MIMO system.Similar results can be obtained from the 64×64 MIMO system with QPSK.However,the BER performance of ADMIN-T does not degenerate as much as in the 128×128 MIMO system with 16QAM whenP0=1.0.On the other hand,the BER performance improvement is not significant when 0.8≤P0≤0.9 and the BER performance starts to deteriorate whenP0≥0.9.Therefore,P0=0.8 is considered for all the simulations.

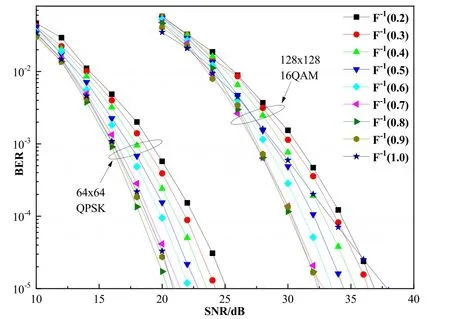
Figure 2. BER performance of the ADMIN-T detection algorithm with different P0 values for 64×64 and 128×128 MIMO systems with QPSK and 16QAM,respectively.

Figure 3 shows the BER performance of the ADMIN-P detection algorithm with differentPvalues ranging between 0.1 and 1.0 for 64×64 with QPSK and 128×128 with 16QAM MIMO systems,respectively.From Figure 3 we can see that the BER performance of ADMIN-P is improved with the decrease ofPin general.The 64×64 MIMO system with QPSK has a higher performance whenP=0.2.In addition,similar BER performance is reached whenP=0.2 andP=0.1 in the 128×128 MIMO system with 16QAM.In particular,ifP=1.0,which is the equivalent MMSE,the ADMIN-P detection algorithm degenerates into the MMSE detection algorithm that led to the lowest BER performance in both the 64×64 with QPSK and 128×128 with 16QAM MIMO systems.The simulation results show thatP=0.2 is the performance turning point,and it has a higher BER performance.Therefore,P=0.2 is considered for all the simulations.

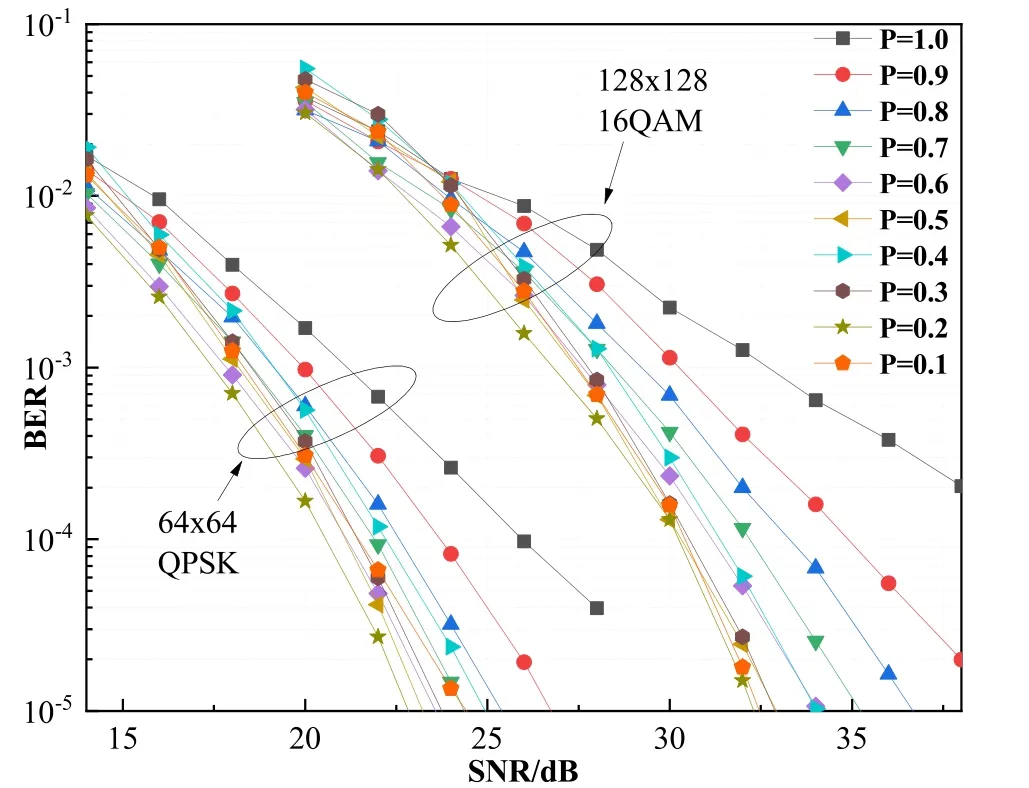
Figure 3. BER performance of the ADMIN-P detection algorithm with different P values for 64×64 with QPSK and 128×128 with 16QAM MIMO system,respectively.

4.3 BER Performance

The BER performance of ADMIN-T,ADMIN-P,ADMIN [18],CG [25],linear MMSE,and single input multiple output (SIMO) lower bound detection algorithms for massive MIMO systems with QPSK and 16QAM,are shown in Figure 4 and Figure 5,respectively.

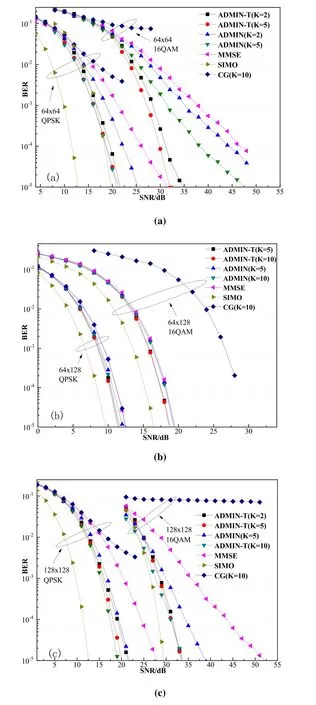
Figure 4. BER performance of the ADMIN-T,ADMIN,CG,and MMSE detection algorithms for massive MIMO(a)64×64,(b)64×128(one hundred twenty-eight BS antennas,64 users),(c)128×128 with QPSK and 16QAM.

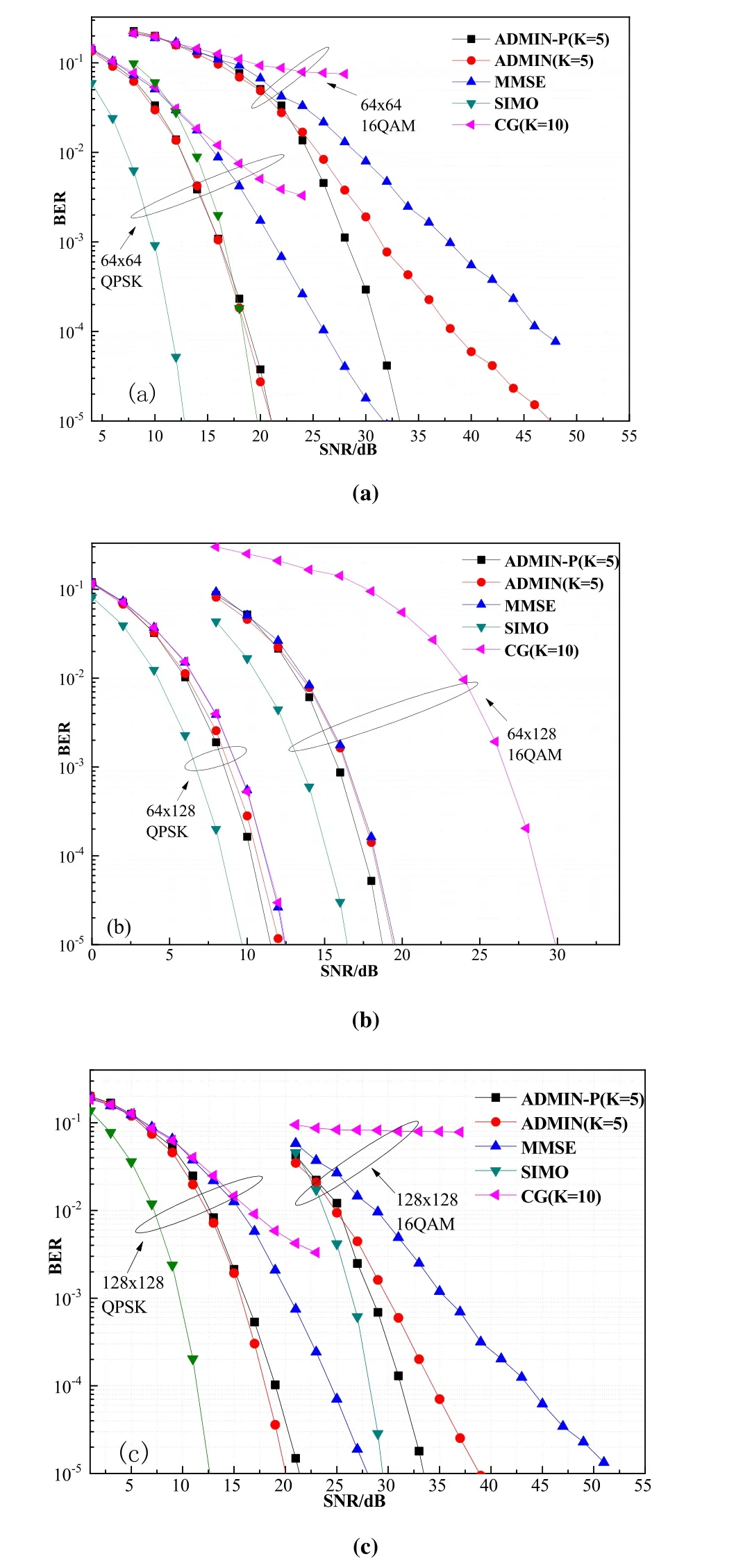
Figure 5. BER performance of the ADMIN-P,ADMIN,CG and MMSE detection algorithms for massive MIMO(a)64×64,(b)64×128(one hundred twenty-eight BS antennas,64 users),(c)128×128 with QPSK and 16QAM.

It can be seen from Figure 4 (a) that the performance of the ADMIN-T detection algorithm with K=2 is higher by 4dB compared with ADMIN with K=2 and 10dB compared with MMSE,for a 64×64 MIMO system with QPSK at a BER of 10-5,respectively.Although the two algorithms with K=5 perform similarly in this scenario,the ADMIN-T detection algorithm has a lower complexity.This will be discussed in the following section.In addition,the BER performance of the ADMIN-T detection algorithm is much higher than those of the ADMIN and MMSE detection algorithms in the same iterations for a 64×64 MIMO system with 16QAM.Moreover,the CG detection algorithm has a lower performance in this scenario.

Figure 4 (b) shows that the performance of the ADMIN-T detection algorithm is higher by almost 0.5dB better than ADMIN and MMSE for 64-user and 128 BS antennas system with 16QAM at a BER of 10-5.In addition,the CG detection algorithm has the lowest BER performance in this scenario.The performance of the ADMIN-T detection algorithm is 1dB higher than those of the MMSE and CG detection algorithms for the 64×128 MIMO system with QPSK at a BER of 10-5.The BER performance of the ADMIN-T detection algorithm is similar to that of the ADMIN detection algorithm for the 64×128 MIMO system with QPSK.However,the computational complexity of ADMIN-T is lower than that of ADMIN in spite of the similar BER performance.

Figure 4(c)shows that the ADMIN-T detection algorithm has approximately the same performance with K=2 and K=5,which is still greater by 5dB and 17dB than ADMIN with K=5 and MMSE for the 128×128 MIMO system with 16QAM at a BER of 10-5,respectively.The BER performance of the ADMIN-T detection algorithm converges at K=2.In addition,ADMIN needs more iterations to achieve the ADMINT performance.Moreover,the performance of the ADMIN-T detection algorithm is higher by almost 1.5dB than the ADMIN detection algorithm with K=5 for the 128×128 MIMO system with QPSK at a BER of 10-5.Although the performance of the ADMIN detection algorithm with K=10 is higher than that of ADMIN-T with K=5,the former requires more iterations,thus increasing the complexity.It can also be seen from Figure 4(a),(b)and(c)that,to a certain extent,the performance of the ADMIN-T detection algorithm in the case of asymmetric number of transceiver antennas is lower than that in the case of same number of transceiver antennas.On the other hand,when the modulation format is 16QAM,the BER performance of the ADMIN-T detection algorithm is superior in both the 64×64 and 128×128 MIMO systems.

It can also be seen from Figure 5 that the BER performance of the ADMIN-P detection algorithm is much higher than that of ADMIN,CG,and MMSE.Figure 5(a)shows that the ADMIN-P and ADMIN detection algorithms have similar performance with K=5 for the 64×64 MIMO system with QPSK.Furthermore,ADMIN-P outperforms MMSE and CG with a smaller number of iterations.However,the performance of the ADMIN-P detection algorithm with K=5 is almost 10dB higher than ADMIN with K=5 for the 64×64 MIMO system with 16QAM at a BER of 10-5.

Figure 5 (b) illustrates the BER performance for a 64-user and 128 BS antennas system with QPSK and 16QAM.For a lower order modulation (QPSK),ADMIN-P achieves a small performance gain over ADMIN,MMSE and CG detection algorithms.For a higher order modulation(16QAM),ADMIN-P outperforms ADMIN and MMSE.However,the CG detection algorithm performs worse than the other detection algorithms with K=10 iterations.ADMIN-P achieves approximately 1dB and 10dB gain compared with the ADMIN and CG detection algorithms,respectively.

Different detection algorithms are evaluated for a 128×128 MIMO system with QPSK and 16QAM(Figure 5 (c)).The CG detection algorithm fails to detect the symbols in this scenario.It can be seen that the ADMIN-P detection algorithm provides significant gain over ADMIN,MMSE,and CG for a 128×128 MIMO system with 16QAM.Although the performance of ADMIN-P detection algorithm with K=5 is lower than that of ADMIN for a 128×128 MIMO system with QPSK,the former has lower total computational complexity.Figure 5 (a),(b) and(c)illustrate that ADMIN-P achieves the highest BER performance and has higher advantage when the ratio of BS antennas to user ratio is low.In addition,ADMIN-P detection algorithm has the highest performance in both 64×64 and 128×128 MIMO systems when the modulation format is 16QAM.

Figure 6 shows a comparison between the BER performance of ADMIN-T and ADMIN-P detection algorithms for massive MIMO with various antenna configurations.The BER performance of ADMIN-T is higher than that of ADMIN-P,especially for the 64x64 MIMO system with 16QAM and 128x128 MIMO system with QPSK.However,in the 64x128 MIMO system,the two algorithms have almost the same performance.In general,the performance difference is more pronounced for smaller transmitting and receiving antenna ratios.These results confirm that the proposed ADMIN-T and ADMIN-P detection algorithms are suitable for comparable number of transmitting and receiving antennas.

Figure 6. BER performance comparison between ADMINT and ADMIN-P detection algorithms for massive MIMO(a)64×64,(b)64×128(one hundred twenty-eight BS antennas,64 users),(c)128×128 with QPSK and 16QAM.

4.4 Computational Complexity

In this section,the computational complexity of ADMIN-T and ADMIN-P detection algorithms is analyzed and compared with those of ADMIN,CG,and MMSE detection algorithms.Note that the number of multiplications required by the algorithms is considered as the measure of computational complexity[18].In addition,one complex number multiplication is equivalent to four real numbers multiplication.The MMSE detection requires a matrix inverse calculation,and therefore the total computational complexity is 4×((NT)3+NR(NT)2+NTNR).The total computational complexity of CG [26] detection algorithm is (K+1)(4U2+20U).According to[18],the complexity of ADMIN detection algorithm depends on the number of iterations,and it can be calculated asK(8NT2+12NT)+4NRNT.The computational complexity of ADMIN-P and ADMINT detection algorithm is mainly related to the selection ofPand SINRthobtained by simulations.For ADMIN-P,Prepresents the number of symbols with high SINR that is detected by MMSE.The computational complexity of ADMIN-P is then analyzed based on this concept.The number of complex-valued multiplications required for line 3 of Algorithm 1 is 2NT2.Thus,line 12 and 13 of Algorithm 1 require 3×((P ×NT)2+(P × NT)) complex multiplications.The number of complex-valued multiplications required for line 15 of Algorithm 1 is(1-P)× NTNR.The projection of line 16 of Algorithm 1 is negligible and the cost of line 17 requires(1-P)×NT.Therefore,the total computational com-plexity of ADMIN-P isK(8×((1-P)NT)2+12×(1-P)NT)+4×(1-P)NTNR+12×((P ×NT)2+(P ×NT)).

The computational complexity is similarly calculated for ADMIN-T.Assuming that there areNmsymbols with higher SINR according to SINRth,the total computational complexity of ADMIN-T is(NT -Nm)NR+12×((Nm)2+(Nm)).

Table 1 summarizes the computational complexities of ADMIN-P,ADMIN-T,ADMIN,CG,and MMSE detection algorithms for massive MIMO systems.

It is shown in the Table 1 that MMSE detection algorithm has the highest complexity among all the detection algorithms.That of ADMIN-T is slightly lower than that of ADMIN-P,and it is the lowest computational complexity.The computational complexity of ADMIN-T detection algorithm is 34.9% and 35.3%lower than that of ADMIN with K=2 and K=5 for a 64×64 MIMO system,respectively.The computational complexity of ADMIN-T detection algorithm is 47.5% and 46% lower than that of ADMIN with K=5 and K=10 for a 64×128 MIMO system,respectively.Although the BER performances of ADMIN with K=10 and ADMIN-T detection algorithms with K=5 are almost similar(Figure 4(c)),the complexity of ADMIN-T is still 66.3%lower than that of ADMIN for a 128×128 MIMO system.In addition,CG detection algorithm has similar or even less computational complexity than ADMIN detection algorithm.However,its BER performance is much lower than those of the other detection algorithms.

V.CONCLUSION

This paper proposed a reduced computational complexity version of the ADMIN-T and ADMIN-P detection algorithms for uplink massive MIMO systems.The proposed ADMIN-T and ADMIN-P detection algorithms avoid the calculation of the Gram matrix and matrix inversion.In addition,a preset percentage and threshold are designed to divide the algorithms into two parts according to the distribution of SINR.Appropriate detection algorithms are used for different parts.The simulation results show that the proposed ADMIN-T and ADMIN-P detection algorithms can improve the BER performance,and have a low computational complexity compared with MMSE,CG,and ADMIN.In addition,in the case of the same number of transceiver antennas,the proposed algorithms have an advantage over the number of asymmetric transceiver antennas.

In future work,the ADMIN-T and ADMIN-P detection algorithms will be used for precoding in the massive MIMO downlink.Computing the performance of ADMIN-T and ADMIN-P detection algorithm in the presence of channel estimation is also of our interest.Finally,data detections are suffering from severe performance loss or high computational complexity in real channel scenarios.Therefore,there is a significant room for data detections based on the deep learning approach.

ACKNOWLEDGEMENT

This work was supported in part by the National Natural Science Foundation of China(NSFC)under grant numbers 61671047,61775015 and U2006217.