非可微条件下全局隐函数存在性定理
罗春林, 武淑霞, 赵江林
(四川民族学院 理工学院, 四川 康定 626001)
0 引 言
全局隐函数定理在非线性分析、积分方程、物理、化学、控制论等领域都有非常重要的应用.经典的全局隐函数存在性定理如下[1]:
引理1如果函数F∶D=[a,b]×→满足条件:(i) 在D中处处连续;(ii) 处处有关于第二变量于y的偏导数存在常数m,M满足则方程F(x,y)=0在区间[a,b]上必有唯一的连续函数y=f(x)作为解:F(x,f(x))≡0,∀x∈[a,b].
在文献[2]中的定理1,将引理1的条件(i)减弱为“函数F(x,y)在D中关于第一变量x处处连续”而其它条件不变的情况下,证明了结论也成立.
在引理1和文献[2]的定理1中,都要求已知二元函数F(x,y)关于第二变量y偏导数存在.在定理学习和教学过程中,很自然提出将可微条件减弱为非可微条件时,结论是否成立.为此,通过引入强单调和Lipschitz连续两个概念,在非可微假设条件下,即,不要求F(x,y)关于y的偏导数存在,证明了一个全局隐函数存在性定理,从而将文献[1-2]的相关结论推广到非可微情形.
1 主要结论
为了得到新的定理,设E⊂,f∶E→,引入强单调和Lipschitz连续两个概念[3].
定义1函数f称为是α-强单调的,如果存在一个常数α>0,满足下面条件:
(f(x)-f(y))(x-y)≥α|x-y|2,x,y∈E.
定义2函数f称为是β-Lipschitz连续的,如果存在一个常数β>0,满足下面条件:
|f(x)-f(y)|≤β|x-y|,x,y∈E.
注1 容易验证,引理1中的函数F满足条件(ii)和(iii)时, 函数F关于第二变量y是m-强单调和M-Lipschitz连续的.事实上,由微分中值定理,对任意的(x,y1),(x,y2)∈D,存在θ∈(0,1)使得
由条件(ii)和(iii)可得
(F(x,y1)-F(x-y2))(y1-y2)≥m|y1-y2|2, |F(x,y1)-F(x-y2)|≤M|y1-y2|.
利用强单调和Lipschitz连续两概念得到如下新的全局隐函数存在定理.
定理1设函数F:[a,b]×→满足条件:(i) 在[a,b]关于第一变量x处处连续;(ii) 关于第二变量y是m-强单调的;(iii)关于第二变量是M-Lipschitz连续的,且m 注2 在定理1中的函数F关于第二变量满足m-强单调和M-Lipschitz连续时,不能保证F关于第二变量的可微性,即不能保证引理1中和条件(ii)和(iii)成立.例如:定义函数G(x,y)如下: 显然,G(x,y)在(x,0)处关于第二变量y的偏导数不存在,但是,容易验证关于第二变量是1-强单调和4-Lipschitz连续的.事实上,对任意的(x,y1),(x,y2)∈[1,2]×有 由上式可知 (G(x,y1)-G(x,y2))(y1-y2)≥|y1-y2|2, |G(x,y1)-G(x,y2)|≤4|y1-y2|. 在证明定理1的过程中,同样需要用到压缩映射和Banach压缩映射原理:从度量空间X到自身的映射T称为是压缩映射,如果d(Tx,Ty)≤αd(x,y),∀x,y∈X,其中常数α满足0<α<1;如果度量空间X是完备的,那么压缩映射T有且只有一个不动点. 定理1证明对任意固定的x0∈[a,b],在完备度量空间上定义映射T∶→: (1) 对任意的y1,y2∈,由F关于第二变量y的m-强单调性和M-Lipschitz连续性有 |T(x0,y1)-T(x0,y2)|≤θ|y1-y2|, (2) 因此,映射T:→是压缩映射,由Banach压缩映射原理,存在唯一的y0∈,使得 所以F(x0,y0)=0,定义f(x0)=y0,由x0∈[a,b]的任意性,就得到从[a,b]到的唯一函数y=f(x),满足F(x,f(x))=0,∀x∈[a,b]. 下证函数y=f(x),x∈[a,b]是连续的.对任意的x1,x2∈[a,b],由上面的证明可知,存在y1=f(x1),y2=f(x2),满足 F(x1,f(x1))=0,F(x2,f(x2))=0, (3) 并由(2)式可得 |T(x1,f(x1))-T(x1,f(x2))|≤θ|f(x1)-f(x2)|, (4) 由(3),(4)式和T的定义可得 所以 上式中,固定x2,让x1→x2,由F(x,y)关于第一变量x的连续性和F(x2,f(x2))=0可知 |f(x1)-f(x2)|→0,x1→x2. 所以y=f(x)在x2处连续,再由x2∈[a,b]的任意性,y=f(x)在[a,b]上连续. 本文通过引入强单调和Lipschitz连续两个概念,利用Banach压缩映射原理证明了在非可微条件下的一个全局隐函数存在性定理,由注1和注2可知,得到的定理1是引理1和文献[2]中定理1的真推广.更进一步,引导同学们思考,本文的全局隐函数定理条件是否还可以减弱?培养学生有一定的创新意识、创新思维和创新能力,是本科数学教学的教学目标之一.针对定理的教学,经常引导学生思考:当定理条件减弱一些的情况下,探讨定理的结论是否成立.本文针对全局隐函数推广过程,对本科数学的这一教学目的有一定作用. 致谢作者非常感谢审稿专家对本文提出的宝贵建议和意见.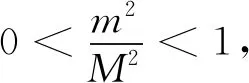
2 结 论

